† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61475196).
The interaction between C60 nanoparticles and biomembranes has been of great interest in researches over the past decades due to their novel applications as well as potential cytotoxicity. In this work, we study the deformation of the small unilamellar vesicles composed of dipalmitoylphosphatidylcholine (DPPC) lipid bilayers infiltrated with C60 nanoparticles of different molecular concentrations through coarse-grained molecular dynamics simulations. By employing the Helfrich spontaneous curvature model, the bending modulus and the spontaneous curvature of the vesicles with C60 nanoparticles of different concentrations are obtained according to the simulation data. The results show that the bending modulus and the spontaneous curvature of pure DPPC vesicle membranes are approximately 1.6 × 10−19 J and 1.4 nm−1, respectively. Both of them increase linearly approximately as the C60 concentration increases from 0 to 16.3%. The density profiles of vesicles, the order of lipid packing and the diffusion characteristics of DPPC and C60 are also investigated.
In the past decades, nanomaterials have been developed rapidly due to their remarkable physical and chemical characteristics and numerous potential applications in the biological and medical fields.[1–4] Among these nanomaterials, fullerenes, including functional C60, C60 derivatives and polymer/C60 composites, have attracted massive attention.[5,6] Those C60 nanomaterials exhibit crucial physicochemical properties like solubility in diverse solvents, redox properties, optic properties, etc.[5–7] Therefore, they are candidates for such hopeful biomedical applications as anti-oxidation, enzyme inhibition, antiviral activity, electron transfer and photodynamic therapy.[5–7] Despite a broad and fascinating prospect of C60 in biomedicine, they potentially lead to cytotoxicity.[8–10] Cases in point are studies about C60 causing oxidative damage to cell membranes,[11,12] changing the morphology of vascular endothelial cells,[13] inhibiting cell differentiation and suppressing cell proliferation.[14,15] Consequently, it is necessary to investigate the interaction between C60 and cells for biomedical applications.
Biomembranes play an indispensable role in many important functions of cells. Although biomembranes are complexes of various types of molecules, they all consist of a lipid bilayer serving as a backbone for membrane proteins and carbohydrates.[16,17] Usually, the bilayer containing only one kind of lipid molecules is employed as a simplified model in the study of biomembranes. Due to the amphipathic character of lipids, the lipid bilayer in water could assemble spontaneously into a unilamellar vesicle, which is employed as a simple model of cell in the literature.[18–21] In recent years, it has been found that vesicles could be taken as the nano-encapsulation agents for medicine.[22–24]
Investigating the mechanic effects of C60 on biomembranes (e.g., the alteration to rigidity) are vital for understanding its cytotoxicity and targeted drug delivery.[25–28] Zhang and co-workers concluded experimentally that C60 nanoparticles make human red blood cell membranes softer.[29] Drasler et al. reported a drop in the bending rigidity of POPC bilayers by the addition of 10% of C60.[30] Meanwhile, Skorkina et al. found that the aqueous solution with the C60 concentration of 0.1 mg/ml can increase the stiffness of the lymphocyte membrane by 41%.[31] In addition, Zhou et al. revealed that the incorporation of C60 with a molar concentration of 0.8% can increase Young’s modulus of gel phase lipid bilayers, but barely changes that of fluid phase bilayers.[32]
On the other hand, molecular dynamics (MD) simulations showed that C60 molecules are capable of translocating to the internal region of lipid bilayers spontaneously, affecting the structures and mechanic properties of plane membranes as well as inducing the dynamic interactions.[33–40] Wong-Ekkabut et al. carried out a simulation study on a plane lipid membrane and concluded that C60 with a concentration lower than 10% alters the elasticity of lipid bilayers, but is not enough to mechanically disrupt the membranes.[41] Recently, Xie et al. suggested that the initial aggregation state of C60 has an influence on the interactions between C60 and lipid bilayers: small C60 clusters expand the area and thickness of plane membranes while large ones decrease the membrane area by the protrusion of lipids.[42]
The shapes of closed vesicles are well described by the Helfrich spontaneous curvature model.[43] Accordingly, the elastic energy E of a closed vesicle is
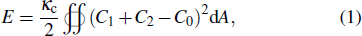
The bending modulus and the spontaneous curvature are critical parameters evaluating the elastic properties of lipid bilayers quantitatively. So far, there have been some researches on measuring the bending modulus of simple lipid bilayers through simulations or experiments. However, the obtained values are not consistent.[48–60] Moreover, few researches have determined the spontaneous curvature.[51,56] Venable et al. utilized the method of thermal fluctuations to calculate the bilayer bending modulus and the monolayer spontaneous curvature of pure lipid bilayers through MD simulations.[59] Nevertheless, they did not obtain the spontaneous curvature of bilayer directly.
In this work, we employ the Helfrich spontaneous curvature model to obtain the dependence of the bending modulus and the spontaneous curvature of dipalmitoylphosphatidylcholine (DPPC) lipid vesicles on the concentration of C60 nanoparticles through MD simulations. The results show that the infiltration of C60 nanoparticles into the vesicles increases the bending modulus and the spontaneous curvature linearly approximately. Furthermore, other structural and dynamic properties of the vesicles with C60 infiltration are studied to explain the elastic alteration.
The MD simulations were performed through Gromacs 5.1.1,[61–63] using the Martini coarse-grained (CG) force field.[64,65] The visual images were produced by VMD 1.9.3.[66] The Martini CG models of DPPC and C60 are shown in Fig.
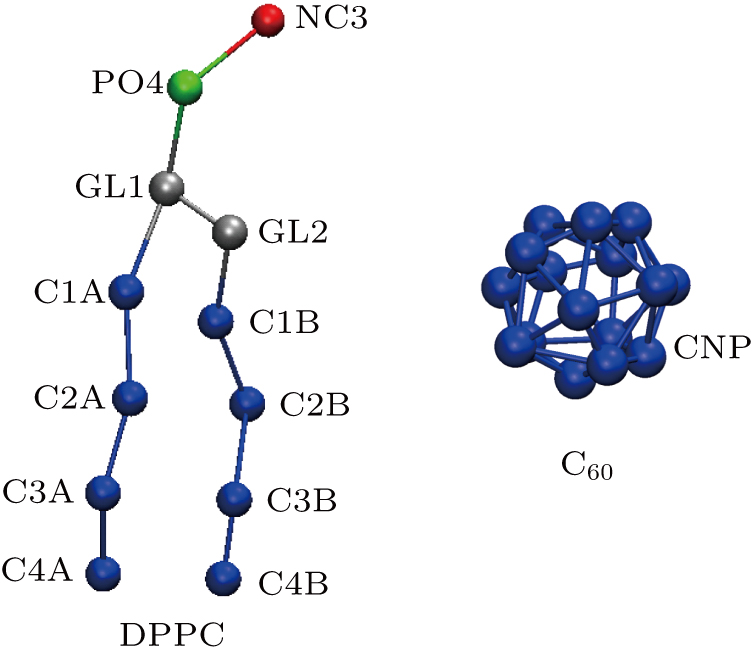 | Fig. 1. CG molecular representations of DPPC and C60. A DPPC molecule consists of 12 CG beads labeled by names and colors. A C60 molecule consists of 16 CNP CG beads. |
The lipid vesicle used in the current simulations was generated by Martini Vesicle Maker of CHARMM.[67,68] A lipid vesicle was placed in a cubic simulation box with a side length of 24.5 nm. Each simulation box contains 2637 DPPC molecules and 95252 CG water beads. The system was equilibrated at the temperature of 303 K and the isotropic pressure of 1.0 bar (ambient pressure p0).
The coordinate file of a single C60 molecule was extracted from the website of Martini force field (
For each of the equilibrated C60-vesicle systems, the dynamic simulations were performed applying a semi-isotropic pressure coupling in three-dimensional Cartesian rectangular coordinates. In this way, the components of the mechanic stress along x and y directions (horizontal direction) maintained ambient pressure, while the component along z direction (vertical direction) was assigned as 4.0, 8.0, 12.0, 16.0, and 20.0 bar, respectively. The constant pressure was implemented by the Berendsen scheme with a coupling constant of 5.0 ps. The temperature was constantly set at 303 K by the velocity-rescaling scheme with a coupling constant of 1.0 ps. Both the electrostatic cut-off and the van der Waals cut-off were at 1.1 nm. The time step of simulations was 30 fs.
The systems were regarded to achieve equilibrium when the side length of the system boxes remained stable relatively. Then the simulations were terminated. In our case, each simulation of the semi-isotropic pressure coupling was run for 300 ns.
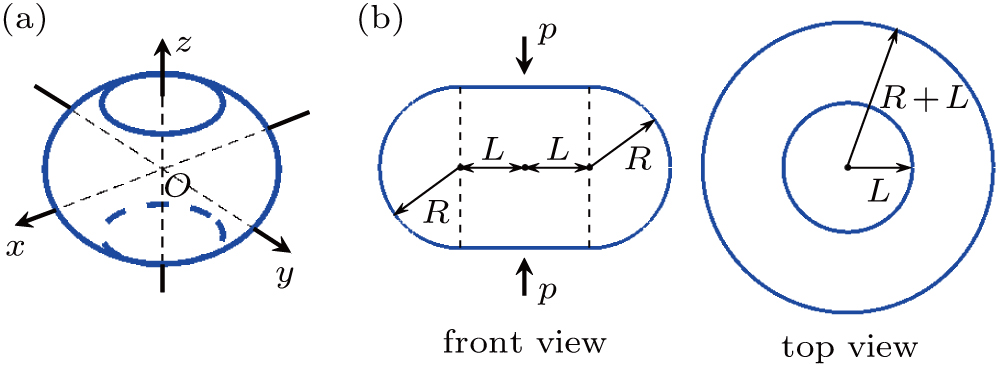
As a consequence of the vertical pressure, the initially spherical vesicle will deform. According to the simulations, the deformed vesicle can be abstracted into a geometry consisting of a rotationally symmetric side surface and two round planes at top and bottom, depicted in Fig.
At a constant temperature, the exchange of molecules between the membrane and the solution is negligible, and the membrane is hardly stretchable.[43] Thus, the area of the vesicle membrane during pressurization is assumed to be a constant. Accordingly, L is represented as a function of R,
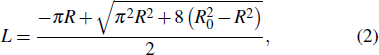
One can obtain the elastic energy of the vesicle based on the Helfrich spontaneous curvature model
On the other hand, one has

Using Eqs. (
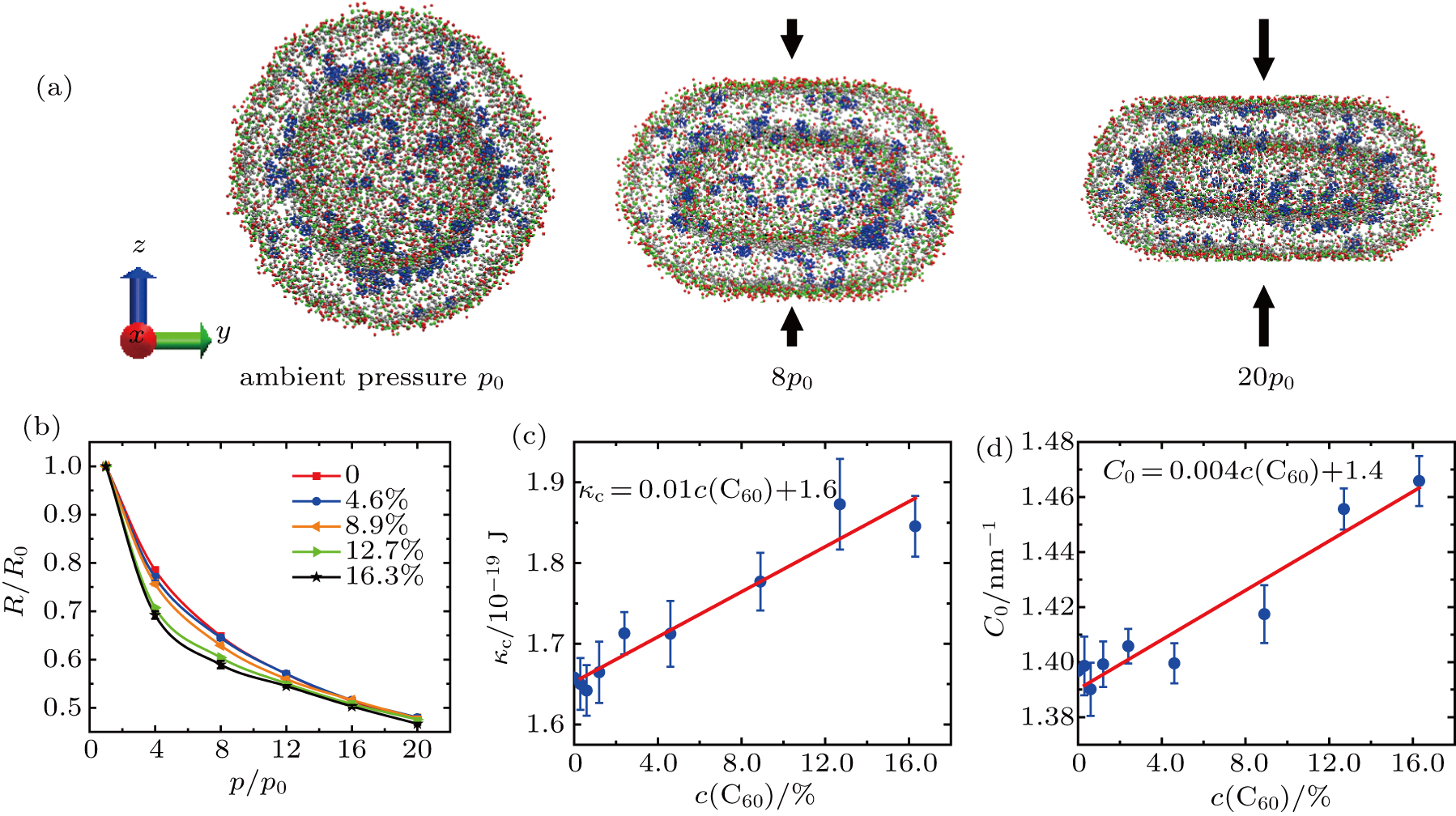
The typical deformation of vesicles under different vertical pressures at equilibrium is shown in Fig.
The bending modulus κc and the spontaneous curvature C0 of the vesicle membranes are obtained by fitting our simulation data to Eqs. (
Our results show that the bending modulus of the pure DPPC vesicle membrane is approximately 1.6 × 10−19 J, roughly in agreement with the values obtained in previous simulations and experiments.[49,52,53,55,58,59,70] It is suggested that our simulations and theoretic analyses should be reliable, though the size of vesicle used in our simulations is not so large that the thickness of membrane can be neglected. The bending modulus increases linearly approximately as the C60 concentration increases from 0 to 16.3%.
The spontaneous curvature of the pure DPPC vesicle membrane is 1.4 nm−1. It also increases linearly approximately with the increasing C60 concentration.
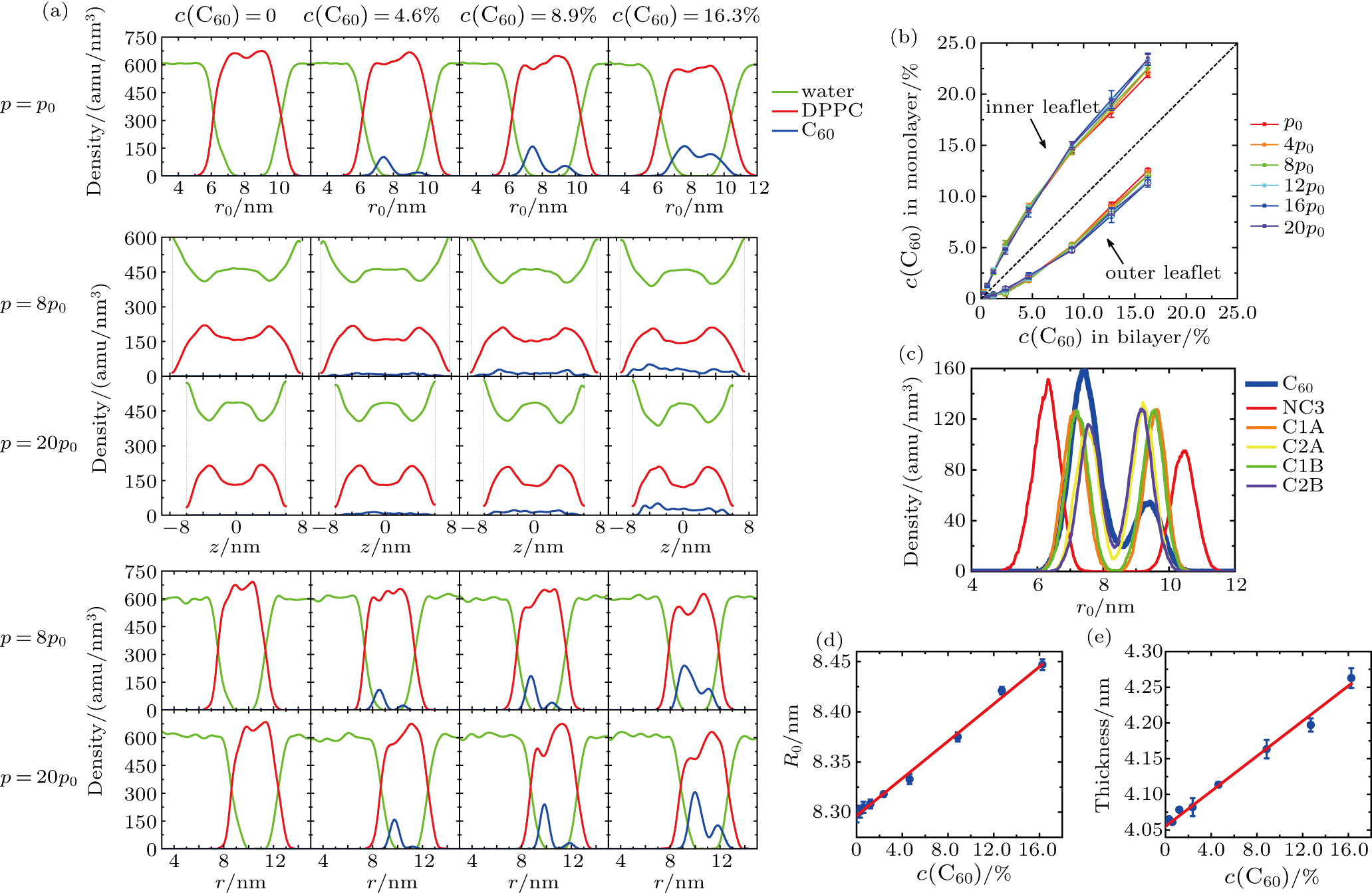
The density profiles of DPPC, water and C60 in the vesicles at different vertical pressures and C60 concentrations are shown in Fig.
According to the radial density profiles (density vs distance from the center of the spherical vesicle, r0) under ambient pressure (Fig.
The density profiles under pressurization are depicted by the density distributions along the z axis (Fig.
The C60 concentrations in the inner leaflet and the outer leaflet are quantitatively measured (Fig.
The radial density profiles of some CG beads under ambient pressure are illustrated in Fig.
Additionally, the infiltration of C60 into the bilayer changes the size of the vesicle membrane. Both the radius of the initial spherical vesicle and the thickness of DPPC bilayer increase linearly with the C60 concentration (see in Figs.
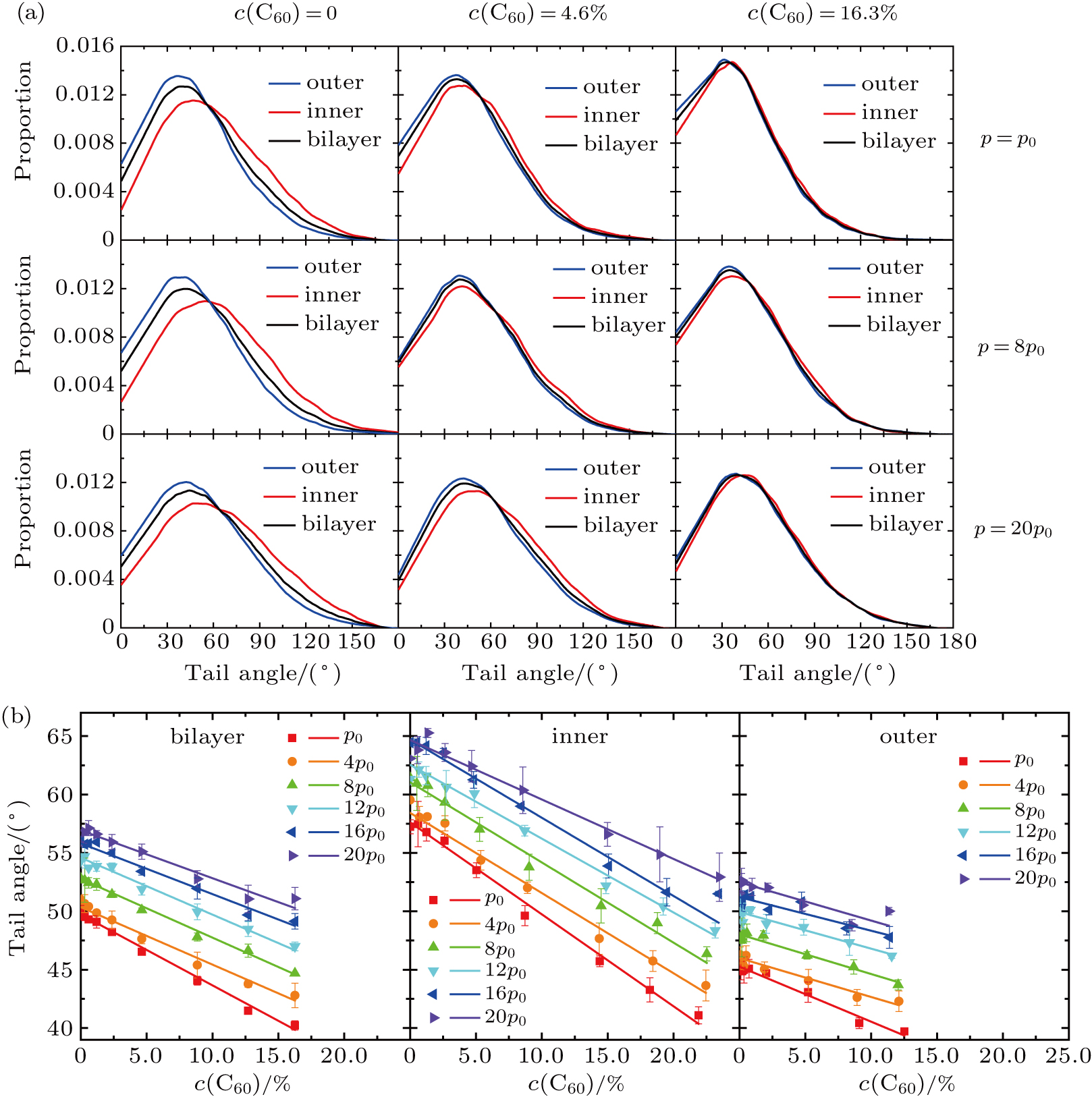
The angle between two carbohydrate tails of the lipid is chosen as the order parameter.[71] The tail angle distributions of membranes at diverse vertical pressures and C60 concentrations are illustrated in Fig.
The average of tail angles in the membrane is calculated, seen in Fig.
The broader distribution with a peak farther from 0° suggests that the packing of lipids is less ordered. Similarly, the smaller average of tail angles means the higher order of the vesicle membrane. Altogether, we could draw three conclusions: in a vesicle, the lipid packing is less ordered in the inner leaflet than in the outer leaflet, but the difference in lipid packing between the two monolayers becomes less obvious as more C60 nanoparticles enter the bilayer; the vertical pressurization forces the vesicle membranes into a more disordered state; the infiltration of C60 enhances the order of lipid packing.
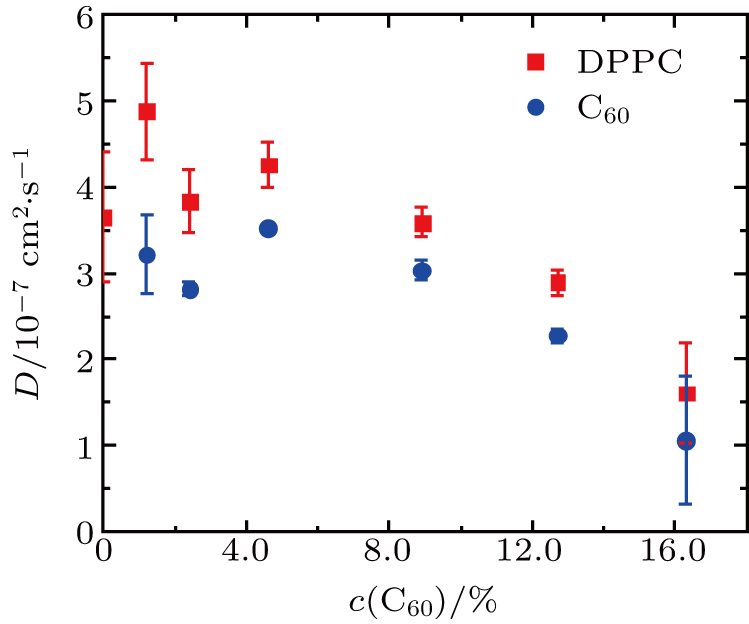
The diffusion coefficients of DPPC molecules and C60 nanoparticles in the vesicles under ambient pressure are shown in Fig.
According to our simulations and analyses, the native structures of vesicles and the atomic interaction between C60 and lipids affect the spontaneous infiltration and the uneven distribution of C60 in the bilayers. The infiltration and distribution of C60 nanoparticles, in turn, alter the sizes, the structural and the dynamic properties of the vesicles. The modulation of structures and dynamics has an further influence on the elasticity of the vesicles. On the one hand, C60 nanoparticles induce the order of lipid packing, reduce the fluidity of membranes, then strengthen the vesicle, and increase the bending modulus. On the other hand, C60 nanoparticles change the asymmetry between the two monolayers of the bilayer (i.e., the infiltration of C60 modifies the density profiles and the tail angle distributions of inner and outer leaflets), and thus alter the spontaneous curvature of the vesicle membrane.
We have explored the effect of C60 nanoparticle infiltration on the vesicles composed of DPPC lipid bilayers through CG MD simulations. The bending modulus and the spontaneous curvature of the DPPC vesicles with C60 nanoparticles of different molecular concentrations have been obtained based on the Helfrich spontaneous curvature model. The bending modulus and the spontaneous curvature of pure DPPC vesicles are approximately 1.6 × 10−19 J and 1.4 nm−1, respectively. It is concluded that both the bending modulus and the spontaneous curvature increase linearly approximately with the C60 concentration (0–16.3%).
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] |