Cite this Article
Yu Wen-Juan, Zhang Yu, Xu Ming-Zhu, Lu Xin-Miao. Dark count in single-photon avalanche diodes: A novel statistical behavioral model. Chinese Physics B, 2020, 29(4): 048503  
Permissions
Dark count in single-photon avalanche diodes: A novel statistical behavioral model
Yu Wen-Juan, Zhang Yu †, Xu Ming-Zhu, Lu Xin-Miao
School of Electronics and Information, Hangzhou Dianzi University, Hangzhou 310018, China

 

† Corresponding author. E-mail: yuzhang1978@163.com

Project supported by the Natural Science Foundation of Zhejiang Province, China (Grant No. LY17F010022) and the National Natural Science Foundation of China (Grant No. 61372156).

Abstract

Dark count is one of the inherent noise types in single-photon diodes, which may restrict the performances of detectors based on these diodes. To formulate better designs for peripheral circuits of such diodes, an accurate statistical behavioral model of dark current must be established. Research has shown that there are four main mechanisms that contribute to the dark count in single-photon avalanche diodes. However, in the existing dark count models only three models have been considered, thus leading to inaccuracies in these models. To resolve these shortcomings, the dark current caused by carrier diffusion in the neutral region is deduced by multiplying the carrier detection probability with the carrier particle current at the boundary of the depletion layer. Thus, a comprehensive dark current model is constructed by adding the dark current caused by carrier diffusion to the dark current caused by the other three mechanisms. To the best of our knowledge, this is the first dark count simulation model into which incorporated simultaneously are the thermal generation, trap-assisted tunneling, band-to-band tunneling mechanisms, and carrier diffusion in neutral regions to evaluate dark count behavior. The comparison between the measured data and the simulation results from the models shows that the proposed model is more accurate than other existing models, and the maximum of accuracy increases up to 31.48% when excess bias voltage equals 3.5 V and temperature is 50 °C.

PACS: ;85.30.De;;85.60.Dw;;85.60.Gz;;42.79.Pw;
Keyword:;single-photon avalanche diode;;dark count;;statistical behavioral modeling;;carrier diffusion;
1. Introduction

With the development of the complementary metal–oxide–semiconductor (CMOS) technology,[1,2] single-photon avalanche diode (SPAD) detectors based on this technology have been favored by researchers and have been applied to many fields, including laser ranging,[3] fluorescence lifetime imaging,[4] two-dimensional scanning imaging,[5] and other such applications because of their increased sensitivity, high gain coefficients, and increased response speeds.

However, CMOS technology gives rise to the generation of the dark count that constitutes the inherent noise in SPADs. Accordingly, this noise may cause photon counting errors and can considerably restrict the performances of SPAD detectors. To design the peripheral circuits of SPADs and ensure normal SPAD operations, a precise behavioral model for simulating the statistical characteristics of the dark count must be established. However, the early models described only the current–voltage (I–V) characteristics and ignored the statistical behavior of the dark count in SPADs.[6,7] Subsequently, other reports[8,9] proposed a behavioral model to predict the dark count. However, this simulation model considers only the thermal dependence of the dark count and ignores the electric-field-dependent tunneling effects. The effect of band-to-band tunneling (BTBT) on the dark count was also considered for the first time in Ref.[10], but the trap-assisted tunneling (TAT) mechanism was ignored. Recently, a comprehensive and accurate dark count model was proposed.[11,12] However, studies have shown that carrier diffusion in the neutral region can also cause the dark count[13,14] that has been ignored in the aforementioned dark count models.

In the present study, the dark current caused by carrier diffusion in the neutral region is deduced by multiplying the carrier detection probability with the carrier particle current from three neutral regions at the boundary of the depletion layer. Therefore, based on previous dark count modeling studies in Refs. [11,12], a more accurate theoretical and statistical model is deduced that simultaneously considers the effects of thermal generation, carrier diffusion, and TAT and BTBT mechanisms for the first time. Furthermore, unlike the existing statistical models of dark current, which consider the avalanche triggering probability and electric field strength as constants under the same excess bias voltage that is denoted as Vex in this paper, the parameters of the proposed theoretical dark count model are varied with depth, obtained by extracting the model parameters of the SPAD device as a function of depth of the depletion region under the same excess bias voltage, thereby improving the accuracy of the proposed dark count model. Finally, the developed theoretical model for the dark counts was implemented with Verilog-A (a hardware description language) to formulate a statistical behavioral model.

The rest of this paper is organized as follows. In Section 2 the construction of the proposed statistical model for the dark count is presented, In Section 3 the results obtained from simulations of model parameters are described. And finally in Section 4 some conclusions are withdrawn from the present study.

2. Methods
2.1. Structure of SPAD device

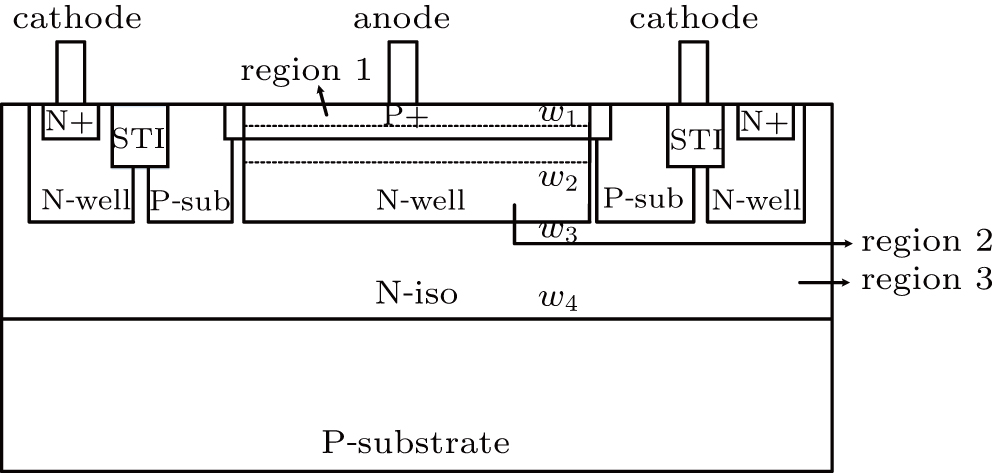
The device model used in this study is based on a standard CMOS process in an effort to form an SPAD with a virtual guard-ring structure, as shown in Fig. 1.[15] This model contains one of the most popular SPAD models, where P+ is the photosensitive region, and forms a contact with the N-well region to form the main P–N junction. Simultaneously, the P-sub structure and the shallow trench isolation (STI) structure prevent premature breakdown of edge, and the N-iso isolates the center of the device from the substrate, which effectively reduces the coupling noise and resolves the latch-up effects.

Fig. 1. Schematic diagram of device model for single-photon avalanche diode (SPAD),where w1 and w2 are depth of upper and lower boundary of depletion region, respectively, w3 is depth of lower boundary of the N-well, and w4 is depth of lower boundary of N-iso.
2.2. Theoretical model of dark counts

Dark counts are generally caused by device defects[14] and effectively correspond to the inherent noise in CMOS technology. In the absence of light, the dark carriers caused by the noise itself will produce the same avalanche as the photon-generated carrier and result in photon counting deviations. The dark counts are usually expressed as the dark count rate (DCR), i.e., the number of dark count occurrences per second (Hz). Studies have shown that dark count generation is mainly affected by four factors: Shockley–Read–Hall (SRH) thermal generation, TAT, BTBT,[8–12] and carrier diffusion.[13,14] The contributions from each of these four generating mechanisms are described in the following subsections.

2.2.1. Dark count generation owing to thermal generation

In general, the SRH theory is used to determine the rate of thermally generated carriers. In the depletion region, the density of electrons and holes are both much lower than the intrinsic carrier concentration. So the rate of carrier generation due to thermal generation can be expressed as[10]

where Et represents the recombination center level, Ei the Fermi level, Nt the recombination center density, r the carrier capture rate, T temperature, K0 the Boltzmann’s constant, and ni the intrinsic carrier concentration given by the following equation:

where Nc and NV are the effective density of states in the conduction band and the valence band, respectively. They can be expressed as

where and are the effective mass of an electron and a hole respectively, Eg(T) is the silicon bandgap energy at temperature T, and h is the Planck’s constant.

2.2.2. Dark count generation due to trap-assisted tunneling

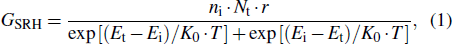
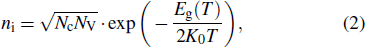
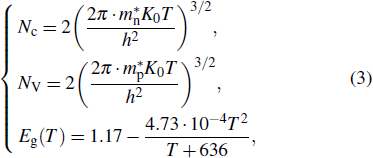
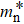
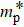
The rate of carrier generation caused by TAT can be calculated by the field-effect-enhanced SRH model based on the following formula:[11]

where Γ is the modulation factor.

2.2.3. Dark count generation due to band-to-band tunneling

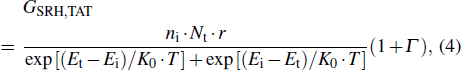
The rate of carrier generation due to BTBT can be given by the Hurkx model according to the following formula:[16]

where N0 is a material constant, D0 the correction factor, B a user-defined parameter, x the depth of the depletion region, and F(x) the magnitude of the electric field at a depth of x in the depletion region.

2.2.4. Dark count generation due to all three mechanisms

The overall rate of carrier generation in the depletion region can be expressed as

The dark count can be obtained by integrating the rate of carrier generation between (w2–w1) and w1.[17] As a result, the dark count generated by these three effects can be estimated by using the following equation:

where Ptr(x) is the probability of carrier avalanche triggered at position x in the depletion region and is expressed below.[18]

where Pe(x) and Ph(x) refer to the detection probability of electrons and holes at position x, respectively.

2.2.5. Dark count generation due to carrier diffusion

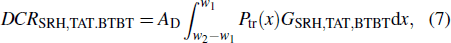
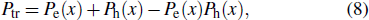
The minority carriers in the neutral regions will diffuse to the edge of the depletion region, which can additionally cause the dark counts. We define the undepleted P+ layer as region 1, the undepleted N-well layer as region 2, and the N-iso layer as region 3. Based on the carrier diffusion theory discussed in Ref. [19], we conduct the deduction in the following.

The dark count caused by electron diffusion in region 1 is equal to the electron detection probability multiplied by Collectione that is the electron particle current at the boundary of the depletion layer, and expressed by

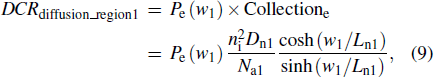
where Pe(w1) refers to the detection probability of electrons at the edge of the depletion region, Dn1 the electron diffusion coefficient of region 1, Na1 the doping density of region 1, and Ln1 the electron diffusion length in region 1.

Similarly, the dark counts in regions 2 and 3 are equal to the hole detection probability multiplied by Collectionh that is the hole particle current at the boundary of the depletion layer, i.e.,

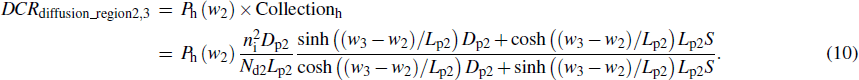
In this case, S is the surface recombination velocity at the junction surface formed by region 2 and region 3, and expressed as

where Dp3 represents the hole diffusion coefficient of region 3, Nd2 and Nd3 denote the doping densities of region 2 and region 3, respectively, and Lp3 is the hole diffusion length in region 3. Additionally, Ph(w2) refers to the hole detection probability at the edge of the depletion region, Dp2 the diffusion coefficient of holes in region 2, Nd2 the doping density of region 2, and Lp2 the hole diffusion length in region 2.

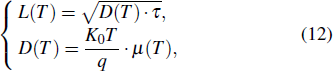
The diffusion length in Eqs. (9)–(11) can be calculated using the following expressions:

where q is the electron charge, τ the lifetime of the carrier, D(T) the diffusion coefficient, and μ (T) the mobility.

In summary, the dark count caused by carrier diffusion in the neutral region is the sum of the dark count caused by carrier diffusion in region 1, in region 2, and in region 3 and can be expressed by

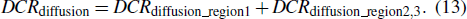
2.2.6. Proposed theoretical model of dark counts

According to the above discussion, we can formulate the proposed model of dark counts as

2.3. Behavioral model of statistical characteristics of dark counts

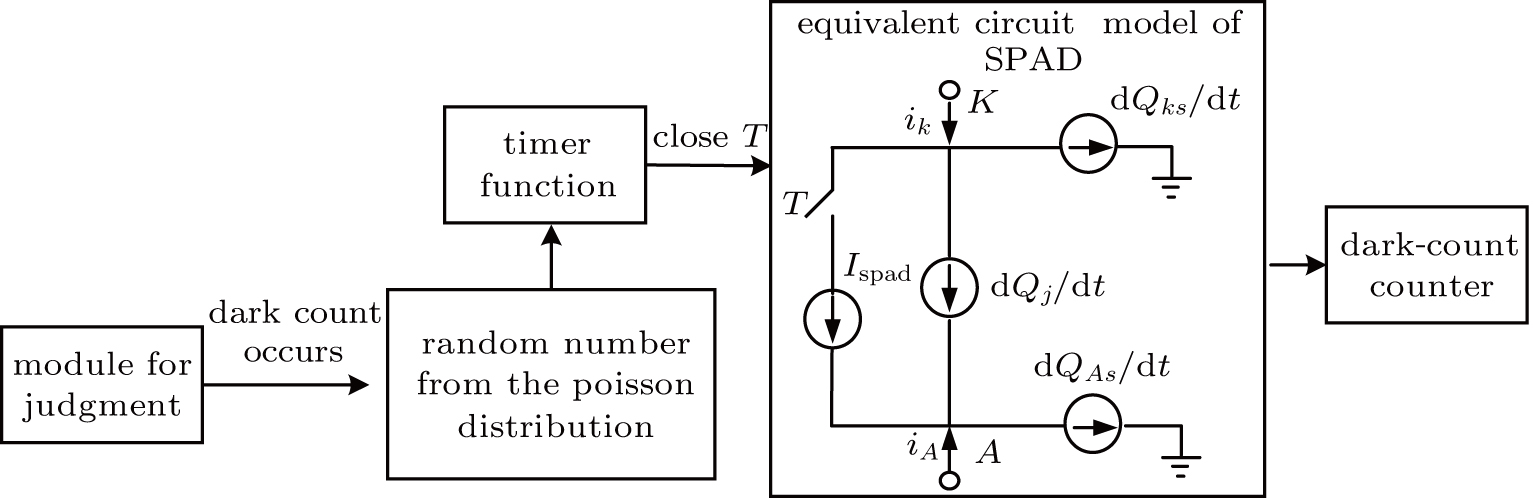
After successfully constructing the theoretical and statistical models of the dark counts, the behavioral model based on Verilog-A is built to describe the behavioral character of the dark counts in SPAD. This model includes five modules as shown in Fig. 2.

Fig. 2. Diagram of behavioral model of SPAD.

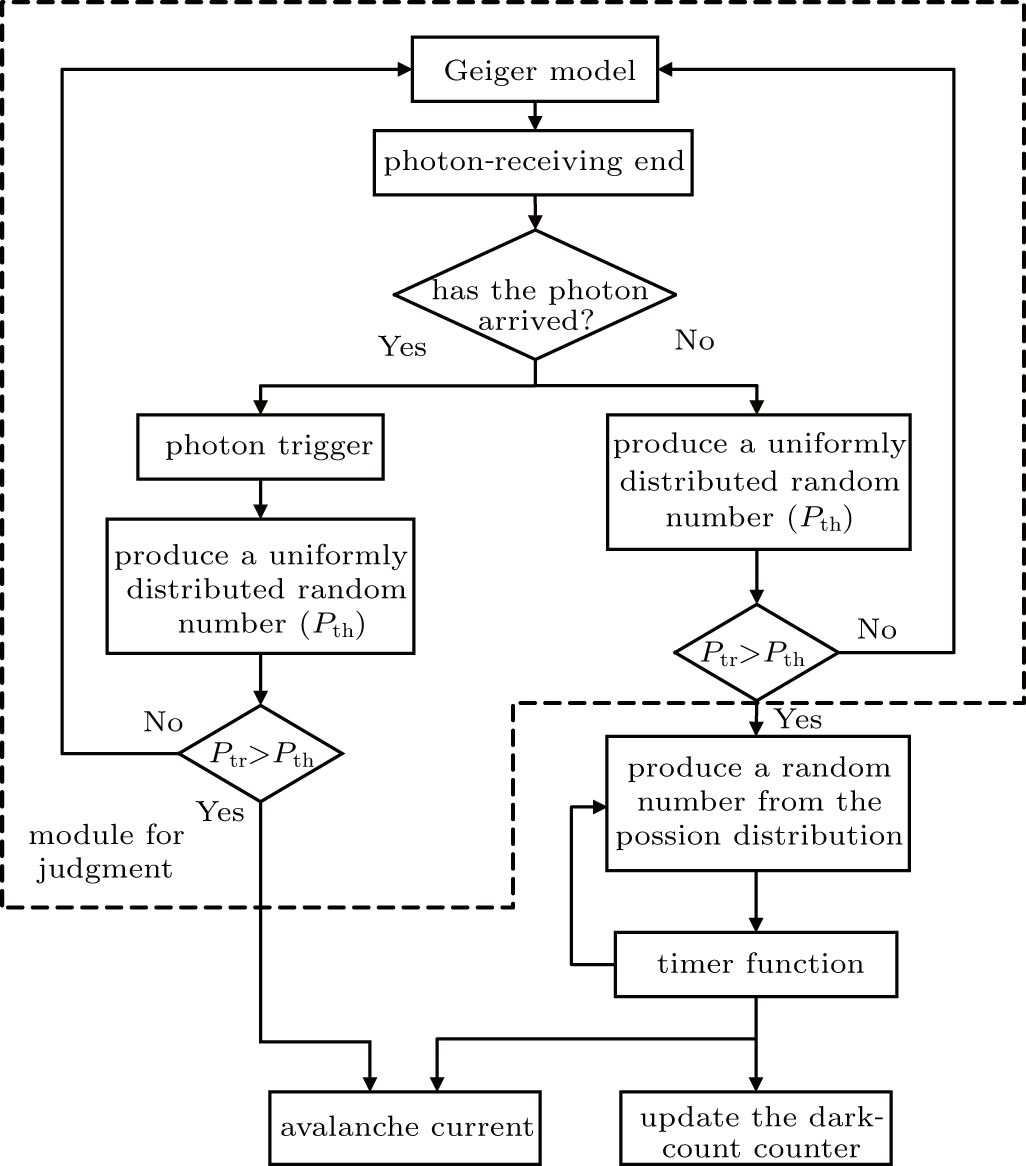
The judging module evaluates whether or not a dark count occurs. In the random number module the Poisson distribution is used to produce a random number. The timer function calls the random number to mark the moment at which a dark count occurs. The equivalent circuit model of SPAD generates a large current caused by the dark counts. The dark count counter module counts the number of dark counts. The logical relationships among the modules are schematically shown in Fig. 3.

Fig. 3. Working flowchart of behavioral model of dark counts.

When the SPAD detector works in the Geiger mode, the judgment module detects the voltage of the photon-receiving end to judge whether or not the photon has arrived. If the photon has arrived, the voltage of the photon-receiving end is high, and if not, the voltage of the photon-receiving end is low. No matter whether the photon has arrived, the judgment module generates a random number to simulate the actual probability of occurrence, which follows a uniform distribution[10] expressed as Pth, and the function $redis_uniform() in Verilog-A is used to generate these random numbers. The probability of triggering a carrier avalanche Ptr is then calculated from Eq. (8) and is compared with Pth. If Ptr is larger than Pth, the avalanche appears in the SPAD caused by the photon or dark counts. If Ptr is less than Pth, the judgment module will detect whether or not the photon has arrived. When the judgment module detects the occurrence of a dark count, the Verilog-A function $ redis_Possion (mean) generates a random number that matches the Poisson distribution, where the mean is the average generation time of the dark count, which can be express as tcg

which can be obtained from the proposed DCR model defined in Eq. (14). This random number is then substituted into a timer function to control the time of the dark count occurrence in the SPAD. At the same time, the increment of dark count counter is one.

3. Results
3.1. Extraction of model parameters

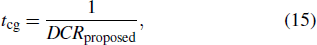
In most of the existing statistical dark count models, the avalanche triggering probability (including the hole triggering and electron triggering probabilities) and the electric field strength are obtained from empirical formula and are both considered to be constant for the same excess bias voltage. However, the changes of the corresponding parameter values at different depths of the depletion region under the same excess bias voltage are ignored.[8–10] In the present study, the Silvaco technology computer-aided design (TCAD) tool is used to simulate the SPAD device model to accurately extract the avalanche triggering probabilities and electric field strengths at different depths in the depletion region. Accordingly, using MATLAB tools, these extracted values are fitted with respect to the depletion depth. The obtained fitting functions are incorporated into Eqs. 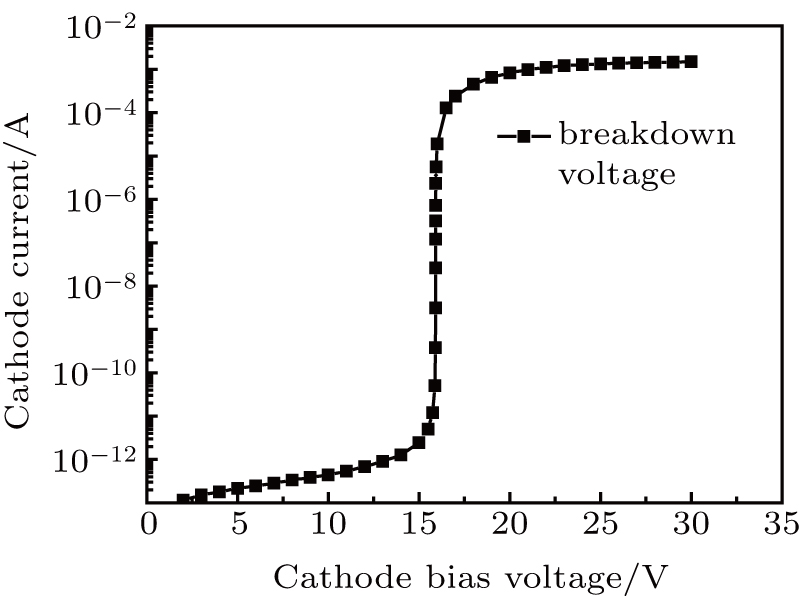(5)–(8) to simulate the performance of the actual device.

To ensure that the simulation results are as close as possible to the results obtained from the actual device reported in Ref.[15] and to extract more accurate physical parameters, the breakdown voltage is calibrated based on parameter adjustments for the SPAD device. These parameters are listed in Table 1. Figure 4 shows the I–V characteristics of the SPAD device used in this study. The breakdown voltage at room temperature is approximately 16.1 V, and it is consistent with the experimental result reported in Ref. [15].

Table 1.

Key parameters of Verilog-A model of SPAD.

.
Fig. 4. Current–voltage (I–V) characteristics of SPAD device.

The distributions of the hole and electron triggering probability and the distribution of the electric field strength as a function of depth at different excess bias voltages are shown in Fig. 5.

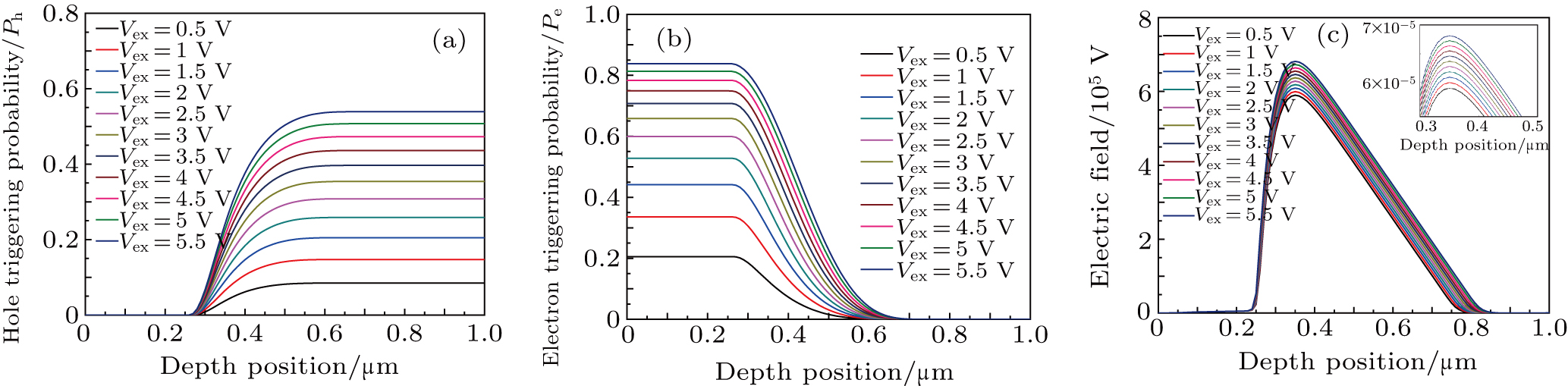Fig. 5. Extracted (a) hole trigger probability, (b) electron trigger probability, and (c) electric field strength at different depths.

Figures 5(a) and 5(b) demonstrate that the electron avalanche probabilities reach their own maximum value at the upper boundary of the PN junction, and gradually decrease to zero with depth increasing, while the hole avalanche probqbilities are highest at the lower boundary of the PN junction and decrease to zero at the upper boundary. Given that the collision ionization rate of holes is generally lower than that of electrons, the corresponding avalanche probability will be less than that of electrons. Meanwhile, figure 5(c) reveals that the peaks of the electric fields all appear near the center of the depletion region, and their corresponding magnified parts are shown in the inset. The key parameters of the Verilog-A model of the SPAD are summarized in Table 1.

3.2. Model simulation results and analysis

The proposed dark count statistical model is implemented by using the behavioral hardware description language of Verilog-A according to the flowchart in Fig. 3. To simulate the dark current performance of the proposed model in Cadence Spectre, the photon-receiving end of the SPAD in Fig. 3 is grounded during the simulation. At this time, the SPAD only generates avalanche currents caused by dark counts. Thus far, the dark count model in Refs. [11,12] has been the most accurate one and is close to the actual measured data in Ref. [15]; thus, the dark count model proposed here is compared with this model and with the actual measured data in Ref. [15] as well.

Table 2 shows the comparision among DCRs at different excess bias voltages in a range from 0.5 V to 5.5 V in steps of 0.5 V at room temperature. Each simulation is executed for 1 s, and the number of times the dark counts occur is recorded. This simulation is repeated 100 times at each excess bias voltage, and the average value is used to compare the results of the dark count model formulated in Refs. [11,12] with the actual measured data.

Table 2.

Simulated DCR as a function of excess bias voltage at 26.7 °C.

.

Table 3 shows a comparison among the DCRs at different temperatures in a temperature range from −30 °C to 50 °C in steps of 5 °C when the excess bias voltage is 3.5 V. Each simulation is executed for 1 s, and the number of times the dark counts occuris recorded. The simulation is repeated 100 times for each temperature, and the average value is used for comparing the data obtained in the dark count model proposed in Refs. [11,12] with the actual measured data.

Table 3.

Simulation of DCR as a function of temperature at Vex = 3.5 V.

.

Two indices are calculated to evaluate the proposed dark current model, where the variable Errorproposed represents the error of the proposed model relative to the measured data. The variable Errorprevious indicates the error of the existing model in Refs. [11,12] relative to the measured data. The variable Errorreduction is the decrement in the error in the existing model relative to that of the model proposed in Refs. [11,12], and the parameter Increased_accuracy is the increment in the accuracy of the proposed model relative to that of the existing model.

Tables 2 and 3 reveal that compared with the results from the existing models, the results from the proposed model are closer to the measured data, the accuracy and error reduction are improved under different excess bias voltages and temperatures. The maxima of accuracy increase and error reductions reach 31.48% and 2.39% respectively, when excess bias voltage equals 3.5 V and temperature is 50 °C.

4. Conclusions

In this study, a statistical model for the dark current is proposed to simulate the behavior of the dark current more accurately than the existing models. The proposed model is primarily based on this existing theoretical model but also reflects the effect of carrier diffusion. The developed statistical model of the dark current is implemented with Verilog-A. Correspondingly, the Cadence Spectre simulations that invoked this behavioral model confirm the validity of the proposed model. This is the first time that the effect of carrier diffusion on dark counts has been considered, where the important parameters in the proposed model are varied with the depth of the depletion region of SPAD device. The simulation results show that the DCRs from proposed method are closer to the measured data than those from the existing models. Effectively, the relative error is 2.39% lower than those from the existing models, and its accuracy is 31.48% higher than the existing models, when excess bias voltage equals 3.5 V and temperature is 50 °C. The proposed dark current model can offer a beneficial reference for accurately simulating the physical characteristics of SPADs and in turn, for designing the peripheral circuit for SPADs.

Reference
[1] Nie K M Xu J T Gao Z Y 2016 IEEE Sens. J. 16 1319
[2] Xu J T Shi X L Nie K M Gao Z Y 2018 IEEE Sens. J. 18 2729
[3] Zheng L X Wu J Shi L X Xi S Q Liu S Y Sun W F 2014 J. Semicond. 35 045011
[4] Acerbi F Frera A D Tosi A Zappa F 2013 IEEE J. Quantum Electron. 49 563
[5] Qu H M Zhang Y F Ji Z J Chen Q 2013 Laser Phys. Lett. 10 105201
[6] Zappa F Tosi A Mora A D Tisa S 2009 Sensors and Actuators: A Physical 153 197
[7] Mita R Palumbo G Fallica P G 2008 IET Circ. Dev. Syst. 2 207
[8] He Q Y Xu Y Zhao F F 2013 J. Semicond. 34 66
[9] Giustolisi G Mita R Palumbo G 2011 IEEE International Symposium on Circuits & Systems (ISCAS) May 15–18, 2011 Rio de Janeiro 773 776 https://doi.org/10.1109/ISCAS.2011.59 37680
[10] Cheng Z Zheng X P Palubiak D Deen M J Peng H 2016 IEEE Trans. Electron Dev. 63 1940
[11] Xu Y Zhao T C Li D 2018 Superlattices and Microstructures 113 635
[12] Xu Y Xiang P Xie X P Huang Y 2016 Semicond. Sci. Technol. 31 065024
[13] Teranishi N 2016 IEEE Trans. Electron Dev. 63 10
[14] Pagano R Corso D Lombardo S Valvo G Sanfilippo D N Fallica G Libbertino S 2012 IEEE Trans. Electron Dev. 59 2410
[15] Pancheri L Stoppa D Dalla Betta G F 2014 IEEE J. Sel. Top. Quantum Electron. 20 328
[16] Hurkx G A M De Graaff H C Kloosterman W J Knuvers M P G 1992 IEEE Trans. Electron Dev. 39 2090
[17] Haddadifam T Karami M A 2019 Chin. Phys. 28 068502
[18] Zhou P Li C F Liao C J Wei Z J Yuan S Q 2011 Chin. Phys. 20 028502
[19] Kindt W J 1999 Geiger mode avalanche photodiode arrays: for spatially resolved single photon counting PhD Dissertation Delft Technische Universiteit Delft in Netherlands