Cite this Article
Jean Willy Habimana, Li Xinwei, Hao Tan Yong, Chen Zhe, Cagirici Mehmet, Borayek Ramadan, Herng Tun Seng, Aaron Ong Chun Yee, Li Chaojiang, Ding Jun. Overview of finite elements simulation of temperature profile to estimate properties of materials 3D-printed by laser powder-bed fusion. Chinese Physics B, 2020, 29(4): 048101  
Permissions
Overview of finite elements simulation of temperature profile to estimate properties of materials 3D-printed by laser powder-bed fusion
Jean Willy Habimana, Li Xinwei, Hao Tan Yong, Chen Zhe, Cagirici Mehmet, Borayek Ramadan, Herng Tun Seng, Aaron Ong Chun Yee, Li Chaojiang, Ding Jun †
Department of Materials Science and Engineering, Faculty of Engineering, National University of Singapore, 9 Engineering Drive 1, Singapore 117576, Singapore

 

† Corresponding author. E-mail: msedingj@nus.edu.sg

Project supported by Singapore Maritime Institute and the Advanced Material & Manufacturing R&D Program (Grant Nos. SMI-2016-OF-04 and R261502032592).

Abstract

Laser powder bed fusion (LPBF), like many other additive manufacturing techniques, offers flexibility in design expected to become a disruption to the manufacturing industry. The current cost of LPBF process does not favor a try-and-error way of research, which makes modelling and simulation a field of superior importance in that area of engineering. In this work, various methods used to overcome challenges in modeling at different levels of approximation of LPBF process are reviewed. Recent efforts made towards a reliable and computationally effective model to simulate LPBF process using finite element (FE) codes are presented. A combination of ray-tracing technique, the solution of the radiation transfer equation and absorption measurements has been used to establish an analytical equation, which gives a more accurate approximation of laser energy deposition in powder-substrate configuration. When this new analytical energy deposition model is used in in FE simulation, with other physics carefully set, it enables us to get reliable cooling curves and melt track morphology that agree well with experimental observations. The use of more computationally effective approximation, without explicit topological changes, allows to simulate wider geometries and longer scanning time leading to many applications in real engineering world. Different applications are herein presented including: prediction of printing quality through the simulated overlapping of consecutive melt tracks, simulation of LPBF of a mixture of materials and estimation of martensite inclusion in printed steel.

PACS: ;81.20.Ev;;81.05.-t;;47.11.Fg;;42.55.Ah;
Keyword:;selective laser melting;;powder bed fusion;;finite element modeling;;laser absorption;
1. Introduction

The world is facing a technological revolution towards a fully computerized manufacturing where additive manufacturing would play an important role.[1,2] In material research and design, instead of using try-and-error methods, simulation has attracted a great deal of attention of researchers to minimize wasted time and means. Laser powder-bed fusion (LPBF) additive manufacturing (AM), also known as selective laser melting (SLM) is a complex process involving phenomena taking place under environmental conditions that make it difficult, sometimes impossible, to measure physical parameters using techniques available today.[3–7] These parameters are, for example, localized temperature that can reach thousands of Kelvins, as well as mass flow rate and localized pressure at that high temperature.[8–11] In such a situation, simulation is a way that can help to gain more understanding of the details of the process. Though a complex process increases a need for simulation, it also becomes difficult to achieve a reliable model. Inclusion of many parameters in a model increases the fidelity,[12] but affects the numerical computation cost at a point where even supercomputers cannot compute it in a reasonable time. Thus, modelling and simulation of SLM process can be carried out at different levels of approximation.[12] Before choosing the main physics to be included in the model, it is important to bear in mind the aim and application of the simulation model or a specific phenomenon intended to be the focus of the study, and the computation power at your disposal. In this review, one section will be reserved for a discussion about different levels of approximation used in our previous works and those commonly found in literature. Nevertheless, at all levels of approximation, some physics are crucial not to be ignored: laser absorption, heat transfers in the whole material and mass flow in the melt pool are the main physics considered in most of the LPBF simulation models.[13–22] However, experimental observations evidenced that in some particular ranges of power and scanning speed, during powder consolidation and melt pool formation, phenomena like splattering from the melt pool, ejection of powder particle, and extreme key hole formation can become significant.[9,10,23–30] Simulation models with improved fidelity would then include physics like wetting and consolidation of powder, handling of the movement of multiple phases, irradiance of hot surface, recoil pressure onto the melt pool surface and the interaction of laser beam and the melt pool.[8,16,31,32] Figure 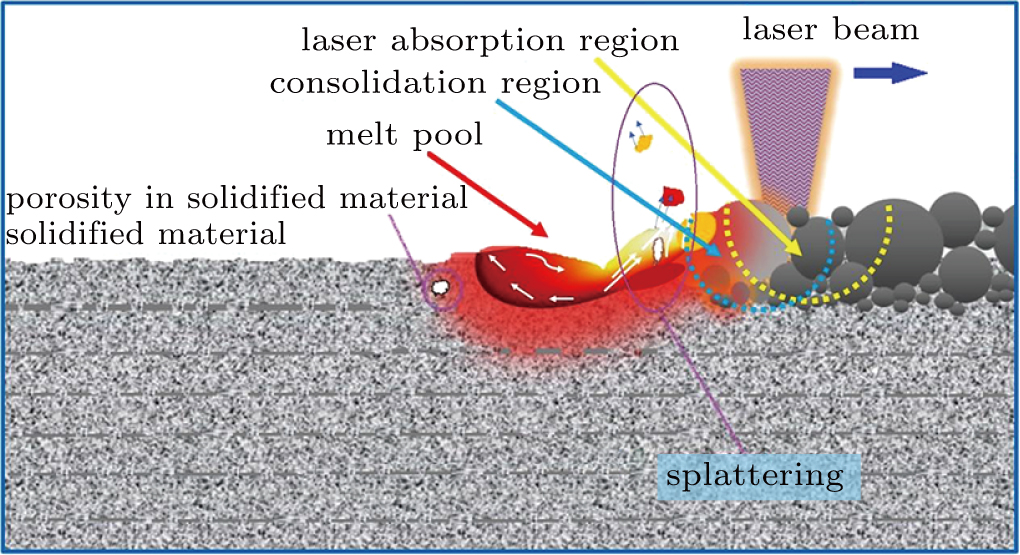1 gives a general illustration of the physics encountered in different working modes of LPBF process.

Fig. 1. General illustration of laser-powder bed fusion process showing different regions and phenomena likely to be present in different working modes of LPBF process.

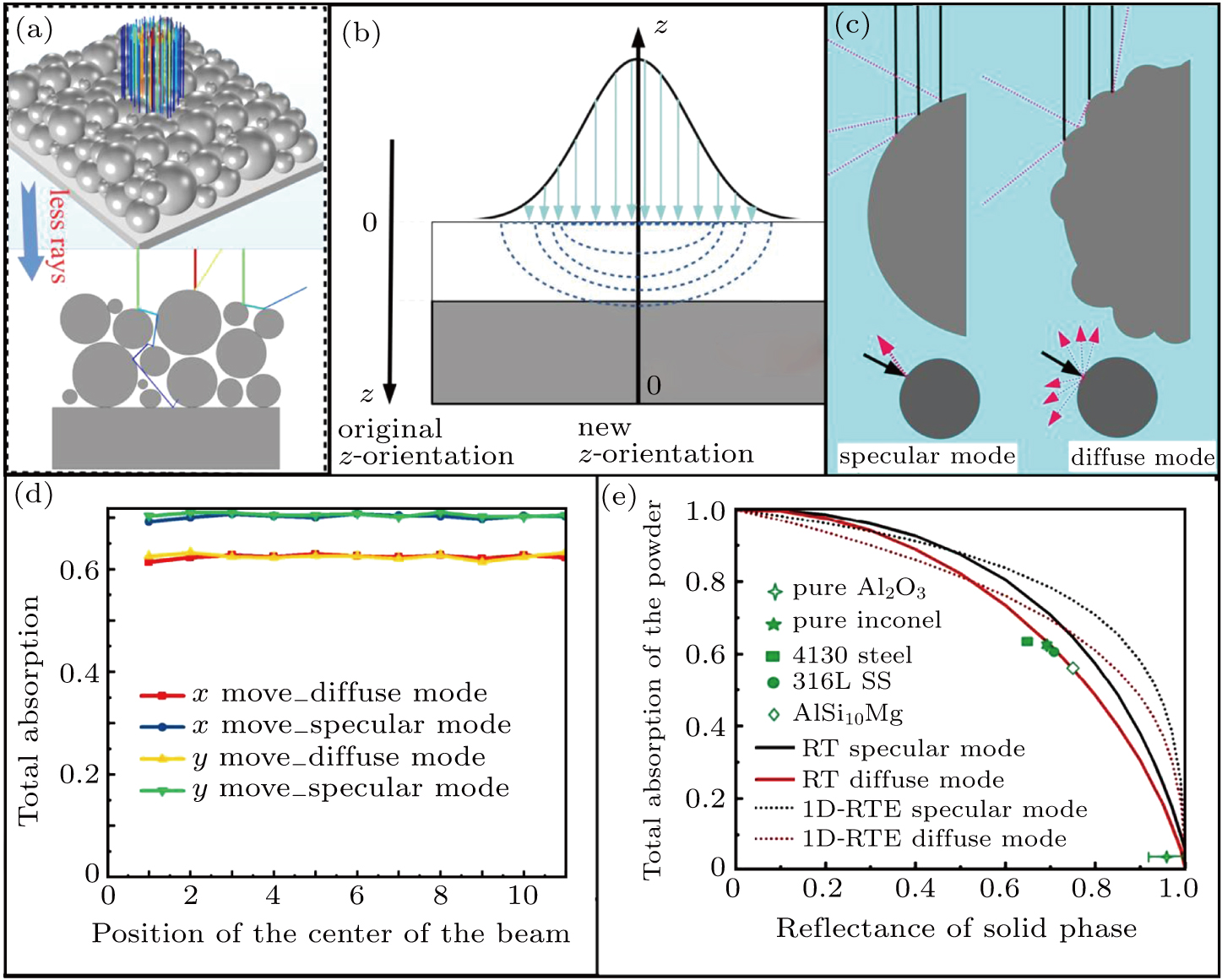
The starting point of simulation model for SLM process is laser energy absorption. Laser absorption in SLM is modeled in various ways. However, experimental observations of the time required for metal powder consolidation,[18,33] for relatively fast and sharp laser beam commonly used in SLM today, confirm that laser absorption is likely to happen in powder-bed before consolidation takes place. It is a different scenario from the conventional laser welding concept where a near-static laser interacts with the melt pool. Substrate-powder configuration is relatively hard to model using finite element (FE) methods. The choice between FE and other methods that can easily consider the granular nature of powder is controversial and beyond the aim of this review. In fact, FE is still the most common choice for macroscopic simulation in multi-scan patterns. Ray-tracing (RT) can be used to study laser penetration in the granular powder, which can more accurately approximate the laser energy absorption during powder bed fusion.[8] Nevertheless, the coupling of RT and heat transfer is computationally very heavy. This is due to a huge difference between the time steps used in both physics. In the end, it will limit the maximum laser scanning time to be studied and the size of the simulated domain. Let us mention that efforts have been made to consider the substrate-powder configuration in finite element simulation of SLM by using analytical expressions for energy deposition,[18,34] though the fidelity remains at a limited level.

Thermal properties of a material are of crucial role in SLM simulation. Basically, they are heat capacity, thermal conductivity and density of the material. The ranges of these physical parameters vary dramatically for different types of metal and ceramic,[35] which are the most common materials used in SLM. During synthesis of material composite trough SLM of mixed powders,[20,36] models for material properties of mixture are needed to estimate thermal and optical behavior.

Apart from the molten pool size and geometry or melt pool kinetics that have been used to evaluate the printing quality, the cooling rate and temperature gradient are even more important information from simulated temperature profile. These were intensively used to estimate micro structure formation[36,37] and martensitic nature of printed part.[38] However, limitation in the size of the simulated sample and the number of scanning lines, together with the accuracy of simulated cooling information, hinder the employability of this information. This hindrance has been overcome using a finite element model with high fidelity,[34] under assumption of a stable molten pool (conduction dominated region). The extent at which this assumption can hold is a crucial discussion not only for judging the fidelity of cooling information but also judging all features simulated compared to experimental facts.

As an alternative to simulation, scientists and engineers use simpler formulas based on the laser input energy density to quantify the printing quality with respect to process parameters like scanning speed, hatch, layer thickness, laser power and laser beam diameter. Many formulations are used, e.g., the linear energy density involving power and scanning speed,[39] volumetric energy density (VED) as defined by Ciurana, adding the consideration of laser beam diameter and layer thickness,[40] an alternative form of VED as defined by Gong et al. considering hatch distance instead of beam diameter,[41,42] and corresponding surface energy density ignoring the depth.[40] However, in many different publications, experimental studies have shown strong deviations from the empiric energy density formulations.[34,43,44] This also justifies the need of a computationally effective simulation model that can be used for a quick optimization of process parameter.

In this review, our recent works will be discussed to showcase current state of the art in some important components of an SLM simulation model. Different levels of approximation and corresponding output simulation information will be discussed first, together with possible applications and limitations. Various components of the model will be discussed. For heat transfer and mass flow, the impact of material properties on final printing results will be discussed and available material models will be analyzed. Modeling of laser absorption during SLM will be reviewed in detail; where the possibility of estimating the energy absorbed by a composite powder and estimation of corresponding thermal properties will be presented as part of a model for SLM of a mixture of powders. From the estimated temperature profile, the use of cooling information to study microstructure in stainless steel and ceramics, together with the study of martensite content in printed martensitic steel, will be showcased. Finally, a deep analysis of the weakness in energy density formulation commonly used to guide experimental parametric study will be carried out to highlight a correction proposed in our previous findings.

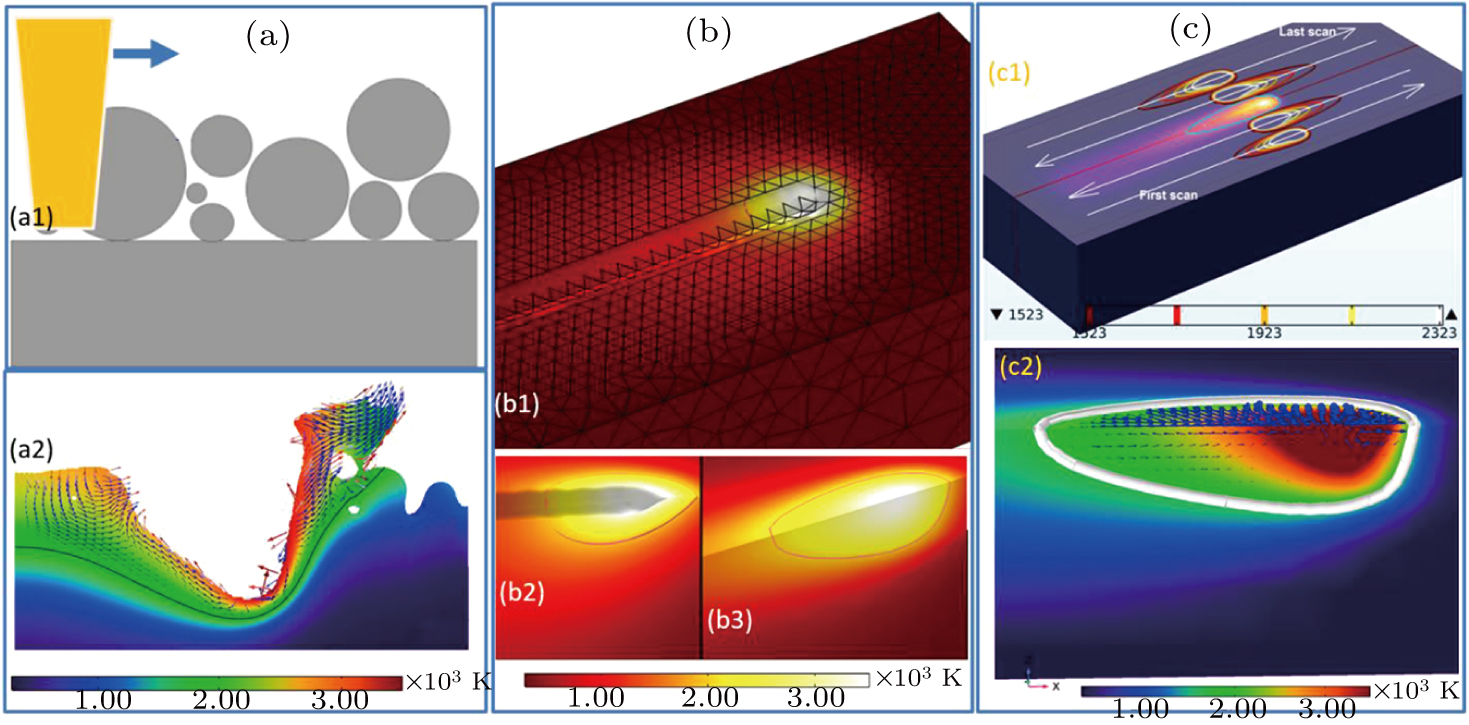
2. Different levels of approximation in FE simulation of SLM process

The most challenging issue in simulation of SLM process using FE methods is the implementation of the multiphase movements when solid powder particles consolidate, melt down and then solidify again. Apart from the solid-liquid interface, the model also needs to monitor the interface between the melt pool surface and surrounding air, on the one hand, and the escape of air pores between particles on the other hand. In different FE codes this can be implemented using different interface tracking methods (ITM). The most commonly found is the arbitrary Lagrangian–Eulerian (ALE) method of moving mesh.[45] The interface tracking adds another equation to solve, as a consequence, the computation suffers typically from long computation time due to highly nonlinear coupling between equations. When the aim of simulation is to use reasonable computation power to simulate a multi-scan and/or multi-layer process, it is more practical to model the balance of forces and mass flow in melt pool and powder bed without using explicit interface tracking. In Fig. 2, the three main levels of approximation found in literature and used in our previous works on 316L SS are shown. The explicit simulation of the multiphase nature of SLM process is shown in Fig. 2(a) using a laser power of 300 W and a scanning speed of 1400 mm/s. This way of modeling enables us to explore the role of surface tension and recoil pressure on the dynamics of the melt pool like splattering phenomena and origin of pores in the printed part. It was realized that high power working-mode tends to increase the instability in the melt pool zone and enhances the undesirable phenomenon of splattering and balling effects. From both experimental observation[9] and our preliminary simulations, it was realized that, in the normal working range of power and scanning speed, the melt pool becomes stable and the splattering becomes negligible after the laser has traveled a small distance on the first scanning line. Although this way of modeling captures some complex phenomena happening during SLM process, it may also suffer from a relatively poor approximation of powder distribution, which is most of the time sacrificed in order to make the geometry deformation passible. In addition, the limitation in geometry separation of the FE methods using ALE moving mesh, makes impossible the explicit representation of splatters and air pores. It requires less accurate approximation ITM to model the interface evolution of these different phases, which brings in a new approximation error. In our case, we used the phase field method provided in COMSOL Multiphysics.[46] More details and techniques used to overcome the issue of topology deformation in FE simulation of SLM process will be given in a later section. It is also crucial to mention that the explicit simulation of the topology deformation in SLM process is only adequate for the study of a local phenomenon. For example, the generation of an air bubble in the melt pool would depend on local parameters that are generally set randomly, though they have a significant implication to the simulated result, like a wide void in the powder bed. It is more practical to use this way of modeling to analyze specific cases found in LPBF process rather than a generalized parameter optimization across the whole printed material. In Fig. 2(b) a relatively less computationally heavy approximation is demonstrated. The moving mesh feature is used to capture the geometry deformation caused by the volume shrinkage when powder consolidates and solidifies. The initial fraction of solid material and air voids is modeled indirectly, using a uniform geometry, maintaining the energy and mass balance.[47] This way can lower the computation burden but still being able to have a filling of the melt truck impact on the roughness of the printed material. In Fig. 2(c) the most computationally efficient way of simulating SLM process is presented: five scanning lines at 175 W and 750 mm/s in (c1) and a single-scan at 300 W and 1400 mm/s in (c2).

Fig. 2. Different levels of approximation commonly used in simulation of SLM process (the case studied on 316L SS). In (a): the most ideal approximation considering the topological changes that follows the melt pool dynamics; (a1) gives the illustration and (a2) gives the simulated temperature profile and mass flow for P = 300 W and v = 1400 mm/s. In (b): approximation using geometry deformation from an initially uniform topology. In (c): multiple scan with P = 175 W v = 750 mm/s in (c1) and single scan with P = 300 W, v = 1400 mm/s in (c2) for an approximation without explicitly topological deformation.

All energy and mass balance are modeled without explicitly topological deformation. The fidelity of the model can still be improved by choosing good analytical models for energy and mass balance and good model of laser absorption. This way allows studying multiple scanning line or multiple layers and a generalized view of SLM process. However, it is crucial to note that the interpretation of the melt pool dimensions requires an understanding of the compensation between the size of powder layer and that of printed layer. Moreover, one important drawback of this way of modeling is the loss of some explicit information pointing to the direct observation of the phenomena like spattering and pores formation. Here we made a comparison mostly based on the computation power needed and applicability of simulation results in real world. A comparison of the estimated results from the three ways of simulation would be unreasonable as far as the melt pool morphology is concerned. Interestingly, the temperature profile estimated in all the three ways always points out similar results with minor deviations. The estimated velocity in the melt pool is also comparable in the two levels of approximation, being in the range of 0.1–5 m/s.

3. Models used to simulate interfaces and topological deformation in FE approximation of multiphase SLM process

Simulation of heat transfer using FE methods works under a discretization concept where a mesh grid is associated to the entire geometry. For SLM process, the air voids in the powder bed, the air bubbles in the melt, the air pores in the solidified material, liquid melt and liquid or solid mass splattered from the pool zone are subjected to displacements through the geometry during the process. The Navier–Stokes and the continuity equations are solved for the conservation of momentum and mass, as presented in the next section, coupled to the heat equation and BCs. To allow the coexistence and movement of all the possible phases in SLM, additional technics from the multiphase fluid flow theory[48,49] are needed. The most common way used in FE is the ALE moving mesh. This method is more accurate in simulating the interface between phases. Apart from the high computation burden and convergence issues, this method is also limited by the fact that it does not support topological changes. To get insight of bubbles formation and spattering as in Fig. 2(a), an ITM is needed. Two methods are the most commonly adopted; the level set method and phase field method. The methods are used to track the position of the interface between the two immiscible phases, accounting for differences in density and viscosity of the phases, as well as the effects of surface tension and gravity. Both the methods work by solving (one) additional transport equation, for the level set method, and (two) additional transport equations for the phase field method.[72] For the level set method, the interface is represented by an isocontour of a globally defined function called the level set function. Numerically, a smooth step function ϕ, equal to zero in a domain and one in the other, is used. The interface is set at the 0.5 isocontour and the movement of the interface is expressed as

where ε by default is constant within each domain and equals the largest value of the mesh size, γ is a parameter that determines the amount of reinitialization or stabilization of the level set function. A suitable value for γ is the maximum magnitude of the velocity field u.

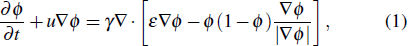
The phase field method includes more physics than the level set method and is more accurate as the interface is properly resolved by the mesh. For example, this method was used in literature in a multi-physics study of melt pool dynamics.[73] Separation of the two phases is modeled by a similar equation called the Cahn–Hilliard equation in the following:

where γ[(m⋅s)/kg] is the mobility, λ [N] is the mixing energy density, is the capillary width, in which σ stands for the surface tension coefficient [N/m], and Q′ is the source term that counts for ejected mass (vaporization and splattering). However, the phase field method requires relatively higher computation power compared to the level set method as it adds two additional transport equations versus one transport equation for the level set method.

4. Model of heat transfer and mass flow
4.1. Material property

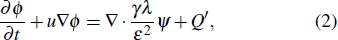
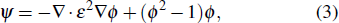
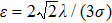
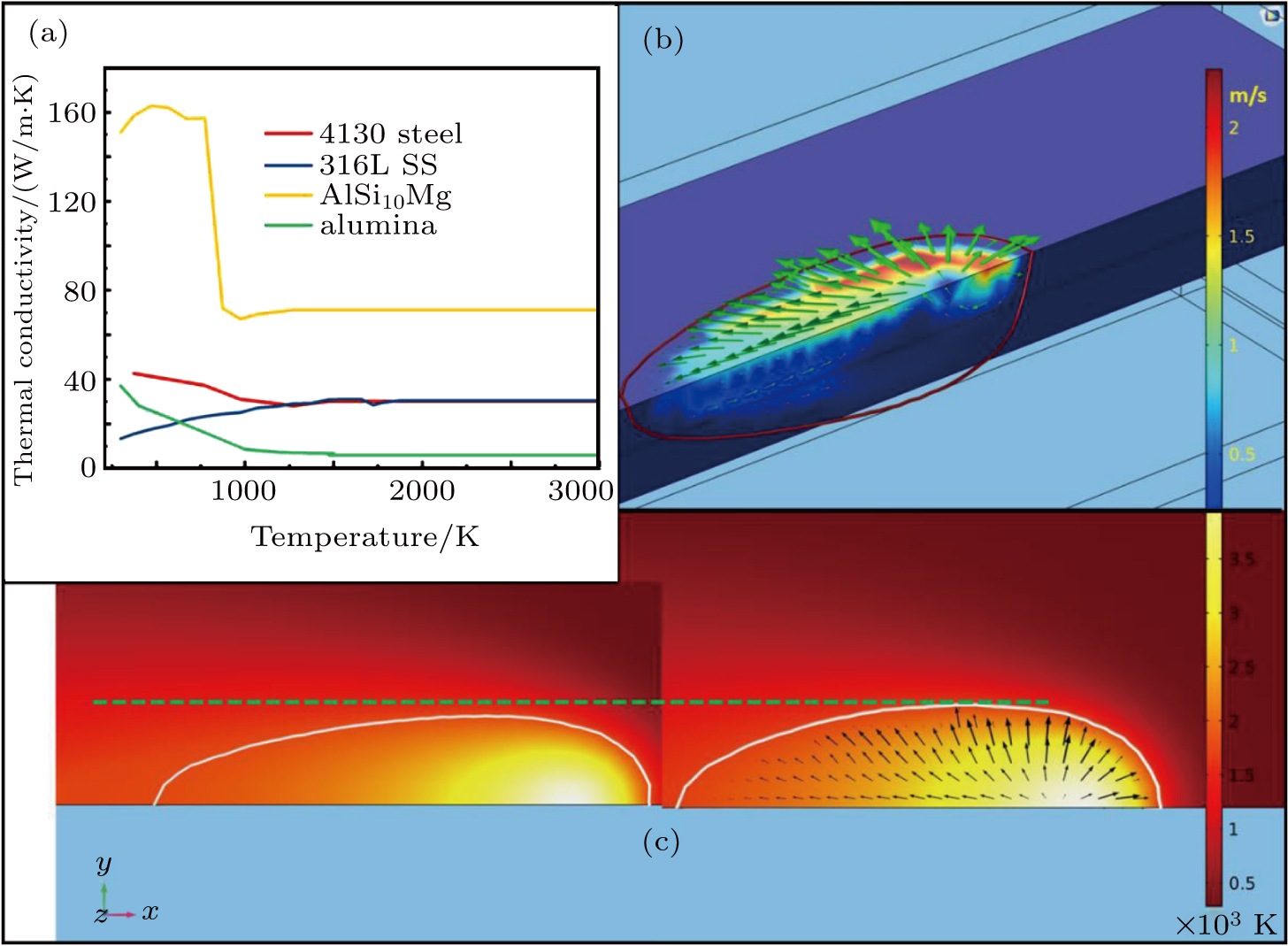
Material properties are the basis ground for material processing exploration. In LPBF process, thermal properties have high importance. However, the optical properties of material also play big role in defining the portion of laser energy flux to be used or wasted. In this section we will focus more on thermal properties. Optical properties will be discussed in detail in a later section about laser absorption. Heat capacity, density and thermal conductivity are the basic properties. Though some researchers assume constant values, models with higher fidelity require to define these properties as functions of temperature. For example, the temperature dependence of thermal conductivity of steel, aluminum alloy and alumina are plotted in Fig. 3(a). From the image, one can realize that thermal conductivity of AlSi10Mg alloy and alumina decreases about three times when the temperature changes from room temperature to near melting temperature.[35] In steels, research has indicated that carbon content, instead of other compositions, has a significant influence on the thermal properties and sensibility to temperature of carbon steel.[50] Contrarily, changes in heat capacity and density generally have the same trends for different materials. Density reduces with increasing temperature where a steep decrease is observed at the melting temperature due to solid-liquid volume change. Heat capacity changes in the opposite way. The most challenging issue is to estimate thermal properties for powder bed. The most accurate way to estimate thermal conductivity of powder is the variant form of the Zehner–Schlünder’s equation proposed by Sih and Barlow[51] as mentioned in Eq. (4). It was shown to give results that are comparable to experiment for different types of materials.

In the above equation, k is effective thermal conductivity of the powder bed, kg is thermal conductivity of the continuous gas phase, ks is thermal conductivity of the skeletal solid, φ is the porosity of the powder bed, kR is thermal conductivity part of the powder bed owing to radiation, denoted by Damköhler’s Eq. (5) below. Here ϕ is flattened surface fraction of particle in contact with another particle (it is equal to the flattened surface area divided by the cross-sectional area of the particle); ϕ = 0 when there is no contact for the particles; ϕ = 1 when there is complete particle contact. B is deformation parameter of the particle; B = 1 when the particle surface is that of a sphere; B < 1 when it is a prolonged needle; ∞ > B > 1 when it is a barrel-like body. B may be approximately calculated from the porosity φ of the powder bed by Eq. (6).

In Eq. (5), xR is the effective length for radiation between particles or the particle diameter of the powder in meters, σ = 5.67 × 10−8 W⋅m−2⋅K−4, T is the mean absolute temperature of the powder bed, and ε is the emissivity of the powder bed. This theory of Sih and Barlow in Eqs. (4)–(6) was used, for example, to estimate the heat conductivity of powder bed from that of bulk material for AlSi10Mg.[52]

Fig. 3. (a) Temperature dependence of thermal conductivity of bulk materials. (b) Velocity field and velocity magnitude in the melt pool of 316 SS. (c) Comparison of the melt pool size when the flow in the molten pool is considered (right) and when the flow is negated (left).

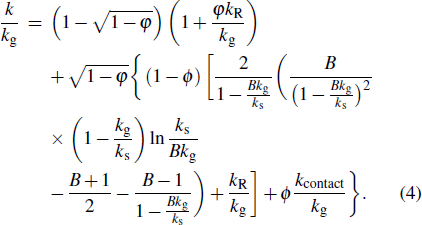
In our works, temperature-dependent values for heat capacity, density and thermal conductivity are used from literature for bulk materials. Heat capacity and density of the powder bed were approximated from those of bulk metals by linear combinations of properties of gas and bulk metal according to the porosity. Thermal conductivity of powder bed is model using the model of Sih and Barlow mentioned above.

4.2. Solid-liquid phase change in LPBF

One of the most important phenomena is solid-liquid phase transition when laser hits the powder and liquid-solid reverse phase change when the melt cools down. The total volumetric enthalpy H, which is the sum of sensible and latent heats, can be given as follows:

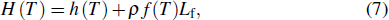
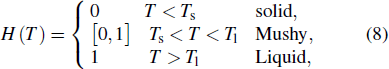
where h(T) is the sensible enthalpy function (without phase change), ρ is the density, f(T) is a liquid fraction function, Ts is the onset solidification temperature, Tl the onset liquidus temperature and Lf is the latent heat of fusion.[53]

In some materials, phase change can be modeled as isothermal phase change, reducing the mushy zone to a point, which is the melting point Tm. However, for metals, experimental results show that the mushy zone is very important[35,53–55] and is a characteristic of a material. This is testified by a considerable shift in enthalpy throughout the mushy zone which can dramatically change from one metal to another.[35] During numerical calculation, because the two phases possess different physical properties, this could create in the numerical model non-physical discontinuities which need to be addressed. In most of the numerical simulation software, this is implemented using apparent heat capacity[56] augmented in the mushy zone to consume the enthalpy of fusion as mentioned in the following equation:

where δCP is an apparent change in the heat capacity in the mushy zone, and is the heat capacity without phase change. In Eq. (10), ΔT is the length of the mushy zone and Tm is the characteristic melting point of the material.

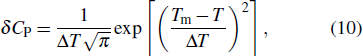
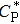
In our works we have used the above method to treat phase change during LPBF. Also, in our computation effective approximation, we have considered powder-to-solid transition together with an equivalent method to achieve volume shrinkage and material removal in FE as developed by Loh et al.[47]

4.3. Heat conduction and boundary conditions

The zero-heat-flux setting on all boundaries other than the top surface, mostly adopted in FE simulation of LPBF, does not represent the real situation in LPBF, where a small chunk of material of about 1 mm3 is considered. In reality, this small domain is imbibed in an infinitely large material with which they exchange heat. To overcome this difficulty, we used the “infinite element” feature provided in COMSOL Multiphysics[46] to describe a small sample imbibed in an infinite element of the same material. Heat transfer in the geometry is described by the heat equation:

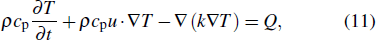
where T is the temperature, u is the mass velocity, ρ is the material density, cp is the heat capacity, k is the thermal conductivity and Q is the laser energy per absorbed unit volume. In the general model used in our works, boundary conditions are described by Eq. (12), in which the heat liberated by surface thermal radiation and the heat exchanged with the neutral gas by convection are applied on top surface. In the expression, ε stands for surface emissivity, σ the Stefan–Boltzmann constant, To the ambient temperature, H the height of the geometry, and h the convective heat transfer coefficient.

4.4. Mass transfer

Once vaporization temperature is reached, the latent heat of vaporization and recoil pressure are considered using the approximation of Semak and Matsunawa.[11] In the liquid region, the melt pool is subjected to the recoil pressure, Marangoni effect and volume forces. Navier–Stokes and continuity equations are used to model the laminar flow in the molten pool,

where P is the pressure, I is the three-dimensional unity tensor, μ is the viscosity of the melt, F is the sum of all other forces. During topological changes, the ITM discussed above helps to track the air-liquid or air-solid interfaces according to Eqs. (1)–(3), whereas in our computationally effective approximation, Marangoni effect is modeled by a shear stress on the upper surface of the melt pool (Eq. (14)). Equation (15) also gives the volume forces in the molten pool. In the expressions s is the melt pool top surface, γ is the surface tension, dγ/dT is the coefficient of the surface tension characterizing a given material, Tref is a reference temperature taken to be the melting point in our works, ρref is the reference density taken at temperature Tref and ρ is the temperature-dependent material density. Liquid-solid separation is reached using a smooth shift of the viscosity from a value of liquid viscosity, in the liquid temperature range, to an infinitely high value in the solid temperature range.

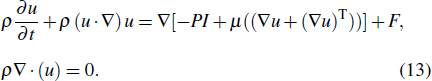
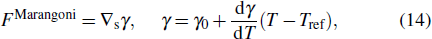
Values of parameters used in simulation can be found in our previous works.[34,38,57] The mass flow results obtained for 316L SS[57] proved a significant role of mass flow consideration in the model, which enhances the overall heat flow and melt pol expansion. In Fig. 3(b), on the top surface, results reveal a movement of the melt from the region of highest temperature gradient towards the boundary of the melt pool. This causes melt pool expansion due to heat convection. In Fig. 3(c), melt pool sizes are plotted when the flow in the molten pool is considered and when the flow is negated. The two images captured at the same magnification and from exactly the same model-geometry show a difference of about 9 μm in size of the whole melt pool measured on the top surface. Note that a scale factor of 1.5 × 10−5 is used to match the readings of the geometry length and velocity magnitude.

5. Laser absorption

In Eq. (11), Q refers to the total energy absorbed by the material from laser. This section shows how the model for describing Q-term is crucial. The simplest most adopted form in FE simulation of LPBF process is the surface energy flux absorption model, in which a Gaussian heat flux is deposited on the top surface.[12,13,16,19,20,22,37,47,53,58–60] This way ignores powder parameters like particle size, powder packing and powder layer thickness. A more realistic method uses average-medium volumetric energy theory with various forms of an exponential decay law in the following equation:[15,57,61]

The surface energy flux approximation can be easily deduced from Eq. (16) by omitting the z-decay expression and corresponding normalization factor δ. In the equation, p1(t) and p2(t) are functions controlling the laser position during scanning: for a single line scan along x-direction p1(t) = vt and p2(t) = constant; v is the scanning speed and t is the scanning time. A is the total powder absorption rate, P is the laser power, and r is the beam radius of the laser source.

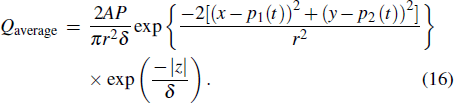
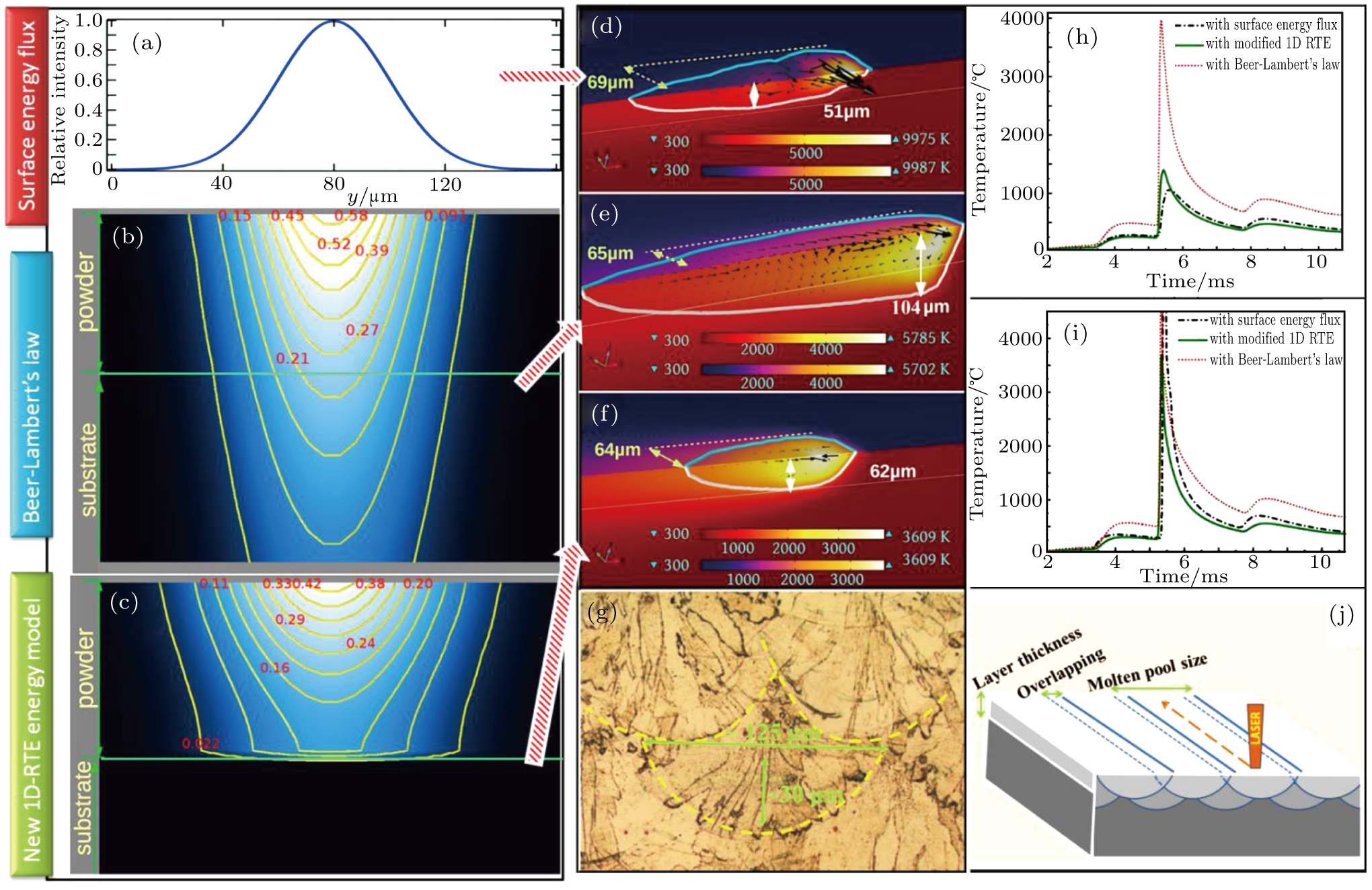
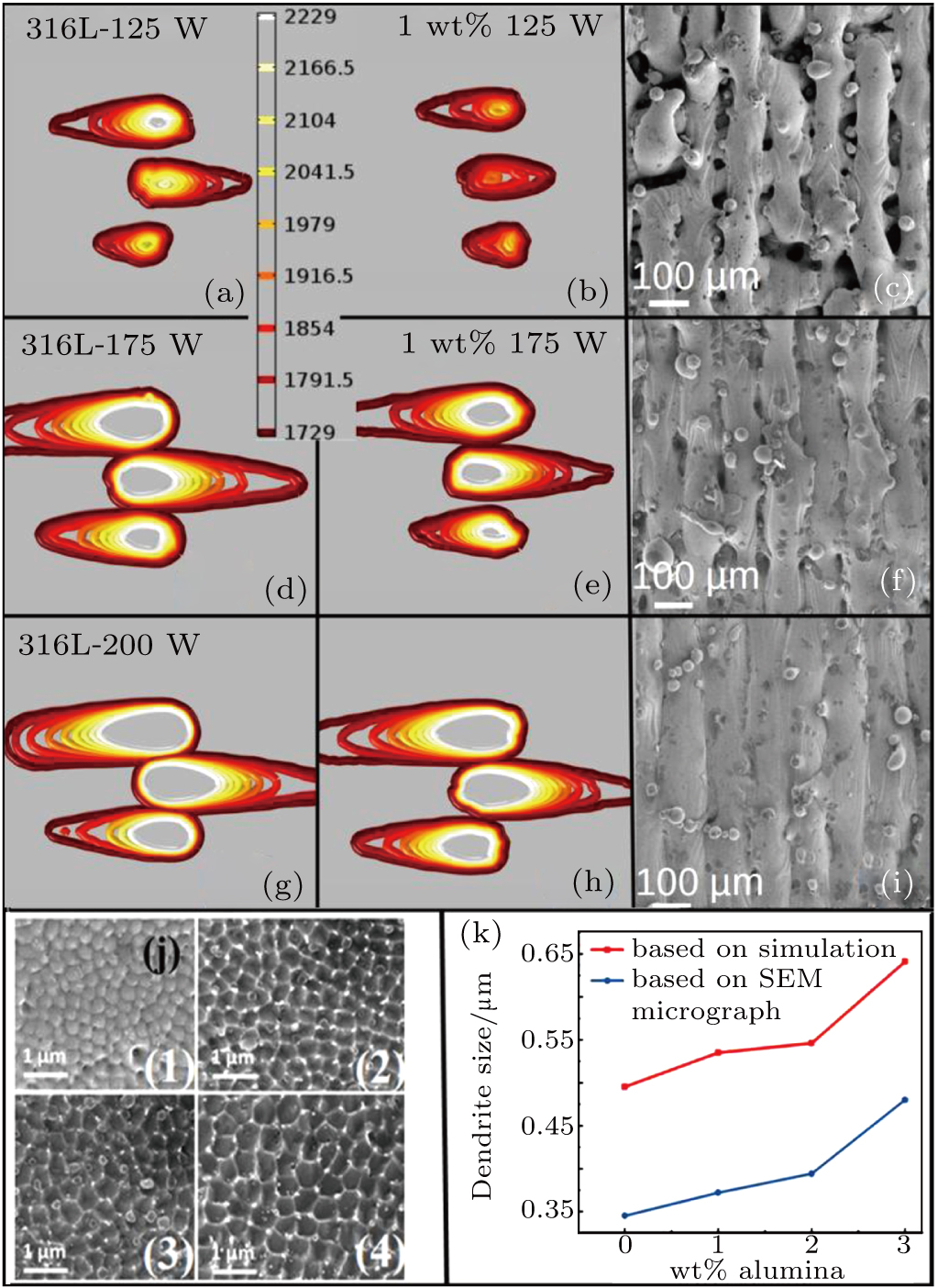
Though an average radiation penetration depth is considered in the previous methods, the granular nature, the effect of reflection by substrate, multiple reflections in powder, forward and back scattering phenomena are not captured in both the models. However, numerical simulation and experimental measurement have proven that the intensity and distribution of laser absorption in powder bed is far deferent from the above approximation.[62–64] Ray-tracing (RT) has been proven to be the best way to estimate radiation absorption during LPBF.[8,62,63,65,66] In our previous work,[34] it was demonstrated that RT results using diffuse mode, as illustrated in Figs. 4(a) and 4(c), coincide with the experimental optical measurements for different materials including steel, aluminum alloys, Inconel and alumina. Nevertheless, RT finds difficulties to couple directly with FE heat transfer due to extremely deferent time steps for the two physics. An alternative way is the use of analytical solution of one-dimensional radiation transfer Eq. (1D-RTE) proposed by Gusarov and Kruth[67] in a substrate-powder setting whose idea is illustrated in Fig. 4(b). Unfortunately, the comparison with two-dimensional (2D) numerical solution of the RTE[68] has shown that the 1D-RTE analytical solution overestimates the axial deposited energy due to radial broadening effect not captured in 1D approximation. That is also confirmed by comparison with RT and experimental measurements in Fig. 4(e). Using a data fitting of RT and experimental results, the 1D-RTE analytical model was modified[34] as in Eqs. (17)–(19) and can efficiently be used in FE simulation of LPBF process.

In the expressions, l is the powder layer thickness, a is the eigenvalue factor defined by Eq. (19) for diffuse mode, R is the solid surface reflectance, β is the extinction coefficient.

Fig. 4. (a)–(c) Illustration of RT, RTE and diffuse mode respectively, (d) total absorption approximated by ray tracing vis-à-vis the position of the beam and (e) total absorption obtained by experiment, RT and 1D-RTE in a deep powder bed.

Figure 5 summarizes the impact of laser energy deposition modelling on the final results of an FE simulation model of LPBF process. From absorption distribution in Figs. 5(a)–5(c), one can realize how the consideration of radiation reflection by the substrate helps to ovoid the overestimation of both total absorbed power and power penetration beneath the powder bed. Therefore, from Figs. 5(d)–5(f) we can see the shape and size of melt pool, the maximum temperature and mass flow rate in the pool estimated using different models for Q differ much. Due to errors in maximum temperature estimated, the accuracy of the cooling rate estimated also depends on Q model used as mentioned in Figs. 5(h)–5(i). As shown in on optical Microscopy image in Fig. 5(g), micro dendrite evolution depends much on melt pool patterns and scanning strategy as illustrated in Fig. 5(j). From this, one should bear in mind that the model of Q used would also affect any micro structure prediction using simulation.

Fig. 5. Effect of laser energy absorption model on the simulated temperature profile in SLM. (a)–(c) Absorption intensity and distribution using surface flux, volumetric exponential decay and modified 1D-RTE models respectively. (d)–(f) The corresponding melt pool morphology, T-profile and velocity field simulated. (h)–(i) The corresponding simulated cooling curves at a point on top surface and at a point on the bottom of built layer respectively. (g) OM image of the heat affected zone in printed material. (j) Illustration of scanning patterns.
6. Modelling LPBF process for of a mixture of materials

LPBF of powder mixture is important, for example, when making metal matrix composites (MMC). To simulate the process, a model for laser absorption and models for material properties of mixture are needed. The Bruggeman model is used to approximate the thermal conductivity of the mixture as in the equation[69]

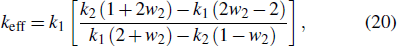
where subscripts 1 and 2 refer to materials 1 and 2, w is the weight percentage. Heat capacity, density and latent heat of melting for the mixture are approximated using simple volume weighted linear combinations. During phase change, the solidus temperature (Ts) and the liquidus temperature (Tl) play an important role. Before melting of the powder mixture, two materials are separated. It is more reasonable in calculation to use Ts of the mixture to be the lowest Ts and Tl of mixture to be the highest Tl.

Optical properties of the mixture can be well approximated in the framework of 1D-RTD if all components have a relatively high reflectance.[67,68] This was adopted in our FE model, for example, to study LPBF of the mixture of 316L SS and alumina up to 3 wt%.[36] Figure 6 summarizes the results of that study. For a power of 125 W the simulated melt truck for pure 316L SS, simulated melt truck for 316L SS/1 wt% alumina, and SEM images of printed melt truck for 316L SS/1 wt% alumina are presented in Figs. 6(a), 6(b), and 6(c), respectively. The simulation model is able to predict the lack of melt truck overlapping, which is essential for mechanical properties of printed parts. By a systematic increase in power to 175 W in Figs. 6(d)–6(f) and 200 W in Figs. 6(g)–6(i), one can see an increasing overlapping. High magnification scanning electron microscopy (SEM) images in Fig. 6(j) shows how the dendrite size increases when alumina content increases from 0 wt% to 3 wt% in sub-images (1)–(4), respectively. For austenitic SS, the cooling rate and dendrite size λ can be presented mathematically with the relation .[70] Using the estimated cooling rate, it is shown that the same trend is also expected from simulation.

Fig. 6. (a), (d) and (g) Simulated molten pool tracks along the scanning lines for 316L SS. (b), (e) and (h) Simulated molten pool tracks along the scanning lines for 1 wt% alumina. (c), (f) and (i) The corresponding experimental results for 1 wt% alumina. (j) High magnification SEM images of cellular dendrites. (k) Dendrite size trend comparison of experiment and simulation.
7. Estimated cooling rate and martensite content in printed steel

Multiple scan simulation provides cooling history in the built material. This information is of paramount importance in approximating in-process tempering effect due to scanning of multiple consecutive lines and layers. In a previous work, the simulated cooling curves of an LPBF process of AISI 4130 steel helped to understand the final martensite of printed material and the corresponding mechanical properties.[38] Figure 7(a) compares the cooling rate range in laser 3D-printing to the continuous cooling transformation (CCT) diagram estimated for 4130 steel from both calculation and experiment in a separate research.[71] It was realized that the cooling rate, in all the possible combination of parameters in SLM280L machine, is high enough to solidify in martensite form. However, while scanning consecutive lines or layers, the printed material undergoes a kind of in-process tempering. In their work, Poirier and Kohli defined a tempering parameter that can consider the combination of both time and temperature in non-isothermal condition like in LPBF process.[71] Figure 7(b) plots the correlation of the tempering parameter and rockwell hardness (HRC) of 4130 steel obtained in conventional manufacturing techniques.[71] This parameter defined not only correlates well with HRC, but also can be linked with material strength and dislocation. We used cooling information and isothermal lines estimated from a single scan process simulation on 4130 steel to establish regions of different level of martensite inclusion described in Fig. 8. SEM images taken in regions (1), (2), and (3) show clearly different microstructures.

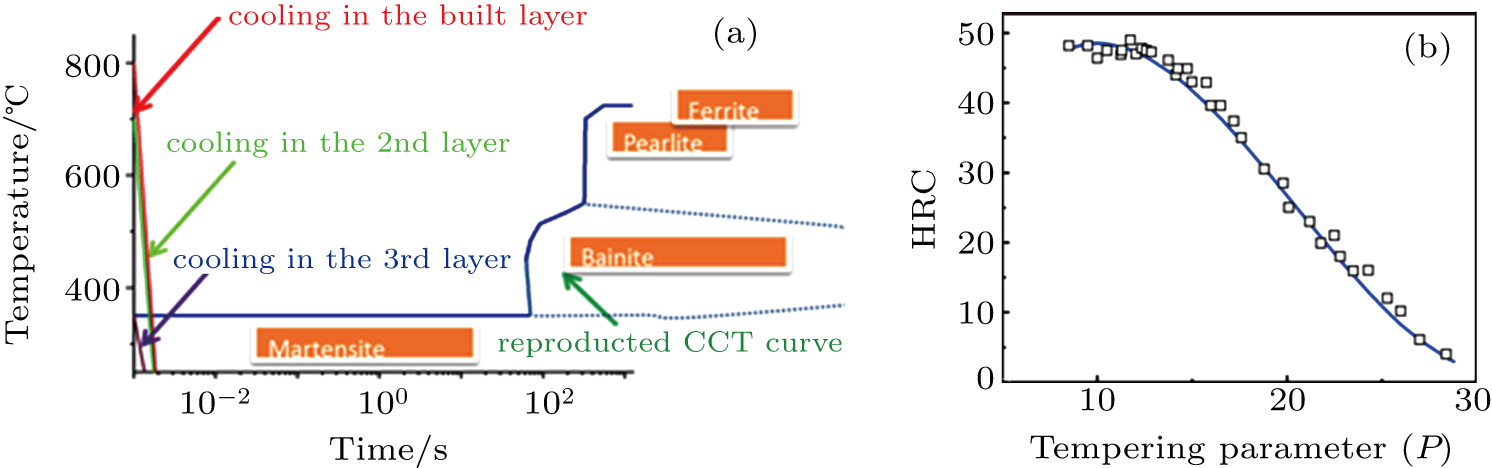Fig. 7. (a) Cooling rate in LPBF process compared to CCT diagram of 4130 steel. (b) Tempering parameter fitting to HRC measurements.
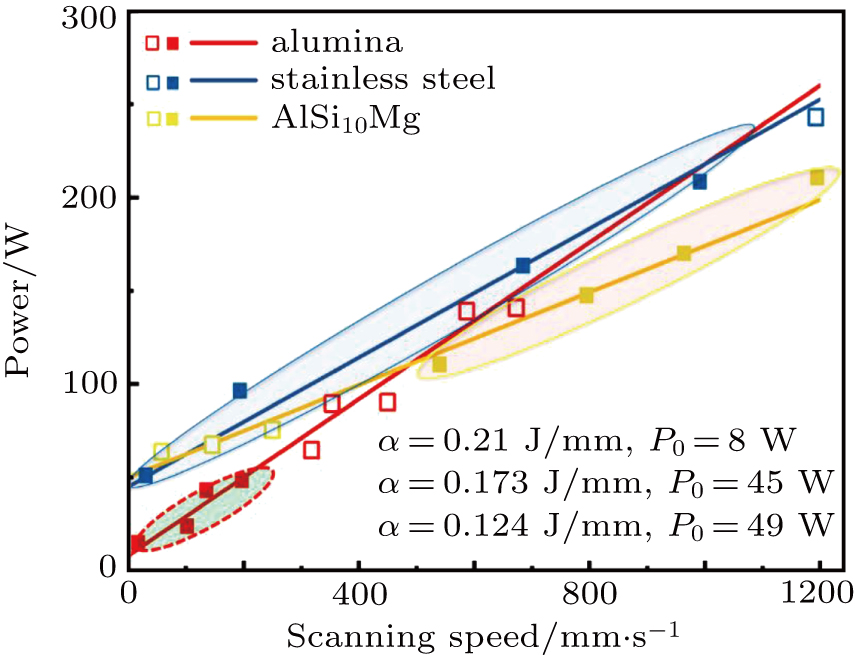
Fig. 8. Regions of different martensite inclusion derived from simulated cooling information (lower) and SEM images of the cross section of a single scan of 4130 steel.
8. Use of energy density formulation

Energy density concept is widely used in LPBF for a quick guide in optimization of parameter combinations. Different formulations available and how experimental observation showed their limitation have been discussed and referenced in introduction section. In our previous work, experimental and simulation results lead to conclusion that, for a given beam size, given layer thickness and hatch distance, the relation between power and scanning speed is rather affine instead of pure linear function. The constant Po is added to account for minimum power needed to melt powder for a static laser being around 45 W for 316L SS.[34] In Fig. 9, simulated combinations of power and scanning speed at a hatch of 120 μm, a beam size of 80 μm and build layer of 30 μm for 316L SS, AlSi10Mg alloy and alumina, are presented. Regions whose combinations are expected to give good quality of melting are highlighted for every material. Due to poor heat conductivity of alumina, fast scanning causes a long but very shallow melt pool. Only slow scan combinations can give good melting. In contrast, due to high thermal conductivity of aluminum alloy, round melt pool can still be achieved even at high scanning speeds. However, due to high thermal conductivity at near room temperature, low power-low speed combinations can not melt aluminum alloy because the heat is easily conducted away.

Fig. 9. Summary of simulated power-scanning speed combinations for good melting quality on basis of modified energy density formulation for different materials.
9. Conclusion and perspectives

In this review we have summarized recent efforts to overcome modeling challenges met at different levels of approximation towards a reliable model that can efficiently simulate LPBF process on basis of finite element codes. Different ways to use the information from simulation of LPBF process are showcased. It is highlighted that, with high fidelity, a computationally efficient model can predict melt pool morphology and temperature history helpful for predetermination of printing quality and properties of printed material. From the overview, our prospective for future research includes:

Improvement of FE techniques to handle more efficiently topological deformation in a multiphase environment like that observed in LPBF process with reasonable computation cost.

Propose a better formulation of energy density metric for quick guide on process parameter combination.

Rely on available simulation and experimental data to build data-based models of LPBF process.

Reference
[1]Petrick I J Simpson T W 2013 Research-Technology Management 56 12
[2]Berman B 2012 Bus. Horiz. 55 155
[3]Liu H Liu M Chang J Su T 2013 Acta Phys. Sin. 62 64705 in Chinese
[4]Hao G Wang X Li X 2015 Chin. Phys. Lett. 32 026103
[5]Jacob G Donmez A Slotwinski J Moylan S 2016 Meas. Sci. Technol. 27 115601
[6]Li N Lü X Weng J 2018 Acta Phys. Sin. 67 057801 in Chinese
[7]Yin P Zhang R Liu Q Hu J Li Y Li N 2013 Chin. Phys. Lett. 30 098104
[8]Khairallah S A Anderson A T Rubenchik A King W E 2016 Acta Mater. 108 36
[9]Matilainen V P Piili H Salminen A Nyrhilä O 2015 Phys. Procedia 78 377
[10]Taheri Andani M Dehghani R Karamooz-Ravari M R Mirzaeifar R Ni J 2017 Mater. Des. 131 460
[11]Semak V Matsunawa A 1997 J. Phys. D. Appl. Phys. 30 2541
[12]Assouroko I Lopez F Witherell P 2016 Proceedings of the Asme International Mechanical Engineering Congress and Exposition 2 UNSP V002T02A068
[13]Fu C H Guo Y B Sealy M P 2014 J. Mater. Proc. Technol. 214 2926
[14]Promoppatum P Yao S C Pistorius P C Rollett A D 2017 Engineering 3 685
[15]Yin J Zhu H Ke L Hu P He C Zhang H Zeng X 2016 Int. J. Adv. Manuf. Technol. 83 1847
[16]Zeng K Pal D Gong H J Patil N Stucker B 2015 Mater. Sci. Technol. 31 945
[17]Boley C D Mitchell S C Rubenchik A M Wu S S Q 2016 Appl. Opt. 55
[18]Gusarov A V Smurov I 2010 Phys. Procedia 5 381
[19]Antony K Arivazhagan N Senthilkumaran K 2014 J. Manuf. Process 16 345
[20]Han Q Setchi R Lacan F Gu D Evans S L 2017 Mater. Sci. Eng. 698 162
[21]Gürtler F J Karg M Leitz K H Schmidt M 2013 Phys. Procedia 41 881
[22]Li Y Gu D 2014 Addit. Manuf. 1 99
[23]Martin A A Calta N P Khairallah S A Wang J Depond P J Fong A Y Thampy V Guss G M Kiss A M Stone K H Tassone C J Nelson Weker J Toney M F van Buuren T Matthews M J 2019 Nat. Commun. 10 1
[24]Zhao C Fezzaa K Cunningham R W Wen H De Carlo F Chen L Rollett A D Sun T 2017 Sci. Rep. 7 1
[25]Escano L I Parab N D Xiong L Guo Q Zhao C Fezzaa K Everhart W Sun T Chen L 2018 Sci. Rep. 8 1
[26]Craeghsa T Clijstersa S Krutha J P Bechmannb F Ebertb M C 2012 Phys. Procedia 39 753
[27]Ye D Zhu K Fuh J Y H Zhang Y Soon H G 2019 Opt. Laser Technol. 111 395
[28]Leung C L A Marussi S Atwood R C Towrie M Withers P J Lee P D 2018 Nat. Commun. 9 1
[29]Guo Q Zhao C Escano L I Young Z Xiong L Fezzaa K Everhart W Brown B Sun T Chen L 2018 Acta Mater. 151 169
[30]Wang D Wu S Fu F Mai S Yang Y Liu Y Song C 2017 Mater. Des. 117 121
[31]Xia M Gu D Yu G Dai D Chen H Shi Q 2017 Int. J. Mach. Tools Manuf. 116 96
[32]Pei W Zhengying W Zhen C Junfeng L Shuzhe Z Jun D 2017 Appl. Phys. 123 540
[33]Klocke F Wagner C Klocke F 2003 CIRP Ann. 52 177
[34]Willy H J Li X Chen Z Herng T S Chang S Ong C Y A Li C Ding J 2018 Mater. Des. 157 24
[35]Mills K C 2002 Woodhead Publishing Series in Metals and Surface Engineering: Recommended Values Thermophysical Properties for Selected Commercial Alloys 13514210.1533/9781845690144.135
[36]Li X Willy H J Chang S Lu W Herng T S Ding J 2018 Mater. Des. 145 1
[37]Dezfoli A R A Hwang W S Huang W C Tsai T W 2017 Sci. Rep. 7 41527
[38]Li X Tan Y H Willy H J Wang P Lu W Cagirici M Ong C Y A Herng T S Ding J 2019 Mater. Des. 178 107881
[39]Wang L Wei Q S Shi Y S Liu J H He W T 2011 Adv. Mater. Res. 233�?35 2844
[40]Campanelli S L Casalino G Contuzzi N Angelastro A Ludovico A D 2014 SPIE 8963 896311
[41]Gong H Rafi K Gu H Janaki Ram G D Starr T Stucker B 2015 Mater. Des. 86 545
[42]Hann D B Iammi J Folkes J 2011 J. Phys. D. Appl. Phys. 44 445401
[43]Prashanth K G Scudino S Maity T Das J Eckert J 2017 Mater. Res. Lett. 5 386
[44]Scipioni Bertoli U Wolfer A J Matthews M J Delplanque J P R Schoenung J M 2017 Mater. Des. 113 331
[45]Barlow A J Maire P H Rider W J Rieben R N Shashkov M J 2016 J. Comput. Phys. 322 603
[46]COMSOL Inc 2017 COMSOL Multiphysics Modeling Softwarehttps://www.comsol.com/
[47]Loh L E Chua C K Yeong W Y Song J Mapar M Sing S L Liu Z H Zhang D Q 2015 Int. J. Heat Mass Transf. 80 288
[48]Xia M Wang P Zhang X H Ge C C 2018 Acta Phys. Sin. 67 170201 in Chinese
[49]Iguchi M Ilegbusi O J 2011 Model. Multiphase Materials Processes: Gas-liquid Systems Berlin Springer 3010010.1007/978-1-4419-7479-2
[50]Yafei S Yongjun T Jing S Dongjie N 2009 Chin. Cont. Decis. Conf. 375610.1109/CCDC.2009.5191721
[51]Sih S S Barlow J W 2004 Part. Sci. Technol. 22 427
[52]Gu D Yuan P 2015 J. Appl. Phys. 118 233109
[53]Dutil Y Rousse D R Ben N Lassue S Zalewski L 2011 Renew. Sustain. Energy Rev. 15 112
[54]Gusarov A V Kovalev E P 2009 Phys. Rev. 80 024202
[55]Bruggeman D A G 1935 Ann. Phys. 416 636
[56]Bruyere V Touvrey C Namy P 2014 Proc. 2014 COMSOL Conf. 1 1https://www.comsol.com/paper/download/199279/touvrey_paper.pdf
[57]Willy H J 2017 Proc. 2017 COMSOL Conf. 1 1https://www.comsol.com/paper/download/504182/tan_paper.pdf
[58]Li Y Gu D 2014 Mater. Des. 63 856
[59]Liu Y Zhang J Pang Z 2018 Opt. Laser Technol. 98 23
[60]Hussein A Hao L Yan C Everson R 2013 Mater. Des. 52 638
[61]Ganeriwala R Zohdi T I 2016 Granular Matter 18 1273https://link.springer.com/article/10.1007/s10035-016-0626-0
[62]Li X Tan W 2016 Proc. 27th Ann. Int. SFF Conf. 1 219https://pdfs.semanticscholar.org/240a/157db00390a045b5f35cb3e7064011237eb2.pdf
[63]Boley C D Khairallah S A Rubenchik A M 2015 Appl. Opt. 54 2477
[64]Bergström D Powell J Kaplan A F H 2007 Appl. Surf. Sci. 253 5017
[65]Moser D Pannala S Murthy J 2015 JOM 67 1194
[66]Yang Y Gu D Dai D Ma C 2018 Mater. & Design 143 12
[67]Gusarov A V Kruth J P 2005 Int. J. Heat Mass Transf. 48 3423
[68]Gusarov A V 2010 Quantum Electron. 40 451
[69]Angle J P Wang Z Dames C Mecartney M L 2013 J. Am. Ceram. Soc. 96 2935
[70]Ma M Wang Z Gao M Zeng X 2015 J. Mater. Process. Technol. 215 142
[71]Gallina D 2011 Eng. Fail. Anal. 18 2250
[72]Hua H Shin J Kim J 2014 J. Fluids Eng. 136 021301
[73]Leitz K H Singer P Plankensteiner A Tabernig B Kestler H Sigl L S 2018 Met. Powder. Rep. 72 332