† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61564002 and 11664005), the Science and Technology Foundation of Guizhou Province, China (Grant No. QKH-[2017]1055), and Guizhou University Talent Foundation (Grant No. GDJHZ-[2015]23).
GaAs multiple concentric nano-ring structures (CNRs) are prepared with multistep crystallization procedures by droplets epitaxy on GaAs (001) to explore the influence of different initial crystallization temperatures on CNRs morphology. Atomic force microscope (AFM) images show that GaAs nanostructures are more likely to form elliptical rings due to diffusion anisotropy. Meanwhile, with the increase of initial crystallization temperature, the inner ring height and density of CNRs are increased, and outer rings are harder to form. In addition, the mechanism of formation of CNRs is discussed by classical nucleation theory and diffusion theory. The method can be used to calculate the diffusion activation energy of gallium atoms (0.7±0.1 eV) on the GaAs (001) surface conveniently.
In nearly a decade, numerous efforts have been devoted to low-dimensional semiconductor nanostructures due to the growing interest in both unique physical properties and their potential application in nanodevices.[1–3] Concentric quantum ring nanostructures make it possible to explore magneto–optical excitation based on Rashba spin–orbit interaction. Concentric quantum ring has a unique dispersion of magnetic field energy level. The energy dispersion of excitons with different radii of ring is different because the total angular momentum of the ground state changes from zero to non-zero by increasing the magnetic field, unlike quantum dots.[4,5] Concentric quantum rings offer the control of effective coupling of direct–indirect excitons, it could pave the way to multiple level states devices with switchable interaction in the research of semiconductor-based quantum computational devices.[6] More and more researchers are attracted to determine the geometry of concentric quantum rings carefully.
To date, many theoretical contributions have been made on the formation of nanostructures, such as nano holes, quantum dot rings, concentric quantum rings, and quantum dots that formed from gallium droplets on GaAs (001).[7] Spirina studied the process of metal droplet formation and motion under the Langmuir evaporation conditions through Monte Carlo simulation.[8] Barseghyan investigated the Josephson effect in quantum structures by performing the numerical renormalization group calculations.[9] However, only a few experimental results on the GaAs concentric quantum rings (CNRs) by droplet epitaxy (DE) are reported, the details of the processes controlling the shapes and sizes of nanostructure have not been systematically investigated yet.[10,11] There still has not been well understood on the influences of crystallization temperature and time on the formation of GaAs CNRs.
In this paper, GaAs multiple concentric nano-ring structures (CNRs) are prepared by multistep crystallization procedures by droplets epitaxy to research the influence of different initial crystallization temperatures on CNRs morphology. The theoretical physical model and experimental results are combined to explore the formation mechanism of CNRs. In addition, the method gives a convenient way to calculate the diffusion activation energy of gallium atoms on the GaAs (001) surface.
The experiments were carried out in a molecular beam epitaxy (MBE) system (Omicron) under ultra-high vacuum (UHV) (4 × 10−9–8 × 10−9 Torr (1 Torr = 1.33322×102 Pa) throughout). The substrates used in experiments were ‘epi-ready’ n-type (Si doped 10−18 cm−3) GaAs (001) wafer. After the oxide desorption at 580 °C, A 1000-nm thick GaAs buffer layer was first grown at a growth rate of 0.3 monolayer (ML)/s and substrate temperature of 560 °C. The GaAs layer was annealed without changing substrate temperature for 40 min to prepare the atomically smooth surface under 9-μTorr As4 beam equivalent pressure (BEP).
To research the formation mechanisms and diffusion anisotropy of multiple structures of GaAs CNRs, the substrate temperature was then decreased to 350 °C and the arsenic valve closed. Subsequently, we performed a sequential four-steps procedure.
The reflection high-energy electron diffraction (RHEED) pattern changes during the every growth experiment, as described in Ref. [12], allowing us to assess the structural evolution of CNRs which happened during the growth. After the above procedure, the morphology of samples was obtained by atomic force microscope (AFM) at room temperature.
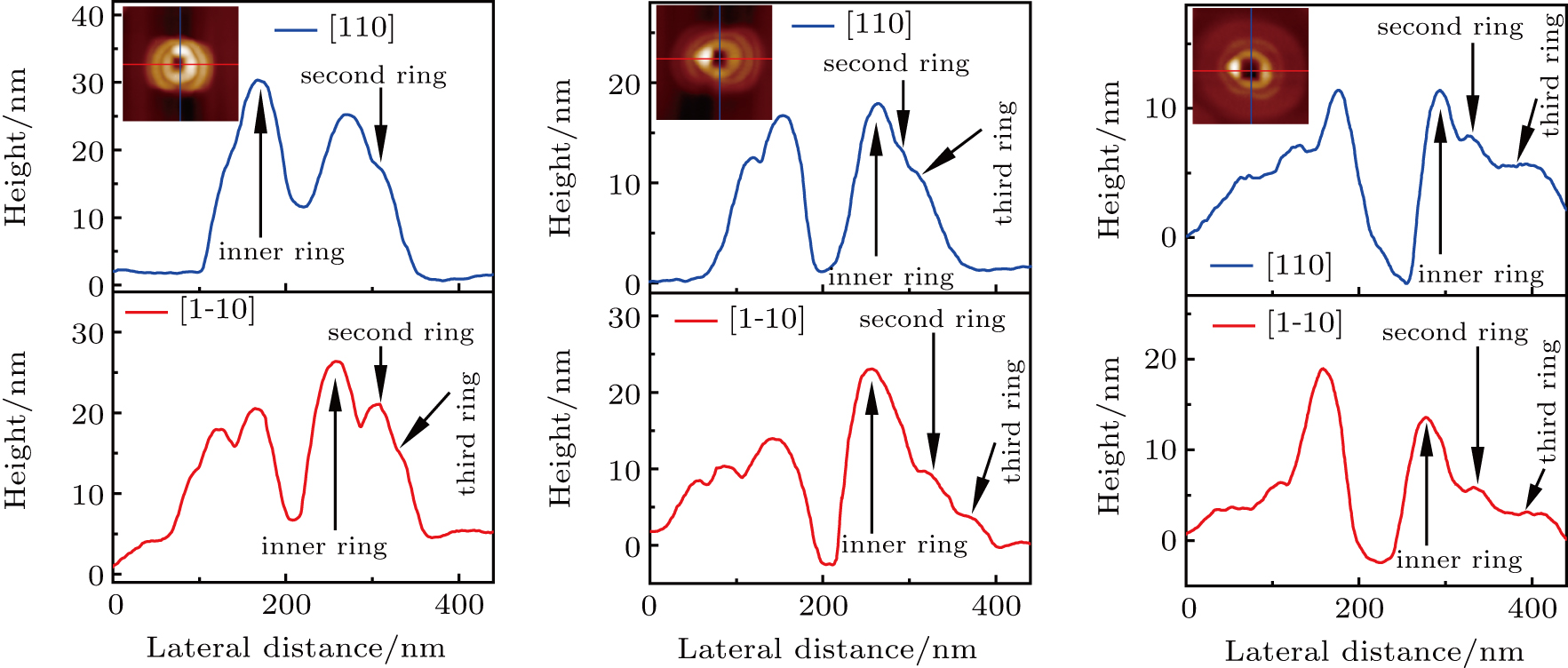
Under the arsenic flux, CNRs evolve starting from gallium droplets to concentric quantum rings at different initial crystallization temperatures according to experimental arrangement in Step 2 (240 °C; 250 °C; 260 °C; 270 °C). The AFM images of CNRs obtained from the deposited droplets after crystallization at different temperature are shown in Figs.
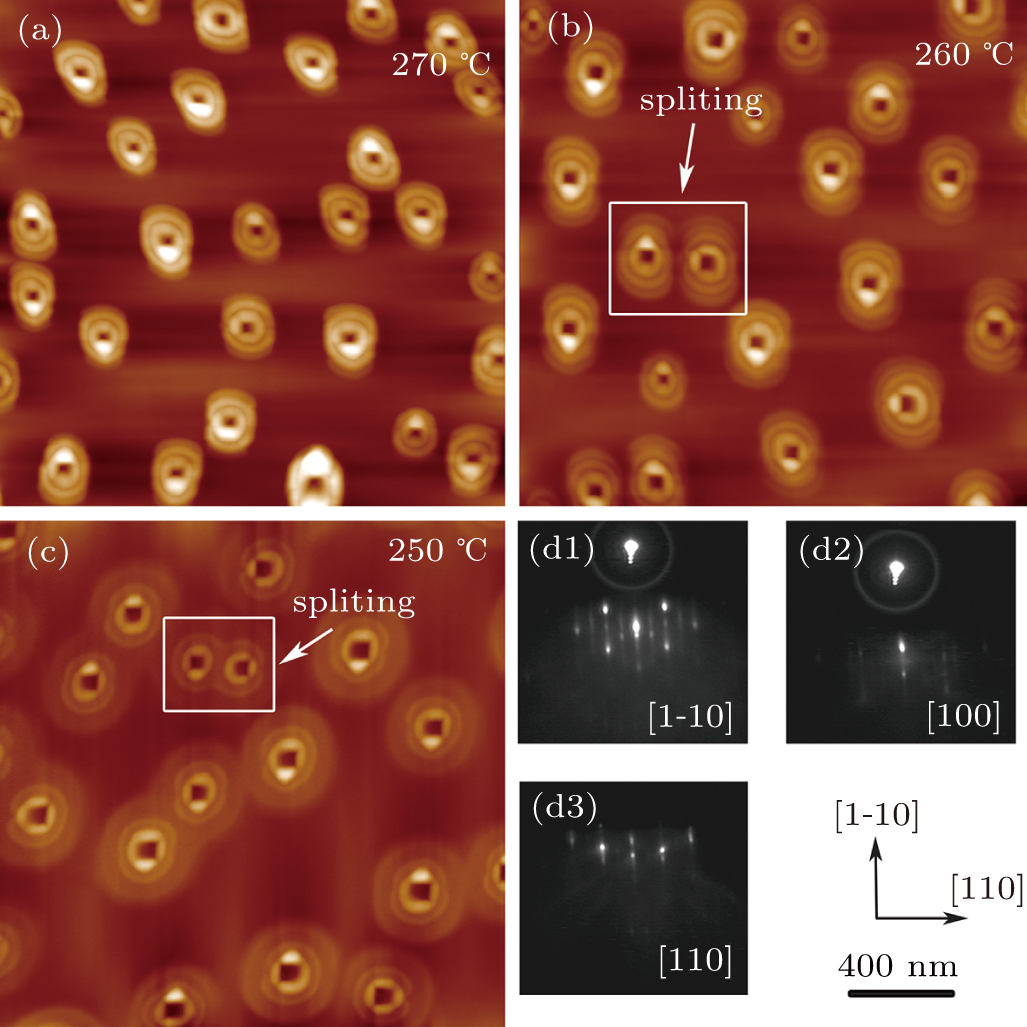 | Fig. 1. AFM images (a)–(c) and RHEED patterns (d1)–(d3) of the samples with different initial crystallization temperatures at Step 2 (270 °C; 260 °C; 250 °C) respectively. |
The RHEED patterns (in panels (d1)–(d3)) show that there is still weak reconstruction on the substrate surface after the crystallization, which indicates that gallium atoms diffused outward and crystalized with arsenic flux in layer by layer growth mode to form rings that kept the reconstruction of substrate.[13] In order to obtain quantitative morphology change information in our experiments, each GaAs CNRs was selected from Figs.
Taking into account the AFM images of samples, we propose a formation mechanism of CNRs based on the arsenic atoms adsorption and diffusion anisotropy of gallium atoms. Figure
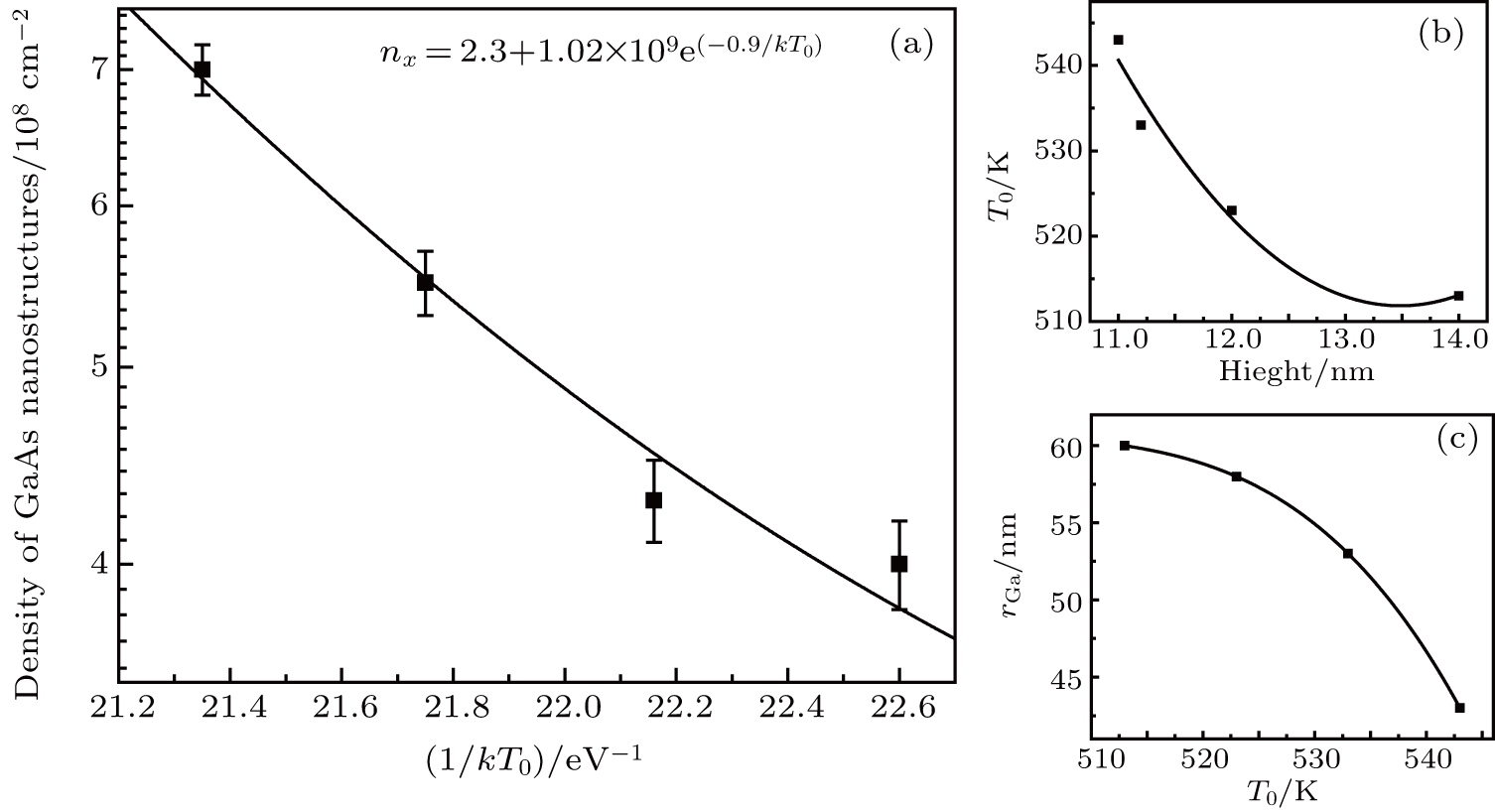
According to nucleation theory by Venables,[14–16] the equations for cluster density (nx) are of the form
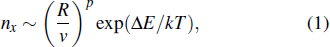
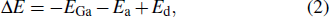
In addition, we measured the average height and radius of the inner ring, statistically averaged the measured results and plotted them, as shown in Figs.
According to Fick law and the growth model of CNRs,[18] we can retrieve the size of diffusion of gallium atoms as follows:
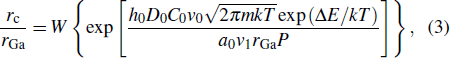
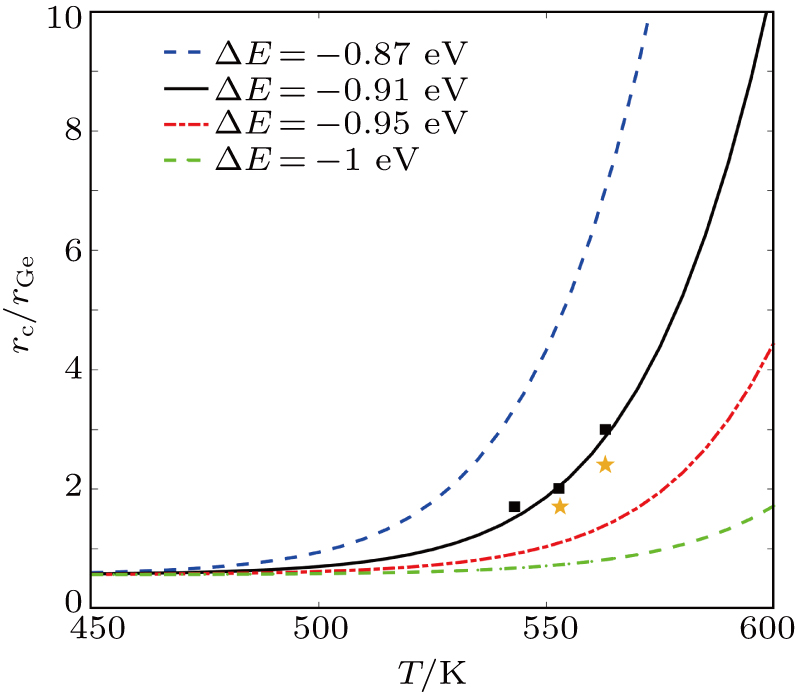 | Fig. 5. The rc/rGa versus crystallization temperature with various ΔE (−0.87 eV; −0.91 eV; −0.95 eV; −1 eV) by Eq. ( |
For this model, we can further discuss the effect of arsenic pressure on outer ring formation. With arsenic pressure as a parameter (ΔE is −0.91 eV), the fitting of the Eq. (
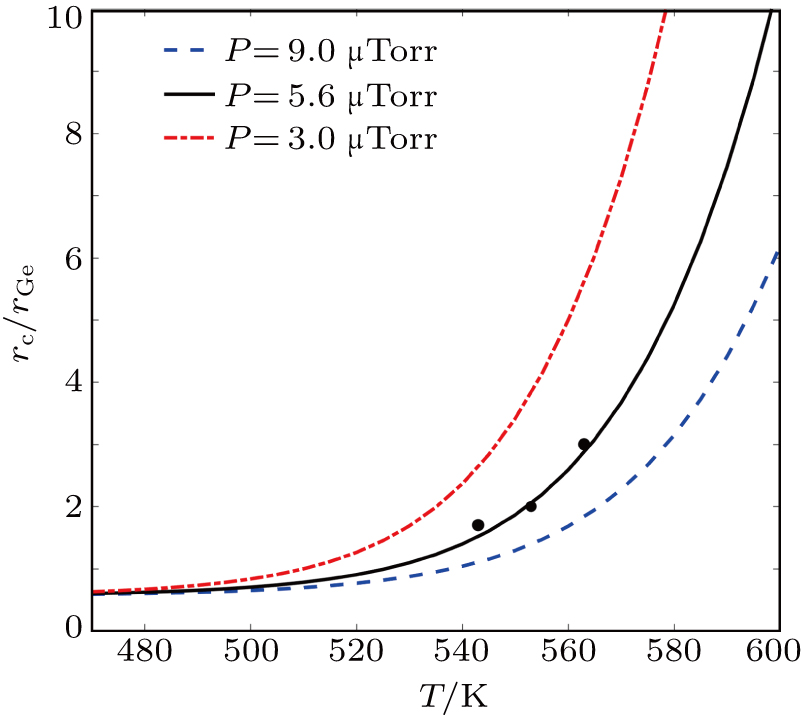 | Fig. 6. rc/rGa versus crystallization temperature with various arsenic pressures (9 μTorr; 5.6 μTorr; 3 μTorr) by Eq. ( |
To confirm the formation mechanism of GaAs CNRs and to generalize the growth model, we extended one more crystallization step performed at different crystallization temperatures by the techniques previously described to realize four concentric nanorings (F-CNRs) grown. 15-MLs gallium is deposited at 350 °C and four subsequent crystallization processes were performed at 240 °C, 270 °C, and 280 °C for 10 s respectively and at 290 °C for 20 min to ensure full crystallization of the F-CNRs. The AFM images and line profile, showing the good rotational symmetry F-CNRs, are observed in Figs.
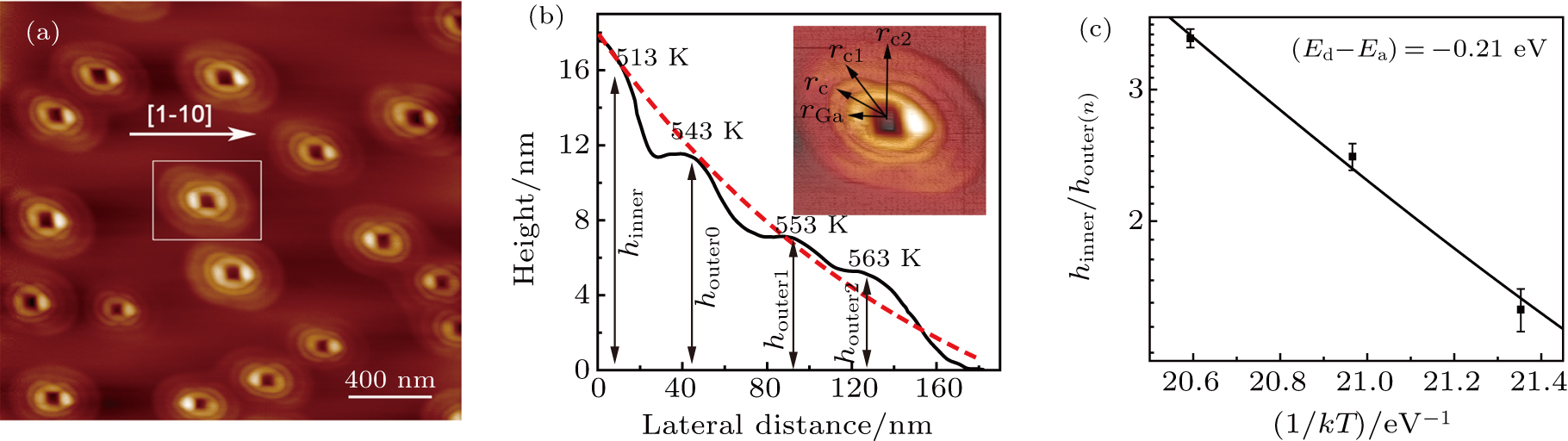 | Fig. 7. (a) AFM image of as-grown sample with four-CNR; (b) half AFM profiles along the [110] direction; (c) hinner/houter(n) versus crystallization temperature. |
We can extend the formula for the relation between the height of the reference outer ring and inner ring in Ref. [19] to a more general case.[19] The ratio between the heights of each layer of outer ring (houter(n)) and inner ring (hinner) could be closely proportional to
| Table 1. Comparation of values in scientific literature for EGa. . |
This result can be further substituted into Eq. (
It should be pointed out that the previous model by Koshiba did not take into account of the time consumed when the temperature rises or drops in the actual experiment, which may lead to the extension of the diffusion distance, and thus may cause a certain error between the result we solved and the theoretical result of Koshiba. Also, the result of our model is an average that ignores the diffusion anisotropy. As the temperature increases, more obvious anisotropy will lead to more and more errors between the experimental and the theoretical results.
In conclusion, the GaAs CNRs were fabricated by droplet epitaxy. We proposed a growth model based on the surface diffusion of gallium atoms at various initial crystallization temperatures and interpreted the growth mechanism on the basis of the morphological evolution of the CNRs and the diffusion of gallium atoms by the model we used. AFM images show that GaAs nanostructures are more likely to form elliptical rings due to diffusion anisotropy. Meanwhile, with the increase of initial crystallization temperature, the inner ring height and density of CNRs increased, and outer rings are harder to form. In addition, the mechanism of the formation of CNRs was discussed by classical nucleation theory and diffusion theory and calculated the diffusion activation energy of gallium atoms (0.7 ± 0.1 eV) on the GaAs (001) surface. The reliable determination of the diffusion activation energy of gallium atoms on GaAs (001) will provide an effective control way to design and fabricated GaAs CNRs.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] |