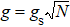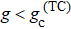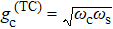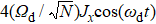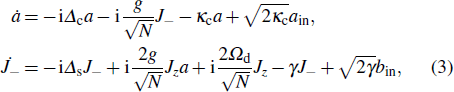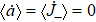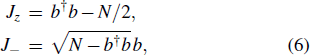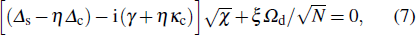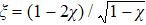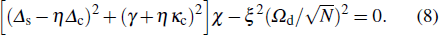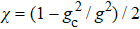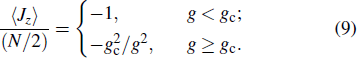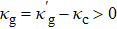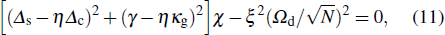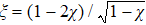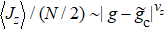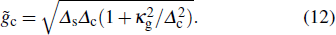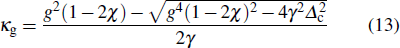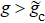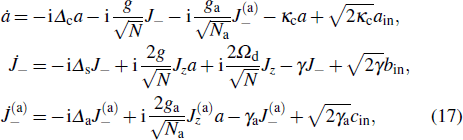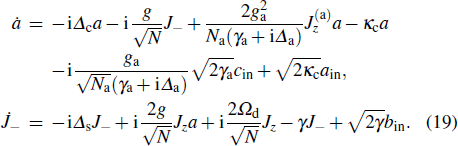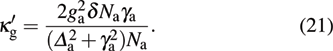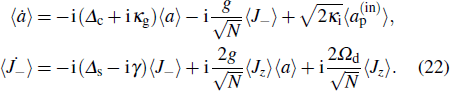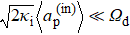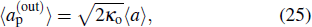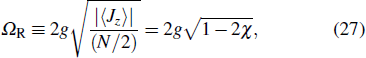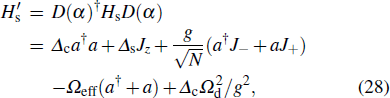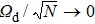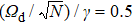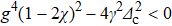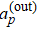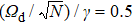1. IntroductionDue to its fundamental importance and potential applications in quantum technologies, quantum phase transition (QPT) in, e.g., the Dicke model has attracted much attention.[1–19] In quantum optics, the Dicke model, which describes the collective behavior of two-level systems (TLSs) interacting with a cavity mode, was first used to study the superradiance.[20] This model includes both rotating and counter-rotating interactions between the TLS ensemble and the cavity mode. In the thermodynamical limit, when continuously varying the strength of the collective interactions, the system undergoes a QPT at a critical coupling strength (equal to the half of the geometric mean of the resonance frequencies of the TLS ensemble and the cavity mode).[21–27] With maller (larger) than the critical coupling strength, the TLS ensemble is in the normal (superradiant) phase. When neglecting the counter-rotating coupling terms via the rotating-wave approximation (RWA),[28] the Dicke model can be reduced to the Tavis–Cummings (TC) model.[29] Similar to the Dicke model, the TC model can also exhibit a QPT, but the corresponding critical coupling strength is twice the critical coupling strength of the Dicke model.[30] However, the very large critical coupling strength (in either the Dicke or TC model) is not accessible in a realistic physical system.
To circumvent this difficulty, the nonequilibrium QPT was theoretically proposed[31–34] and experimentally implemented[35–38] by simulating the superradiant QPT with drive physical systems. For instance, an effective Dicke Hamiltonian was designed by pumping the ensemble of four-level atoms coupled to an optical cavity mode with two drive fields.[31] In this engineered Dicke model, the QPT is controlled by tuning the coupling strength between the TLS ensemble and the cavity mode via varying the drive-field frequencies and intensities. Then, this proposed scheme was implemented using a hybrid system consisting of a Bose–Einstein condensate in a dilute atomic gas and an optical cavity.[35] In addition, by off-resonantly pumping the standard TC model with a drive field, an effective TC Hamiltonian can also be engineered in a rotating frame with respect to the drive field.[34] In the ideal case without decoherence for the system, the driven TC model can have a QPT in the weak drive-field limit, where the experimentally achievable critical coupling strength is equal to the geometric mean of the frequency detunings of both the cavity mode and the TLS ensemble from the drive field. Usually, both cavity mode and TLS ensemble are dissipative. The losses of the cavity mode and the TLS ensemble then greatly obscure the QPT in the TC model,[39–41] as observed in the experiment.[38]
In this paper, we present a scheme to demonstrate the QPT in a biased TC model by including the decoherence of the system. In our proposal, the biased TC model describes a dissipative TLS ensemble pumped by a drive field and coupled to an active cavity mode (instead of a lossy cavity mode[38]). In the rotating frame with respect to the drive field, the effective frequencies of the TLS ensemble and the cavity mode become their frequency detunings from the drive field, respectively. In the limit of a weak drive field, we show that the biased TC model tends to exhibit the QPT owing to the combined actions of the loss and gain of the system. Furthermore, we find that the active cavity can greatly improve the QPT behavior even at a finite strength of the drive field. We also propose to implement the scheme by using an ensemble of nitrogen-vacancy (NV) centers in diamond coupled to an active optical cavity and show that the QPT can be probed by measuring the transmission spectrum of the cavity embedding the TLS ensemble. Our work provides an approach to reduce the adverse effect of the decoherence on the QPT in a biased TC model and can make it promising to experimentally observe the QPT in a realistic system.
2. Dissipative quantum phase transitionFor an ensemble of N TLSs in a cavity, when the coupling between each TLS and the cavity photon is identical, the coupled system can be described in the RWA by a TC model (we set ħ = 1)

where
a† and
a are the creation and annihilation operators of the cavity photon with frequency
ωc,
Jz and
J± ≡
Jx ± i
Jy are the collective operators of the TLS ensemble,
ωs is the transition frequency of each TLS, and
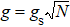
is the collective coupling strength between the TLS ensemble and the cavity photon, with
gs being the TLS–photon coupling strength. Here the RWA applies as the TLS–photon coupling is not beyond the strong-coupling regime.
The TC model has a conserved parity,[25] [HTC,Π] = 0, where Π = exp{iπ(a† a + Jz + N/2)}. In the thermodynamic limit N → + ∞ and without the decoherence of the system, by varying the collective coupling g from the regime 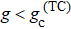 to
to  , where
, where 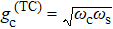 , the system undergoes a QPT from the normal to the super-radiant phase at zero temperature.[21,22] However, it is extremely difficult to experimentally demonstrate this QPT due to the decoherence of the system[39–41] as well as the difficulty in accessing the very large critical coupling strength
, the system undergoes a QPT from the normal to the super-radiant phase at zero temperature.[21,22] However, it is extremely difficult to experimentally demonstrate this QPT due to the decoherence of the system[39–41] as well as the difficulty in accessing the very large critical coupling strength  .
.
To solve these problems, we first reduce the critical coupling strength by applying a field with frequency ωd to drive the TLS ensemble. This corresponds to adding a drive term 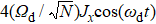 to the Hamiltonian (1), where
to the Hamiltonian (1), where  denotes the collective coupling strength between the drive field and the TLS ensemble, with Ωs being the TLS–field coupling strength. In the rotating frame with respect to this drive field, the Hamiltonian of the system can be converted, in the RWA, to a biased TC model
denotes the collective coupling strength between the drive field and the TLS ensemble, with Ωs being the TLS–field coupling strength. In the rotating frame with respect to this drive field, the Hamiltonian of the system can be converted, in the RWA, to a biased TC model

where
Δc(s) =
ωc(s) −
ωd (> 0) is the frequency detuning of the cavity mode (TLSs) from the drive field. Without the decoherence of the system, this biased TC model tends to exhibit the QPT at

in the limit of weak drive field,
[34] 
, because the Hamiltonian (
2) tends to have the conserved parity (i.e., [
HTC,
Π] = 0) only in this weak drive-field limit. Now,
gc becomes experimentally achievable by just making
Δc and
Δs small via tuning the frequency
ωd of the drive field.
In addition, the QPT can be greatly affected by the decoherence of the system. In fact, for the TC model in Eq. (1), the QPT disappears due to the decoherence of the system.[39–41] In previous studies, the QPT is investigated by diagonalizing the Hamiltonian of the system,[25,34] but it is difficult to diagonalize the Hamiltonian of the system when the decoherence of the system is included. Therefore, we use a quantum Langevin approach[28] to study the QPT in the biased TC model. For the Hamiltonian in Eq. (2), the dynamics of the system is governed by the following quantum Langevin equations:
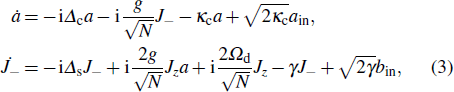
where
κc is the decay rate of the cavity mode,
γ is the damping rate of the TLS ensemble, and
ain (
bin) is the input noise operator acting on the cavity mode (TLS emsemble) which has zero mean value ⟨
ain⟩ = ⟨
bin⟩ = 0.
To study the steady behavior of the system, we write each of the operators a, J−, and Jz as a sum of its mean value and fluctuation, a = ⟨a⟩ + δ a, J− = ⟨J−⟩ + δ J−, and Jz = ⟨Jz⟩ + δ Jz. From Eq. (3), it follows that the mean values ⟨a⟩ and ⟨J−⟩ satisfy

When the system is in the steady state, i.e.,
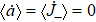
, we obtain from Eq. (
4) that

According to the Holstein–Primakoff transformation,
[42]
we can connect the collective operators
J− and
Jz of the TLSs to the bosonic operators
b and
b†. Under the mean-field approximation, it follows from Eq. (
6) that ⟨
Jz⟩ = ⟨
b† b⟩ −
N/2 and

. Thus, the steady-state equation (
5) becomes
where
χ = ⟨
b† b⟩/
N,
, and

. Multiplying Eq. (
7) by its complex-conjugate counterpart, we obtain an equation for the mean value
χ of the bosonic number opeartor
b†b in the presence of the decoherence
For the ideal case without decoherence, i.e., γ = κc = 0, the above equation is reduced to  . Solving it in the weak drive-field limit
. Solving it in the weak drive-field limit  , we obtain the steady solutions χ = 0 and
, we obtain the steady solutions χ = 0 and 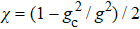 , which correspond to the normal and super-radiant phases for g < gc and g ≥ gc, respectively. Similar to the driven TC model in Ref. [34], in the weak drive-field limit
, which correspond to the normal and super-radiant phases for g < gc and g ≥ gc, respectively. Similar to the driven TC model in Ref. [34], in the weak drive-field limit  and in the absence of decoherence, the biased TC model also tends to exhibit a QPT from the normal to the super-radiant phase at the critical coupling strength g ≡ gc by tuning gc (via the frequency ωd of the drive field) from g < gc to g > gc, with ⟨Jz⟩/(N/2) = 2χ −1 given by
and in the absence of decoherence, the biased TC model also tends to exhibit a QPT from the normal to the super-radiant phase at the critical coupling strength g ≡ gc by tuning gc (via the frequency ωd of the drive field) from g < gc to g > gc, with ⟨Jz⟩/(N/2) = 2χ −1 given by
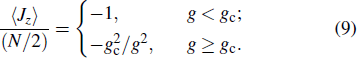
From Eq. (
9), it can be easily obtained that ⟨
Jz⟩/(
N/2) ∼ |
g −
gc|
νz in the vicinity of
g =
gc, with the critical exponent
νz = 1.
[34] However, for a realistic system, both the cavity mode and the TLS ensemble are usually dissipative, i.e.,
γ > 0 and
κc > 0. Even in the weak drive-field limit

, the TLS ensemble tends to always stay in the trivial state with
χ = 0 (i.e., the QPT disappears
[39–41]), because (
Δs −
ηΔc)
2 + (
γ +
ηκc)
2 > 0 in Eq. (
8). At a finite drive-field strength, the QPT is greatly obscured by both the decoherence of the system and the drive field (cf. Fig.
1(a)).
[38]To circumvent this situation, we can harness an active cavity mode with the effective gain rate 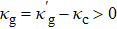 coupled to a dissipative TLS ensemble with damping rate γ, where a gain rate
coupled to a dissipative TLS ensemble with damping rate γ, where a gain rate  is introduced by using a gain medium in the cavity (cf. Section 3). This corresponds to the case with κc in the first equation of Eq. (3) replaced by −κg. In this active-cavity case, equation (3) becomes
is introduced by using a gain medium in the cavity (cf. Section 3). This corresponds to the case with κc in the first equation of Eq. (3) replaced by −κg. In this active-cavity case, equation (3) becomes

Similar to Eq. (
8), the steady-state behavior of the system is now governed by
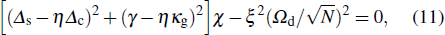
where
χ and
ξ are also given by

and
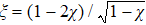
, but

.
With an appropriate gain rate satisfying γ − ηκg = 0, the steady-state equation (11) of the system is also reduced to  , as in the case without decoherence for the system. In the weak drive-field limit
, as in the case without decoherence for the system. In the weak drive-field limit  , the steady-state solution in Eq. (9) can also be obtained in the presence of decoherence and ⟨Jz⟩/(N/2) has the same critical behavior, i.e.,
, the steady-state solution in Eq. (9) can also be obtained in the presence of decoherence and ⟨Jz⟩/(N/2) has the same critical behavior, i.e., 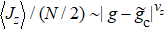 , with νz = 1, but the critical coupling strength becomes
, with νz = 1, but the critical coupling strength becomes
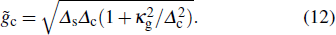
Solving
γ −
ηκg = 0 and ignoring the trivial solution, we have
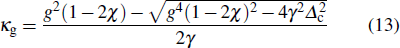
in the region
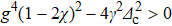
, i.e.,
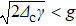
when

, and

when
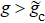
. Obviously, the effective gain rate
κg varies for different critical coupling strengths

, which is experimentally achievable (see Section
3).
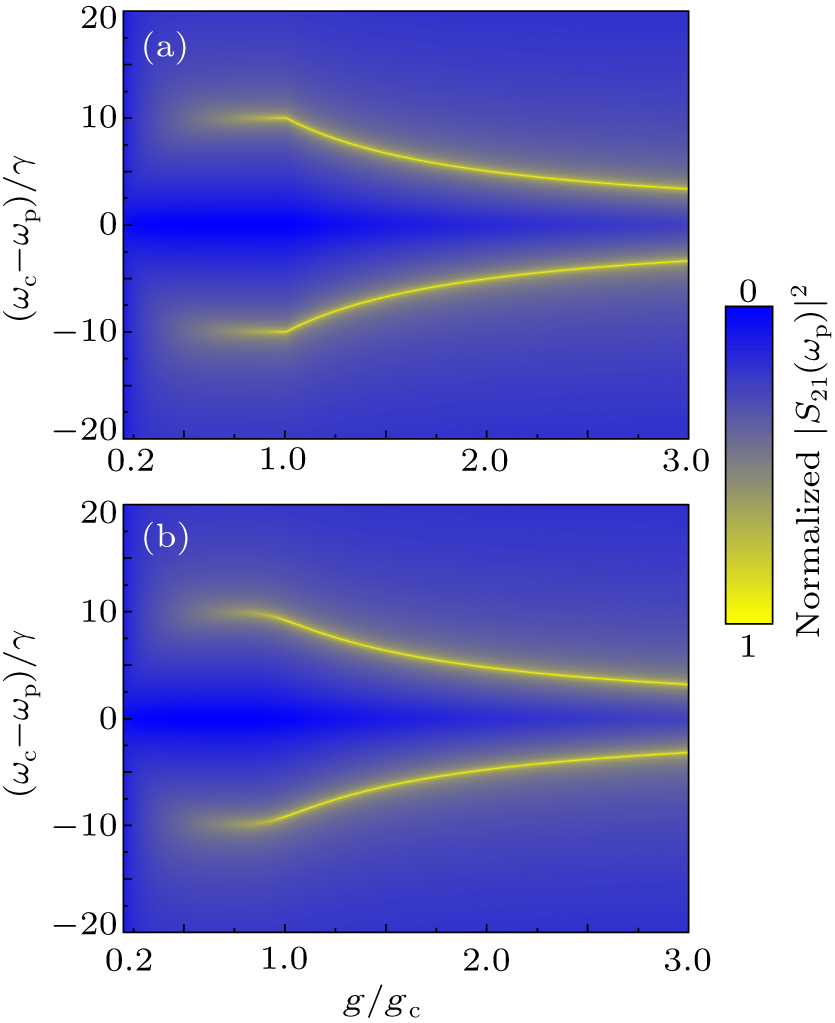
In Fig. 1, we numerically show the QPT in a biased TC model using Eqs. (8) and (11), respectively. Different from Fig. 1(a), no ⟨Jz⟩/(N/2) exists in Fig. 1(b) when g/gc < 0.2 (see the grey region) because  in this region [cf. Eq. (13)]. In the region of 1.2 < g/gc < 3, ⟨Jz⟩/(N/2) gives rise to bistability at a finite drive-field strength [cf. the blue dashed curve in Fig. 1(b)], where the higher and lower branches are stable and the intermediate branch is unstable. When sweeping the coupling strength g/gc rightwards (leftwards), the higher (lower) branch is approachable. Hereafter, we only focus on the higher stable branch of the blue dashed curve in the bistable region, which corresponds to the case of sweeping g/gc rightwards. As expected, for the ideal case of κc = γ = 0, there is the QPT in the weak drive-field limit
in this region [cf. Eq. (13)]. In the region of 1.2 < g/gc < 3, ⟨Jz⟩/(N/2) gives rise to bistability at a finite drive-field strength [cf. the blue dashed curve in Fig. 1(b)], where the higher and lower branches are stable and the intermediate branch is unstable. When sweeping the coupling strength g/gc rightwards (leftwards), the higher (lower) branch is approachable. Hereafter, we only focus on the higher stable branch of the blue dashed curve in the bistable region, which corresponds to the case of sweeping g/gc rightwards. As expected, for the ideal case of κc = γ = 0, there is the QPT in the weak drive-field limit  [see the black solid curve in Fig. 1(a)]. When including the losses of both cavity mode and TLS ensemble, the QPT disappears either in the weak drive-field limit or at a finite drive-field strength [see the red dotted curve and the blue dashed curve in Fig. 1(a)]. Instead of a lossy cavity, if an active cavity is coupled to the lossy TLS ensemble and their gain and loss rates satisfy Eq. (13), the system tends to approach the QPT behavior in the weak drive-field limit, even for the finite drive-field strength in Fig. 1(a) [comparing the red dotted curve and the higher stable branch of the blue dashed curve in Fig. 1(b) with the red dotted line and the blue dashed curve in Fig. 1(a)]. Therefore, an active cavity can much improve the QPT behavior in a biased TC model.
[see the black solid curve in Fig. 1(a)]. When including the losses of both cavity mode and TLS ensemble, the QPT disappears either in the weak drive-field limit or at a finite drive-field strength [see the red dotted curve and the blue dashed curve in Fig. 1(a)]. Instead of a lossy cavity, if an active cavity is coupled to the lossy TLS ensemble and their gain and loss rates satisfy Eq. (13), the system tends to approach the QPT behavior in the weak drive-field limit, even for the finite drive-field strength in Fig. 1(a) [comparing the red dotted curve and the higher stable branch of the blue dashed curve in Fig. 1(b) with the red dotted line and the blue dashed curve in Fig. 1(a)]. Therefore, an active cavity can much improve the QPT behavior in a biased TC model.
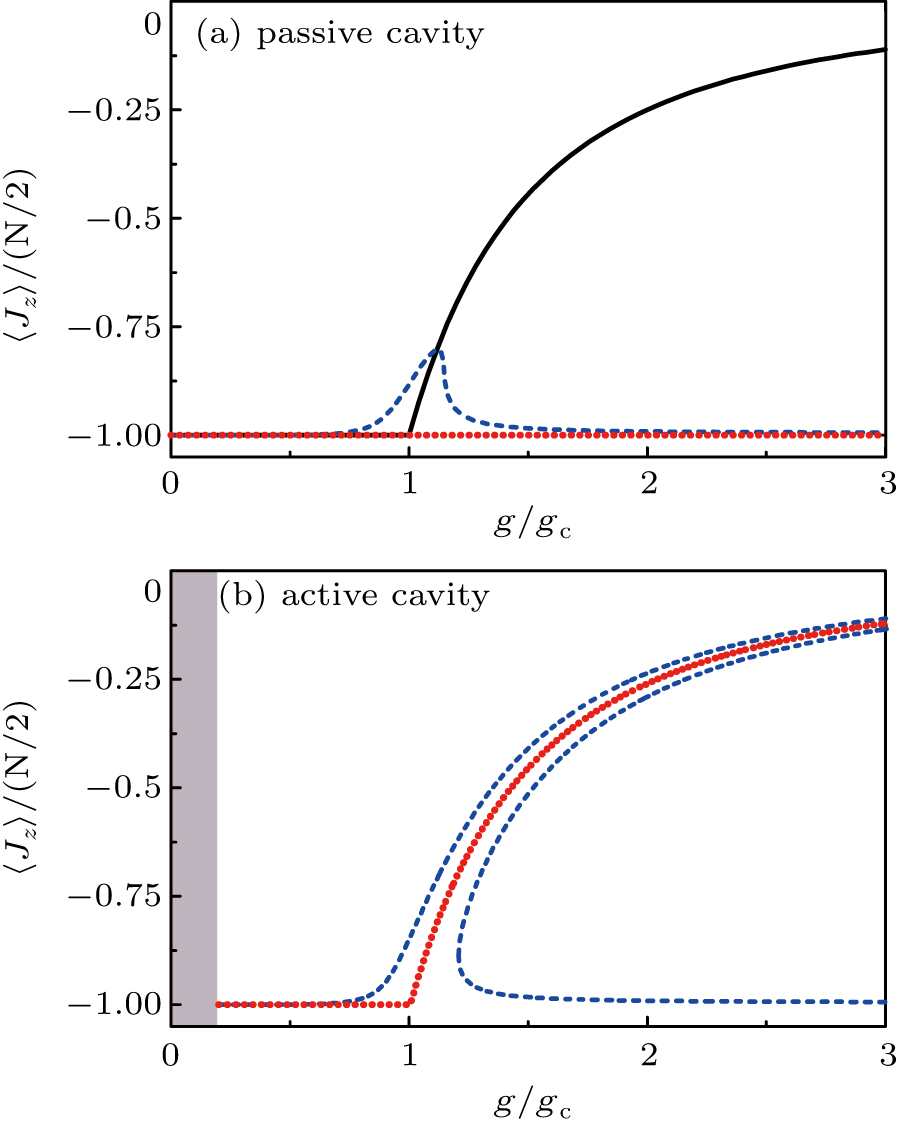
3. Possible implementation using NV centers coupled to an optical cavityThe gain has been widely studied in optical cavities.[43,44] Below we propose to implement our scheme using an ensemble of NV centers in diamond coupled to an active optical whispering-gallery-mode (WGM) cavity,[45–47] where each NV center acts as a TLS with the ground and excited states being 3A2 and 3E of the electronic spin.[48]
In the system proposed, the ensemble of NV centers is driven by an optical field with frequency ωd, and the WGM cavity is made from the silica doped with a gain medium (e.g., rare-earth-metal ions).[43,44] This gain medium can be modeled as an auxiliary spin ensemble with population inversion,[49] as schematically shown in Fig. 2(a). Without the auxiliary spin ensemble, the coupled system is also described by the Hamiltonian Hs in Eq. (2).[50,51] In the rotating frame with respect to the drive field on the NV centers, the Hamiltonian of the auxiliary spin ensemble is

and the interaction Hamiltonian between the auxiliary spin ensemble and the WGM cavity is

where
Δa =
ωa −
ωd is the frequency detuning between the auxiliary spin ensemble (with transition frequency
ωa) and the drive field on the NV centers,

and

are the collective operators of the auxiliary spin ensemble, and
ga is the collective coupling strength between the auxiliary ensemble of
Na spins and the WGM mode. The total Hamiltonian
H =
Hs +
Haux +
Hint of the proposed system in Fig.
2(a) can now be written, in the rotating frame, as

For clearity, we display the energy-level structure in Fig.
2(b) for the above Hamiltonian.
With the auxiliary spin ensemble included, the quantum Langevin equations of the total system are
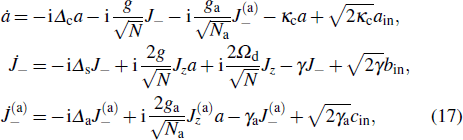
where
γa is the decay rate of the auxiliary spin ensemble, and
cin is the input noise operator of the auxiliary spin ensemble which also has the zero mean value ⟨
cin⟩ = 0. Assuming that the auxiliary spin ensemble is in the steady state, we have

by setting

in the third equation of Eq. (
17). With the above equation, we can eliminate the degree of freedom of
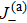
and reduce Eq. (
17) to
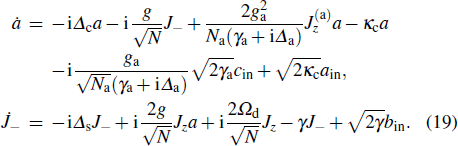
If the population inversion of the auxiliary spin ensemble is denoted as
δ Na (> 0),

. By replacing the operators

and
cin with their expected values
δ Na and 0, respectively, equation (
19) is reduced to the same form as in Eq. (
10), but the auxiliary spin ensemble shifts the frequency of the WGM mode to

where

, with
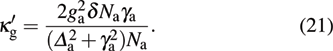
In the experiment, the gain rate

(related to the population inversion
δNa) can be tuned from 0 to, e.g., 450 MHz by varying the amplitude of the pump-laser field acting on the gain medium, while the change of the frequency of the cavity due to the gain medium is very slight.
[52] Without loss of generality, below we neglect the effect of the gain medium on the frequency shift of the WGM mode.
In the experiment, the dissipative QPT can be measured via the transmission spectrum of the active WGM cavity embedding an ensemble of NV centers. When considering the probe field  , it corresponds to adding a probe term
, it corresponds to adding a probe term  to the first equation in Eq. (10), where κi is the decay rate of the cavity mode induced by the input port. Then, from Eq. (10), it follows that
to the first equation in Eq. (10), where κi is the decay rate of the cavity mode induced by the input port. Then, from Eq. (10), it follows that
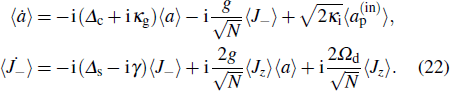
Compared with the drive field on the NV centers, the probe field is usually chosen extremely weak in the spectroscopic measurement,
[53] i.e.,
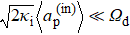
. By performing a Fourier transform on Eq. (
22), we obtain the quantum Langevin equations in the frequency domain

where
ω =
ωp −
ωd is the frequency detuning of the probe field (with frequency
ωp) from the drive field on the NV centers. To avoid the influence of the drive field, the probe field is tuned off-resonance with the drive field (i.e.,
ωp ≠
ωd), so the
δ-function term in Eq. (
23) can be removed. Solving the above equation, we obtain the intra-cavity field

According to the input–output theory,[28] when no input field is applied to the output port, the output field can be written as
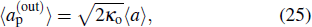
where
κo is the decay rate of the cavity mode induced by the output port. Now, the total decay rate of the cavity mode is
κc =
κi +
κo +
κint, with
κint being the intrinsic decay rate. Combining Eqs. (
24) and (
25), we can derive the transmission coefficient

via the relationship

, where the effective Rabi frequency,
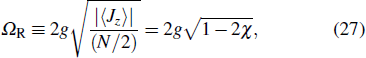
corresponds to the separation between the two Rabi-splitting peaks in the transmission spectrum of the cavity, which can be measured in the experiment.
Using Eqs. (11) and (26), we can simulate the transmission spectrum |S21(ωp)|2 of the active WGM cavity embedding the dissipative ensemble of NV centers. Figures 3(a) and 3(b) show the simulated transmission spectra versus ωc − ωp and g/gc in the weak drive-field limit and at a finite drive-field strength, respectively, where the corresponding ⟨Jz⟩/(N/2) can be found in Fig. 1(b). The maximal values in each transmission spectrum (see the yellow pattern) represent the two Rabi-splitting peaks. At a fixed coupling strength g/gc in the transmission spectrum, ⟨Jz⟩/(N/2) can be obtained from the separation between the two Rabi-splitting peaks [cf. Eq. (27)].
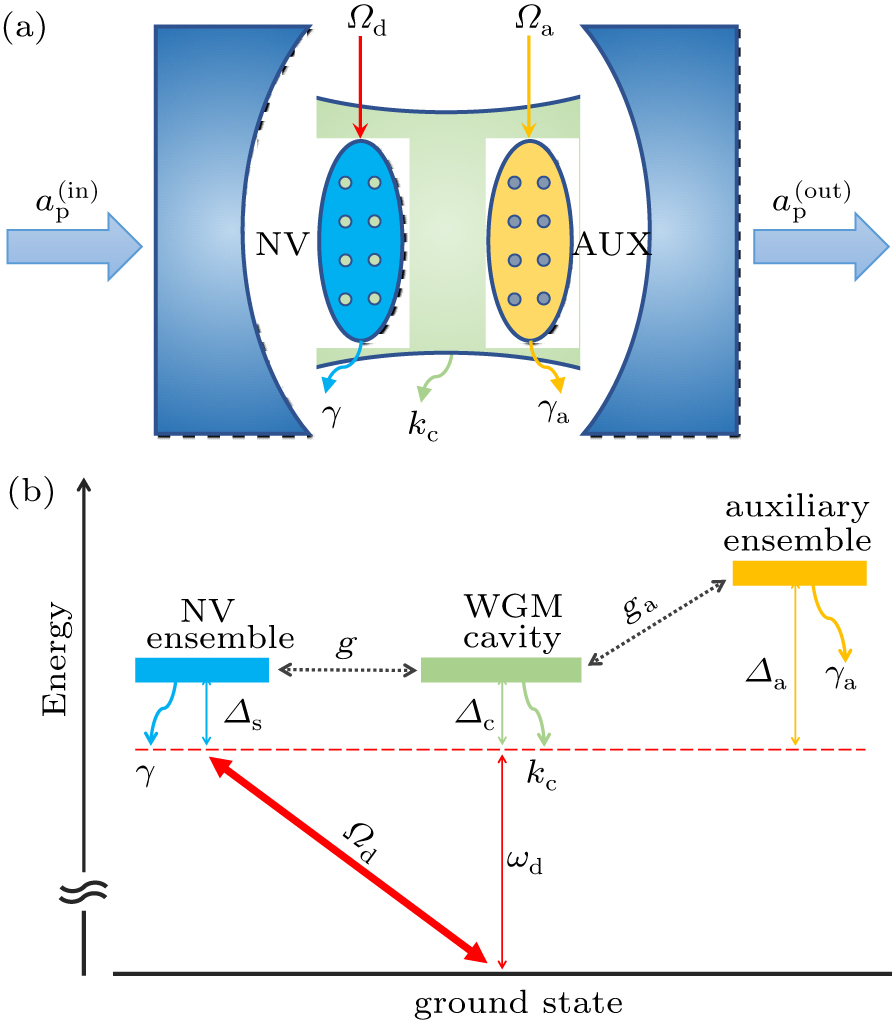
4. Discussion and conclusionsFor a TC model, one can also use a pump field to directly drive the cavity instead of the TLS ensemble.[34] Actually, both cases of driving the cavity and the TLS ensemble are essentially equivalent. Using a unitary transform D(α) = eα a† − α*a (with α = − Ωd/g) on the biased TC model in Eq. (2), we obtain
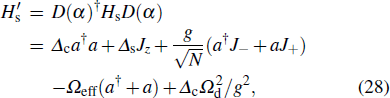
where
Ωeff =
Ωd Δc/
g is the effective Rabi frequency on the cavity mode. Comparing Eq. (
28) with Eq. (
2), we can see that driving the TLS ensemble with a Rabi frequency
Ωd is equivalent to driving the cavity mode with a Rabi frequency
Ωeff. Thus, the conclusions in Sections
2 and
3 are still valid in the case of driving the cavity. For the standard TC model without the decoherence of the system, the occurrence of the superradiant QPT is related to the parity-symmetry breaking.
[30,34] In our considered dissipative situation, however, it is difficult to show the parity-symmetry change of the system when the QPT occurs, because deriving an effective compact Hamiltonian of the system becomes very challenging.
[38–41] In Ref. [
34], it is theoretically shown that in a driven TC model, the QPT can occur in the ideal case without the decoherence of the system. However, the losses of the cavity mode and the TLS ensemble smear out the QPT, as demonstrated in the experiment.
[38] Our scheme circumvents this difficulty and provides a promising approach to experimentally realize the QPT in a biased TC model.
In summary, we have theoretically studied the dissipative QPT in a biased TC model. We propose to couple a dissipative ensemble of TLSs with an active cavity field, where the TLS ensemble is pumped by a drive field. Using a quantum Langevin approach, we demonstrate the existence of QPT in the weak drive-field limit when the loss and gain rates of the system satisfy a certain constraint. Also, we propose to experimentally implement our scheme with a lossy ensemble of NV centers coupled to an active optical cavity and also show that the QPT can be measured using the transmission spectrum of the cavity embedding the TLS ensemble.