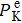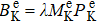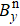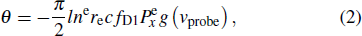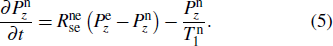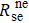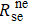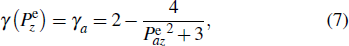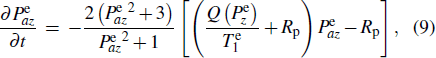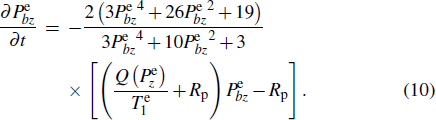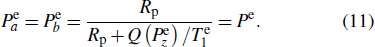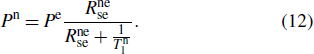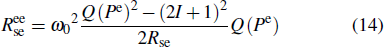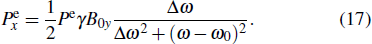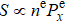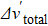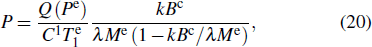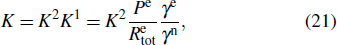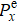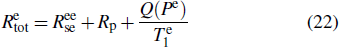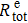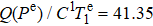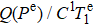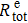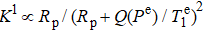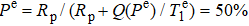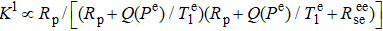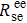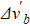Cite this Article
Lu Yan, Zhai Yueyang, Zhang Yong, Fan Wenfeng, Xing Li, Quan Wei. Spin-exchange relaxation of naturally abundant Rb in a K–Rb–21Ne self-compensated atomic comagnetometer. Chinese Physics B, 2020, 29(4): 043204  
Permissions
Spin-exchange relaxation of naturally abundant Rb in a K–Rb–21Ne self-compensated atomic comagnetometer
Lu Yan1, Zhai Yueyang2, 3, 4, Zhang Yong1, Fan Wenfeng1, Xing Li1, Quan Wei2, 3, 4, †
School of Instrumentation Science and Opto-electronics Engineering, Beihang University, Beijing 100191, China
Research Institute of Frontier Science, Beihang University, Beijing 100191, China
Beijing Academy of Quantum Information Sciences, Beijing 100191, China
Beijing Advanced Innovation Center for Big Data-Based Precision Medicine, Beihang University, Beijing 100191, China

 

† Corresponding author. E-mail: quanwei@buaa.edu.cn

Project supported by the National Key R&D Program of China (Grant Nos. 2016YFB0501600 and 2017YFB0503100), the National Natural Science Foundation of China (Grant Nos. 61773043, 61673041, 61721091, and 61703025), and the National Science Fund for Distinguished Young Scholars of China (Grant No. 61925301).

Abstract

The total effective spin-exchange relaxation of naturally abundant Rb in a K–Rb–21Ne comagnetometer is analyzed, and the results show that the coexistence of 87Rb and 85Rb isotopes in the same volume can lead to a large extra spin-exchange broadening compared to pure 87Rb. This broadening mainly comes from the contribution of the equivalent reduction in the Rb spin-exchange rate. On this basis, an approximate relaxation model is proposed and experimentally demonstrated to be more accurate than that from a previous work. This study also provides a method for determining the properties of alkali-metal vapor cells.

PACS: ;32.10.Dk;;32.10.Fn;;32.80.Xx;
Keyword:;comagnetometer;;naturally abundant Rb;;spin-exchange relaxation;;spin polarization;
1. Introduction

The self-compensated atomic comagnetometer first introduced in Ref. [1] uses the unique coupling dynamics of alkali-metal and noble-gas spin ensembles to cancel the external random magnetic field and maintain a high sensitivity to other types of interactions. For example, it has been used in tests of Lorentz and CPT symmetries (the CPT symmetry is a discrete symmetry under charge conjugation C, parity inversion P, and time reversal T)[2,3] and spin-dependent forces.[4–6] Furthermore, this comagnetometer can be exploited as a high-precision gyroscope for rotation sensing.[7–9] For these applications, the fundamental limit on the comagnetometer sensitivity is essential, which can be optimized by suppressing the total relaxation rate of the alkali-metal atoms.[7] Thus, research on the various spin relaxations, especially the relaxation caused by spin-exchange (SE) collisions between the alkali-metal atoms in comagnetometers that use relatively heavy noble-gas atoms, such as 21Ne or 129Xe, is particularly important. In such cases, the classical dipolar field from alkali-metal electron magnetization can be considerably enhanced by the Fermi contact interaction between alkali metal and noble gas pairs, which result in large SE relaxation rates.[8,10]

The relaxations of various mechanisms are similar for alkali-metal atoms with different nuclear spins I, except for that caused by the effect of SE collisions. For alkali-metal atoms with different I, the different effects of SE collisions are mainly reflected in the different precession properties,[11] which further affect their polarizations and SE relaxations. Recently, many studies on the self-compensated atomic comagnetometer using naturally abundant Rb (72.2% 85Rb with I = 5/2 and 27.8% 87Rb with I = 3/2) as a spin source[12–15] and studies using 85Rb and 87Rb isotopes in the same volume as the working material for other applications, such as the anomalous long-range spin-mass couplings of the proton[16] and the magnetic resonance affected by the SE of two Rb isotopes,[17] have been performed. However, no detailed studies on SE relaxation considering the effect of two Rb isotopes coexisting in the same volume have been presented.

In this work, based on a K–Rb–21Ne comagnetometer, the pumping process of naturally abundant Rb considering the different effects of SE collisions of each individual isotope on their precession properties is derived, and the result shows that the two isotopes can achieve the same equilibrium spin polarization, although different amounts of time are required. Then, the total effective SE relaxation of naturally abundant Rb is analyzed, and the result shows that the coexistence of 87Rb and 85Rb isotopes in the same volume can lead to a large extra SE broadening compared to the case of using pure 87Rb isotope, which is mainly attributed to the decrease in the effective SE rate of Rb atoms. Based on this analysis, an approximation model is proposed, in which the total effective SE relaxation rate of naturally abundant Rb is assumed to be equal to that of the contained 87Rb isotope. Finally, by comparison with experimental results, this model is proven to be more accurate than the model used in a previous study,[8] in which all naturally abundant Rb atoms were treated as 85Rb atoms.

2. Theoretical analysis
2.1. Operation principle

In a self-compensated atomic comagnetometer, to suppress the relaxation due to SE collisions between alkali-metal atoms, a high-density alkali-metal vapor is required,[11] while for the case of single alkali-metal species, this vapor also results in an optically thick medium, in which case the strong absorption of the pump light produces a significant polarization inhomogeneity in the cell and imposes a limit on the optical pumping efficiency.[18] In this study, the K–Rb hybrid pumping technique[2,18] is utilized in a K–Rb–21Ne comagnetometer to overcome this difficulty. The low-density K atoms, which are optically thin, are first polarized in the z-direction (see Fig. 1) by a circularly polarized pump light. Then, through SE interactions, the high-density Rb atoms are pumped by K atoms, and the 21Ne atoms are hyperpolarized by Rb atoms.[2] After a period of time, K, Rb, and 21Ne reach their respective polarization equilibria 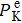, , and Pn. Because the classical dipolar fields from the alkali-metal electron and noble-gas nuclear magnetizations are enhanced by the Fermi contact hyperfine interactions between K–21Ne and Rb–21Ne, the corresponding effective magnetic fields are 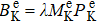, , and Bn = λ Mn Pn, respectively[7] (, , and Mn are the magnetizations corresponding to full spin polarizations). In a spherical cell, λ = 8πκ0/3, where κ0 is the enhancement factor. For K–21Ne and Rb–21Ne pairs, the values of κ0 are approximately 31 and 36, respectively.[20] The density ratio of K to Rb is typically on the order of 10−2. In addition, the K and Rb atoms are in spin-temperature equilibrium and have the same polarization because the SE rate between K and Rb is extremely large (exceeding 106 s−1 at typical densities).[21] Then, the effective magnetic field experienced by 21Ne atoms is two orders of magnitude smaller than . The alkali-metal and noble-gas spin ensembles are coupled through one species precessing in the effective magnetic field of the other. Therefore, the coupling between 21Ne atoms and alkali-metal atoms is dominated by the Rb–21Ne pair, and the coupling between K and 21Ne can be safely ignored. Furthermore, in a K–Rb–21Ne comagnetometer, only Rb atoms are detected by the probe light used to monitor the change in the 21Ne nuclear magnetization and provide the output signal, while K atoms are not detected and are mainly responsible for the effective pumping. In conclusion, the K–Rb–21Ne comagnetometer can be simply represented by the Rb–21Ne comagnetometer.[2,21]

Fig. 1. Intuitive model of the operation principle: (a) Rb and 21Ne achieve polarization equilibrium, then the comagnetometer is set to the self-compensated state with Bz = −B2c = −(Bn + Be); (b) when there is a rotation rate input Ωy, the Rb electron spins are quickly repolarized, while the 21Ne nuclear spins remain oriented with respect to an inertial frame; (c) under the torque of magnetic field Bz on 21Ne nuclear spins, Pn and, accordingly, Bn rotate around the z-axis, resulting in a y-component of the nuclear magnetic field ; (d) under the torque of magnetic field on Rb electron spins, Pe rotates and projects onto the x-axis. Then, the x-component is detected by the linearly polarized probe light.

To visually describe the operation principle, an intuitive model is shown in Fig. 1. Here we take rotation sensing as an example. Figure 1(a) shows the equilibrium polarizations Pe and Pn and the corresponding effective magnetic fields Be and Bn for Rb and 21Ne spin ensembles, respectively. In general, the comagnetometer works in the self-compensated state as follows:[1] , where Bz is the applied magnetic field in the z-direction, and Bc is the compensation point. The comagnetometer can use the unique coupling dynamics of alkali-metal and noble-gas spin ensembles to suppress external magnetic field disturbance in this state.[1] Thus, this is the operating state of the comagnetometer. If there is a rotation rate input Ωy, as shown in Fig. 1(b), then the Rb electron spins will be quickly repolarized, while the 21Ne nuclear spins remain oriented with respect to an inertial frame.[19] Under the torque of magnetic field Bz on 21Ne nuclear spins, as shown in Fig. 1(c), Pn and, accordingly, Bn rotate around the z-axis, resulting in a y-component of the nuclear magnetic field 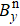, which is experienced by Rb atoms. In Fig. 1(d), under the torque of magnetic field on Rb electron spins, Pe rotates and projects onto the x-axis. In this way, Rb atomic spins can sensitively detect , i.e., the x-component of Rb polarization changes with , which generates a linear correlation between and Ωy,[8]

After a linearly polarized probe beam passes through the Rb vapor cell, the polarization plane of the probe beam rotates to an angle[22]

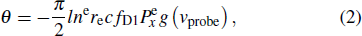
which is proportional to both the Rb density ne and the polarization component . The probe light is modulated by a photoelastic modulator (PEM), the photoelectric conversion signal of the photodetector (PD) is demodulated by a lock-in amplifier, and the first harmonic is recorded as the ultimate output signal[23]

which is proportional to the optical rotation angle θ. The output signal is then linearly correlated with the input rotation, and the rotation can be measured.

2.2. Equilibrium spin polarization

The spin evolutions of the coupled Rb and 21Ne spin ensembles in a K–Rb–21Ne comagnetometer can be described by a set of Bloch equations.[6,24] Without any field or rotation input, the Bloch equations in the z-direction are given by

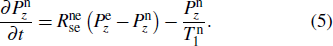
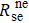
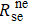
Here Rp is the K–Rb hybrid optical pumping rate, is the SE rate from Rb to 21Ne atoms, and and are the longitudinal relaxation times of the Rb electron spin and the 21Ne nuclear spin (excluding contributions from Rp and ), respectively. is the nuclear slowing-down factor that depends on the nuclear spin I and the polarization of Rb, and for the case of fast SE collisions between Rb atoms in this study, it is expressed as[11]

For an alkali-metal isotope with I = 3/2, the dimensionless gyromagnetic ratio is given by

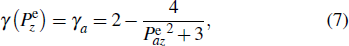
and for an alkali-metal isotope with I = 5/2,

Here the subscripts a and b are used to indicate 87Rb with Ia = 3/2 and 85Rb with Ib = 5/2, respectively.

When using naturally abundant Rb, the different effects of the SE collisions of each individual isotope on their precession properties need to be considered, which is reflected in the fact that they have different . Substituting Eqs. (6), (7), and (8) into Eq. (4), the pumping process of the two isotopes can be described as

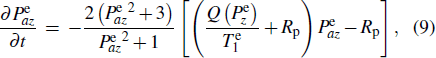
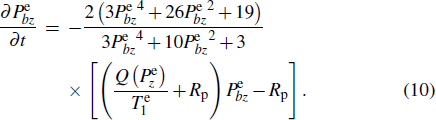
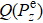
Here the pumping rate Rp and the longitudinal relaxation rate of the 87Rb isotope are assumed to be identical to those of the 85Rb isotope because they occupy the same volume with nearly the same collisional environment (the factors for enhancing the relaxation of wall collisions[25] are different for these isotopes, but this small rate can be neglected for simplicity). Solving Eqs. (9) and (10), the equilibrium spin polarizations of the 87Rb and 85Rb isotopes are given by

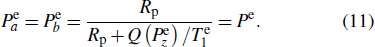
Although the simulation results show that the times required for the two isotopes to reach equilibrium are different, they achieve the same equilibrium spin polarization Pe, which can be used to represent their total equilibrium spin polarization. Additionally, when considering the SE interactions between 85Rb and 87Rb isotopes, because the SE cross-section between 85Rb and 87Rb is 1.7 × 10−14 cm2[26] and the SE rate can reach 105 s−1 at typical densities, the 85Rb and 87Rb isotopes are in spin-temperature equilibrium and can maintain the same polarization. Solving Eq. (5), the equilibrium spin polarization Pn of 21Ne is

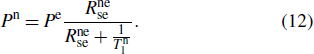
Combining the self-compensation state condition and Eq. (12) gives

Here the constant k is determined in this work from the measurement of Bc based on magnetic field zeroing and the measurement of Be based on the fastest decay of the coupled spin ensembles under the step magnetic field By.[8]

2.3. Spin-exchange relaxation analysis of naturally abundant rubidium

When an SE collision between two atoms occurs, the singlet and triplet states of the dimer formed during the collision have different energies, the singlet and triplet amplitudes evolve at different rates, thus the spin states of the two atoms may change.[27] The total angular momentum of the colliding pair is conserved after the collision, and each individual atom has a probability of switching hyperfine levels. Because the gyromagnetic ratios in the two ground-state hyperfine levels have opposite signs, the spin precession direction of a single atom switches with every SE collision, which leads to dephasing in the spin precession of the ensemble. For the case of SE collisions of the same species, the SE mechanism contributes to the transverse relaxation without affecting the longitudinal component; in the limit case in which the rate of SE collisions Rse is much larger than the Larmor frequency ωL = γeB, the atoms lock into a net precession at a slower rate ω0 in the direction of the F = I + 1/2 state (fast SE regime[11]) because this hyperfine level has a larger statistical weight, and the SE relaxation rate can be expressed as[28,29]

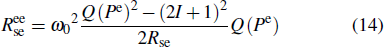
in the low polarization limit. Here the SE rate Rse is given by

where σ and are the SE cross-section and the relative velocity between the pairs of alkali-metal atoms, respectively, and the slower rate ω0 is given by ω0 = γeB/Q(Pe), with γe being the gyromagnetic ratio of a bare electron and B the magnetic field experienced by the alkali-metal atoms. The previous experimental study in Ref. [11] showed that for arbitrary Rb polarization at a low magnetic field of less than approximately 100 nT, Eq. (14) still holds. In this work, the magnetic fields experienced by Rb at different pump light intensities range from 4 to 82 nT, and thus, we can use Eq. (14) for theoretical analysis.

In a vapor cell with naturally abundant Rb, SE collisions also occur between different Rb isotopes. The nuclear spins and hyperfine structures of 87Rb and 85Rb are quite different, and thus, they cannot be treated as one species. SE collisions between different Rb isotopes can shift 85Rb to a higher frequency and 87Rb to a lower frequency, as indicated in Ref. [16], while this effect was ignored in that work, and only the intraisotope interaction was considered. In this study, we also ignore this effect, not only because it has a minor effect on the atomic precession frequency but also because we infer that it does not significantly affect the coherence of the atomic ensemble of each individual isotope. For SE relaxation under the fast SE regime, coherence of the atomic ensemble is the most essential aspect,[22] and it cannot be well achieved by different isotopes with such different precession frequencies, as shown in Fig. 2(c). Therefore, the SE relaxation of each isotope will be considered separately in the following analysis.

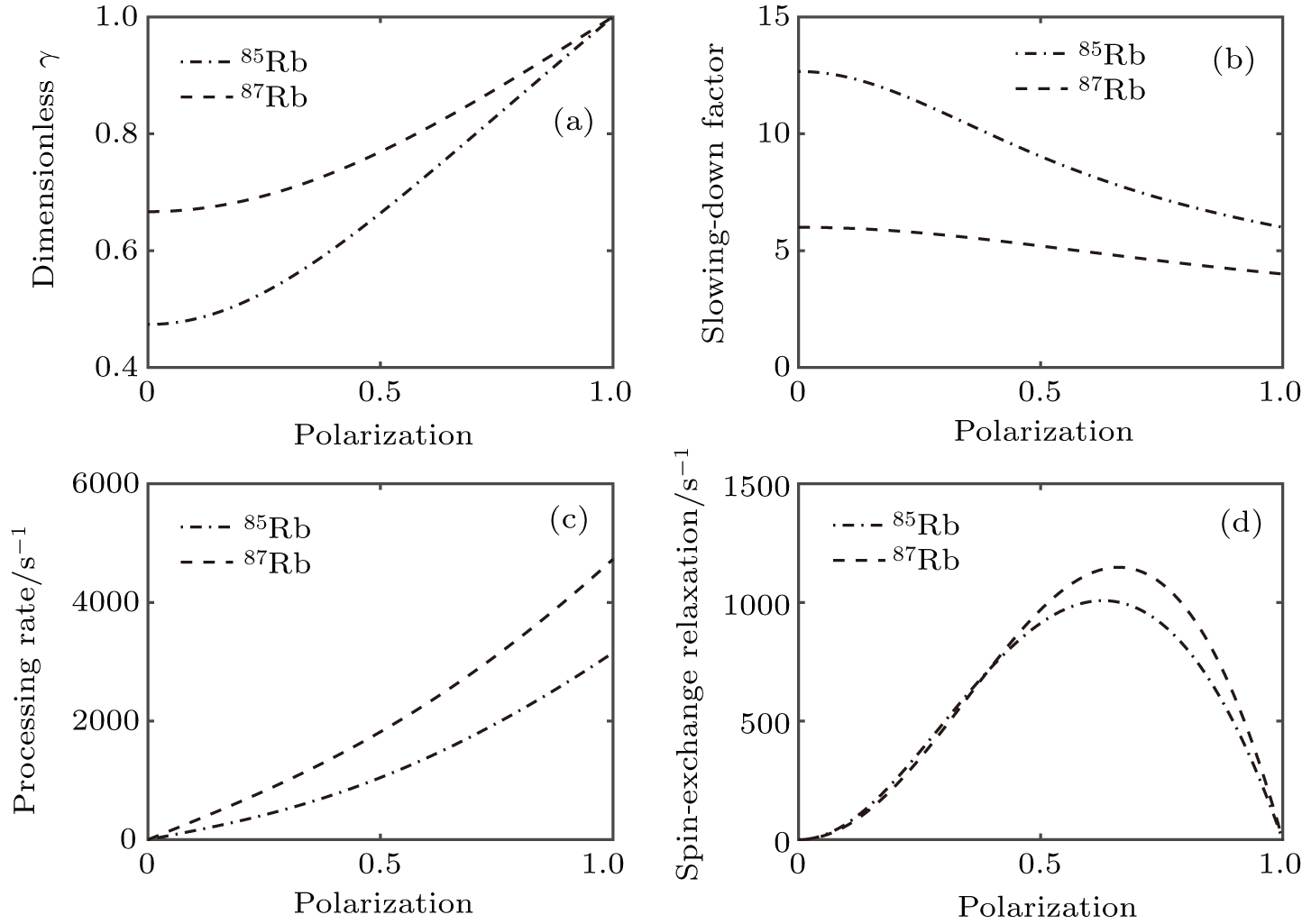
Fig. 2. Simulations for comparison of the various parameters associated with the SE relaxation between the 87Rb and 85Rb isotopes contained in naturally abundant Rb in the same vapor cell. (a) Dimensionless gyromagnetic ratios γ(Pe); (b) slowing-down factors Q(Pe); (c) precession rates ω0; (d) simulated SE relaxation rates in a naturally abundant Rb vapor cell obtained using the densities na = 27.8% × ne and nb = 72.2% × ne for 87Rb and 85Rb, respectively, where ne = 3.831 × 1014 cm−3 is the total Rb vapor density measured during the cell preparation process.

Based on the fact that the two Rb isotopes precess in a common magnetic field equal to −Be (Bz + Bn = −Be), various parameters associated with are simulated and compared between the two isotopes. Figures 2(a), 2(b), and 2(c) show the dimensionless gyromagnetic ratios γ(Pe), slowing-down factors Q(Pe), and precession rates ω0, respectively. These parameters are all different for the two isotopes. Figure 2(d) shows the simulated in a naturally abundant Rb vapor cell obtained using the densities na = 27.8% × ne and nb = 72.2% × ne for 87Rb and 85Rb, respectively, where ne = 3.831 × 1014 cm−3 is the total Rb vapor density measured during the cell preparation process. Using Eq. (15), the calculated Rse values for the two isotopes with SE cross-section σ = 1.9 × 10−14 cm2[30,31] and vapor temperature T = 461 K are Rase = 9.8 × 104 s−1 and Rbse = 2.5 × 105 s−1, respectively.

For the derivation of the total effective of naturally abundant Rb, both the precession rates ω0 and relaxation rates of the two isotopes should be considered. Similar to the magnetic resonance response in an alkali-metal atomic magnetometer,[32] when a cosine oscillating magnetic field By = B0y cos (ω t) is applied, the response is given by

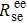
Here the linewidth is Δω = 1/T2 with the transverse relaxation time T2 corresponding to the contribution from SE relaxation . Equation (16) includes the sum of two Lorentzian curves centered at frequencies ±ω0. Because the resonance frequency ω0 is larger than the linewidth Δω, the counterpropagating response centered at −ω0 can be approximately ignored[33] to simplify Eq. (16) to

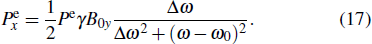
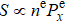
According to Eqs. (2) and (3), the output signal obeys . Then, at a certain Pe, using Eq. (17), we have the total resonance absorption signal of naturally abundant Rb,

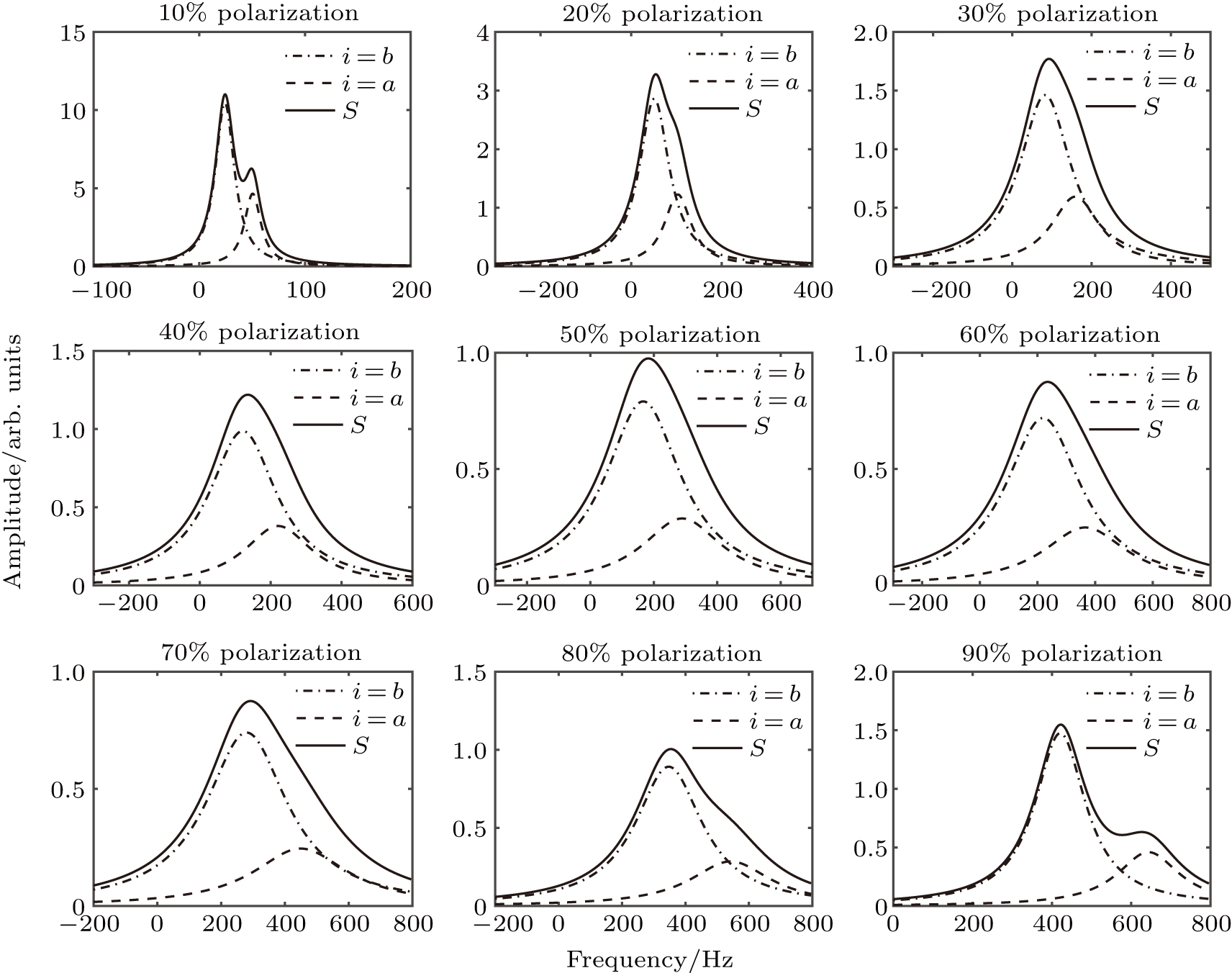
because the two isotopes both participate in the optical probing process and contribute to the output signal. Here the linewidth due to SE broadening is , the resonance frequency is νi0 = ωi0/2π, and h is a constant that is irrelevant to our analysis. From the half width at half maximum (HWHM) of Eq. (18), the total effective SE relaxation of naturally abundant Rb can be estimated. In Fig. 3, the theoretical results based on Eq. (18) are shown, where the solid lines are the total effective SE relaxation rates, and the dashed and dashed-dotted lines correspond to the first and second terms in Eq. (18), respectively.

Fig. 3. Theoretical results of the SE relaxation rates of naturally abundant Rb at different Rb polarizations. The solid lines are the total effective SE relaxation rates; the dashed and dashed-dotted lines correspond to the first and second terms in Eq. (18), respectively.

We find that the absorption curves are distorted due to the difference in the resonance frequencies νa0 and νb0, especially when Δνi is relatively small compared to |νa0 − νb0|. Figure 3 shows that we can obtain the total effective SE relaxation of naturally abundant Rb from the HWHM of magnetic resonance absorption lines within the polarization range of 20% to 80%, and the result is shown by Δνtotal in Fig. 4(a) (black triangles). Here in comparison with the case of using pure 87Rb in a K–Rb–21Ne comagnetometer, we analyze the effect of the coexistence of the two isotopes 87Rb and 85Rb in the same volume on the SE broadening of Rb when using naturally abundant Rb. We choose pure 87Rb for the comparison because its SE relaxation rate is smaller than that of pure 85Rb at arbitrary Rb polarization, as shown by (green triangles) and (purple triangles) in Fig. 4(a), respectively.

Fig. 4. Theoretical results of SE broadening linewidths of magnetic resonance absorption lines. (a) Δνtotal is the linewidth for using naturally abundant Rb, is the linewidth for the assumption that the difference in the resonance frequencies between the two isotopes is zero, Δνa is the linewidth for the assumption that the other isotope 85Rb does not exist in naturally abundant Rb, is the linewidth for using pure 87Rb, and is the linewidth for using pure 85Rb. (b) is the extra broadening of naturally abundant Rb compared to the case of pure 87Rb, is the extra broadening of naturally abundant Rb caused by the reduction in the effective Rb SE rate, and is the extra broadening of naturally abundant Rb caused by the difference in the resonance frequencies of the two isotopes.

In Fig. 4(b), the difference (black diamonds) shows that the linewidth of naturally abundant Rb is considerably broadened compared to the case of using pure 87Rb, which can be attributed to the following reasons: (1) The linewidths due to SE broadening of the two isotopes are different. (2) The resonance frequencies of the two isotopes are different. (3) The fast SE regime is only applicable to a single isotope, and the effective Rb density is only the density of a single Rb isotope contained in naturally abundant Rb; thus, the effective SE rate decreases, leading to large SE broadening. Because the difference in the SE relaxation rates between the two Rb isotopes is small, as shown in Fig. 2(d), the influence of the first factor mentioned above is minor, and we mainly consider the influence of the latter two factors.

Figure 4(a) also shows the theoretical results of the total linewidth 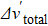(red circles) under the assumption that the difference in the resonance frequencies between the two isotopes is zero and the linewidth Δνa of 87Rb (blue squares) under the assumption that the other isotope 85Rb does not exist in naturally abundant Rb. The calculated (blue squares) and (red circles) in Fig. 4(b) represent the extra broadenings of naturally abundant Rb caused by the difference in the resonance frequencies of the two isotopes and by the reduction in the effective Rb SE rate, respectively. We can see that the large extra broadening of naturally abundant Rb compared to the case of pure 87Rb mainly comes from the contribution of the equivalent reduction in the Rb SE rate, which accounts for approximately 80% of the total extra broadening at a typical Rb polarization of 50%. Therefore, our subsequent work focuses on this dominant factor and ignores the secondary contribution from the different resonance frequencies of the two isotopes, which accounts for approximately 20%.

For further study, we approximate Δνtotal in terms of Δνa, i.e., we assume that the total effective SE relaxation rate of naturally abundant Rb is equal to that of the contained 87Rb isotope. Then, we have

which is referred to as the 87Rb model in this text. Because only the effect of intraisotope SE collisions is considered, this model corresponds to an equivalent decrease in the Rb vapor density ne, which decreases the effective SE rate to Rase = 9.8 × 10−4 s−1.

This approximation model is obviously more accurate than that in a previous study (see in Fig. 4(a)).[8] For verification, the most direct method is to compare experimental results of the SE relaxation with the above theoretical results, but no method to directly measure the SE relaxation currently exists. In this work, we first substitute the 87Rb model into the expression of the scale factor K, which is related to various relaxations of Rb, and fit the experimental results of the Bc ∼ K relationship; then, we calculate the total Rb relaxation rates using the obtained fitting parameters. Finally, we measure the total Rb relaxation rates using two methods (the traditional zero-field resonance line method and the low frequency Bx modulation method[8]) and compare the measured results with the calculated results.

2.4. Theoretical formulas

To determine the various parameters in the comagnetometer, several theoretical formulas are indispensable for fitting the experimental data. From Eq. (11), we have

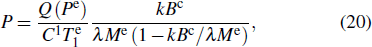
where P is the pump light intensity, and C1 = Rp/P is the optical pumping coefficient, which is a constant.

The scale factor K of the comagnetometer is expressed as

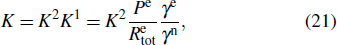
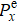
where K2 is the factor that converts into the output voltage signal S by the PEM detection system, γn is the gyromagnetic ratio of the 21Ne nucleus, and

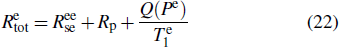
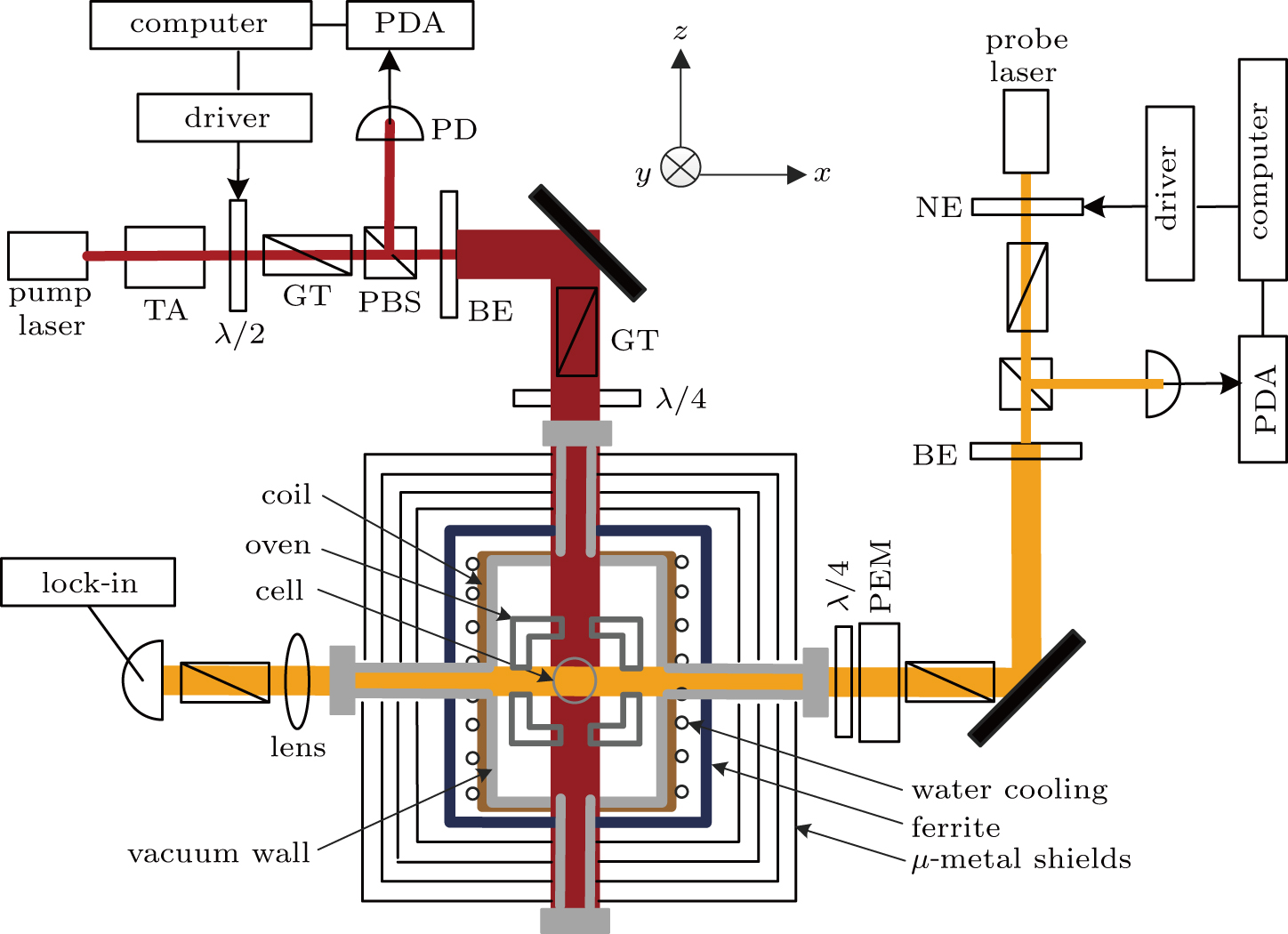
is the total Rb relaxation rate.[28]

3. Experimental setup and procedure

A schematic of the experimental setup is shown in Fig. 5, which is similar to previous apparatuses.[12,35] The comagnetometer includes a spherical aluminosilicate glass vapor cell with a diameter of 14 mm that contains a small droplet of K–Rb mixture with naturally abundant Rb, approximately 2000 Torr 21Ne gas (70% isotope enriched) and approximately 50 Torr N2 gas for quenching. An oven composed of an AC electrical heater system pasted on a boron nitride ceramic is utilized to heat the cell. For thermal insulation, the oven is in a closed vacuum environment, achieved by turbo molecular pumps. To attenuate the ambient magnetic field, four layers of μ-metal magnetic field shields and a layer of a ferrite barrel[36] are utilized around the vacuum wall, and the residual magnetic field is further compensated for by a set of three-axis Helmholtz coils;[37] thus, the magnetic field noise is suppressed. For cooling of the vacuum wall, a water jacket is utilized, and the temperature of the magnetic field shield is sufficiently reduced. The electron spin of K atoms is polarized along the z-axis by the circularly polarized pump light, which is produced by an external cavity diode laser (ECDL) and amplified by a tapered amplifier (TA). The wavelength of the pump light is tuned to the D1 resonance of K. The Gaussian-shaped pump light beam is expanded by a beam expander (BE), and the relatively uniform light intensity area is set to approximately 14 mm × 14 mm using a rectangular aperture to fully cover the vapor cell. The x-component of the Rb polarization is measured by the linearly polarized probe light along the x-axis generated by a distributed feedback (DFB) laser, with a wavelength that is 0.4 nm from the absorption center of the Rb D1 line. The power densities of the pump light and the probe light are stabilized by an electrically controlled half-wave plate and a noise eater, respectively. A PEM modulates the probe light with a frequency of 50 kHz and an amplitude of 0.08 rad. The photoelectric conversion signal of the PD is demodulated by a lock-in amplifier, and the first harmonic is recorded as the ultimate output signal.[23]

Fig. 5. Experimental setup of the K–Rb–21Ne comagnetometer (not to scale). PDA, photodiode amplifier; PD, photodetector; TA, tapered amplifier; GT, Glan–Thompson polarizer; PBS, polarization beam splitter; BE, beam expander; NE, noise eater; PEM, photoelastic modulator.

In this experiment, the temperature of the naturally abundant Rb vapor cell is set to 461 K, and a series of parameters, such as the compensation point Bc, scale factor K and total relaxation rate of Rb atoms, are measured at various pump light intensities. First, the three components of the magnetic field are zeroed before the experiment to achieve the magnetic field self-compensation state, and the compensation field Bc in the z-direction is recorded. Then, the Rb magnetic field Be is measured, and the relationship is fitted using Eq. (13) to obtain k. Next, the Bc ∼ P relationship is fitted using Eq. (20) to obtain λ Me and . Finally, the scale factor K and the total relaxation rate 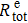are measured using low frequency Bx modulation method, and the Bc ∼ K relationship is fitted using Eq. (21) to obtain C1 and K2. Thus, the theoretical values of the total Rb relaxation rates at various pump light intensities can be calculated using Eq. (22) and compared with the experimental results.

4. Experimental results and discussion

From the fitting of the Bc ∼ Be and Bc ∼ P relationships, as shown in Figs. 6(a) and 6(b), respectively, k = 0.22, 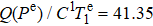mW/cm2, and λ Me = 107.5 nT are obtained. The derived Rb vapor density (from λ Me) ne = 3.876 × 1014 cm−3 agrees well with the value of 3.831 × 1014 cm−3 determined during the filling process of cell preparation. Fitting the relationship between Bc and K, as shown in Fig. 7(a), we have C1 = 32.77 s−1 · mW−1 · cm2 and K2 = 26.11 s· V · nT−1. Substituting the above fitting parameters into Eq. (22), we obtain the theoretical values of the total Rb relaxation rates at various compensation points, as shown in Fig. 7(b) (black line), which are generally consistent with the experimental results of both the traditional method (blue triangles) and the low frequency Bx modulation method[34] (purple diamonds). The Rb polarizations derived from 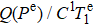are also shown for reference in Fig. 7(c). Combined with the Rb polarization, we can conclude that the 87Rb model is a good approximation in the polarization range of 18%–77% (due to the limitation of the maximum output power of the pump laser in this experiment, the Rb polarization cannot exceed 77%), which corresponds to the applicable range of the theoretical results: 20%–80%. The relatively large deviation between the traditional results and the theoretical values is attributed to the traditional measurement being affected by the magnetic field gradient. Such inaccuracy also exists in the measurement of the scale factor K by the traditional method in a previous study.[35] For an approximate model of the SE relaxation of naturally abundant Rb, the effective SE rate Rse is the most essential aspect, which is 9.8 × 104 s−1 in the 87Rb model. By changing Rse, refitting the Bc ∼ K relationship and recalculating the total Rb relaxation rates, we find that any change in Rse causes a deviation from the experimental result. The red dashed line in Fig. 7(b) is an example with Rse = 3.5 × 105 s−1, corresponding to the approximation in a previous study,[8] in which all naturally abundant Rb atoms are treated as 85Rb atoms (see in Fig. 4(a)). Thus, the 87Rb model is proven to be a more accurate approximation.

Fig. 6. (a) Fitting result of the Bc ∼ Be relationship; (b) fitting result of the Bc ∼ P relationship.
Fig. 7. (a) Fitting result of the Bc ∼ K relationship; (b) comparison between theoretical and experimental results of the total relaxation rate of naturally abundant Rb: the blue triangles and purple diamonds are the measured by the traditional method and low frequency Bx modulation method, respectively, and the black line and red dashed line are calculated using the parameters obtained from fitting the Bc ∼ K relationship with the 87Rb model and the previous approximation in Ref. [8], respectively; (c) Rb polarization.

The polarization validity range of approximately 20–80% of the theoretical results includes the polarizations of nearly 50%, which we are concerned about. The comagnetometer has the maximum signal at nearly 50% polarization of Rb electrons. As shown in Fig. 7, the scale factor is the largest at the compensation point Bc = 235 nT, where the Rb polarization is 49%. Unlike the atomic magnetometer operating in the spin-exchange-relaxation-free (SERF) regime,[22] the maximum signal does not necessarily correspond to 50% electron polarization. In an SERF atomic magnetometer, the SE relaxation does not need to be considered, and the scale factor obeys 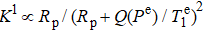. By solving ∂ K1/∂ Rp = 0, we can obtain , and thus, we have . 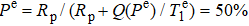In the K–Rb–21Ne comagnetometer, the nonzero SE relaxation rate caused by the relatively large Rb magnetic field is not negligible and should be included in the scale factor K1 as 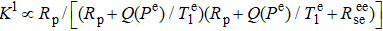. Because is related to Pe and Rp, the solution at the peak of the K curve is not as simple as above. However, the simulation results under different typical experimental conditions show that the solution is within the range of approximately 40%–60%, which is still safely included in the validity range of the theoretical results.

5. Conclusions

In this study, based on a K–Rb–21Ne comagnetometer, we have derived the equilibrium spin polarization of naturally abundant Rb considering the different effects of SE collisions of each individual isotope on their precession properties, and the result shows that although the times required to reach equilibrium for 87Rb and 85Rb are different, these isotopes can reach the same equilibrium spin polarization. Then, we analyze the total effective SE relaxation of naturally abundant Rb and demonstrate that the coexistence of the 87Rb and 85Rb isotopes in the same volume can lead to a large extra SE broadening compared to the case of the pure 87Rb isotope, for which the decrease in the effective SE rate of Rb atoms accounts for approximately 80% and the difference in the resonance frequency of the two isotopes accounts for approximately 20%. Based on this analysis, we propose an approximation model in which we assume that the total effective SE relaxation rate of naturally abundant Rb is equal to that of the contained 87Rb isotope. This model is experimentally proven to be more accurate than the model in a previous study in which all naturally abundant Rb atoms are treated as 85Rb atoms.

The large extra SE broadening demonstrated in this work emphasizes the necessity of using pure 87Rb for improving the sensitivity of the comagnetometer, although naturally abundant Rb is relatively more accessible. The consistency between the 87Rb model and the experimental results indicates the reasonableness of ignoring the minor effect of interisotope SE collisions on the atomic precession frequency for simplicity and considering the SE relaxation of each individual isotope separately in the fast SE regime, which implies that this regime only exists in the single species atomic system. This study is useful for relaxation-related research in which two alkali-metal isotopes coexist in the same volume and provides a method to obtain the properties of the alkali-metal vapor cell, including the spin relaxation rates, spin polarizations and atomic densities.

Reference
[1] Kornack T W Romalis M V 2002 Phys. Rev. Lett. 89 253002
[2] Smiciklas M Brown J M Cheuk L W Smullin S J Romalis M V 2011 Phys. Rev. Lett. 107 171604
[3] Allmendinger F Heil W Karpuk S Kilian W Scharth A Schmidt U Schnabel A Sobolev Yu Tullney K 2014 Phys. Rev. Lett. 112 110801
[4] Bulatowicz M Griffith R Larsen M Mirijanian J Fu C B Smith E Snow W M Yan H Walker T G 2013 Phys. Rev. Lett. 111 102001
[5] Terrano W A Adelberger E G Lee J G Heckel B R 2015 Phys. Rev. Lett. 115 201801
[6] Ji W Chen Y Fu C Ding M Fang J Xiao Z Wei K Yan H 2018 Phys. Rev. Lett. 121 261803
[7] Kornack T W Ghosh R K Romalis M V 2005 Phys. Rev. Lett. 95 230801
[8] Chen Y Quan W Zou S Lu Y Duan L Li Y Zhang H Ding M Fang J 2016 Sci. Rep. 6 36547
[9] Jiang L Quan W Li R Duan L Fan W Wang Z Liu F Xing L Fang J 2017 Phys. Rev. 95 062103
[10] Limes M E Sheng D Romalis M V 2018 Phys. Rev. Lett. 120 033401
[11] Savukov I M Romalis M V 2005 Phys. Rev. 71 023405
[12] Chen Y Quan W Duan L Lu Y Jiang L Fang J 2016 Phys. Rev. 94 052705
[13] Li R Quan W Fan W Xing L Fang J 2017 Sens. Actuat A-Phys. 266 130
[14] Jiang L Quan W Li R Fan W Liu F Qin J Wan S Fang J 2018 Appl. Phys. Lett. 112 054103
[15] Fan W Quan W Zhang W Xing L Liu G 2019 IEEE Access 7 28574
[16] Kimball D F J Lacey I Valdez J Swiatlowski J Rios C Peregrina-Ramirez R Montcrieffe C Kremer J Dudley J Sanchez C 2013 Ann. Phys. (Berlin) 525 514
[17] Dmitriev S P Dovator N A Kartoshkin V A Klementiev G V 2018 J. Phys.: Conf. Ser. 1135 012052
[18] Romalis M V 2010 Phys. Rev. Lett. 105 243001
[19] Brown J M 2011 A New Limit on Lorentz- and CPT-Violating Neutron Spin Interactions Using a K–3He Comagnetometer PhD dissertation Princeton Princeton university
[20] Ghosh R K Romalis M V 2010 Phys. Rev. 81 043415
[21] Quan W Wei K Zhao T Li H Zhai Y 2019 Phys. Rev. 100 012118
[22] Seltzer S J 2008 Developments in alkali-metal atomic magnetometry PhD dissertation Princeton Princeton university
[23] Duan L Fang J Li R Jiang L Ding M Wang W 2015 Opt. Express 23 32481
[24] Bloch F 1946 Phys. Rev. 70 460
[25] Chi H Quan W Zhang J Zhao L Fang J 2020 Appl. Surf. Sci. 501 143897
[26] Jarrett S M 1964 Phys. Rev. 133 A111
[27] Vasilakis G 2011 Precision measurements of spin interactions with high density atomic vapors PhD dissertation Princeton Princeton university
[28] Allred J C Lyman R N Kornack T W Romalis M V 2002 Phys. Rev. Lett. 89 130801
[29] Happer W Tam A C 1977 Phys. Rev. 16 1877
[30] Ressler N W Sands R H Stark T E 1969 Phys. Rev. 184 102
[31] Gibbs H M Hull R J 1967 Phys. Rev. 153 132
[32] Lu J Qian Z Fang J 2015 Rev. Sci. Instrum. 86 043104
[33] Jiang L Quan W Liu F Fan W Xing L Duan L Liu W Fang J 2019 Phys. Rev. Appl. 12 024017
[34] Fang J Chen Y Zou S Liu X Hu Z Quan W Yuan H Ding M 2016 J. Phys. B: At. Mol. Opt. Phys. 49 065006
[35] Brown J M Smullin S J Kornack T W Romalis M V 2010 Phys. Rev. Lett. 105 151604
[36] Kornack T W Smullin S J Lee S K Romalis M V 2007 Appl. Phys. Lett. 90 223501
[37] Xing L Quan W Fan W Zhang W Fu Y Song T 2019 IEEE Access 7 63892