† Corresponding author. E-mail:
Project supported by the National Key Research and Development Program of China (Grant No. 2017YFB0701503).
The phase partition and site preference of Re atoms in a ternary Ni–Al–Re model alloy, including the electronic structure of different Re configurations, are investigated with first-principles calculations and atom probe tomography. The Re distribution of single, nearest neighbor (NN), next-nearest neighbor (NNN), and cluster configurations are respectively designed in the models with γ and γ′ phases. The results show that the Re atoms tend to entering γ′ phase and the Re atoms prefer to occupy the Al sites in γ′ phase. The Re cluster with a combination of NN and NNN Re–Re pair configuration is not preferred than the isolated Re atom in the Ni-based superalloys, and the configuration with isolated Re atom is more preferred in the system. Especially, the electronic states are analyzed and the energetic parameters are calculated. The electronic structure analyses show there exists strong Ni–Re electronic interaction and it is mainly contributed by the d–d hybridization. The characteristic features of the electronic states of the Re doping effects are also given. It is also found that Re atoms prefer the Al sites in γ′ side at the interface. The density of states at or near the Fermi level and the d–d hybridizations of NN Ni–Re are found to be important in the systems.
Ni-based superalloys are widely used as high-temperature materials in aircraft and land-based engine turbines due to their excellent material properties, such as thermal and mechanical properties.[1] The Ni-based superalloys comprises the face centered cubic (FCC) solid solution γ-Ni matrix phase and the L12-ordered γ′-Ni3Al phase. The high temperature strength of single crystal Ni-based superalloys can largely be attributed to γ and γ′ phase properties along with the properties of γ/γ′ interfaces.[2,3] Many alloying elements, such as Re, W, Ta, Ru, Mo, Cr, Co, Hf, are added into Ni-based superalloys to improve creep rupture life, strength, phase stability, oxygen resistance and so forth. Among the alloying elements, Re is a potent strengthener in Ni-based superalloys and plays an important role in improving the mechanical properties.[4,5] The so-called “rhenium-effect”, which was first discovered by Giamei and Anton,[6] means that the mechanical properties of Ni-based superalloys becomes better with a proper amount of Re addition. The effect of Re on improving mechanical properties can be explained from many aspects. It is found that Re can lower γ′ phase coarsening rate as well as resulting in a negative γ/γ′ misfit.[6,7] The synergistic effect of Re with other elements contributes to the strength of Ni-based superalloys.[8–10] Liu and Wang[11] studied the dislocation-doping complex in γ phase of Ni-based superalloys using lattice Green-function multiscale method. According to their study, the strengthening effect of Re can be attributed to the partitioning of Re in γ phase and its strong chemical interactions with dislocation.
In 1980 s, Blavette et al.[5] observed Re segregation to γ matrix and found Re-enriched region in the Ni-based superalloy using an atom probe field ion microscopy (FIM). Their results confirmed short range order of Re atoms in γ matrix phase. The observed Re clusters can act as obstacles for dislocation motion and can improve the creep strength. Wanderka and Glatzel[12] analyzed the second generation Ni-based superalloy CMSX-4 using atom probe field ion microscopy, and they found that Re atoms mainly form in γ phase and have a tendency to form clusters. They proposed that Re is likely to form cluster with roughly 5 atoms. Rüsing[13] studied the Re cluster using three-dimensional atom probe method and concluded that Re can form clusters with the size of approximately 1 nm. The molecular dynamics simulation and first-principles calculation results of Zhu et al.[14] showed that Re atoms tend to form clusters in both γ′ phase and γ phase, and the smallest Re cluster has a radius of 12.2 Å. Mottura et al.[15] found that Re–Re nearest neighbor pair has strong repulsion and Re atoms do not form clusters in γ phase by first-principles calculations. They also concluded that the so-called “rhenium-effect” cannot be the result of Re clustering and proposed that single Re atom is responsible for the strengthening effect. Lu et al.[16] calculated the binding energy of Re–Re pairs, and the study showed that the second nearest neighbor Re–Re pair in γ-Ni phase is more stable under 0 K. Ding et al.[17] studied the origin of Re effect on improving the mechanical properties of Ni-based superalloys. They demonstrated that the Re atoms tend to form Cottrell atmosphere at the interfacial dislocation core and stabilize the interfacial dislocation networks. The Re effect is the result of interaction between the local strain caused by Re and the strain caused by dislocations.
Until now, there is no commonly accepted view in whether the Re atoms form cluster or not in the Ni-based superalloys. What is more, the previous studies only considered the model of γ phase or γ′ phase in studying the Re distribution behaviors. The Ni-based superalloys contain two phases, and a model that can incorporate both γ and γ′ phases would be more realistic in studying the Re distribution. In this paper, we study different kinds of Re atom configurations across the γ/γ′ interface and analyze their energetics and electronic structures.
The γ′-Ni3Al separate out from the Ni-matrix and the usual precipitate directions are 〈001〉 directions. The interface structure and composition had been studied by several authors. The previous studies of Zhu and Wang et al.[14,18] indicate in general the γ/γ′ interface comprises a coherent interface region and a misfit dislocation region after sufficient relaxations. The interface width of Ni-based single crystal superalloys is found to be about 1 nm–3 nm from the experiment.[19–21] The order–disorder transition width is smaller than the chemical element transition width.[19] We adopt the coherent γ/γ′ interface in the calculations. The model adopted in this work is shown in Fig. 
For the purpose of studying the Re distribution in γ and γ′ phases, the different Re atom configurations are designed to occupy the sites of Ni and Al atoms in the systems (cf., Fig. 
For all the models in current research, ionic relaxation and self-consistent electronic structure relaxation are performed using the Vienna ab-initio simulation package (VASP) code,[22] which is based on density functional theory (DFT).[23,24] The ion–electron interaction is described by projector augmented wave (PAW),[25,26] and the generalized gradient approximation of Perdew–Burke–Ernzerhof (PBE)[27] exchange–correlation functional is used. The plane-wave cutoff energy is set to 350 eV. The convergence criterions for electronic and ionic step in the self-consistent calculations are 10−6 eV and 0.02 eV/Å, respectively. Spin-polarized calculations are not used. The integration over the Brillouin zone is performed using the 1 × 7 × 1 Monkhorst–Pack k-point mesh.[28]
Based on the ternary alloy designed by our group, the Ni–Al–Re model alloy is prepared to investigate the partitioning behavior of Re atom in γ and γ′ phases. The alloy is melted with the vacuum induction technique and is then directionally solidified to produce the 〈001〉-oriented single crystal. After the single crystal sample is prepared, it will perform the systematic heat treatment to obtain a near-equilibrium state alloy with γ and γ′ phases. The chemical analysis result of the ternary model alloy is Ni-7.95Al-4.94Re (wt%).
Atom probe tomography (APT) experiment is conducted to analyze the Re concentration in the model alloy. The APT specimen is wire-electrode cut from the heat-treated specimen into the dimension of 0.5 mm ×0.5 mm × 15 mm and is subjected to a standard two-step electro-polishing procedures.[29] The specimen temperature is ∼ 50 K. Proximity histogram (proxigram) methodology[30] is adopted to determine the concentration information.
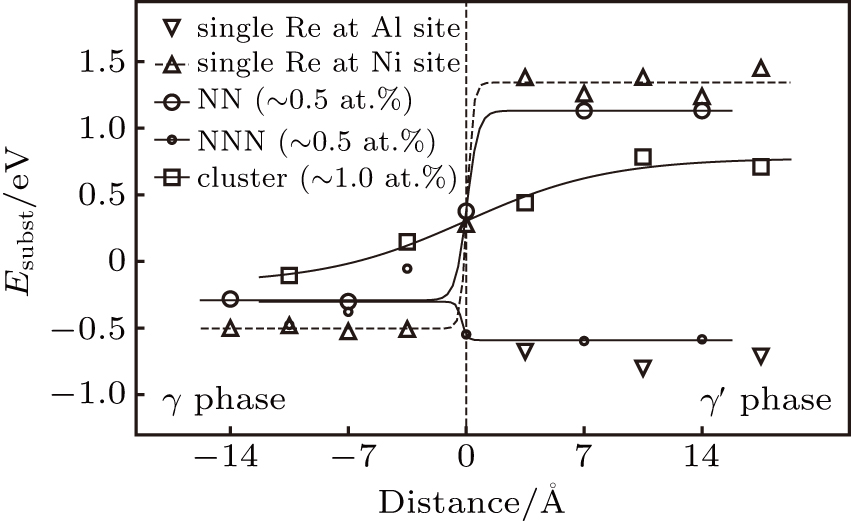
The substitution formation energy (Esubst) is defined as follows:[8]
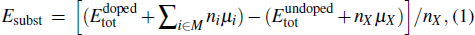

The calculated substitution formation energies are shown in Fig.
In γ′ phase, the systems with single Re atoms at Al sites (models S1, S3, and S5 in Fig.
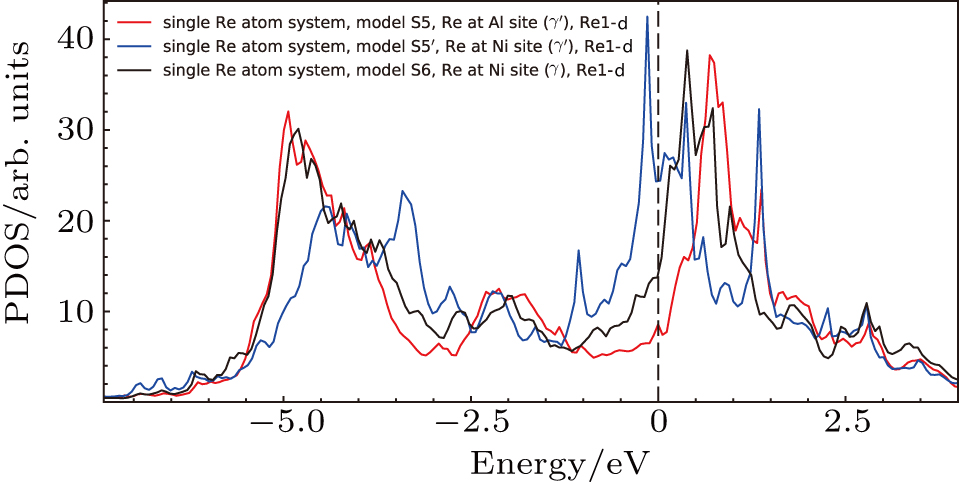
Comparing the Esubst of Re atoms at γ′/γ interface (model S5, S5′, S6), it can been seen that Esubst (model S5 single Re) < Esubst (model S6 single Re) < Esubst (model S5′ single Re). This indicates the fact that the Re atom at the interface prefer to occupy the Al site at γ′ side of the interface.
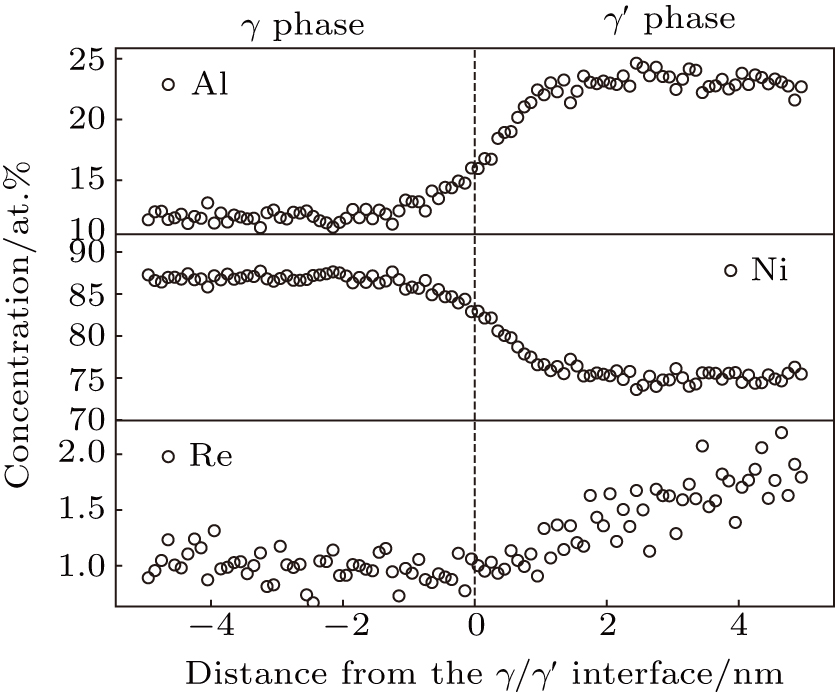
The concentration profile of Re in ternary alloy (Ni–Al–Re) is shown in Fig.
Thus, the simulation results of the Re atom occupying Al site is reasonable in our research. The calculated partition behavior and site preference of Re are consistent with the results of APT experiment.
To better understand electronic mechanism of Re atoms in the systems at microscopic level and the bonding characters of atoms, the interatomic energy,[33–35] the charge density difference (CDD), and the density of states (DOS) are studied. The electronic states and the interaction of atoms in the system can be expressed by the local density of states (LDOS) and the partial density of states (PDOS), which can give useful and detailed information of the underlying electronic mechanisms. The selected atoms in Fig.
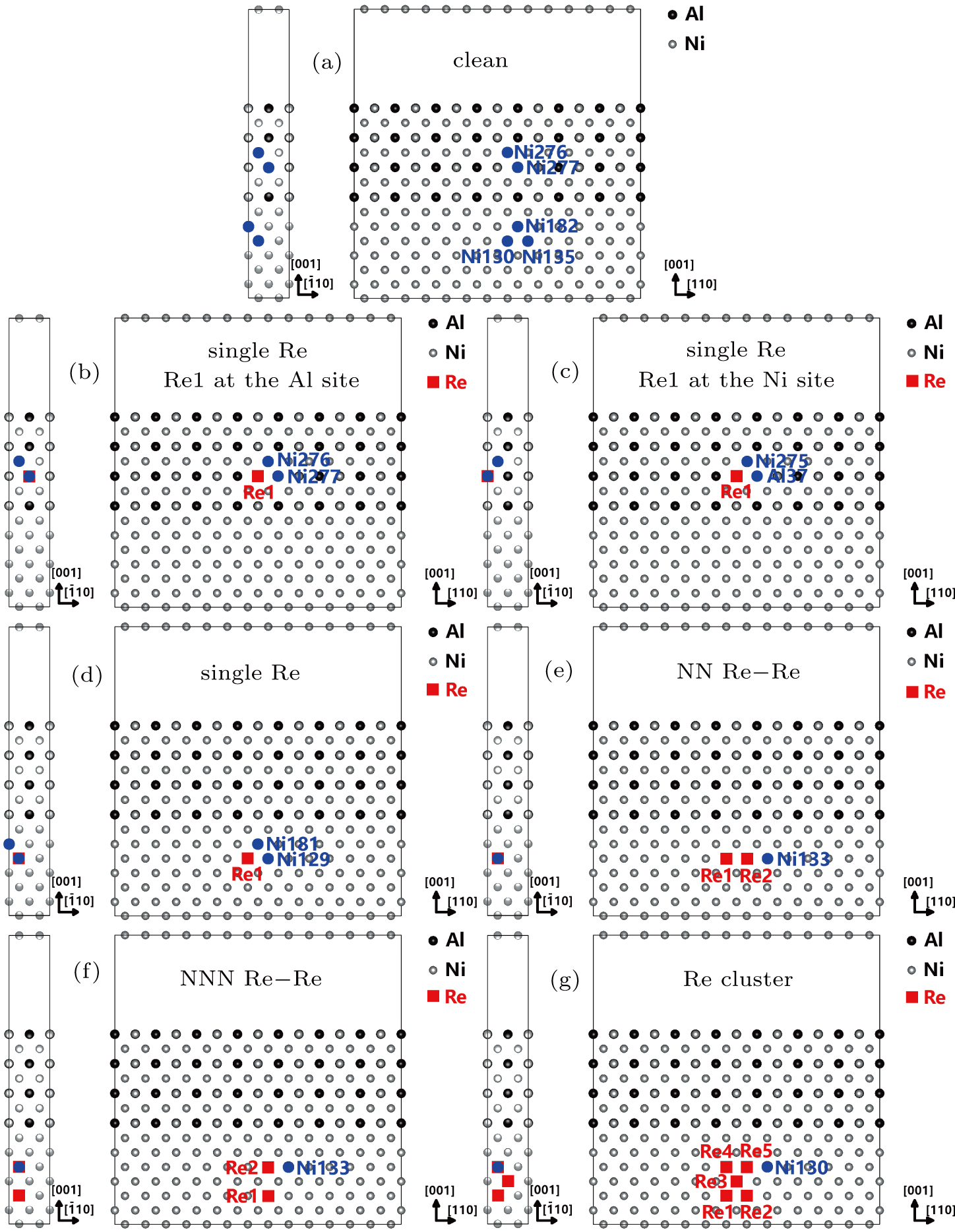 | Fig. 5. The Re atoms and their NN Ni atoms or NN Al atoms in the models with different Re atom distributions. |
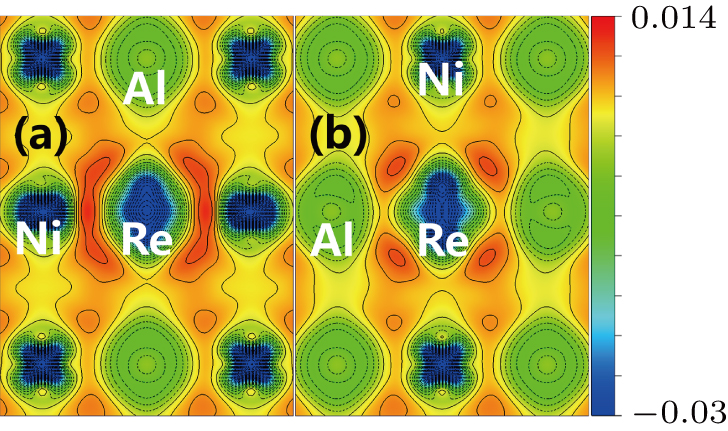
The site preference of the Re atom in γ′ phase can be explained from the charge density difference. It is seen from Fig.
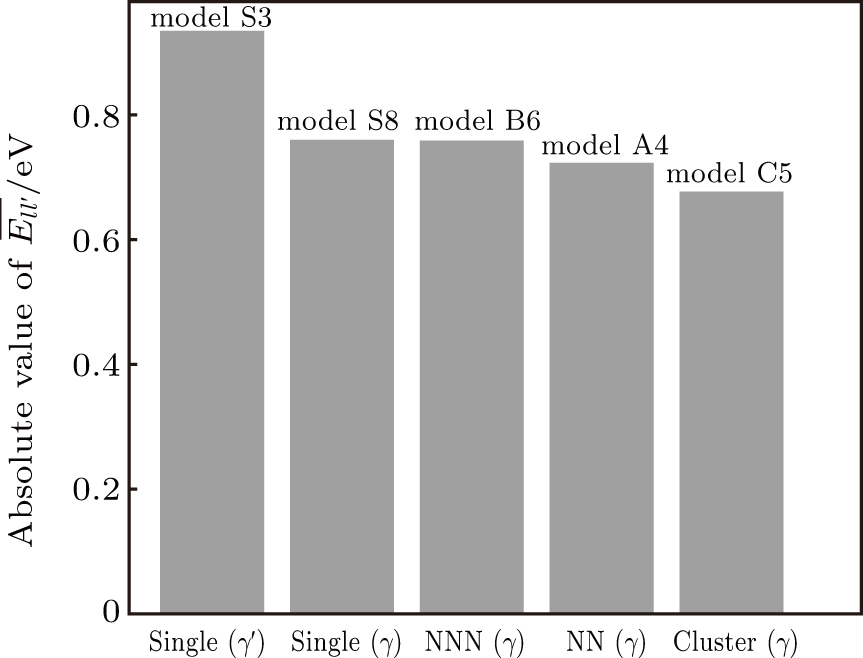
To explain the atom distribution of atoms in ternary model Ni-based superalloy, the charge accumulation and depletion are studied for the system with Re atom(s) in γ phase. The single Re atom, NN Re–Re, NNN Re–Re, and Re cluster systems are compared (models S8, A4, B6, and C5 in Fig.
The interatomic energy (IE) is a useful quantity which can characterize the bonding strength between atoms and interatomic interactions between atoms. The IE has been successfully used to study the electronic structure and properties of metals and alloys. The discrete variational method (DVM)[37,38] is used to compute the interatomic energy. The IE is derived as follows:[33–35]
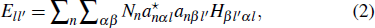
In Fig. 

The interatomic energies of NN Re–Re and NN Ni–Re for the systems in Fig. 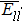
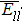
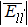
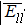

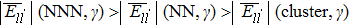
| Table 1. The interatomic energies (in units of eV) between atoms for different systems. . |
| Table 2. The averaged interatomic energies (in units of eV) of the doping elements for different systems. . |
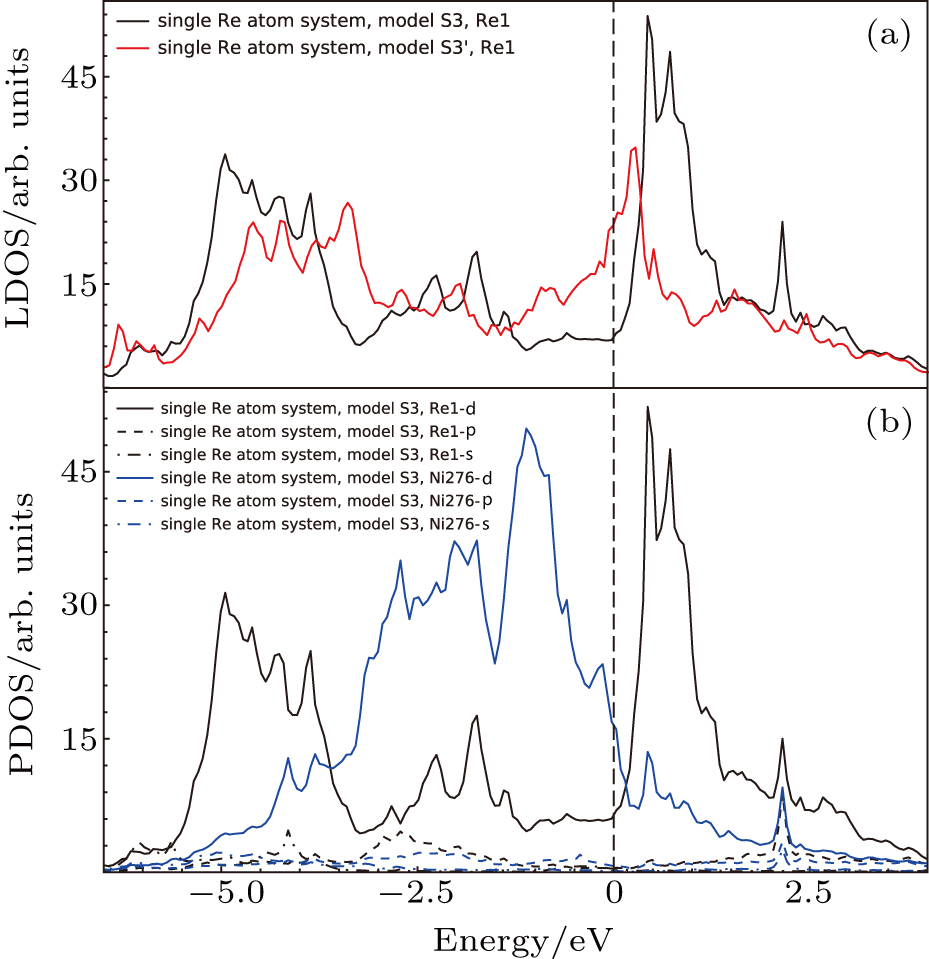
The LDOS’s of single Re atom occupying Al site (model S3 in Fig.
To analyze the contribution of each orbitals to the interaction between atoms, the PDOS’s of atoms in model S3 (cf., Fig.
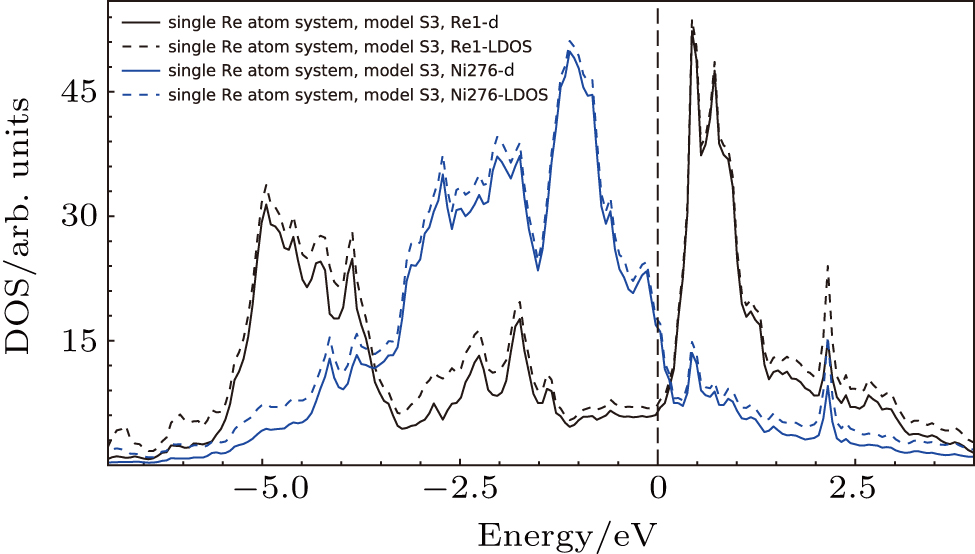 | Fig. 10. Density of states for the atoms in model S3 (cf., Fig. |
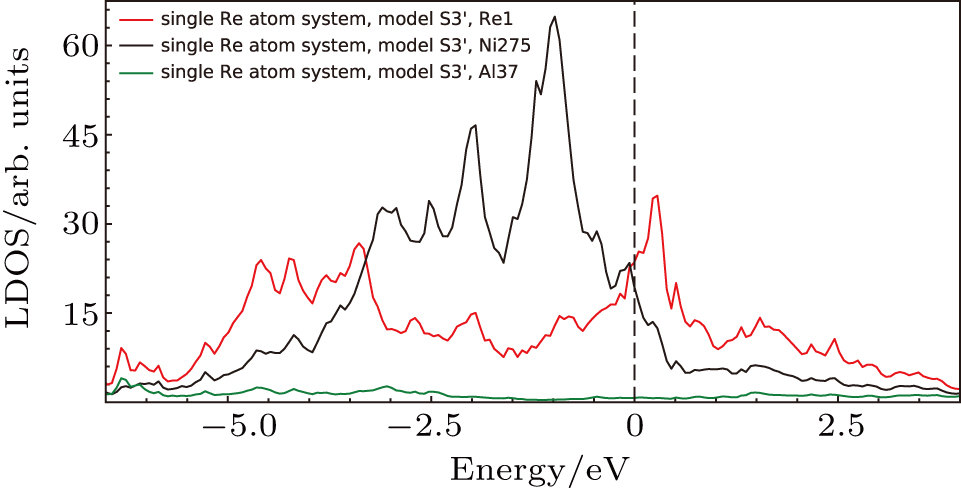
The LDOS’s of Re1, Ni275, Al37 in the system with single Re at Ni site in model S3′ (cf., Fig.
Based on the above features, it is found that the interaction of NN Ni–Re is stronger than NN Al–Re and the NN Ni–Re interaction is mainly contributed by the d–d hybridization. The density of states at or near the Fermi level and the NN Ni–Re d–d hybridization states play important roles in the system.
Three positions of Re atoms at interface are considered to analyze the interfacial electronic states. The first system is the system with Re atom at Al site in γ′ side near the interface (model S5 in Fig.
The electronic states of d orbitals for the S5, S5′, and S6 systems with Re atoms are shown in Fig.
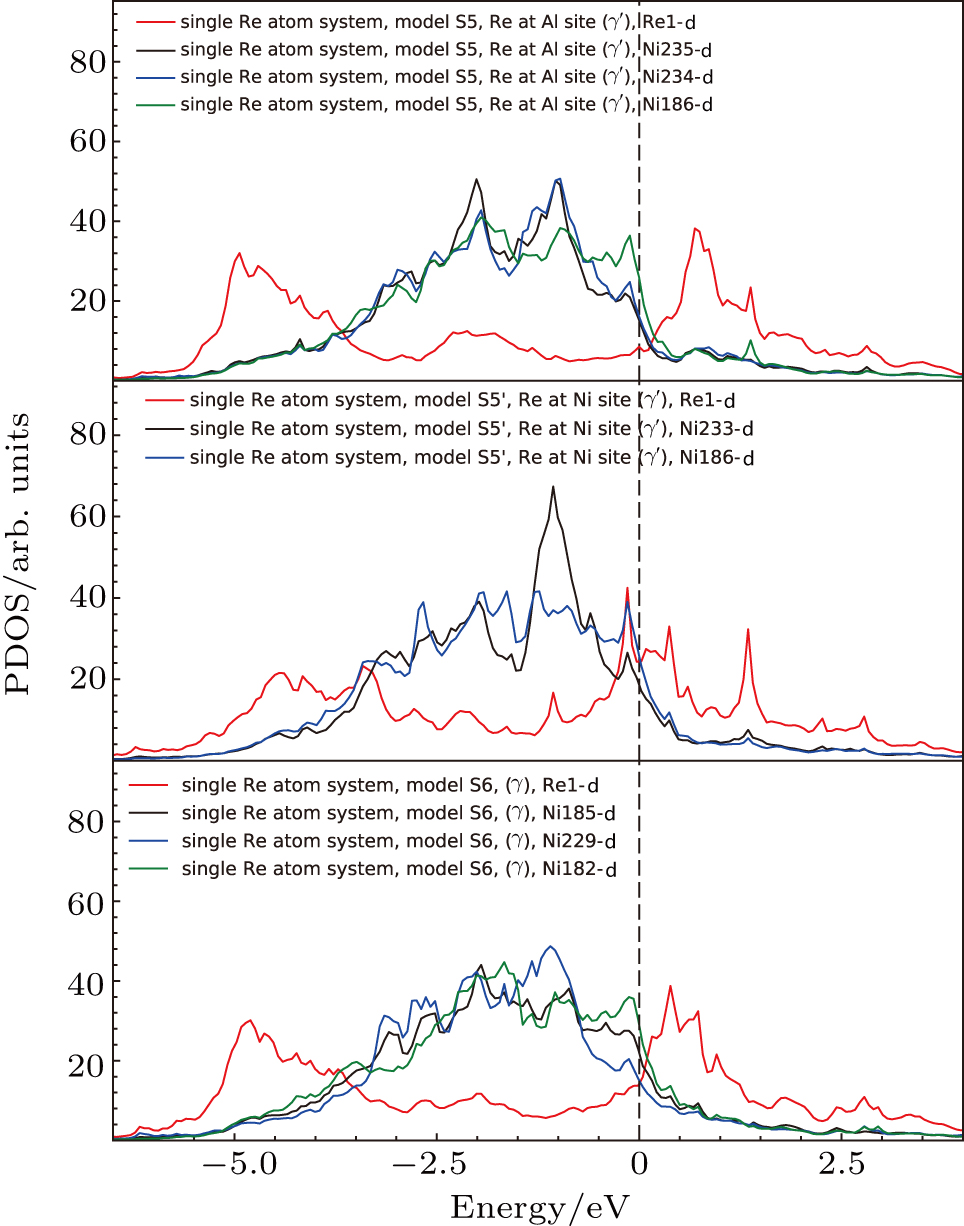
The d states of Re atoms and their inequivalent NN Ni atoms of the three systems are shown in Fig.
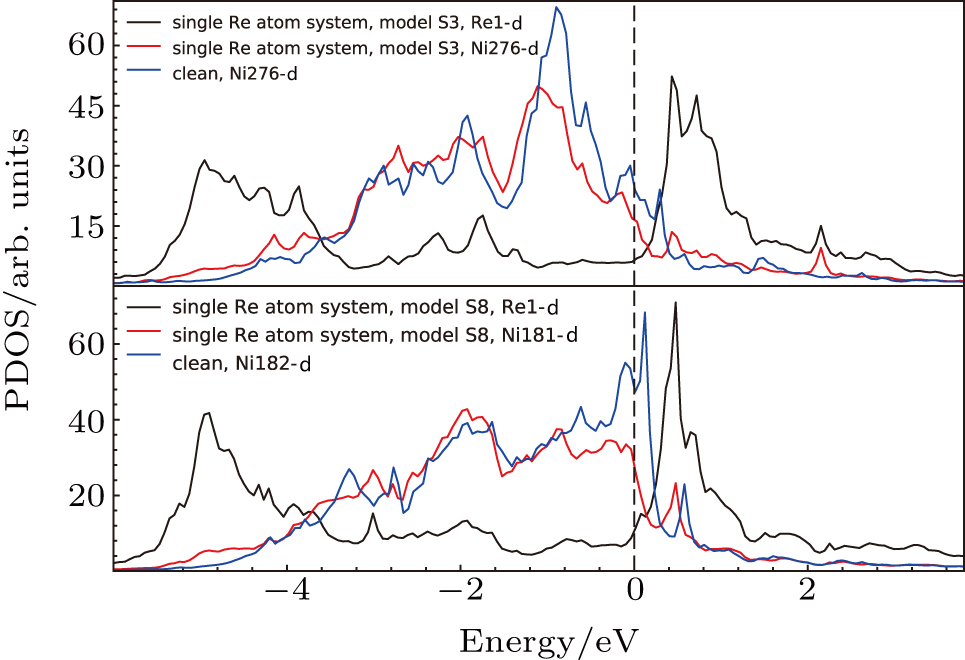
We investigated the effects of doping Re atoms on the system. From the above charge density analysis, the localized interaction feature of the doping atoms with their surrounding atoms can be seen. The above analysis on s, p, and d states showed the important contribution of d states of Re atom and Ni atom to the system. Thus, we focus on the effects of doping atoms on electronic states of their NN atoms and the PDOS of d states. The system without doping elements, the system with single Re atom at Al site in γ′ phase (model S3) and the system with single Re atom in γ phase (model S8) are compared and the PDOS are given in Fig.
The PDOS’s of Ni276 in model S3 and that of Ni276 in the system without Re are compared in Fig.
The d states of Ni and Re atoms in γ phase (model S8) have also been analyzed, and compared with those in the system without Re atoms (the system marked with “clean” in Fig.
The d states of the Ni atoms in γ phase after doping (the systems marked with “single Re”, “NN Re–Re”, “NNN Re–Re”, and “Re cluster”in Fig.
These results showed the effects of doping Re atoms on electronic structures of systems.
The first-principles method with the atom probe experiment is used to study the Re occupation behavior, Re distributions, and Re doping effects in the Ni-based superalloys. The Re partition behavior, site occupancy behavior, and favored existing configurations are systematically explored based on the model containing both γ and γ′ phases. The first-principles calculation results and the atom probe experiment results showed that Re atoms prefer γ′ phase and occupy Al sites in Ni–Al–Re ternary alloy. The isolated Re atoms are energetically preferred in γ′ phase of ternary Ni–Al–Re alloy. The electronic states and the electronic structures are analyzed. The results of electronic structure analyses showed that there exist strong NN Ni–Re interactions and the strong interaction of Ni–Re is mainly contributed by the d–d electron interactions. The formation of d–d hybridizations between NN Ni atoms and Re atoms after doping Re atoms is observed and validated. The density of states at or near the Fermi level and the d–d hybridizations of NN Ni–Re are found to be important in the systems. The energetics and the electronic structure analyses also showed that near the interface, the Re atom prefers Al site in γ′ side and it can be seen to be natural.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] |