† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11634010, 91850118, 11774289, 61675168, and 11804277), the National Key Research and Development Program of China (Grant No. 2017YFA0303800), the Joint Fund of the National Natural Science Foundation of China and the China Academy of Engineering Physics (Grant No. U1630125), and the Fundamental Research Funds for the Central Universities, China (Grant Nos. 3102018zy036, 3102019JC008, and 310201911cx022).
Recently, physical fields with topological configurations are evoking increasing attention due to their fascinating structures both in fundamental researches and practical applications. Therein, topological light fields, because of their unique opportunity of combining experimental and analytical studies, are attracting more interest. Here, based on the Pancharatnam–Berry (PB) phase, we report the creation of Hopf linked and Trefoil knotted optical vortices by using phase-only encoded liquid crystal (LC) holographic plates. Utilizing scanning measurement and the digital holographic interference method, we accurately locate the vortex singularities and map these topological nodal lines in three-dimensions. Compared with the common methods realized by the spatial light modulator (SLM), the phase-only LC plate is more efficient. Meanwhile, the smaller pixel size of the LC element reduces the imperfection induced by optical misalignment and pixellation. Moreover, we analyze the influence of the incident beam size on the topological configuration.
With the development of laser technology in various realms, exploring light fields with ingenious spatial structures and intriguing evolution features is becoming a hot spot of optics and photonics. In recent years, optical vortices carrying orbital angular momenta (OAM) and two-dimensional phase singularities have drawn extensive attention and been exploited in various applications, including optical imaging,[1,2] particles manipulation,[3,4] optical information storage,[5] communication,[6,7] and so on.[8–10] Recently, a special kind of optical fields, whose vortex singularities are three-dimensionally connected as isolated loops in the forms of topological configurations such as vortex knots and links,[11–15] has aroused great concerns.
Since the theoretical proposal of Lord Kelvin,[16] the knots and links have been demonstrated playing a fundamental role in a wide range of physical branches such as plasmas,[16,17] quantum field,[18] classical fluid,[19,20] and liquid crystals.[21,22] In optical regime, the model in which the vortex lines (connected vortex singularities) can be knotted or linked and show topological structures was first theoretically reported by Berry and Dennis in 2001,[23] and experimentally constructed by Leach et al. based on the linear superposition of Laguerre–Gaussian (LG) beams with optimized intensities and phases.[24,25] Such vortex lines in light fields can be potentially applied as a topological waveguide for quantum mechanical matter waves, such as Bose–Einstein condensates.[26,27] Furthermore, because the light fields exhibit an unique opportunity of combining experimental and analytical studies, the optical topology is attracting more attention for studying topological fields and furthermore understanding the common topological configurations in disparate matter systems. To precisely create topological vortices, the holographic reconstruction based on a spatial light modulator (SLM) is a common approach. However, for this method, the disadvantages induced by the relatively large pixel size of the SLM, such as misalignment and pixellation, limit the construction perfection. Therefore, an efficient optical device with smaller pixel is necessary to overcome such issues.
In this paper, we report the creation of topological vortices by using liquid crystal (LC)[28] holographic Pancharatnam–Berry (PB) phase[29,30] plates fabricated via sulphonic azo-dye SD1 based photoalignment technology and digital micro-mirror device (DMD) based dynamic exposure process. The continuous orientation of the LC molecules in such a PB phase plate reduces the imperfection arising from pixelated SLM, allowing the precise reconstruction of three-dimensional (3D) vortex singularities, namely, topological vortices. Moreover, we adopt the scanning measurement and the digital holographic interference methods to accurately map the topological configurations, locating the vortex singularities in 3D space. These designed LC plates with high performance provide a way to extend further fundamental study and applications of topological vortices.
To design and fabricate LC plates, we start from the configuration of isolated topological structures. The common realization method is the linear superposition of LG fields with optimized coefficients and beam widths according to the Milnor polynomials.[25] Theoretically, considering the 3D topological field as a solution of the Helmholtz equation, we decompose the topological fields at the z = 0 plane into multiple LG fields, i.e., 


In order to simultaneously control the amplitude and phase of the light fields shown in Eq. (
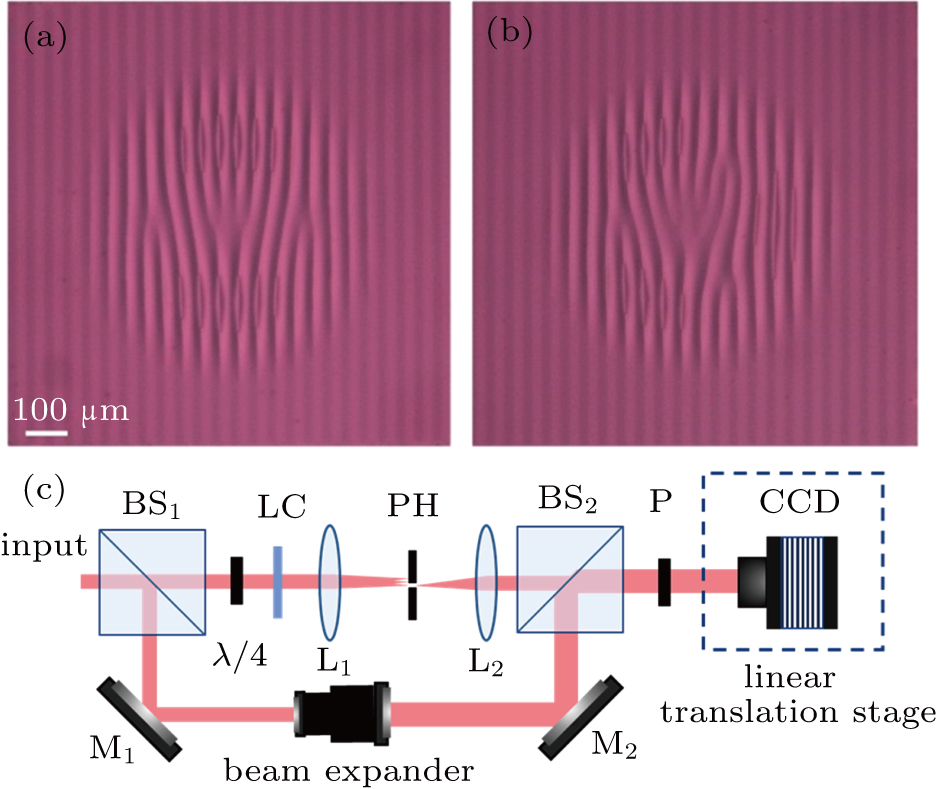
Next, we map the holograms into LC plates by using sulphonic azo-dye SD1 based photoalignment technology and DMD based microlithography system[32,33] with a spatial resolution of 1.08 μm×1.08 μm. Via an eighteen-step five-time-partly-overlapping exposure process,[34,35] a director variant LC PB phase plate can thus be formed. The corresponding polarized optical microscopic images are shown in Figs.
The experimental setup to observe the topological vortices generated from the LC plates is shown in Fig.
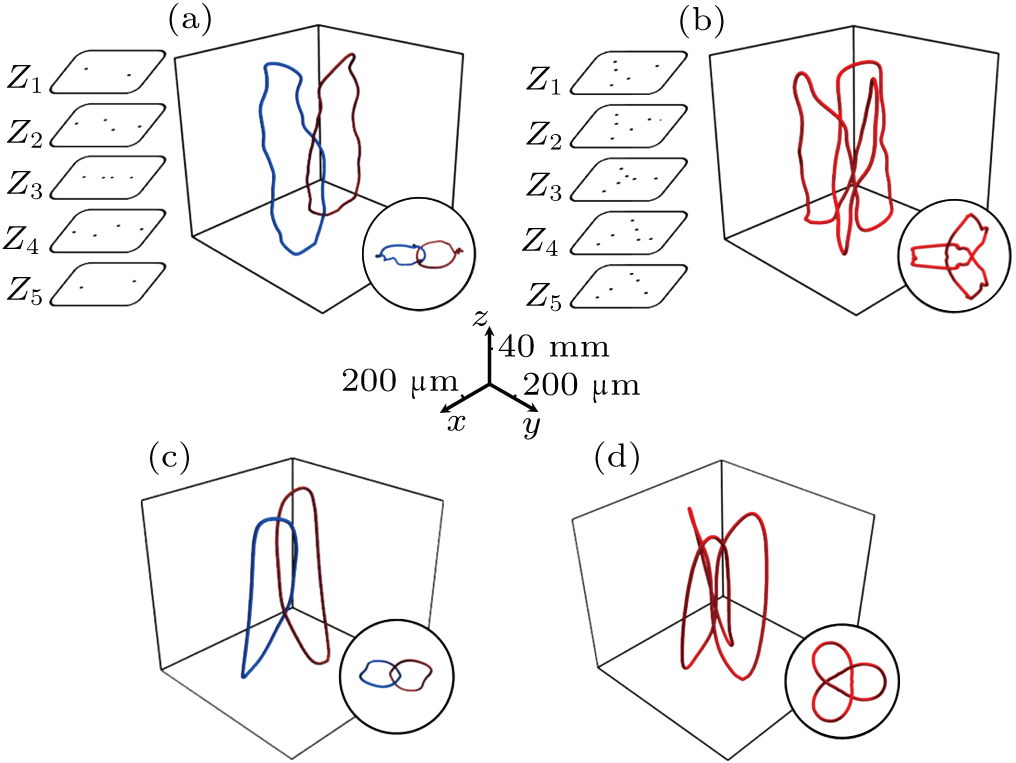
Figure
Further, we measure the distribution of phase singularities in 3D space by scanning different planes along the z direction.[40] The left charts of Figs.
The above experimental results demonstrate the successful generation of topological vortices by using PB phase LC plates. Compared with the configurations constructed from SLM, here reported ones have smaller geometry and therefore enable the more perfect construction of the vortex links and knots. Actually, the geometric size of the topological configurations is directly dependent on the scale of the hologram. Here, the size advantage of the LC molecules enables the more perfect construction. Besides, it is noteworthy that, the incident beam waist can also affect the topological configurations. Therefore, we further explore the influence of the size of the incident beam on the constructed configuration. Figure
Figure
We constructed two typical topological vortices of Hopf link and Trefoil knot via phase-only LC holographic plates, and accurately mapped the topological configurations by experimentally measuring the complex amplitude and phase distributions of 3D fields. Compared with the traditional methods using SLM, the PB phase LC plate has great advantages in size and cost, which ensures the generation quality and diversity. Moreover, the PB phase LC plate can operate in a wide spectrum range. This work supplies a versatile candidate for creating high quality topological vortices and may pave a way to extend further fundamental study and applications of topological vortices.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] |