† Corresponding author. E-mail:
Project supported by the National Key Technology Research and Development Program of the Ministry of Science and Technology of China (Grant No. 2017YFC083300), the National Natural Science Foundation of China (Grant Nos. 91646201, U1633203, and 51808422), and the Independent Innovation Foundation of Wuhan University and Technology, China (Grant No. 2019IVA011).
Pedestrian evacuation is actually a process of behavioral evolution. Interaction behaviors between pedestrians affect not only the evolution of their cooperation strategy, but also their evacuation paths-scheduling and dynamics features. The existence of interaction behaviors and cooperation evolution is therefore critical for pedestrian evacuation. To address this issue, an extended cellular automaton (CA) evacuation model considering the effects of interaction behaviors and cooperation evolution is proposed here. The influence mechanism of the environment factor and interaction behaviors between neighbors on the decision- making of one pedestrian to path scheduling is focused. Average payoffs interacting with neighbors are used to represent the competitive ability of one pedestrian, aiming to solve the conflicts when more than one pedestrian competes for the same position based on a new method. Influences of interaction behaviors, the panic degree and the conflict cost on the evacuation dynamics and cooperation evolution of pedestrians are discussed. Simulation results of the room evacuation show that the interaction behaviors between pedestrians to a certain extent are beneficial to the evacuation efficiency and the formation of cooperation behaviors as well. The increase of conflict cost prolongs the evacuation time. Panic emotions of pedestrians are bad for cooperation behaviors of the crowd and have complex effects on evacuation time. A new self-organization effect is also presented.
Pedestrian flow dynamics and human behaviors in emergency are important topics for the prevention and control of disasters. They have been attracting great attention from various circles of researchers for several decades. In a pedestrian-particle system in emergency, plenty of agents crowd together and interact with each other, which may bring various self-organization phenomena such as arching, herding behaviors, “faster-is-slower” effect,[1] etc.
Many physical models have reproduced those phenomena, which are conducive to understanding the mechanism of the phenomena and analyzing the properties of the crowd dynamics. In general, pedestrian evacuation models can be classified as microscopic models and macroscopic models. The macroscopic models are based on the network with modeling the pedestrians as fluid flow, with the shortage of the depiction about the heterogeneity and subjective interaction among pedestrians. In contract, microscopic models simulate agents as individuals, which can address the problems commendably. Social force model[2–4] and cellular automata models including floor field models,[5,6] lattice gas models,[7,8] multi-grid models,[9,10] agent-based models,[11] potential field models,[12] etc. are two kinds of representative microscopic models. The social force model is a multi-particle self-driven model based on newtonian mechanics, which is not very suitable for complex and large-scale movements of pedestrians due to the computational efficiency, while cellular automata models divide the walking space into grids and employ the time-step for evolution, thereby improving the computational efficiency greatly.
In an evacuation process, the movements of individuals and the crowd are all affected by environmental factors[13–16] and human factors.[17–21] To escape from the dangerous areas as fast as possible, pedestrians may schedule their paths in real time and change their behaviors constantly given by these factors. That is to say, the process of pedestrian evacuation is also a process of behavioral evolution. It is noted that as a social system of pedestrians, there exits a huge and complex network due to relationships and interdependence among pedestrians.[22,23] Pedestrians learn from and interact with each other, especially with their neighbors. Interaction behaviors between pedestrians affect not only the evolution of their cooperation behaviors, but also their decision makings to path scheduling based on the facts that people intend to choose better neighbors and gain more benefits, which can have better advantages to arrive at the safe area. Game theory has been introduced into the evacuation models to investigate pedestrian dynamics and cooperation evolution, in which payoff matrix is used to calculate the interactions payoffs between pedestrians. Zheng et al.[24,25] firstly integrated the game-theoretical method with static floor field evacuation model to study individual cooperative behaviors, and the interaction payoffs only between pedestrians who strive for the same position are focused. Zhang et al.[26] further considered the compassion mechanism in the conflicts when more than one pedestrian tries to occupy the same position in the model, and its effects on evacuation dynamics and cooperation evolution are studied. Unlike previous study, Shi et al.[27] and Guan et al.[28] used the game theory model to deal with the interaction between neighboring pedestrians. Average interaction payoffs were proposed as inputs to calculate the probability of one pedestrian to enter into the targeted position and update his strategy according to different rules. However, the latter studies[28] lost the sight of the effects of interaction between neighbors on the decision making how to move for one pedestrian, and as most previous study did, the former study[27] addressed this but did not discussed comprehensive influences of interaction behaviors nor environment factors on pedestrian movement, and conflicts among pedestrians who compete for the same position were also neglected. Even though the existing researches have concerned themselves with the effects of interaction behaviors between pedestrians on pedestrian movements, how interaction behaviors and environment factors synthetically affect decision-makings of one pedestrian to path scheduling is still limited. Further study is necessary to reveal the influences of interaction behaviors as well as other subjective factors on cooperation evolution and movement dynamics of pedestrians in such a situation.
In this paper, we extend the cellular automaton model to the investgating of the evolutional strategy and the individual movement based on the game theory. In this model, the influence mechanism of the environment factor and interaction behaviors between neighbors synthetically on the decision-making of one pedestrian to path scheduling is focused on. The parallel update scheme is investigated and a new method to solve the conflicts when more than one pedestrian competes for the same position is proposed. The reminder of this article is structured as follows. In Section
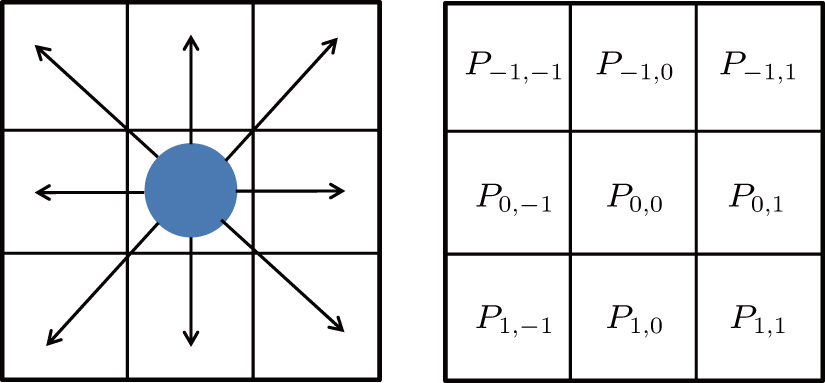
Our model is defined on a squared domain divided into a number of discrete grids. Each grid can be either empty or occupied by sole one pedestrian. In our work, the size of a grid is set to be 0.4 m × 0.4 m, and an pedestrian can move to an empty grid or stay still at each step, here we take a simulation step length to be 0.3 s. Pedestrians make decisions consistently when scheduling their path from one grid to next one grid. To incorporate effects of interaction behaviors and environment factors into the decision-making process of one pedestrian, an extended model given by the exponential is proposed, namely, the transition probability Pij of one pedestrian to a target cell can be formulated as follows:
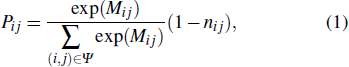

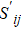
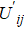
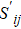


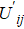
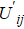


| Table 1. Payoff matric of snowdrift game. . |
The parallel update scheme is utilized in this paper. One significant problem is to solve the conflicts when more than one pedestrian competes for the same position. The average payoffs of one pedestrian interacting between his neighbors are introduced to reflect his competitive ability. Therefore the target cell is occupied by the pedestrian whose position is (i, j) with the following probability
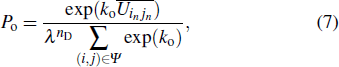

We also suppose that the pedestrians are rational. Pedestrians who cannot move during the conflicts will adjust their strategy with the probability according to Eq. (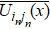
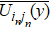

The simulation procedure for the evacuation process is elaborated as follows:
Initialize the positions and strategies of pedestrians. All pedestrians are distributed randomly in the domain with the density of ρ = N/M, where N and M are the number of pedestrians and grids in domain respectively, and the initial fraction of cooperators is set to be ρco. Compute the transition probability for each pedestrian according to Eq. ( Update the position of pedestrians with the parallel method. If there is more than one pedestrian striving for the same cell, conflicts are solved with Eq. ( Update strategies for pedestrians. The pedestrians involved in the conflicts and not moving at the step will update their strategies according to Eq. ( Repeat Steps 2, 3, and 4 for each pedestrian. The pedestrian arriving at the exit will be removed from the system.
To provide trustworthy results, each test is simulated 50 times and the mean values are exhibited. The strategy of the pedestrian in the last step is recorded as the calculation of the final ρc.
The simulations are carried out in a room with the size of 10 m× 10 m. Only one door occupying one grid exists on the sites, it is located in the center of the bottom wall. Initially, all pedestrians are distributed uniformly with the density ρ = 0.6 and ρco = 0.5. We also set ko = kc = 2 in this paper. Figure
Figure
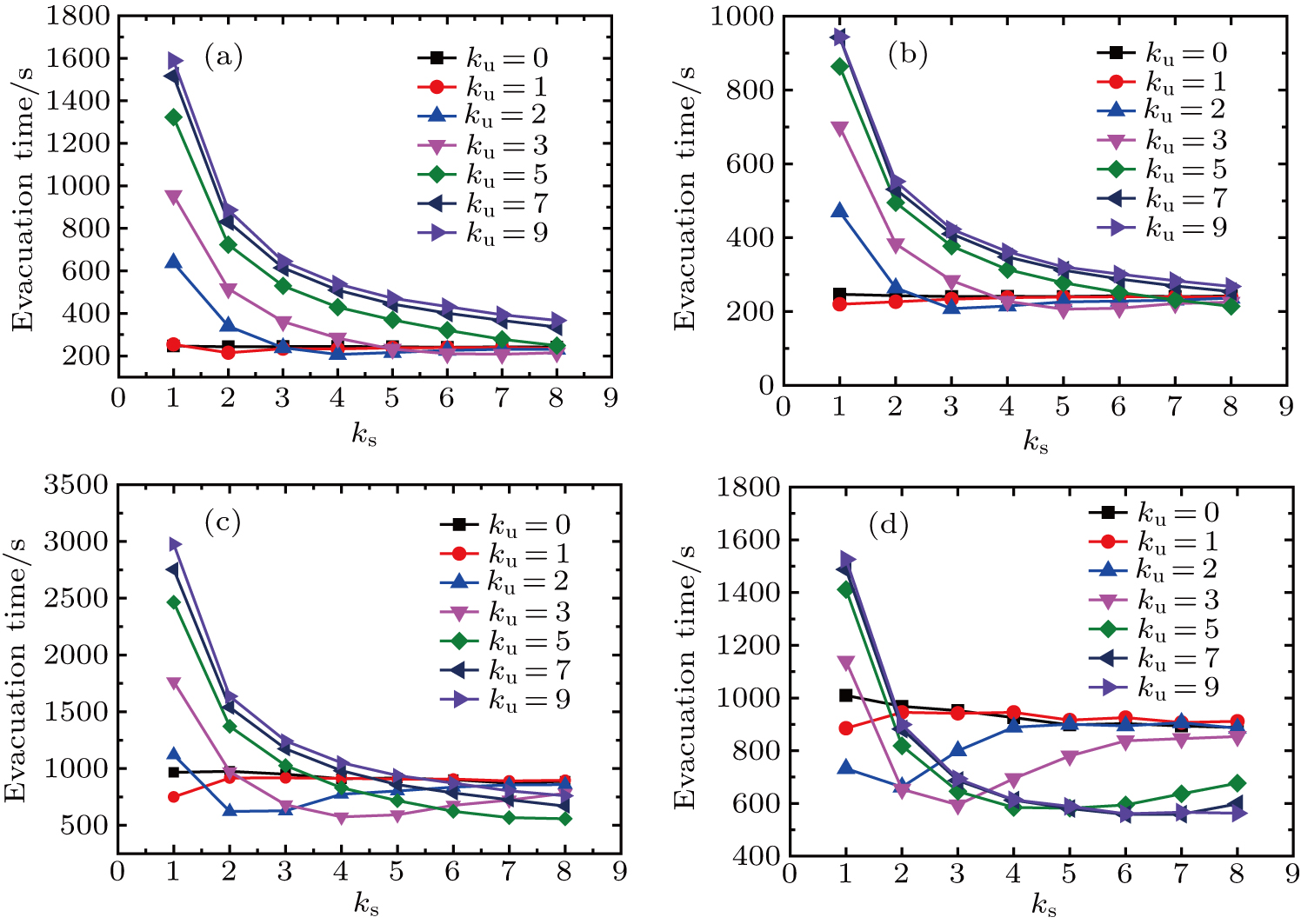 | Fig. 3. Evacuation times with different values of ks and ku: (a) r = 0.3, λ = 1.2; (b) r = 0.7, λ = 1.2; (c) r = 0.3, λ = 1.6; (d) r = 0.7, λ = 1.6. |
Figure
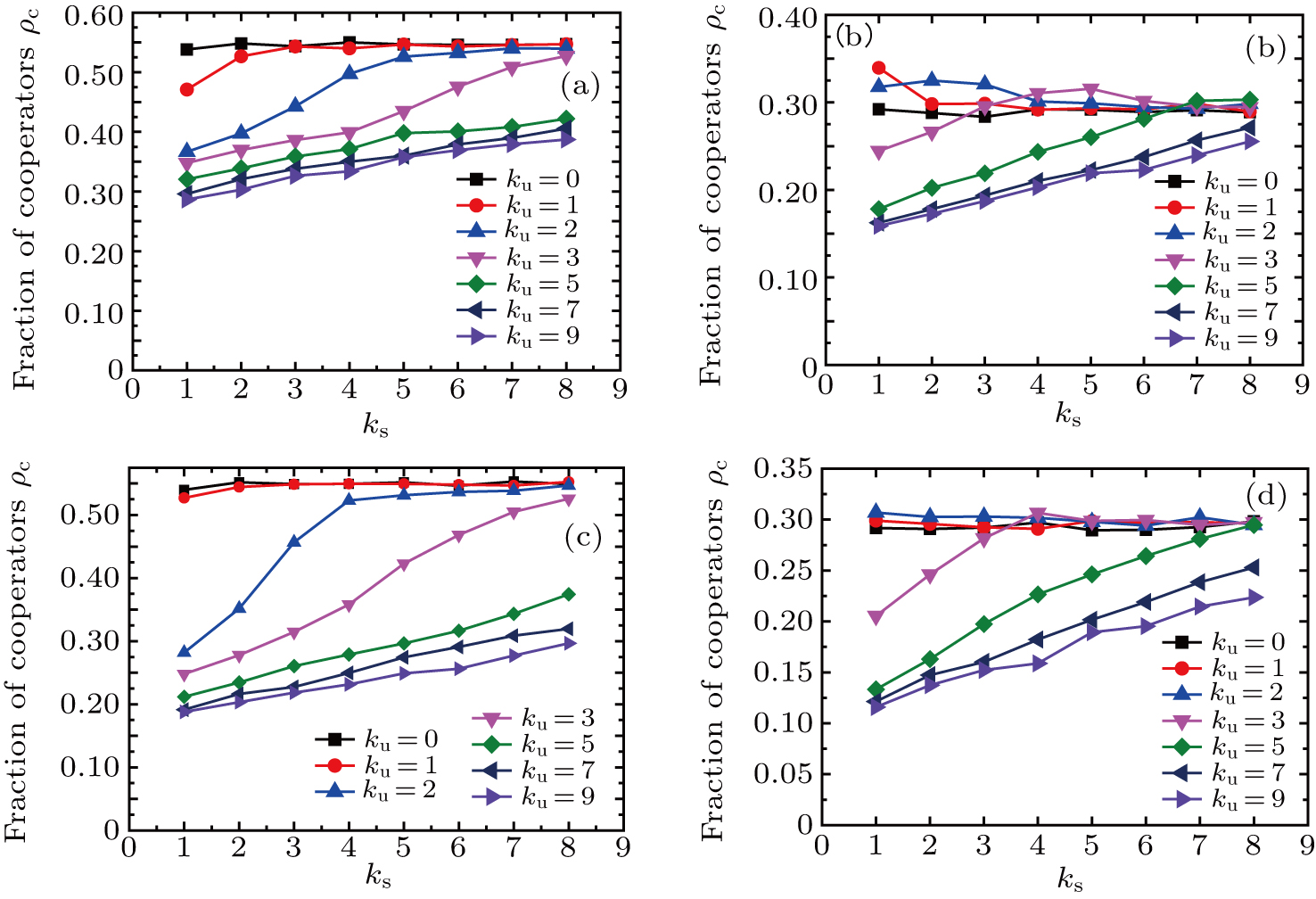 | Fig. 4. Fractions of cooperators with different values of ks and ku: (a) r = 0.3, λ = 1.2; (b) r = 0.7, λ = 1.2; (c) r = 0.3, λ = 1.6; (d) r = 0.7, λ = 1.6. |
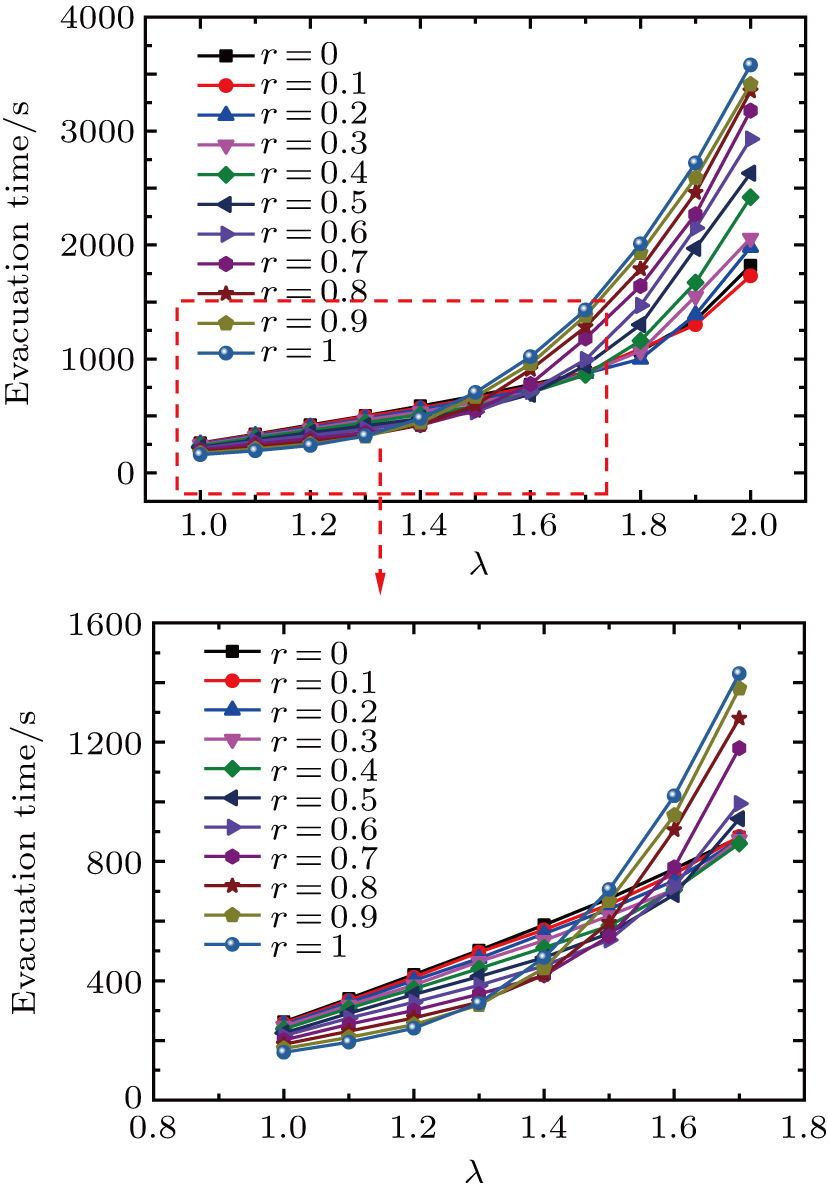
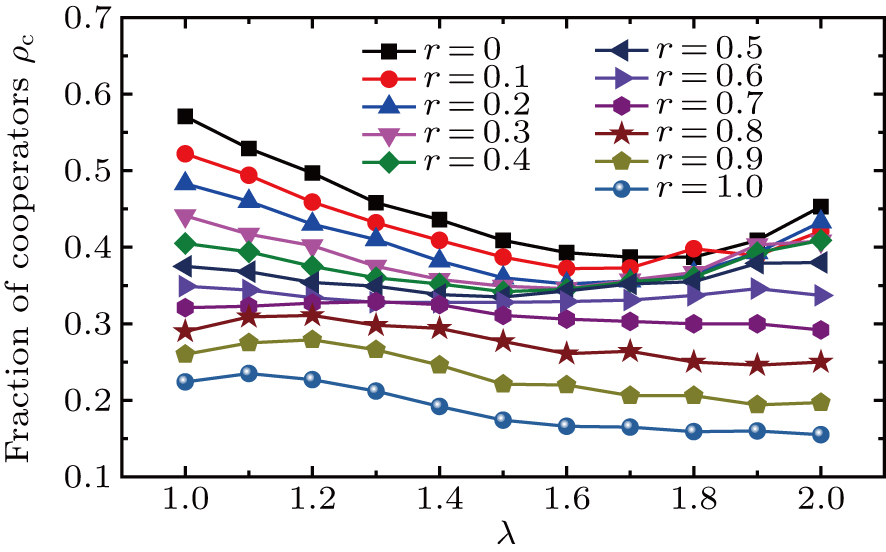
The panic degree r and conflict cost λ have an influence on the evacuation process of pedestrians, as illustrated in Figs.
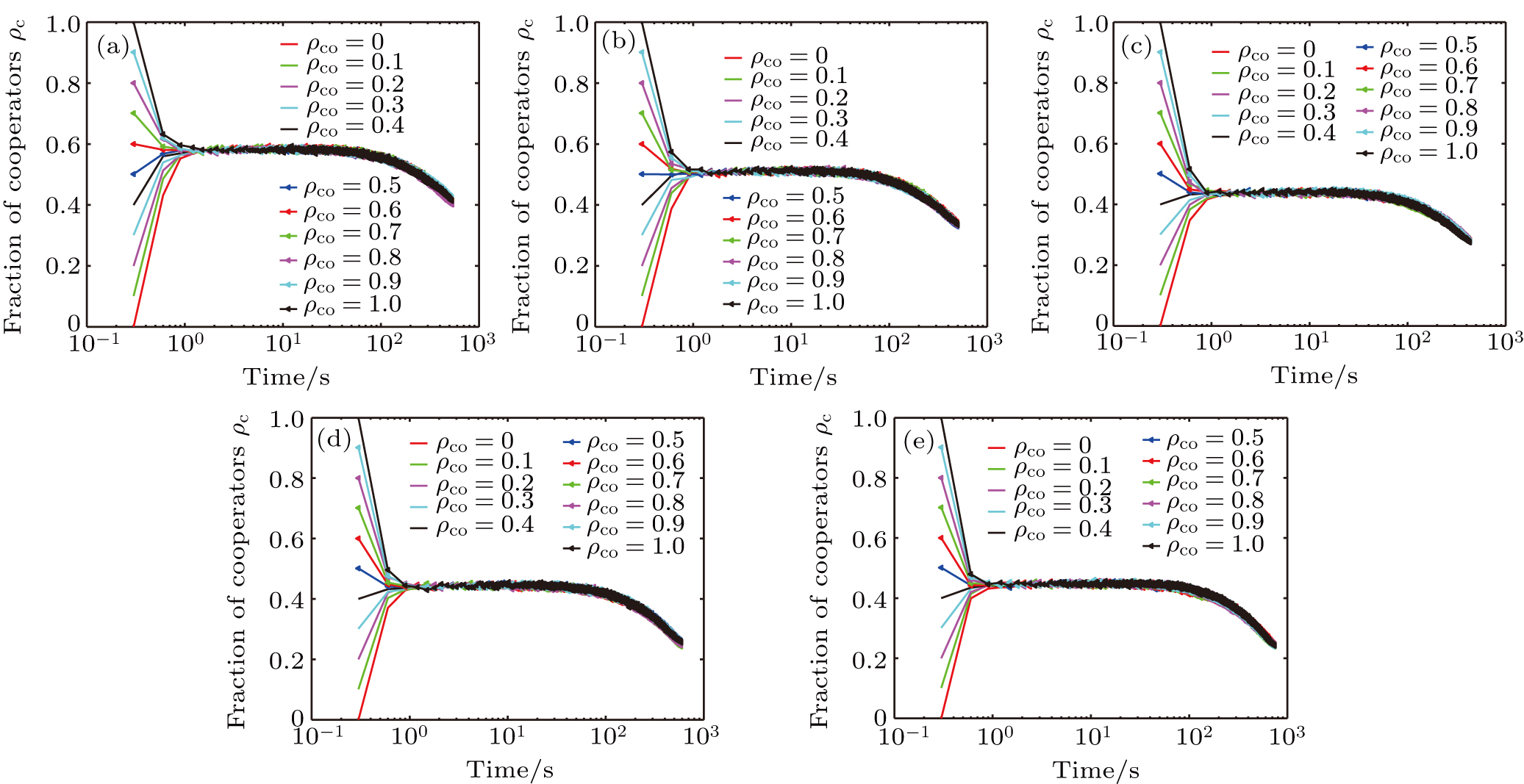
The tendency of varying with λ depends on the value of r. The fraction of cooperators first decreases and then increases slightly when r < 0.7, otherwise goes up imperceptibly and falls down directly when r ≥ 0.7. This can be explained as the fact that larger value of λ makes smaller the possibility for pedestrians to move, pedestrians prefer to become defectors to obtain more payoffs from neighbors and more chances to move, but neighboring defectors compete for less payoffs and more defectors further reduce the possibility to move as shown in Eq. (
The pedestrians’s evacuation time also varies with r under different values of λ. When λ is relatively small, large values of r lead evacuation time to lessen otherwise the contrary results are obtained as shown in Fig.
The fraction of cooperators decreases with the increase of r value, which obviously indicates that panic emotions of pedestrians are bad for their cooperative behaviors. This is because the bigger the value of r, the more the payoffs they obtain as a defector from a cooperator according to the snowdrift game theory, and therefore they are more likely to move as shown in Eq. (
 | Fig. 7. Evolution processes of cooperator fraction with time at different values of r for (a) λ = 1, (b) 1.2, (c) 1.4, and (d) 1.6. |
In what follows, the evacuation dynamics and cooperation behaviors with different values of ρco are investigated as shown in Fig.
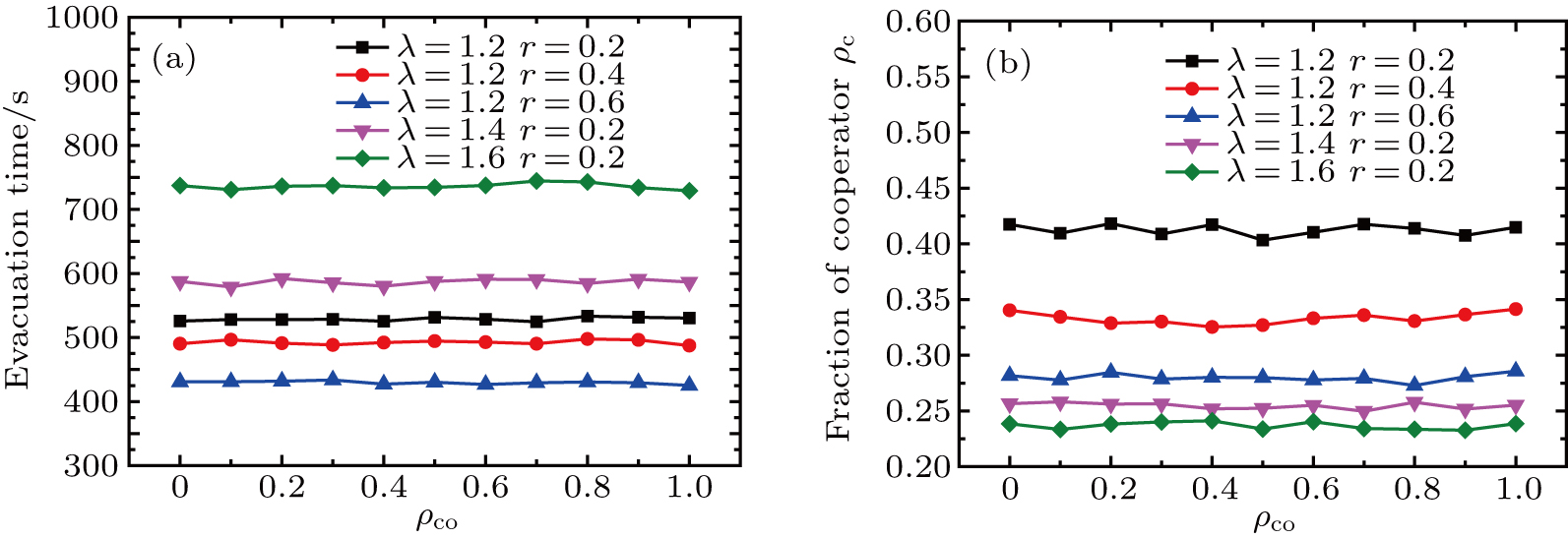 | Fig. 8. Plots of evacuation time and fraction of cooperators versus ρco for different values of λ and r. |
In this paper, an extended evacuation model considering the effect of interaction behaviors between neighboring pedestrians and the evolution of cooperation behavior is proposed based on the CA model and the game theory model. In the model, one pedestrian’ decision-making to path scheduling is determined together by benefits from interaction behaviors and static environment. The parallel update scheme is adopted and a new method based on the average payoffs of one pedestrian interacting with his neighbors is presented to reflect his competitive ability. Fermi rule is used to update the cooperative or defective strategy of pedestrians. According to the model, the influences of interaction behaviors, panic index and conflict cost on the evacuation time and the cooperation evolution of pedestrians are further analyzed. The results indicate that interaction behaviors between neighboring pedestrians can reduce the evacuation time to a certain extent. When the interdependence degree is small, it is conducive to the formation of cooperation behaviors. Large conflict cost of defectors lengthens the evacuation time. Panic emotions of pedestrians are bad for their cooperative behaviors. When λ is relatively small, large values of r lead the evacuation time to lessen, otherwise the contrary results are obtained. In addition, a kind of self-organization effect is present in the evolution process of cooperation behavior, that is, the fraction of cooperators reaches a consistent state rapidly in spite of different values of parameters. This work offers a new insight into the understanding of the dynamic mechanism of pedestrian evacuation and also provides guidance for establishing the evacuation strategies.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] |