† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11674375, 11634015, 11925408, and 11674369), the National Basic Research Program of China (Grant Nos. 2016YFA0300600, 2016YFA030240, 2017YFA0302901, and 2018YFA0305700), the Strategic Priority Research Program and Key Research Program of Frontier Sciences of the Chinese Academy of Sciences (Grant Nos. QYZDB-SSW-SLH013, XDB28000000, and XXH13506-202), the Science Challenge Project of China (Grant No. TZ2016004), the K. C. Wong Education Foundation, China (Grant No. GJTD-2018-01), the Beijing Natural Science Foundation, China (Grant No. Z180008), and the Beijing Municipal Science and Technology Commission, China (Grant No. Z181100004218001).
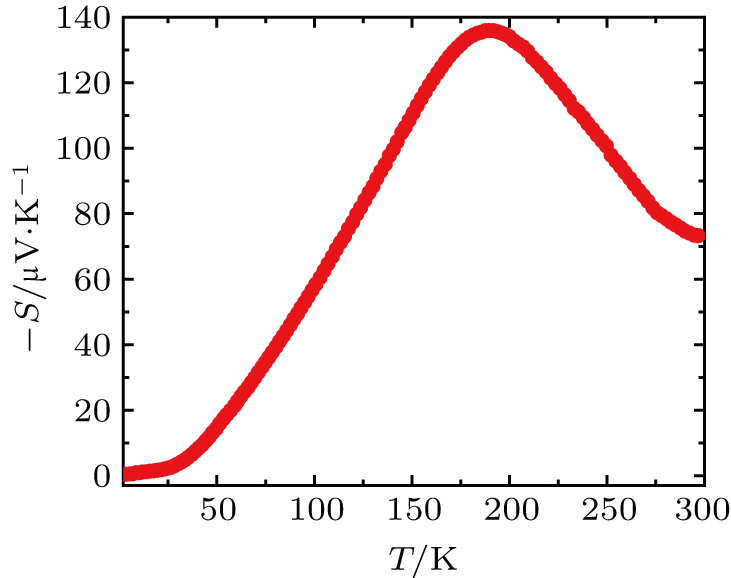
We have successfully grown an arsenopyrite marcasite type RhSb2 single crystal, and systematically investigated its crystal structure, electrical transport, magnetic susceptibility, heat capacity, and thermodynamic properties. We found that the temperature-dependent resistivity exhibits a bad metal behavior with a board peak around 200 K. The magnetic susceptibility of RhSb2 shows diamagnetism from 300 K to 2 K. The low-temperature specific heat shows a metallic behavior with a quite small electronic specific-heat coefficient. No phase transition is observed in both specific heat and magnetic susceptibility data. The Hall resistivity measurements show that the conduction carriers are dominated by electrons with ne = 8.62 × 1018 cm−3 at 2 K, and the electron carrier density increases rapidly above 200 K without change sign. Combining with ab-initio band structure calculations, we showed that the unusual peak around 200 K in resistivity is related to the distinct electronic structure of RhSb2. In addition, a large thermopower S(T) about –140 μV/K is observed around 200 K, which might be useful for future thermoelectric applications.
Many new 4d or 5d-electron based materials have been synthesized, and their exotic physical properties have been discovered and extensively studied in recent years. Compared to the 3d-electron based ones, they are less localized and have weaker correlation effects. But they have stronger spin–orbit coupling (SOC), which makes many of them novel topological materials or thermoelectric materials, such as WTe2, TaAs, ZrTe5, and HfTe5.[1–6] These materials have attracted extensive interests in the condensed-matter physics due to their non-trivial band topology and novel physical properties such as chiral thermal and electric transport behaviors. It has also been suggested that some narrow-gap semiconductors or semimetals of 3d-electron materials will have huge thermopowers like FeSb2 and CoSb2.[7–9] For example, FeSb2 crystallized in the marcasite-type orthorhombic structure was reported to be a narrow band nearly magnetic or Kondo semiconductor. The thermopower S(T) of FeSb2 could reach as high as 40 mV/K.[10] CoSb2 belongs to the pyrite-marcasite family. The thermopower S(T) of CoSb2 could reach 40 μV/K at room temperature.[9] We have noticed that RhSb2 crystallizes in arsenopyrite-marcasite type structure which is isostructural to that of CoSb2, and its powder sample was synthesized decades ago. However, its physical properties have not been well characterized so far. The room-temperature resistivity of the polycrystalline sample is 0.002 Ω⋅cm, and the thermoelectric power is reported to be +30 μV/K.[7] The magnetic susceptibility of RhSb2 shows Landau diamagnetism.[7,11,12] Therefore, to find new d-electron based materials with nontrivial topological band structure or exitonic physical properties is meaningful.
Transport properties are important for the application in devices as conducting materials. Generally, the resistivity of a normal metal increases with increasing temperature T because the phonon scattering of conducting electrons gets stronger at higher temperatures. For a semiconductor, the transport properties are dominated by the number of carriers, the resistivity decreases with increasing T due to the increased thermal activated carriers at higher temperatures. However, in some materials, the resistivity shows non-monotonic temperature dependences. For example, the temperature dependent resistivity of ZrTe5 or HfTe5 shows a broad peak around 65 K or 135 K.[13–20] It was explained either by a temperature induced Lifshitz transition observed in angle-resolved photoemission (ARPES) experiments,[21] or a topological band phase transition.[22] A sign change of thermopower Sxx is observed which might respond to the topological band structure.[23–25] Thus, it is of great interest to find similar transport behavior in other materials which may shed light in understanding the origin of the unusual transport behavior observed in ZrTe5 and HfTe5.
In this work, for the first time we successfully grew RhSb2 single crystals, and carried out detailed studies on its structure and basic physical properties, especially for the investigation of its unusual transport properties. We found that the temperature-dependent resistivity exhibits a bad metal behavior with a board peak around 200 K, which is similar to the situation in ZrTe5. The Hall resistivity measurements show that the conduction carriers are dominated by electrons, and the electron carrier density increases rapidly above 200 K. Combined with the electron band structure calculation, our analysis shows that the usual peak and the abruptly increases in carrier density around 200 K are related to the distinct electronic structure of this material. In addition, the magnetic susceptibility shows diamagnetism in the measured temperature range from 2 K to 300 K. The low temperature specific heat shows a metallic behavior with electronic coefficient of 1.09 mJ⋅mol−1⋅K−2. No phase transition is observed in susceptibility and specific heat data. Furthermore, we also carried the thermopower measurements and found that the thermopower is negative and its maximum absolute value |Smax| is about 140 μV/K at 200 K without any sign change in the whole temperature range.
Single crystals of RhSb2 were grown by self-flux method mentioned elsewhere.[9] The starting materials, Rh (99.99%) and Sb (99.999%, Alfa), were mixed together with the mole ratio 1 : 20 in Al2O3 capsules which were sealed into a quartz tube. The whole quartz tube was then quickly heated up to 1273 K in a furnace and maintained at this temperature for several hours. Then it was cooled down to 1073 K where the flux was spun off by a centrifuge. Finally, crystals with approximate dimensions 2 mm× 2 mm× 1 mm were left in the capsules. The crystals were stable in air and hydrochloric acid. To confirm the stoichiometry, the chemical compositions of the crystal were confirmed by energy dispersive x-ray spectroscopy (EDS) equipped on a Hitachi S-4800 scanning electron microscope (SEM). The crystals were characterized by x-ray diffraction (XRD) at 300 K on a Bruker SMART APEX II diffractometer using Mo Kα1 radiation (λ = 0.71073 Å). The crystal structure was refined by full-matrix least-squares fitting on F2 using the SHELXL-2014/7 program.[26] A well-crystallized sample was selected for the measurements. The magnetic susceptibility χ was measured in a Quantum Design SQUID VSM from 300 K to 2 K in field-cooling (FC) and zero-field cooling (ZFC) modes. The specific heat Cp was measured between 2 K and 300 K in a physical property measurement system (PPMS, Quantum Design) using a thermal relaxation method, approximately 12 mg of crystals were used for the specific heat measurements. The ρxx and the Hall coefficient data were measured upon cooling from 300 K to 2 K using a standard four-probe technique with a gauge current of 1 mA. Platinum wires and silver paste were used to make electrical contacts on RhSb2 single crystal. The angle dependent magnetic resistance data were collected with a lock-in technique at 2 K in the PPMS system. The first-principles calculations were performed using the Vienna ab-initio simulation package (VASP)[27,28] and the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE)[29] type exchange–correlation potential was adopted. We set 400 eV cutoff energy for the plane wave expansion and used 11× 11× 11 k-mesh for the Brillouin zone (BZ) in self-consistent calculations. The crystal structure from our EDS was exploited. The electronic structures both without and with spin–orbit coupling (SOC) were obtained.
RhSb2 crystallizes in a pyrite-marcasite type structure in space group P21/c (No. 14), as shown in Fig.
Figure
The large peak observed in ρ(T) at 200 K might be related to exotic physical mechanisms. To confirm whether the peak in the resistivity data is corresponding to a phase transition nor not, we carried out the magnetic susceptibility and specific heat measurements on RhSb2 single crystals. Figure
 | Fig. 3. (a) Temperature dependence of the dc magnetic susceptibility with ZFC and FC measured in a field of 1 T. (b) The magnetic hysteresis of the sample measured at 2 K and 300 K. |
Temperature-dependent specific heat (Cp(T)) of RhSb2 is presented in Fig.
 | Fig. 4. (a) Specific heat Cp as a function of T. (b) Cp/T versus T2 for a RhSb2 sample. The red line is the linear fitting data of Cp/T versus T2 at low temperature below 10 K. |
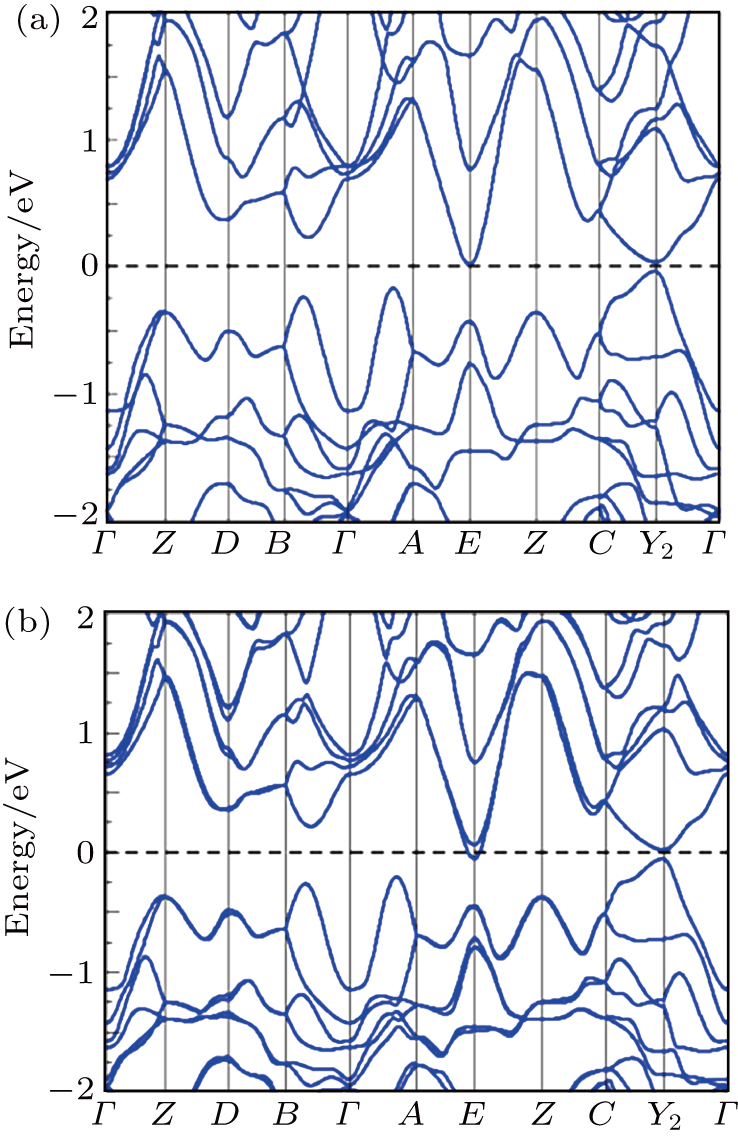
The above susceptibility and specific heat measurements suggest that the resistivity peak at about 200 K is not due to a phase transition. We find that such behavior may be understood by the distinct electronic structure in RhSb2. The band structure calculated within GGA is shown in Fig.
In order to check whether the temperature induced Lifshitz transition happened around 200 K in RhSb2, just like the situation in ZrTe5,[20,21] figure
Besides, we also studied the thermoelectric transport properties of RhSb2. As shown in Fig.
Similar ρ(T) with a peak at a certain temperature has also been observed in ZrTe5 and HfTe5 and the underline mechanism has been a puzzle for a long time.[14,17,18] Recently, it was proposed that a topological phase transition between strong and weak topological insulators might be the reason for it.[3] However, in ZrTe5 and HfTe5, the diamagnetism is strongly temperature dependent and S(T) changes sign around the peak of ρ(T).[16,25] These mean that RhSb2 is more like a narrow band gap semiconductor with a tiny electron pocket as shown in the GGA band structure. The small band gap around Y2 is tunable by strain or pressure effect. It is found that the critical uniaxial strain along c-axis and the hydrostatic pressure are both about 5% to drive the topological phase transition from a normal insulator to a strong topological insulator. Magnetic ion-doping can introduce spin dependent exchange interaction, which will compete with such small band gap and lead to topological states, such as magnetic Weyl semimetal and axion insulator.
We have successfully grown RhSb2 single crystal by Sb flux method. We present the structure, electron transport, heat capacity, magnetic, thermal transport properties of the bad metal d-electron compound RhSb2. The RhSb2 compound crystallizes into an arsenopyrite structure in space group P21/c. The temperature-dependent resistivity exhibits a bad metal behavior with a board peak around 200 K. The Hall resistivity measurements show that the dominate conduction carriers are electrons, and the electron carrier density increases rapidly above 200 K without any sign change. Together with the band calculations, we found that the unusual peak and abruptly increases in carrier density around 200 K are related to the topological electronic band structure of this material. In addition, the magnetic susceptibility shows diamagnetism in the measured temperature range from 2 K to 300 K. No phase transition is observed in susceptibility and specific heat data, which supports our calculations. Furthermore, we also carried the thermopower measurements and found that the thermopower is negative and its maximum absolute value |Smax| is about 140 μV/K at 200 K, which will be helpful for future device applications.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] |