Precise measurements of a weak radio frequency field with frequency less than 3 GHz play an important role in science, communication, and everyday life. Rydberg atom-based electric field sensor has achieved great progress in recent years due to its large electric polarizability (∝ n⁷) and big microwave-transition dipole moments (∝ n²).^[1] It covers the frequency range over from megahertz to terahertz, and has a potential to outperform the traditional electrometry due to the self-calibration characteristics. An all-optical sensing method based-on Rydberg electromagnetically induced transparency (Rydberg-EIT)^[2] and Autler–Townes (AT) splitting^[3] has been employed to character the properties of electric fields, including the measurements of microwave fields magnitude,^[4–6] polarization,^[7,8] phase,^[9] as well as millimeter waves,^[10] static electric fields,^[11,12] subwavelength imaging of microwave electric-field distributions,^[13,14] field inhomogeneities,^[15,16] and nonlinearity.^[17] Rydberg atoms have been also used as a radio frequency receiver for retrieving amplitude modulated (AM) base band signals that result in the “Rydberg atom radio”^[18–20] and can also be used to realize the extension of the feasibility of digital communication via a continuously tunable radio-frequency carrier.

A few techniques have been proposed for improving the sensitivity of weak field measurements, for example, (i) using high fineness optical cavities to narrow the EIT linewidth for improving the AT splitting resolution; (ii) using Mach–Zehnder interferometer detection^[21] and a frequency modulation technique^[22] to increase the signal-to-noise ratio; (iii) a Rydberg atom-based mixer has been used to realize the weak electric-field detection with sub-Hz resolution for the microwave field.^[23,24] In this work, we present a precise measurement of weak electric field in a room-temperature cesium vapor cell, where an atomic probe is employed to directly readout the weak radio frequency field that is encoded in the local microwave field. The RF field frequency of ∼ 2.18 GHz (∼ 1.32 GHz) couples a nearby Rydberg transition |68D_5/2⟩ → |69P_3/2⟩ (|80D_5/2 ⟩ → |81P_3/2⟩). The frequency of the weak signal electric field is hundreds of kHz different from the local field. The Rydberg-EIT is employed to directly detect the weak signal field, the corresponding minimum detectable field is ∼ 1.36 ± 0.04 mV/m (1.33 ± 0.02 mV/m) with a −3 dB measurement bandwidth of 3 MHz.

Experiments are implemented in a room-temperature cesium cell of length 50 mm and diameter 20 mm, as shown in Fig. 1(a), and the relevant Rydberg EIT-AT four-level diagram is given in Fig. 1(b). A probe and a coupling lasers overlap and counter-propagate through the cell. The weak probe beam, λ_p = 852 nm, is produced by an external cavity diode laser (Toptica DLpro) with a 1/e² waist of 100 μm at the cell center. The probe frequency is locked to the transition |6S_1/2 F = 4 ⟩ → |6P_3/2 F′ = 5⟩ using a super stable optical cavity (1.5 GHz FSR and 15000 fineness). The strong coupling laser, λ_c = 510 nm, is originated from a commercial laser (Toptica SHG110) with a 1/e² waist of 172 μm at the cell center, related frequency locked to the |6P_3/2F′ = 5 ⟩ → |68D_5/2⟩ Rydberg transition. Two radio frequency fields, denoted as local (E_L) and weak signal (E_S) fields with hundreds of kHz frequency difference, interact with the atoms simultaneously. Due to the small frequency difference between the two radio frequency fields and the small amplitude of the signal field, the electric field that atoms experienced is considered as the modulation of the local field,^[19] see details below. The power of the probe beam passing through the cell is detected with a photodiode (PD) and recorded with an oscilloscope. Both radio frequency electric fields have the polarization along z axis and parallel to the polarization of the probe and coupling beams.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. (a) Schematic diagram of experiments. The coupling and probe beams, forming a Rydberg three-level system, counter-propagate through a cesium vapor cell along the x axis. Two radio frequency fields with hundreds of kHz difference, denoted with solid and dashed arcs, interact with the three-level system. The one radio frequency field is denoted as a local field (EL) and the other one as a weak signal field (ES). The transmission of the probe is used to directly read out the signal field by a photodiode (PD) after a dichroic mirror (DM). (b) Energy level diagram. The probe (coupling) laser is resonant with the lower |6S1/2 F = 4⟩ → |6P3/2 F′ = 5⟩ (up |6P3/2 F′ = 5 ⟩ → |68D5/2⟩) transition. The local (signal) field with the frequency ∼ 2.18 GHz couples Rydberg transition |68D5/2⟩ → |69P3/2⟩. Small frequency difference between the two radio frequency fields results in the modulation to the local field, see text. (c) Measurements of Rydberg EIT-AT spectra as a function of the coupling laser detuning Δc with a local field EL = 0.49 V/m. The solid lines correspond to Lorentz fittings to the EIT-AT spectra. The extracted EIT linewidth is ΓEIT = 2π × (12.54 ± 0.13) MHz. The coupling frequency is continuously scanned by the SC110 module of a commercial laser Toptica SHG110 and the probe transmission spectrum is detected by a PD and recorded with an oscilloscope.

A local radio frequency field, generated with a function generator (SRS SG384) and emitted from a horn antenna, is applied transversely to the laser beams propagating through the vapor cell, where it interacts with cesium Rydberg atoms. The local field has a frequency ∼ 2.18 GHz (1.32 GHz), resonantly driving the |68D_5/2⟩ → |69P_3/2⟩ (|80D_5/2⟩ → |81 P_3/2⟩) Rydberg transition with Rabi frequency Ω_RF. A signal field with hundreds of kHz difference in frequency from the local field, is originated from another function generator (Keysight N5183B) and emitted by another antenna. The local field causes an AT splitting of the Rydberg-EIT illustrated in Fig. 1(c) as a function of the coupling laser detuning. The Lorentz fitting to the field-free EIT spectrum yields linewidth Γ_EIT = 2π × (12.54 ± 0.13) MHz. An observed EIT transmission splits into two peaks, EIT-AT splitting f_AT, in the presence of local field E_L. Analysis of the Rydberg-EIT-AT spectra reveals the Ω_RF value, which is proportional to the radio frequency electric field. Hence, this spectroscopic method affords an all-optical readout of the time-dependent field strength. The extracted f_AT is 2π × 15.89 MHz by using multi-peak Lorentz fittings to the data (red solid line), corresponding local electric field E_L = 0.49 V/m. In following experiments of weak signal field measurements, the local field is set to this value. The coupling laser frequency is locked to the up transition |6P_3/2 F′ = 5 ⟩ → |68D_5/2⟩ (|80D_5/2⟩) and the Rabi frequencies of the probe and coupling beams are Ω_p = 2 π × 13.35 MHz and Ω_c = 2 π × 2.94 MHz, respectively.

Microwave field measurement based on Rydberg EIT-AT splitting is no longer applicable for the weak electric field when the field induced AT splitting is less than the EIT linewidth, f_AT ≲Γ_EIT. To detect the weak field, we encode this weak field, considered as a signal field , to a strong local field (). Both the weak signal and strong local fields incident on to the vapor cell simultaneously. Such that the radio frequency field the atoms experienced in the path of the probe and coupling beams is written as

For the signal field with its polarization being parallel to the local field and the frequency difference satisfying the condition of , , the scalar total microwave electric field that the atoms feel can be expressed as

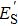
The probe-power transmission is P = P₀exp(−α L), with the probe-laser absorption coefficient α = 2πIm(χ)/λ_p and L the vapor cell length. The χ is the susceptibility of the medium seen by the probe laser. The χ is written as

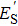
In a preliminary experimental test, we set local field frequency ω_L = 2π × 2.185740 GHz that couples the nearby Rydberg transition |68D_5/2 ⟩ → |69P_3/2⟩. The local field results in the AT splitting, f_AT = 2π × 15.89 MHz, that is close to the EIT linewidth, see Fig. 1(c). The weak signal field frequency ω_S = 2π × 2.185780 GHz with frequency difference Δω = 2π × 40 kHz relative to the local field. Figure 2 presents the measured probe laser transmission for three indicated radio frequency E_S fields under two photon resonant Rydberg-EIT. The probe laser transmission shows a nice sinusoidal profile with a frequency 40 kHz. We fit the spectra of Fig. 2 with sine function to extract the amplitude . It is clearly shown that the probe transmission amplitude decreases when the signal intensity E_S decreases, the corresponding signal fields are 0.08 V/m, 0.13 V/m, and 0.18 V/m, respectively. The values of electric field can be acquired by calibrating the probe transmission amplitude with an EIT-AT spectrum discussed below.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Measurements of the probe laser transmission with an indicated weak signal field ES = 0.18 V/m (bottom), 0.13 V/m (middle), 0.08 V/m (top) in the presence of the local field EL = 0.49 V/m at two photon resonant Rydberg-EIT. The transmission shows a nice sinusoidal profile, the related amplitude increases with the signal field ES.

When the signal field decreases further, the detected probe transmission displays a deformed sine profile that can not be well fitted with a sine function. To read out the amplitude of weak field E_S, we employ a lock-in amplifier triggered by the beat signal that is obtained with a radio frequency mixer. The output of the lock-in amplifier is proportional to the amplitude of signal field E_S. To do the test, we decrease the signal electric field and do a series of measurements, corresponding electric fields displayed with red squares in Fig. 3(a) for ω_L ∼ 2π × 2.18 GHz. The inset of Fig. 3(a) displays the output of the lock-in amplifier. To calibrate the electric field value, we use the Rydberg EIT-AT spectra at strong field range with the formula f_AT = Ω_RF = μ E_RF/ħ, in which Ω_RF (μ) denotes the Rabi frequency (dipole matrix element) the radio frequency field coupled and ħ is the reduced Planck constant. The measured strong electric field is shown with blue circles in Fig. 3(a). The radio frequency field is proportional to the square root of the output power of the function generator^[25]

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. Measurements of the lock-in output of the probe transmission (red squares) and signal fields ES (blue circles) by EIT-AT spectra versus the square root of the output power, , of the function generator for (a) signal field frequency ωS ∼ 2π × 2.18 GHz and (b) ωS ∼ 2π × 1.32 GHz. The black line is the calculation of equation . The detectable minimum of signal field ESmin = 1.36 ± 0.04 mV/m in (a) and 1.33 ± 0.02 mV/m in (b). The error bars display the standard error of two independent measurements. The inset demonstrates the lock-in output of the probe transmission.

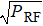
Finally, we measure the bandwidth of the signal field. We change the frequency of the signal field while keep the local field fixed and do the similar measurements of Fig. 3. Figure 4 presents the measurements of electric field, 20log(E_S/E₀), as a function of the signal field frequency for two different field values, E_S = 0.39 V/m (black circles) and 0.07 V/m (red triangles), respectively. The −3 dB bandwidth is about 3 MHz, which depends on the photodiode detector used.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Measurements of signal electric field, 20 log ES/E0), as a function of Δω by changing the signal field frequency for two indicated signal field values ES = 0.39 V/m (black circles) and 0.07 V/m (red triangles), respectively. Horizontal dot-dashed line displays the idea −3 dB line, related −3 dB bandwidth of 3 MHz, depending on the photodiode used.

In summary, we have presented a weak electric field measurement for a frequency ω_S ≲ 2π × 3 GHz employing a resonant atomic probe. When the signal field is much weaker than the local field, E_S ≪ E_L, the two-photon resonant Rydberg EIT displays a sine profile with frequency difference of the local and signal fields, Δω, and sine amplitude of . This sine profile of the probe transmission yields a fast and direct readout of the signal radio frequency electric field. The measured minimum fields of 1.36 ± 0.04 mV/m and 1.33 ± 0.02 mV/m are attained for two selected test RF frequencies of 2.18 GHz and 1.32 GHz, respectively. The resonant atomic probe provides a method of fast and direct readout the field value without further processing and the related radio frequency easily extends to tens of GHz. Furthermore, this method can be used to measure the radio frequency electric field with signal frequency being continuously varied, arriving at −3 dB bandwidth of 3 MHz in this work. The bandwidth can be a few MHz depending on the optical detector used. The measured accuracy could be improved by one order of magnitude by compressing the laser frequency and intensity noise. Compared to the previous field measurements,^[21,22] the method of this work is simple and provides a rapid and precise way to measure the weak radio frequency electric field.