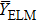† Corresponding author. E-mail:
Project supported by the National Key R&D Program of China (Grant Nos. 2017YFE0300400 and 2017YFE0301300), the National Natural Science Foundation of China (Grant Nos. 11475223 and 11775257), the National Magnetic Confinement Fusion Science Program of China (Grant No. 2015GB101003), and also partly supported by AHNSF of China (Grant No. 1808085J07).
During edge localized modes (ELMs), the sheath evolution in front of the Experimental Advanced Superconducting Tokamak (EAST) upper divertor is studied to estimate the sputtered tungsten (W) atoms from the divertor target. A large potential drop across the sheath is formed during ELMs by compared with inter-ELMs, and the maximum of sheath potential drop can exceed one thousand of eV in current EAST operation. Due to the enhancement of the sheath potential drop during ELMs, the W physical sputtering yield from the deuterium (D) ions and the impurity ions on the upper divertor target is found to be significant. It is established that the sputtered W yield during ELMs is at least higher by an order of magnitude than inter-ELMs, and D ions and carbon (C) ions are the main ions governing the W production for the current H-mode with ELMs discharges. With increase in the pedestal electron temperature, the maximum of the D and C ion impact energy during ELMs shows a nearly linear increase, and the D ions have sufficient impact energy to cause the strong W physical sputtering. As a consequence, the D ions may dominate the sputtered W flux from the divertor target when the C concentration is controlled less than one percent for the higher heating power H-mode with ELM discharges in near future.
The edge localized modes (ELMs) driven by the quasi-periodic magnetohydrodynamic instabilities are often observed in tokamak plasmas with the high-confinement mode (H-mode). ELMs will cause the transient energy loss of the plasma stored energy and expel the impurities from the main-edge plasma region before they penetrate the core plasma. Most of the particle and energy fluxes induced by ELM bursts are transported to the divertor regions and then lead to the excessive heat load on the divertor plate and strong ion impact energy on the divertor material. As a consequence, the impurity releases from the divertor plate and the resultant lifetime of the material decreases. Furthermore, the impurity from the divertor target can migrate into the core plasma to deteriorate the plasma confinement. Hence, the ELM event and a series of problems induced by ELMs may limit the H-mode operation regime. With low sputtering yield and high melting point, tungsten (W) material has been used as the divertor target material in several tokamaks,[1–3] and it is also suggested as the divertor target material instead of carbon (C) in next fusion devices such as ITER and CFETR.[4] In the Experimental Advanced Superconducting Tokamak (EAST), the upper graphite divertor was upgraded into a full W one with ITER-like actively water-cooled monoblock structure in 2014.[3] With upper W divertor, the EAST obtained over 60 s in fully noninductive H-mode plasma operation in 2016.[5] However, under some conditions, the W from the upper divertor can degrade the plasma confinement and even cause the termination of the plasma discharge.[6] Since the core plasma has a very low tolerability to the W concentration,[7] the control of W production and W radiation are the key issues for long-pulse high performance operation in the EAST.
The physical sputtering is the main process of W production. In this process, the sheath plays a crucial role in determining the W physical sputtering since it can change the ion bombardment energy on the W material. For a collisionless sheath, the ion impact energy on the material is determined by the ion energy at the sheath edge and the ion acceleration across the sheath. In L-mode or inter-ELM H-mode deuterium (D) plasma operation, the potential drop across the sheath Φ approximates to −e0 Φ ≈ 3kB Te,0 with the elementary charge e0, the Boltzmann’s constant kB and electron temperature near the divertor Te,0. During the ELMs, Φ depends on the pedestal electron temperature.[8–10] Based on the sheath evolution obtained from the analytical model during ELMs, it is shown in the JET that the D ion is the main trigger of the W source while the contribution of the beryllium ion is lower by an order of magnitude because of the small concentration.[11] In the current EAST, H-mode discharges with upper W divertor configuration have been operated with the mixed wall materials and lithium (Li) coating.[5] The W production caused by multiple impurity ions must be estimated. For the L-mode discharges, it was found that the W erosion is governed mainly by C ion bombardment instead of molybdenum (Mo) from the first wall material.[12,13] For the H-mode with ELMs discharges, the W erosion and transport during the ELMs have been investigated.[14,15] However, effect of the multiple impurity ions on the W production with the sheath evolution during ELMs is not taken into account.
In this work, we perform the evolution of sheath potential in front of the upper divertor in the EAST during an ELM pulse, and then discuss the following questions: What is the main element to determine the sheath potential? How much is the sputtered W yield by the multiple ion bombardment in current discharges? How do the contribution of the D ions and C ions to the W source vary with the input power? All these questions are related to the impurity control and plasma confinement. The rest of this paper is organized as follows: The models for the ELM and the sheath are described in Section
The ELMs transport in scrape-off-layer (SOL) can be described by the analytical model,[8,16] the Vlasov model,[16,17] particle-in-cell (PIC)[9,10] and fluid models. The ‘free-streaming’ kinetic model (FSM) describes ELMs as a quasi-neutral plasma bunch expanding along the magnetic field lines into the SOL without collisions.[8] It is shown that the results of the particles and energy fluxes on the divertor target obtained by the FSM agree well with the collisionless Vlasov model[17] and the ion impact energy of the peak power density at the strike point predicted by the FSM matches the JET experimental result.[11]
In the FSM, the parallel temperature is constant in space and given by[8]
 |
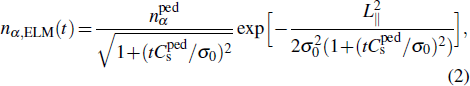 |
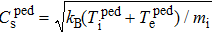
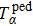

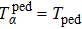
In the EAST, the timescale of the ELM usually is ωELM ≈ 105–107 s−1. Near the divertor region, the typical plasma density at sheath edge during inter-ELMs, i.e., background density, 
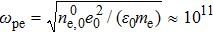
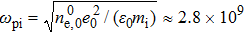
 |
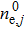
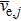
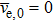
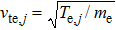
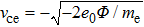
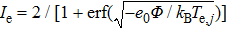
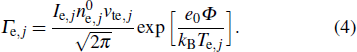 |
 |
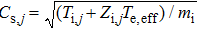
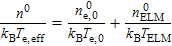
The Φ is obtained based on the zero current to the target surface,
 |
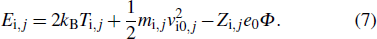 |
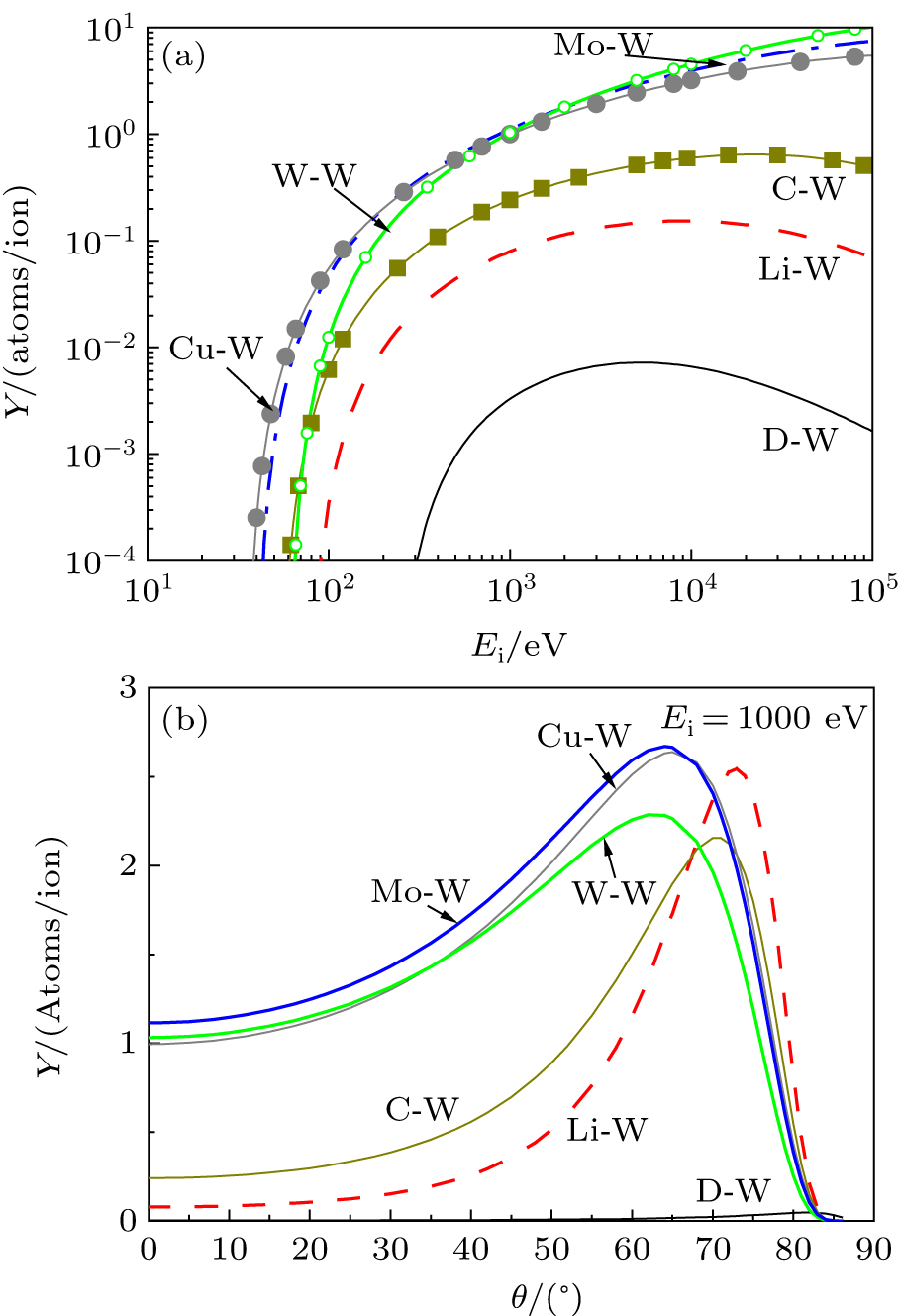
When the plasma hits the W target, W is mainly produced by physical sputtering process. Here the empirical formulas proposed by Yamamura is used to calculate the physical sputtering yield for the normal incidence of a projectile on a target[24]
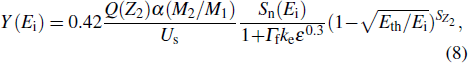 |
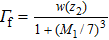
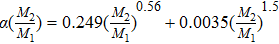
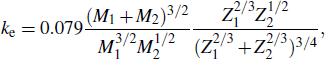 |
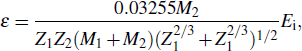 |
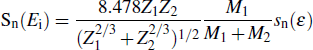 |
For the angular dependence of the physical sputtering, the calculated yield values at a given incident energy are calculated by another Yamamura formula[25]
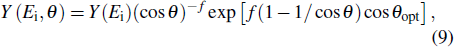 |
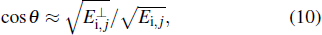 |
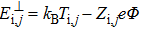
For the typical H-mode discharge with ELMs in the current EAST, L∥ = 20 m, B ∼ 2 T and the angle between magnetic field lines and divertor target plate is 5°. In the divertor region, 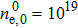
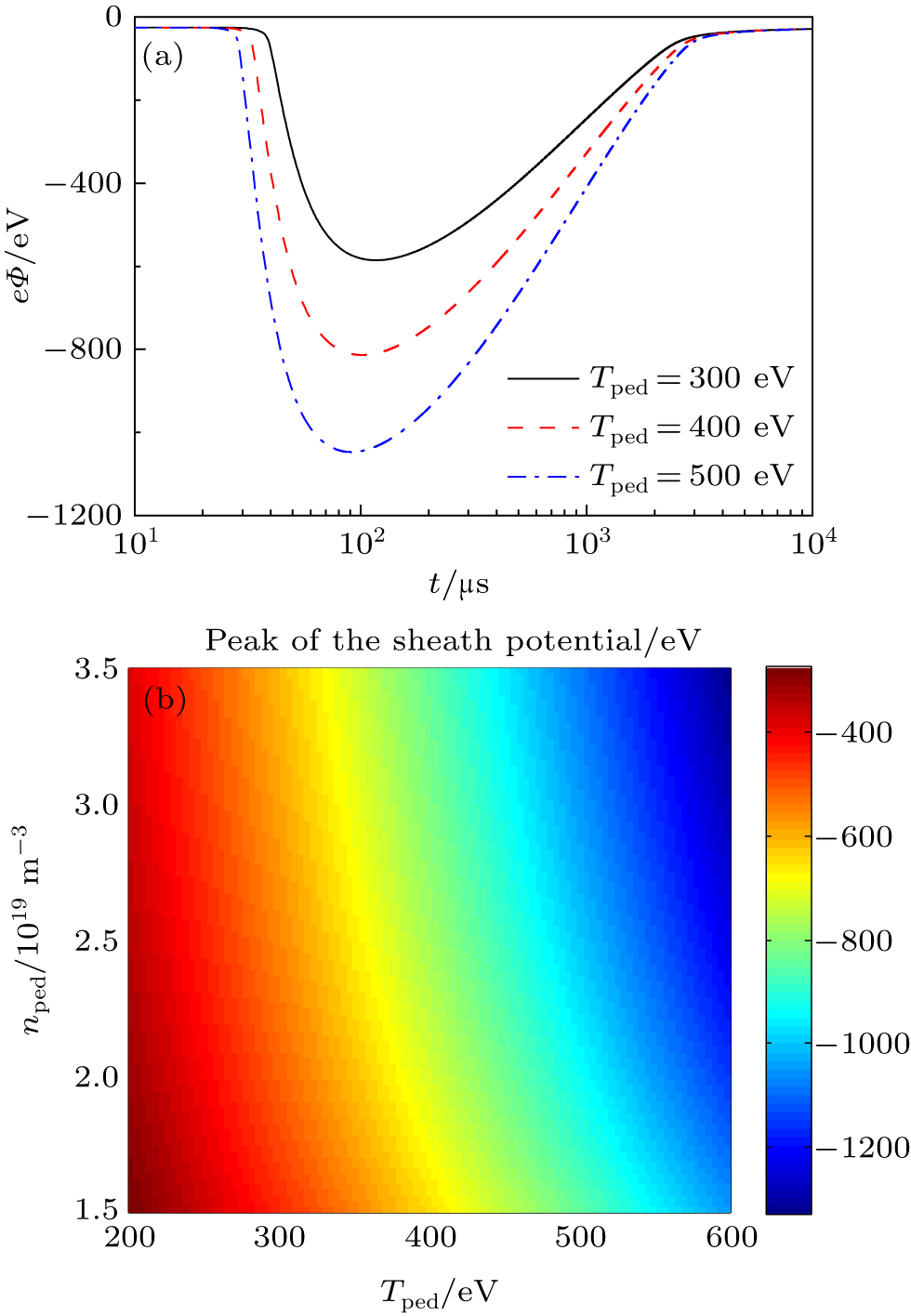
Firstly, we investigate how the sheath potential is changed by the ELM. Figure
 | Fig. 2. The time evolution of the plasma density at the sheath edge due to ELMs (a), particle fluxes at the target (b), and the sheath potential (c) for nped = 2 × 1019 m−3 and Tped = 480 eV. |
Effect of the pedestal temperature on the evolution of the sheath potential is shown in Fig.
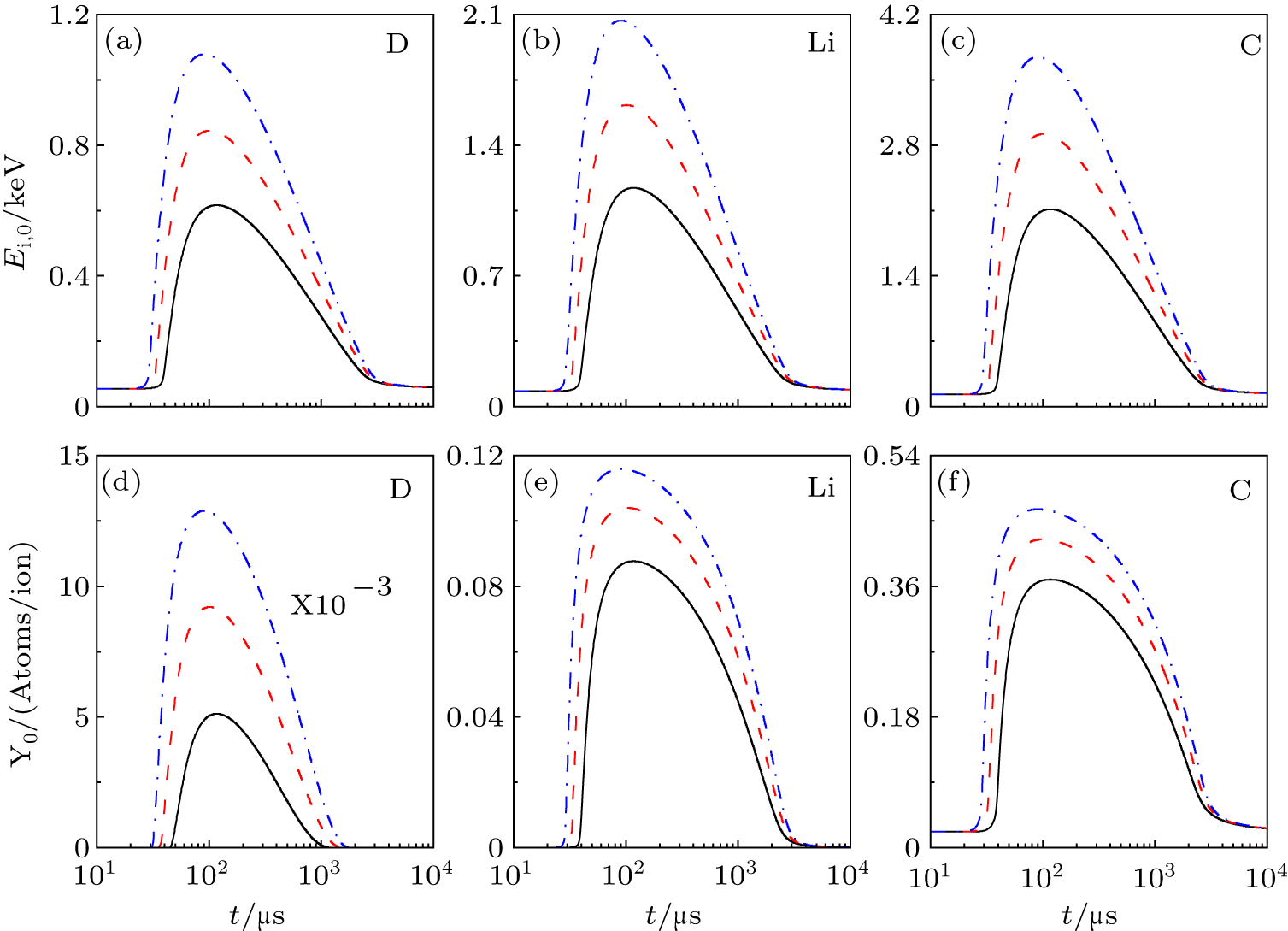
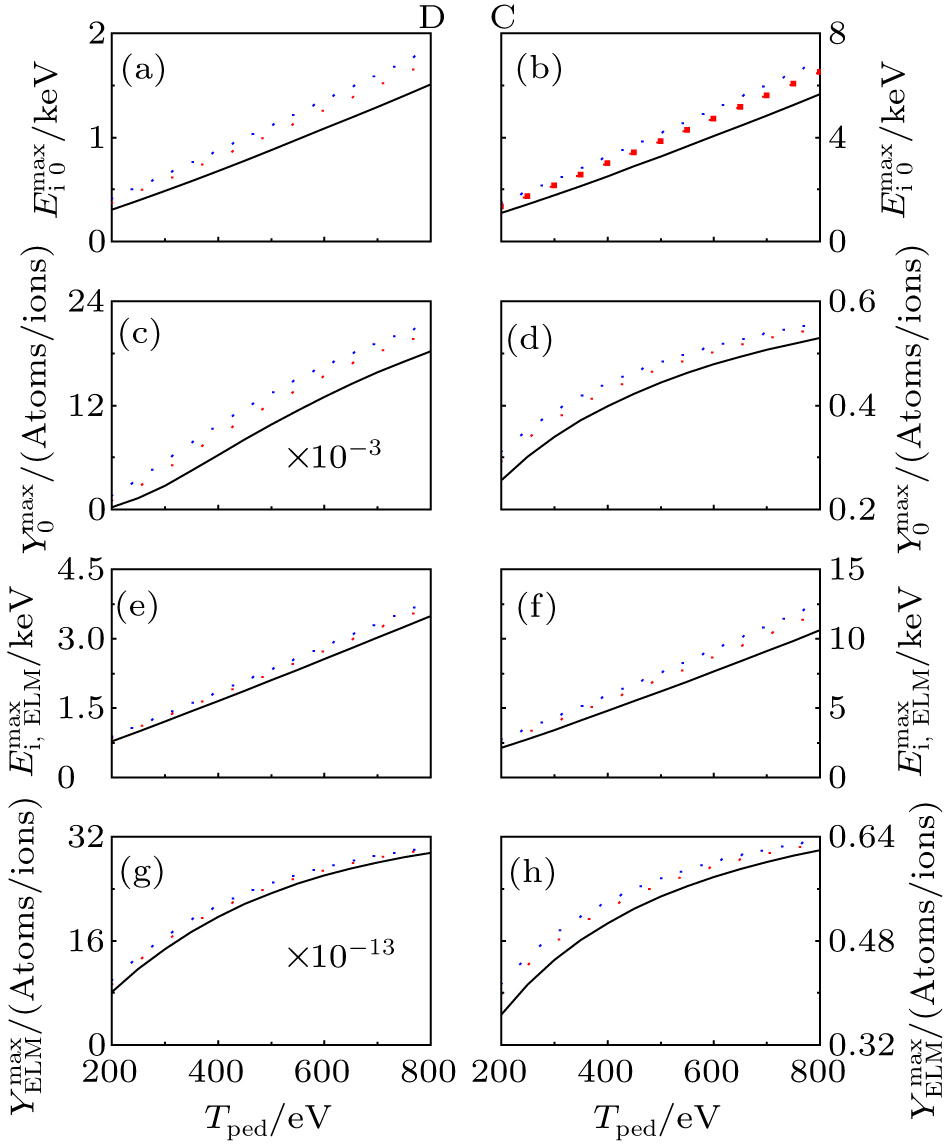
The ion impact energy on the divertor target can be increased during ELMs as a result of the enhancement of the sheath potential drop. It is the decisive parameter for the physical sputtering to cause W production. In the EAST, besides the main ions of D, the impurity ions from the mixed wall materials and Li ions due to wall coating also impact on the divertor target and are the potential contributors causing the W production. To investigate the W production from upper divertor during ELM, we show the evolutions of the W physical sputtering yields caused by background D ions and common impurity ions including Li, C, Cu, Mo W, and the corresponding ion bombardment energies in Figs.
To estimate the W production in a whole ELM pulse, we assume that the effect of the ELM on the divertor target from 30 μs to 3000 μs based on Fig. 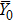
| Table 1. The averaged sputtered W yield caused by background multiple ions. . |
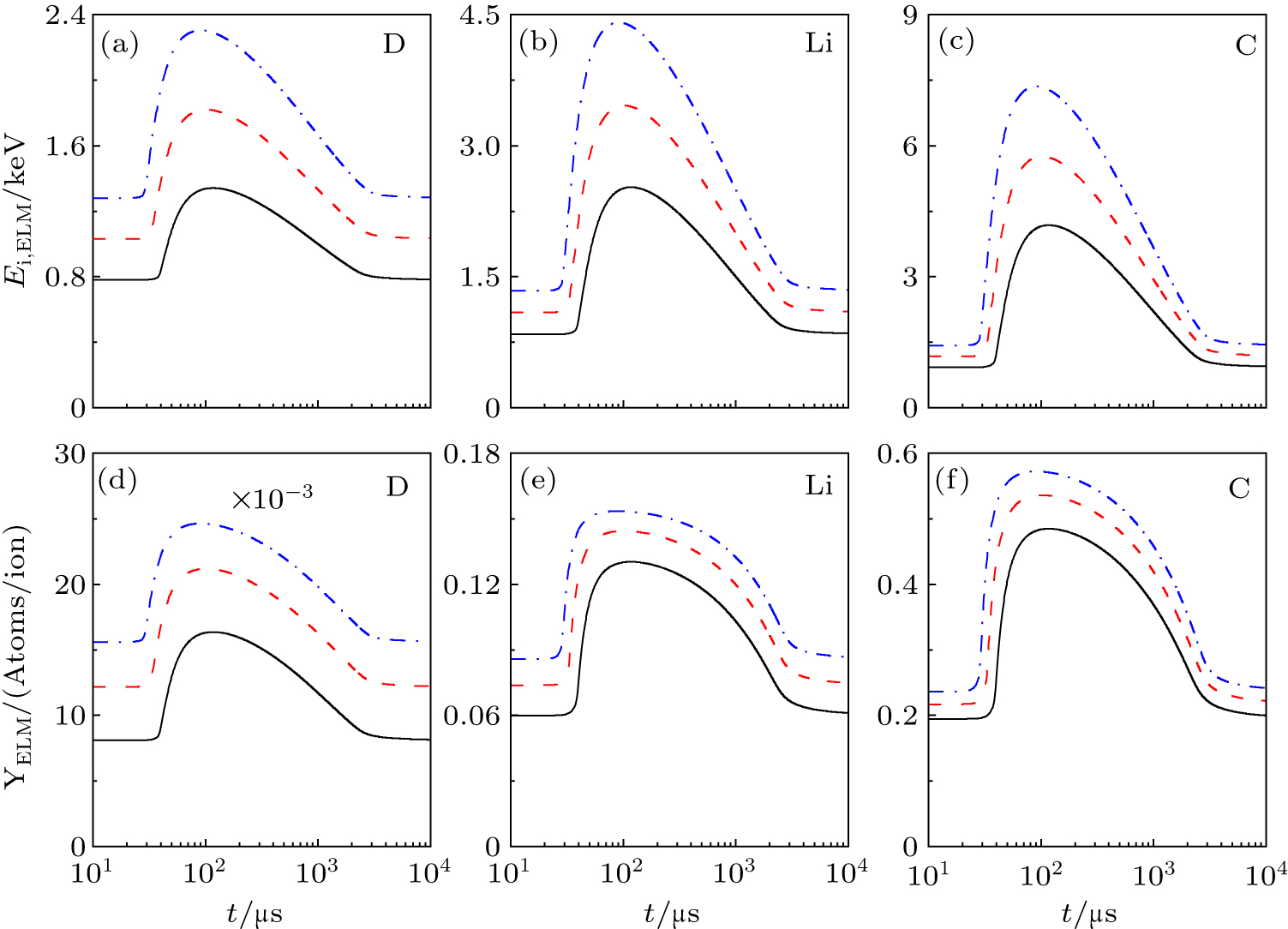
During ELMs, D ions and impurity ions in the pedestal region can be expelled by ELMs to the SOL and then impact on the divertor target. Due to the high ion energy at sheath edge, these hot ions have more higher impact energy than background ions. Since the concentration of the heavy metal impurity is very small in the core region, here we only investigate W sputtering yield from the D, Li and C ions carried by ELMs on the divertor target. Figure
From Table 
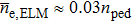
| Table 2. Averaged sputtered W yield |
Finally, we discuss the variation of the ion impact energy and the corresponding W sputtering yield with the pedestal temperature. In the JET, the experimental results have shown that the main ion impact energy depends linearly on the pedestal temperature.[11] In the current EAST, the sputtered W yield from C ions on the divertor target should not be ignored since C impurity is the main contributor for the W source. Here we investigate the dependence of maximum impact energy of the D ions and C ions on the pedestal temperature. For both background ions and hot ions carried by ELMs, it is shown in Fig.
During ELMs in EAST H-mode discharges, the transient enhanced energy deposition on the upper divertor target can cause the strong W physical sputtering. To estimate the sputtered W atoms from the divertor target, the evolution of the sheath potential in an ELM pulse is investigated with the ‘free-streaming’ kinetic model which describes ELMs. The large potential drop across the sheath can be formed in front of the divertor target during ELMs by compared with inter-ELMs. It is found that the maximum of sheath potential drop depends on the arrival of the pedestal bulk plasma temperature and density, and it can exceed one thousand of eV in the current EAST operation.
For the current operation in the EAST, with the enhancement of the sheath potential drop during ELMs, the background D ions can obtain the impact energy beyond threshold energy and then become one of the contributors causing the W production. For the background impurity ions such as Li, C, Cu, Mo and W, the maximum of sputtered W yield caused by their bombardment increases by one order of magnitude compared to the inter-ELMs. The results also show that the averaged sputtered W flux caused by D ions during ELMs is comparable to that caused by C ions since the C ion concentration is more than one percent in the current EAST upper dvertor region. It is suggested that C and D ions are the main ions governing the sputtered W flux from the upper divertor target during the ELMs burst. However, with increase in the heating power in near future, the W physical sputtering yield from background D ions on the divertor target surface increases rapidly due to the increase in the pedestal temperature. The averaged sputtered W flux caused by D ions may be larger than that caused by the C ions if concentration of C ions is less than one percent, and then the D ion becomes the potential main trigger of the W source for high heating power discharges in near future. Finally, it should be noted that in the present work, we focus on the W production while neglect the energy reflections and W re-deposition processes. In the further works, the effect of the magnetized sheath on the energy reflection and W re-deposition will be included.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] |