† Corresponding author. E-mail:
Optical features of a semiconductor–dielectric photonic crystal are studied theoretically. Alternating layers of micrometer sized SiO2/InSb slabs are considered as building blocks of the proposed ideal crystal. By inserting additional layers and disrupting the regularity, two more defective crystals are also proposed. Photonic band structure of the ideal crystal and its dependence on the structural parameters are explored at the first step. Transmittance of the defective crystals and its changes with the thicknesses of the layers are studied. After extracting the optimum values for the thicknesses of the unit cells of the crystals, the optical response of the proposed structures at different temperatures and incident angles are investigated. Changes of the defect layers’ induced mode(s) are discussed by taking into consideration of the temperature dependence of the InSb layer permittivity. The results clearly reflect the high potential of the proposed crystals to be used at high temperature terahertz technology as a promising alternative to their electronic counterparts.
Nowadays we are witnessing increasing progresses in different branches of the laser and photonic technologies which are pointing towards the rapid transitions from pure science to experiments.[1–5] However, these successes are not just related to the advancements in the fabrication techniques alone. Foundation of new materials and suggestions of more applicable elements have become very influential in these regards. Photonic crystals (PCs) are undoubtedly one of the structures that many advancements could be related to. The idea of using two/more dielectrics stacked periodically in one, two, or three dimensions for manipulation of the electromagnetic waves propagation is not a new idea.[5–7] There exist numerous reports in which optical features of various kinds of these structures have been investigated.[8–13] They have been widely proposed in fabrications of not only light sources such as lasers/diodes[14,15] but also detectors and transducers,[15] all optical filters, mirrors, and switches.[16–26] Nevertheless, these structures are still on tops of attention for new photonic elements design due to their unique characteristics. Valuable experimental techniques including chemical/optical methods and various deposition approaches are also suggested for their fabrication.[24,25] Laser technology has been also applied in this regards following its great successes in material surface patterning.[26,27]
Needs for tunable components in new generations of optical integrated circuits (OICs) reflect the importance of the PCs even more evident. This has been an important issue over the last few years for researchers and manufacturers of photonic technology. Different structures have been suggested in this regards by benefiting the temperature dependence of the refractive index of a specific material,[28] crystals with electro/magneto optical features,[29] or using some materials with efficient response to external mechanical tensions.[30] One could also refer to the valuable Refs. [30]–[37] for other novel structures with applications in the visible–infrared range.
In the light of these valuable reports, here in this paper we propose new structures with interesting optical responses in terahertz (THz) frequency range. The suggested crystals have some advantages such as using layers of well-known SiO2 and InSb materials with reasonable thicknesses and having sensible numbers of periods which are very vital from experimental points of view. Thus, it seems that their fabrication is completely possible in reality. The paper is organized as follow: the mathematical approaches are introduced at first. The one-dimensional (1D) ideal crystal composed of periodic layers of SiO2 and InSb is presented next and then its optical features are explored comprehensively. Special attention is paid to the dependence of the photonic band gap (PBG) on the layers’ thickness. In addition, selecting the optimum widths, two different defective structures are considered and the induced variations in the PBG and transmission spectrum are studied. Then, tunability of the optical features of the structures is extensively investigated by taking into consideration of the crystal thermal response. The results are discussed by focusing on the well-known physical facts. At last, the dependence of the proposed crystals’ transmittance on the wave incident angle is explored.
The incident plane wave on the interface of two isotropic media splits into two parts (reflected and transmitted waves). The incident (i), transmitted (t), and reflected (r) plane waves can be defined as
 |
 |
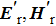
 |
 |
 |
 |
 |
 |
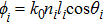
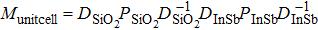
 |
Similarly, for two proposed defective structures illustrated in Fig.
 |
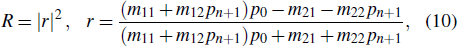 |
 |
 |
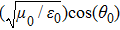
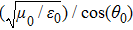
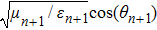
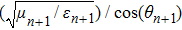
Thermal fluctuations can lead to various linear/nonlinear optical and physical phenomena. Refractive index changes and material size variations are two famous effects in this regards. Thus it is necessary to include all these dependencies in the calculations to increase the accuracy of the simulations. The temperature dependence of the constituent layers’ thicknesses due to the possible thermal expansions can be considered as[38]
 |
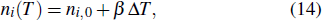 |
Being as one of the main building blocks of the proposed PCs, before discussing the results, it is worth to review the thermo-optical features of the InSb semiconductor in more details. It has been proven that its relative permittivity is dependent on the temperature and frequency and can be described by the Drude model[38]
 |
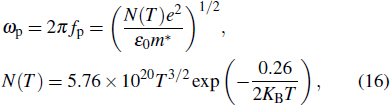 |
 |
Figure
Dependence of the optical features of the ideal crystal (without any defect) on the thicknesses of the layers is studied at the first step. Numerical constants are taken as εSiO2 = 2, dSiO2 = 4 μm, dInSb = 4 μm, αSiO2 = 5.5 × 10− °C−1, βSiO2 = 10−5 °C−1, m* = 0.015 m0, and m0 = 9.1 × 10−31 kg in the simulations. The photonic band structures of the crystal composed of 8 periods of SiO2/InSb layers are presented in Fig.
Transmittance spectra of the ideal crystal without any defect inside its structure and the first and second defective PCs are presented in Fig.
For the FDPC, the intensity (height) of the mode in the second gap (> 80%) is much higher than that in the first PBG (< 60%). Similar relation is observed between the first and the third modes of the gaps in the spectrum of the SDPC (the numbering is from low to high frequencies). But the ratio of the second modes of the gaps is different and the 4th mode in the second gap has lower intensity than the 2nd one in the first PBG.
It is clear that the wide PBGs and the sharp resonant peaks of ∼ 100% transmittance inside the gaps might find various applications in the fabrication of photonic devices such as optical filters, switches, wavelength samplers, etc. Thus the dependence of the optical features of the proposed crystals on the thicknesses of the layers is studied more systematically in order to find the optimum thicknesses for those applications. Figures
Tunability of the optical features of the proposed crystals is studied in the next step. Figure
As the temperature increases, the whole transmittance spectrum of the SDPC blue shifts similar to what takes place for the SDPC. As a result, all the modes shift to higher frequencies with increasing temperature. The intensity (height) of the modes reduces. But the variations are not the same for all the modes. The first mode experiences the largest variations and the second and third ones show the lowest changes. It is worth noting once more that the numbering of the modes is from left side of the spectrum to the right (lower frequencies to higher ones). Except the first mode with transmittance of ∼ 40% at 310 K, all other modes have values higher than 70% even at room temperature. This reflects the potential of this structure and its successful performance at high temperatures without any need to cool the systems.
The interesting temperature dependence of the optical features might be related to the changes of the refractive index of the InSb layer with temperature. At terahertz frequency range, the refractive index of InSb is complex valued and temperature dependent as shown in Eqs. (
Increase in the extinction coefficient results in more loss and thus the reduction of the crystal transparency. This is in consistence with the results presented in Figs.
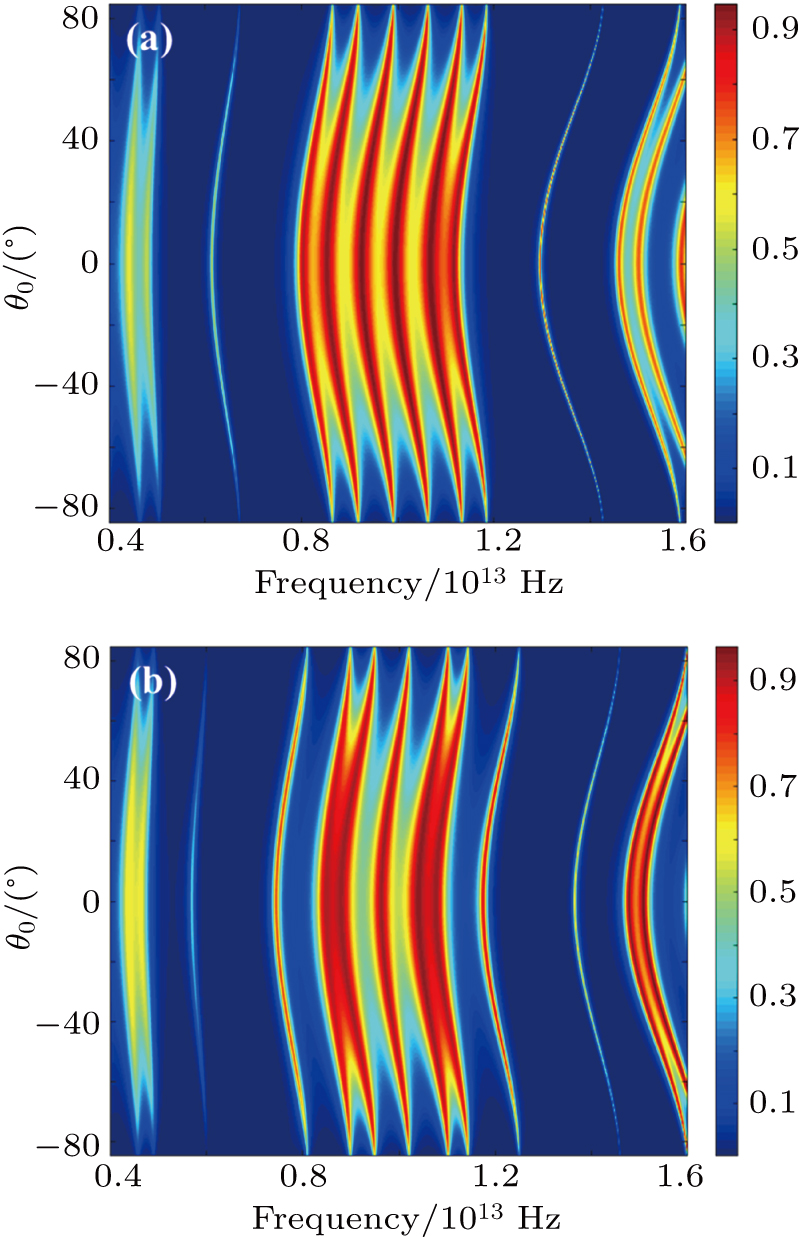
Finally, the dependence of the optical features of the proposed defective crystals on the wave incidence angle is investigated by exploring the changes of these crystals’ transmittances. Figures
In order to further discover the sensitivity to temperature and incident angle, the band gap widths are extracted and tabulated in Tables
| Table 1. Width of the 1st and 2nd stop bands of the FDPC structure at various temperatures and incident angles. . |
| Table 2. Width of the 1st and 2nd stop bands of the SDPC structure at various temperatures and incident angles. . |
One-dimensional ideal photonic crystal consisting of micrometer sized SiO2/InSb alternating layers was proposed for terahertz applications. Optical response of two more defective structures (FDPC and SDPC), which are producible by disrupting the ideal crystal regularity, were also explored systematically besides the perfect PC. The results show that by changing the layers’ thicknesses, a shift in the dispersion curve of the ideal crystal is observed. So that with increasing the thicknesses of the layers, the PBG intervals red shift and new gaps are generated at higher frequencies. The amount of changes is dependent on the amount of thickness changes. Inserting intentional defects in the crystal structure results in generation of the resonant mode(s) in the PBGs. Furthermore, the size of the gaps is also increased (compared to the ideal crystal) but the number of modes is different for the FDPC and SDPC. The width, central frequency, and the number of the PBGs of both defective crystals are seriously dependent on the thicknesses of the layers. In the case that the layers’ thicknesses are the same, alterations of the crystals transmittance with the thicknesses of the unit cells are more predictable. In other words, the PBG intervals experience red shifts with rising the thicknesses of the layers and the central frequency of the defect layer(s) induced resonant modes also shifts continuously to the lower frequencies as a result. A blue shift in the total spectra of both the FDPC and SDPC structures is observed with increase in temperature and as a result defect modes shift to higher frequencies and their height (intensity) reduces. The central frequencies of all the modes are tunable with temperature. However, the dependence of different modes on temperature is different and the modes at lower frequencies are affected to some extent more. Both the proposed defective structures have a considerable response at temperatures as high as 300 K. Furthermore, the optical response of the crystals might be well controlled by adjusting the crystal orientation respect to the wave propagation direction. So that at entire of the selected temperatures, deviation of the incident beam from normal (in positive/negative directions) results in an increase in the width of the gaps. However, at large angles, temperature dependent changes of the PBG width become samller. In other words, as the temperature changes in the range of 225–310 K, the largest amount of variations (∼ 27%) in PBG width belongs to the case that the light incidence is normal.
The followings are the advantages/excellences of the proposed structures: (i) optical response in terahertz frequency range, (ii) being made of common semiconductor and dielectric materials (not including materials such as graphene layers which are hard to be purely synthesized), (iii) reasonable layer thicknesses (in micrometer range, which is much easier to be fabricated compared to the nanometer sizes), (iv) low numbers of layers, (v) response in a wide range of incident angles and presenting almost omnidirectional band gaps, (vi) easy and effective tunability of the optical responses, (vii) good performance at high temperatures without additional cooling systems. Thus it seems clearly that these crystals might be affordable for terahertz technology in practice.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] |