† Corresponding author. E-mail:
Recent studies in van der Waals coupled two-dimensional (2D) bilayer materials have demonstrated a new freedom for material engineering by the formation of moiré pattern. By tuning the twist angle between two layers, one can modulate their electronic band structures and therefore the associated electrical transport and optical properties, which are distinct from the original ones of each individual layer. These new properties excite great passion in the exploration of new quantum states and possible applications of 2D bilayers. In this article, we will mainly review the prevailing fabrication methods and emerging physical properties of twisted bilayer materials and lastly give out a perspective of this topic.
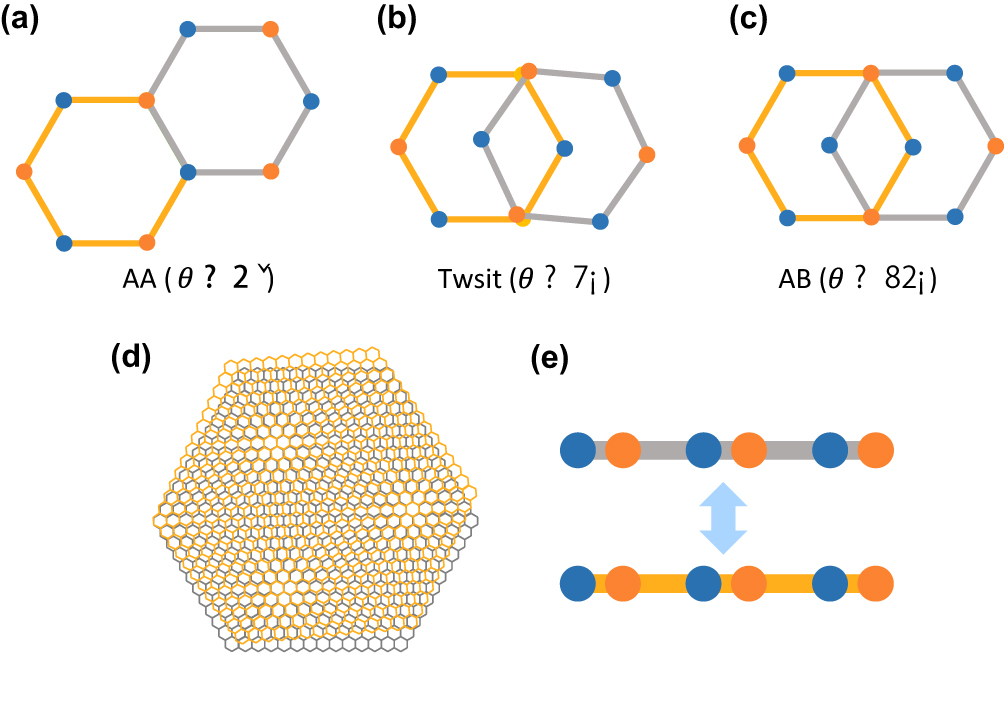
The concept of 2D materials is prevailing accompanied with the discovery of graphene,[1,2] which opens up a new field of material science. 2D materials have many unique physical properties, such as the Dirac cone band structure of monolayer graphene, valley-selective polarized light absorption of transition metal dichalcogenide (TMD), great insulation of hexagonal boron nitride (hBN), and so on.[3–5] Benefitting from the abundance of 2D monolayers, the heterostructures, built by different layer stacking, form a new big family. In sharp contrast to conventional bulk materials, lack of dangling bonds at the surface greatly facilitates the building of heterostructures without further consideration of the lattice mismatch. When one layer is stacked on another forming bilayer, their different lattice vectors can lead to the formation of superlattice, and the electrons in the system will feel an additional potential called moiré periodic potential (Fig.
In this review, we discuss the topic of the 2D twisted bilayer materials, particularly concentrating on how the twist angle determines the physical properties. First, we summarize different methods to fabricate twisted bilayers under different conditions. Then, three typical material systems are discussed: twisted bilayer graphene, graphene/hBN heterostructures, and TMD bilayers. At last, we give our perspectives on the study and applications of 2D twisted bilayer materials.
Fabrication is the first and most fundamental step in material science research. Mainly two challenges exist in the fabrication process of 2D twisted bilayer materials: accurately controlling interfacial twist angle and building clean interface. Generally, if we do not care much about the accuracy of the twist angle, crude methods can satisfy our demands. Common wet transfer or dry transfer method can be used to fabricate twisted bilayer, where polymer is used to pick up one layer from its substrate and stack the layer on another. However, in this way the interface is not clean enough.[12–15] As shown in Fig.
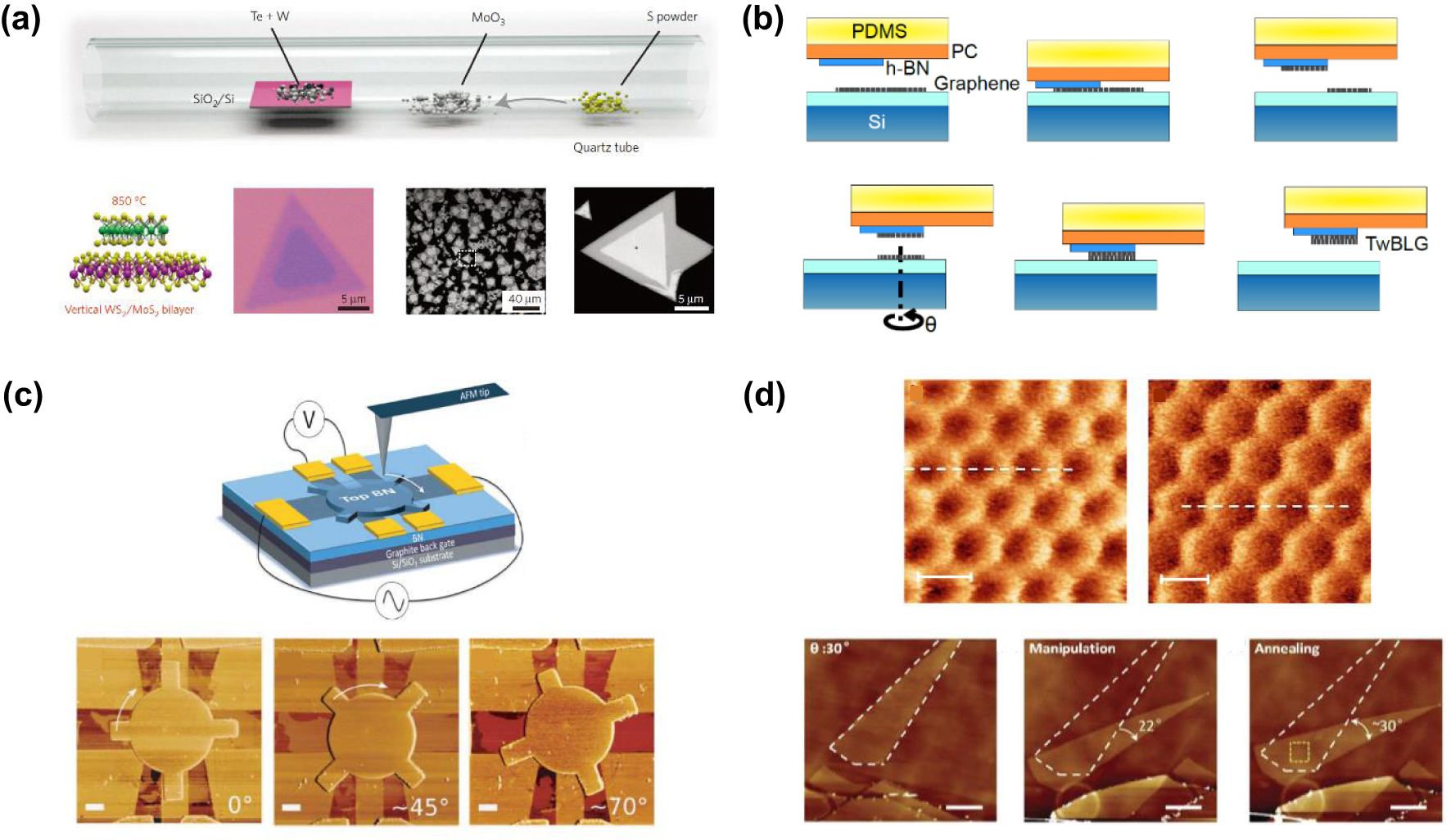 | Fig. 2. Fabrication methods. (a) Top: illustration of CVD growth of vertical WS2/MoS2 bilayers. Bottom: schematic illustration, optical image, and scanning electron microscopy image of vertical WS2/MoS2 bilayers. Reprinted with permission from Ref. [16]. Copyright 2016, Nature Publishing Group. (b) Schematic illustration of ‘tear & stack’ technique, which is essentially a modified dry transfer method to fabricate clean interface with accurate twist angle. Reprinted with permission from Ref. [17]. Copyright 2016, American Physical Society. (c) Schematic illustration and AFM images of the twist-angle-tunable graphene/hBN heterostructures. Reprinted with permission from Ref. [22]. Copyright 2018, American Association for the Advancement of Science. (d) Top: AFM images of graphene/hBN heterostructures before (left) and after (right) annealing. Bottom: AFM images of graphene/hBN heterostructures. They are obtained initially (left), after AFM tip control (middle), and after long-time annealing (right), respectively. Reprinted with permission from Ref. [23]. Copyright 2016, Nature Publishing Group. Reprinted with permission from Ref. [21]. Copyright 2016, American Physical Society. |
In contrast to the methods mentioned above, twisted graphene/hBN heterostructures can be fabricated in other ways as reported, and such methods allow one to regulate the twist angle after fabrication. As shown in Fig.
Monolayer graphene is a 2D Dirac semimetal with many unique properties, such as massless Dirac fermion, high carrier mobility, and wide-spectrum light absorption compared to the conventional materials.[24] As for common intrinsic Bernal stacked bilayer graphene (AB stacking), the bandgap remains zero while the fermion becomes massive.[3] However, when taking the twist angle into consideration, new physical phenomena have been found and investigated in twisted bilayer graphene.
As shown in Fig. 
 |
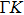
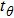
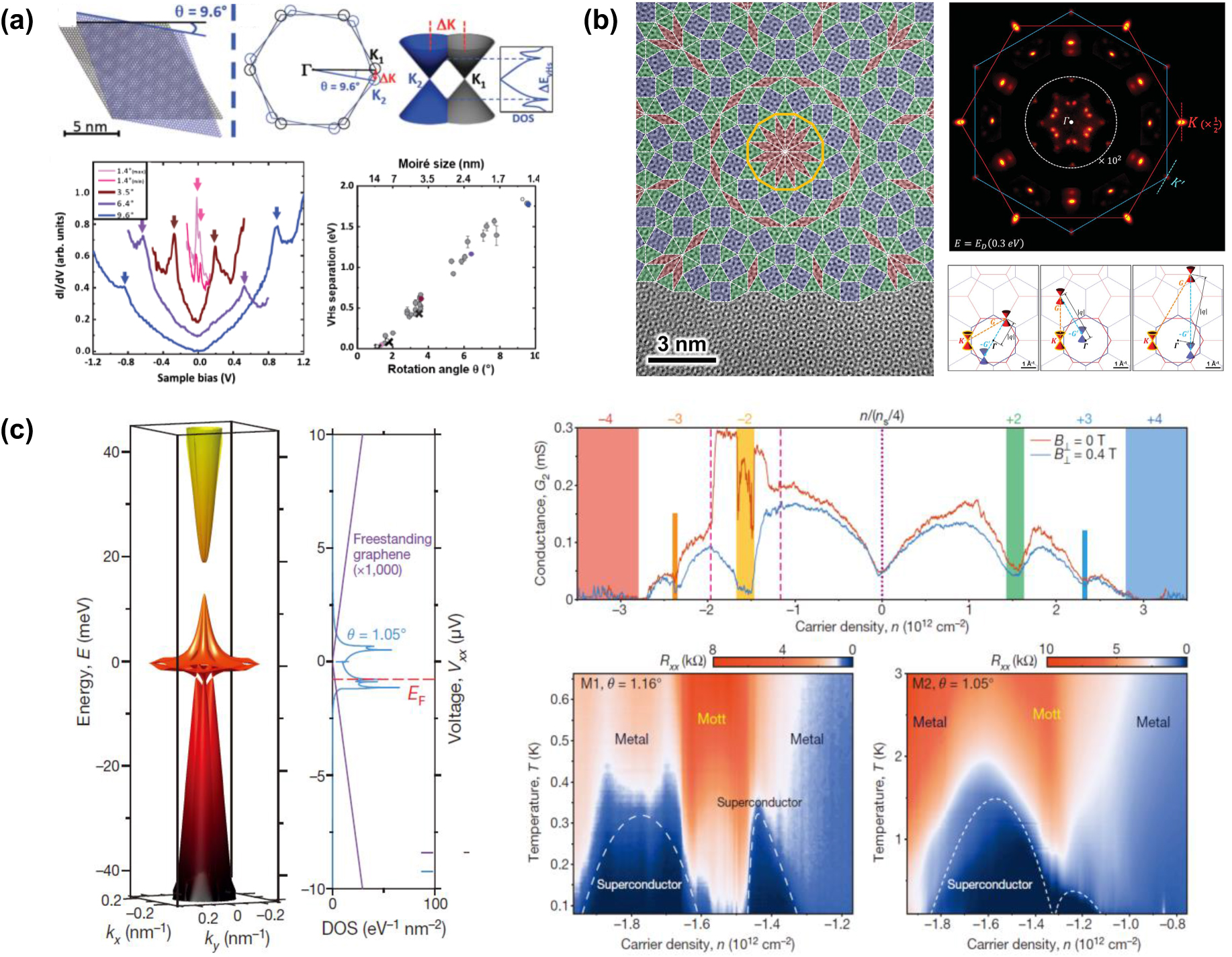 | Fig. 3. Physical properties of twisted bilayer graphene. (a) Schematic illustration and STS results of the new van Hove singularities of twisted bilayer graphene. The interlayer interaction leads to the formation of van Hove singularities, and they correspond to the two peaks in STS measurements. The relation between the singularity energy separation and the twist angle is also shown. Reprinted with permission from Ref. [27]. Copyright 2012, American Physical Society. (b) Left, calculated band structure and density of states of twisted bilayer graphene with twist angle 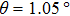

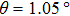
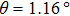
|
In 2010, Morell et al. predicted the occurrence of flat bands (simultaneously, zero Fermi velocity at Dirac point) in twisted bilayer graphene using tight-binding calculations, which probably means the existence of strong electron–electron interaction.[35] In 2011, Bistritzer et al. solved the continuum Dirac model for twisted bilayer graphene and also found a flat band for a series of the so-called magic angles,[18] which was partly (only for the largest twist angle) convinced in 2015 using STS by Yin et al.[36] Later, Cao et al. successfully realized the material system and made various electrical measurements on it.[6,7] At first, they found that the conductance of twisted bilayer graphene becomes zero with the moiré band half-filled and attributed this to the formation of a Mott insulator, which can be explained in rough as the consequence of the split of the moiré band caused by the repulsion of the two electrons in the same orbital state with different spins (Hubbard model).[37,38] Then they made more careful measurements (four-probe resistance 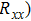
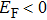
The twist angles mentioned above are mostly small angles. As for large twist angles, the interaction between two layers is usually weak.[49,50] Ahn et al. fabricated twisted bilayer graphene with a twist angle of exactly 30°, which forms a graphene quasicrystal with dodecagonal quasicrystalline order and anomalous interlayer interaction is found by angle-resolved photoemission spectra of the system.[51] Extra scattering points owing to Umklapp scattering process of the two layers are shown in Fig.
In addition to the band structure of electrons, electron–phonon coupling is also a fundamental interaction that affects a broad range of phenomena in condensed matter physics, such as electron mobility, and is responsible for conventional superconductivity.[53] In multilayer structures, the interaction can involve intralayer electron–phonon interaction or interlayer electron–phonon interaction (Figs. 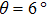
The theoretical results of twisted bilayer graphene mentioned above are all based on a common assumption that the lattice structure of either layer does not change significantly despite the interlayer interaction. However, Yoo et al. reported that this is not the case.[45] In Fig. 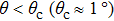
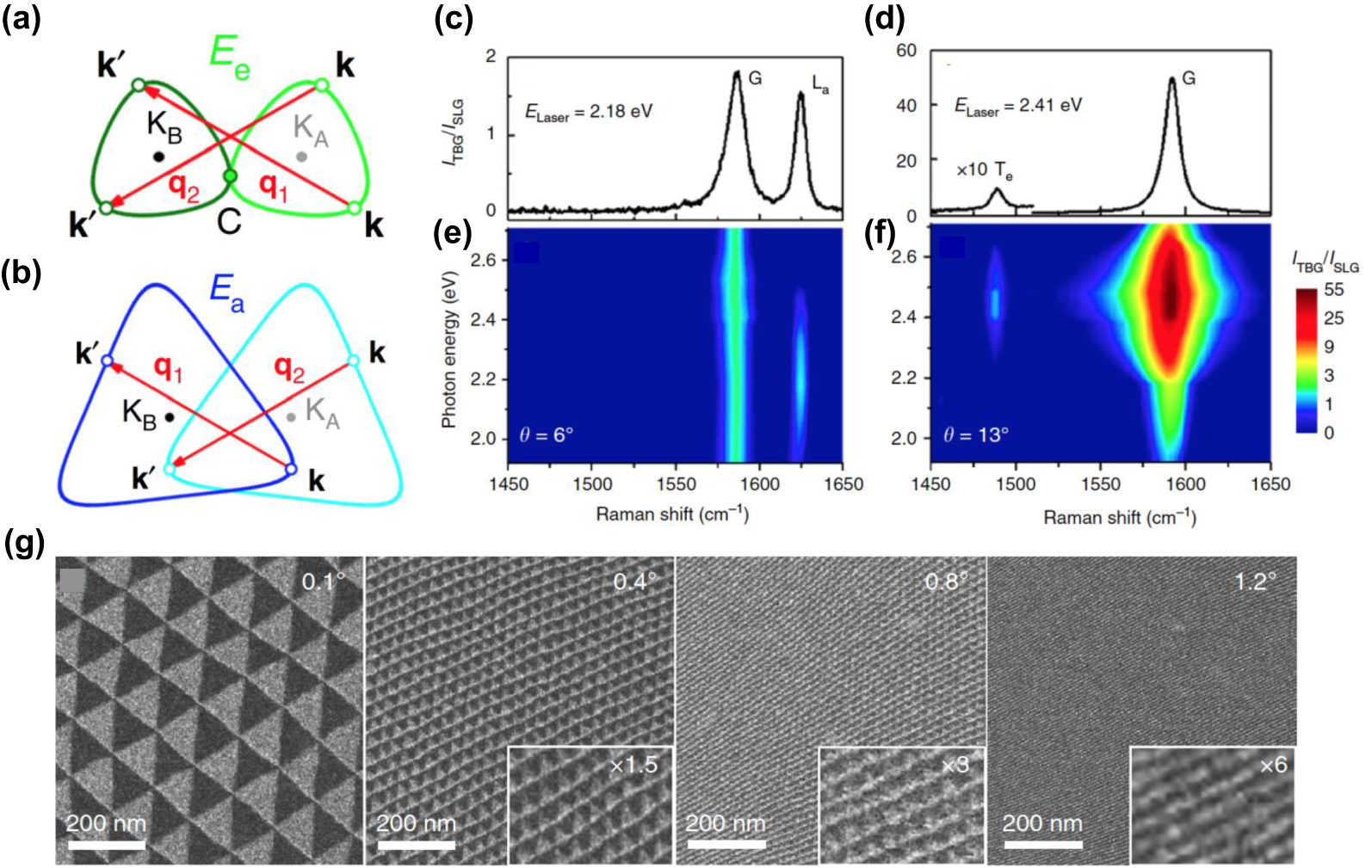 | Fig. 4. Electron–phonon coupling and atomic reconstruction in 2D twisted bilayer materials. (a) and (b) Schematics of interlayer electron–phonon process where a phonon with momentum 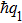

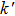
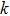

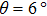
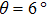
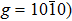
|
The study of graphene/hBN heterostructures became popular after Dean et al. pointed out that hBN can be an appealing substrate for graphene, fairly avoiding various factors which will decrease the quality of graphene in contrast to the standard SiO2 substrate.[64] The experimental results indicate that the coupling between graphene and hBN is generally weak for the band structure of graphene. In 2013, several papers were published discussing the transport properties of graphene/hBN heterostructures, and they particularly concentrated on the so-called Hofstadter butterfly[65] induced by the moiré periodic potential and an external magnetic field, as shown in Fig.
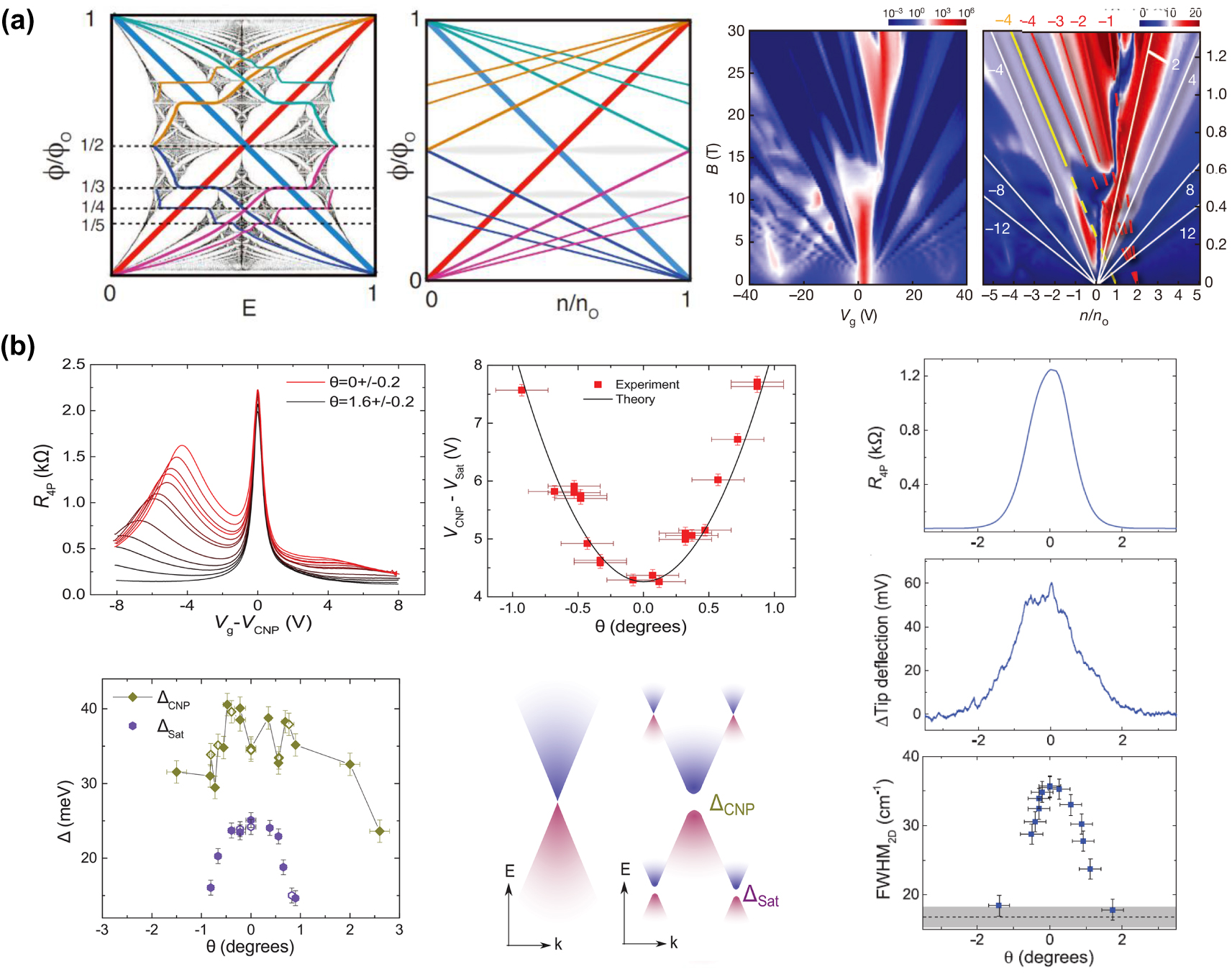 | Fig. 5. Physical properties of graphene/hBN heterostructures. (a) Left, normalized Hofstadter butterfly spectrum for square lattice in a magnetic field. Middle, density-field diagrams of such system. Colored lines stand for constant chemical potential for both two above. Right, transport measurement results of graphene/hBN heterostructures. The slope of each line has been marked in the figure. Reprinted with permission from Ref. [68]. Copyright 2013, Nature Publishing Group. (b) Top left, four-probe resistance as a function of gate voltage (Vg) results. A satellite peak locates away from charge neutrality point and indicates an extra energy gap. Bottom left, energy gap as a function of twist angle. Top middle, satellite peak position as a function of twist angle. Bottom middle, illustration of energy gap. Right, four-probe resistance (R4P), tip deflection (reflection of friction force), and full width at half maximum of the 2D peak (FWHM2D) in Raman spectroscopy as a function of twist angle at a carrier density of 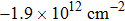
|
After the discovery of graphene, the appearance of TMD materials markedly broadens the 2D materials with diverse physical properties.[73–76] Most TMD materials are semiconductors whose bandgaps cover the range from near-infrared to visible region with strong light–matter interaction, the degenerate exciton transitions at the K and 
Liu et al. investigated photoluminescence and Raman spectra of 44 MoS2 bilayers with different twist angles (Figs. 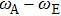
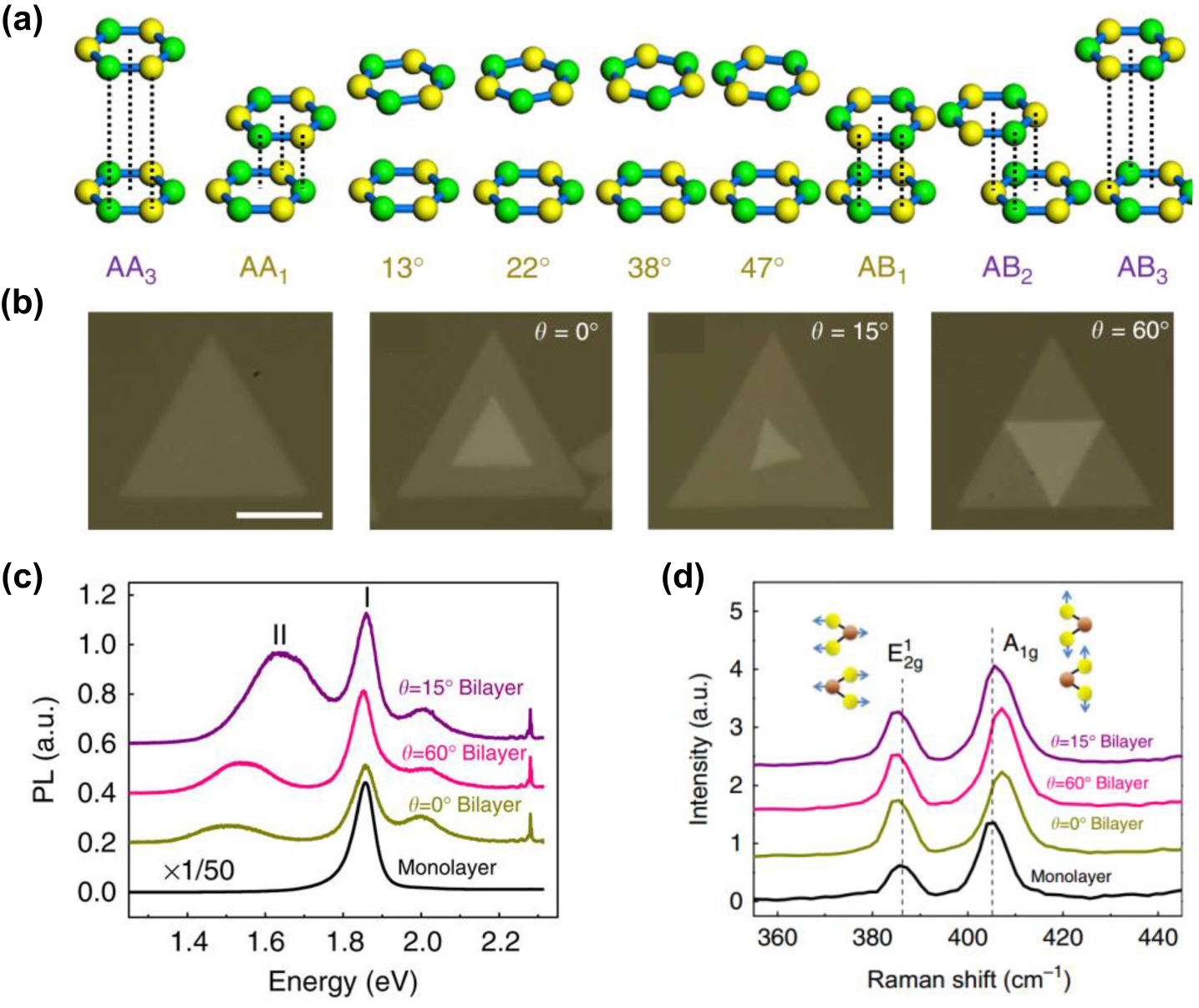 | Fig. 6. Electronic and mechanical coupling in twisted MoS2 bilayer. (a) Schematics of MoS2 bilayers with different stacking configurations. Green spheres are Mo atoms; yellow sphere are S atoms. (a) Optical images of a MoS2 monolayer and twisted bilayers with different twist angles. (c) Photoluminescence and (d) Raman spectra of MoS2 monolayer and bilayers with different twist angles. Reprinted with permission from Ref. [80]. Copyright 2014, Nature Publishing Group. |
TMD heterostructures are of particular interests because many of them form type II heterojunctions, which facilitate the efficient separation of photoexcited electrons and holes and therefore exhibit great potential in the applications of photodetectors, photovoltaics, and sensors. This separation in MoS2/WS2 bilayers could take place within 50 fs upon photoexcitation due to strong interlayer coupling.[84–86] As the interlayer coupling in 2D heterostructure materials varies with interlayer twist angles, Ji et al. have investigated how the interlayer charge transfer in MoS2/WS2 bilayers evolves with different stacking configurations (Fig.
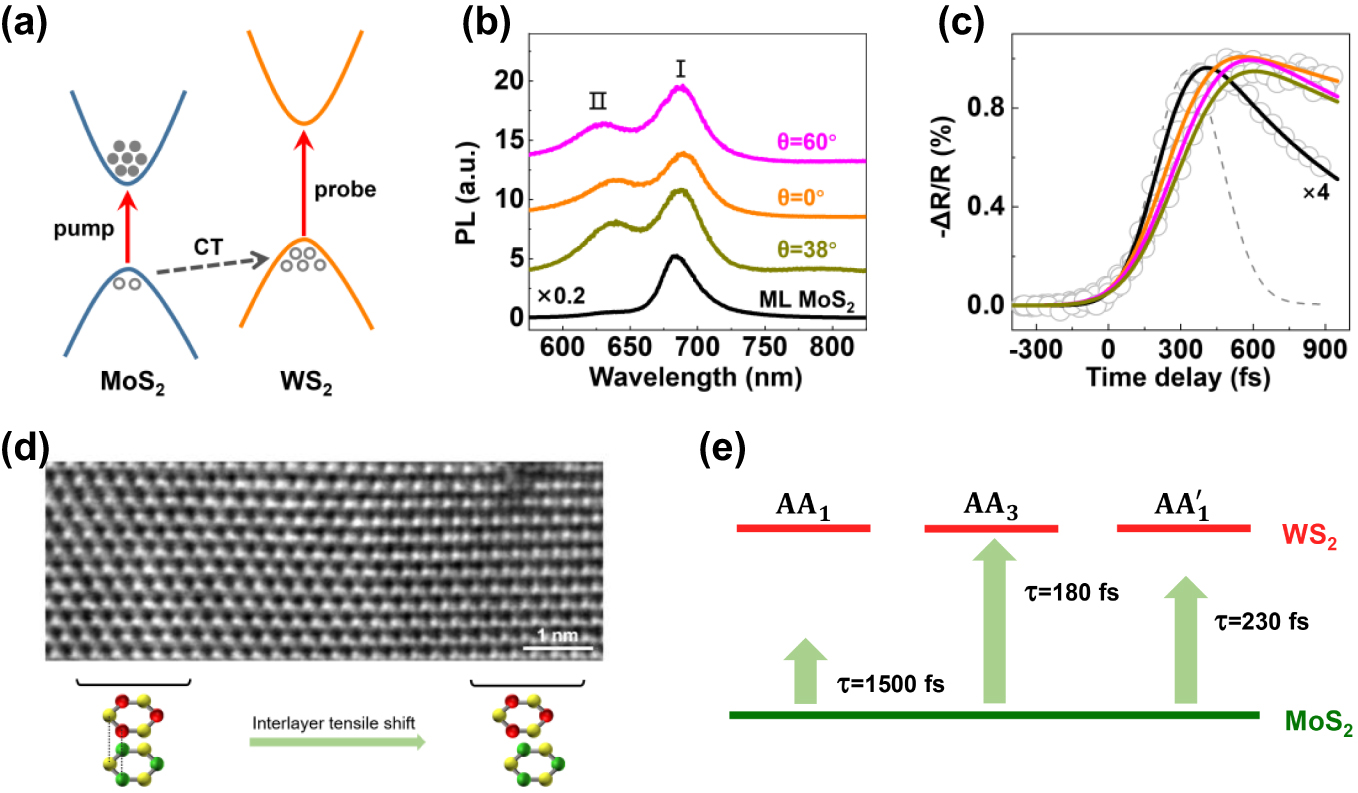 | Fig. 7. Stacking-independent ultrafast charge transfer in TMD heterostructures. (a) Band alignment of MoS2/WS2 bilayers. After pumping MoS2 A-exciton with ultrafast laser, the electron remains in MoS2 while the hole will transfer to a lower energy at WS2, resulting in an efficient electron–hole separation. (b) Photoluminescence spectra of MoS2 monolayer and MoS2/WS2 bilayers. The two obvious peaks in MoS2/WS2 bilayers correspond to direct A-exciton transitions from MoS2 (peak I) and WS2 (peak II), respectively. (c) Transient absorption spectra of MoS2/WS2 bilayers by selectively probing with a higher energy light at WS2 A-exciton resonance. (d) TEM image of an AA stacking MoS2/WS2 bilayer. In addition to the energy-favorable AA1 stacking, there exists high-energy state of AA3 stacking due to interlayer stretching and shifting. (e) Schematic of charge transfer process at the interface of AA stacking MoS2/WS2 bilayers, where multi-channels coexist. The apparent transfer time is mainly determined by the fastest channel. Reprinted with permission from Ref. [87]. Copyright 2017, American Chemical Society. |
In TMD bilayers, there exists a moiré periodic potential as well, so electron–phonon coupling and phonon–phonon interactions can be affected. Lin et al. discovered that the moiré periodic potential in twisted MoS2 bilayer can modify the properties of phonons in its MoS2 monolayer constituent to generate Raman modes related to moiré phonons.[90] They measured the Raman spectra in the region of 50–425 cm−1 of the twisted MoS2 bilayers with twist angles ranging from 9° to 49° under the excitation energy E=2.54 eV. Apart from those modes observed in all twisted MoS2 bilayers independent of θ like longitudinal acoustic (LA) and transverse acoustic (TA) modes, they observed seven series of θ-dependent Raman modes (Figs.
 | Fig. 8. Moiré phonons in twisted MoS2 bilayer. (a) and (b) Raman spectra of twisted MoS2 bilayer in the regions of (a) 50–365 cm−1 and (b) 370–425 cm−1. The Raman modes in different phonon branches are represented by different shapes and color symbols. The Raman spectra of monolayer MoS2 and 3R-bilayer MoS2 (θ =0°) are plotted for comparison. (c) and (d) The comparison of calculated and experimental frequencies of moiré phonons dependent on θ (c) and 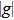
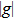
|
Exciton is the particle-like entity that formed by an electron bound to a hole.[91] Moiré excitons are excitons whose energy levels are quantized arising from the lateral confinement imposed by the deep moiré potential.[8,11] Jin et al. reported experimental observation of moiré excitons in WSe2/WS2 bilayers.[8] The optical photograph and schematic diagram are shown in Figs.
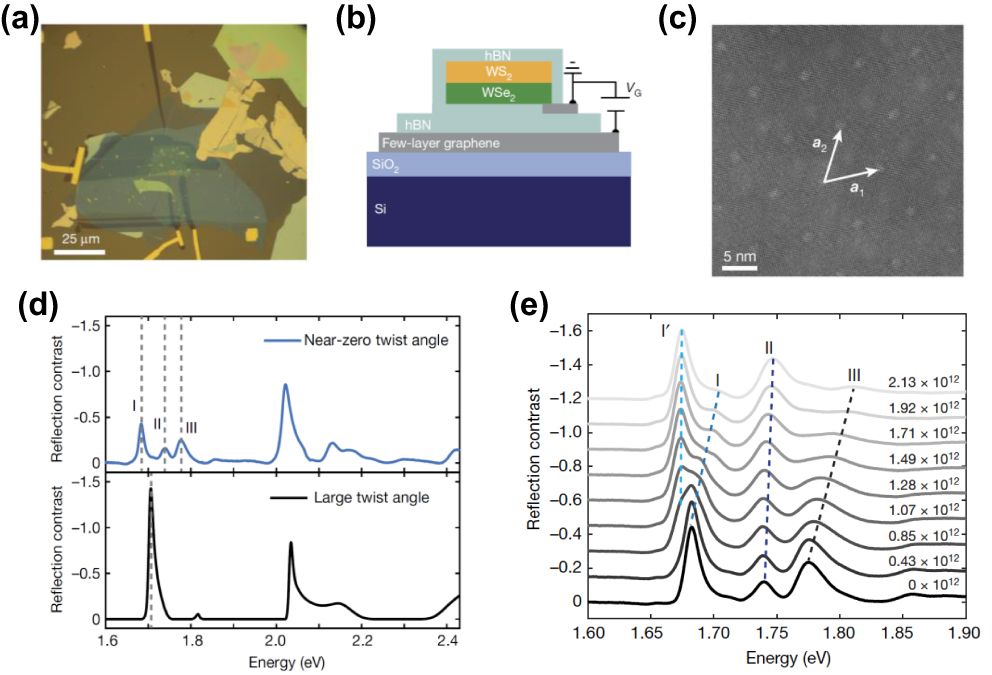 | Fig. 9. Moiré excitons in twisted TMD heterostructures. (a) and (b) Optical microscopy image (a) and side-view illustration (b) of a representative heterostructure with a near-zero twist angle. (c) A zoomed-in image of atomic-resolution STEM of near-zero twist angle WSe2/WS2 bilayers showing the moiré superlattice. The two superlattice vectors are labelled. (d) Reflection contrast spectrum of near-zero twist angle WSe2/WS2 bilayers (top) compared to a large twist angle one (bottom). (e) Reflection contrast spectra in the range between 1.6 eV and 1.8 eV of the WSe2. A exciton upon electron doping. The electron concentration is noted for each spectrum in units of cm−2. Reprinted with permission from Ref. [8]. Copyright 2019, Nature Publishing Group. |
As introduced above, engineering physical properties of 2D bilayers by interfacial twist angle has become a hot topic in recent years. This is mainly achieved by two mechanisms, tuning interlayer coupling and moiré periodic potential by tuning the twist angle. Although various novel physics have been found in the 2D heterostructure family, many of them such as the unconventional superconductivity and stacking-independent ultrafast interfacial charge transfer still demand deeper understanding. Also, developing a universal approach to continuously tuning the twist angle and thereby modulating their physical properties is required. At last, massive production of clean interface with accurate twist angle and large-area single crystal is the main challenge for the real applications based on 2D heterostructure family, which should be on the schedule to be explored.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 | |
| 62 | |
| 63 | |
| 64 | |
| 65 | |
| 66 | |
| 67 | |
| 68 | |
| 69 | |
| 70 | |
| 71 | |
| 72 | |
| 73 | |
| 74 | |
| 75 | |
| 76 | |
| 77 | |
| 78 | |
| 79 | |
| 80 | |
| 81 | |
| 82 | |
| 83 | |
| 84 | |
| 85 | |
| 86 | |
| 87 | |
| 88 | |
| 89 | |
| 90 | |
| 91 |