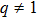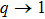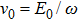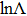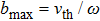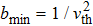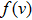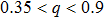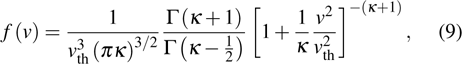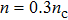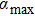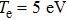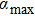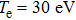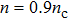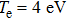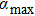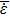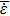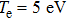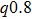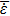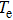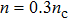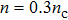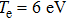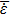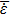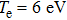The inverse Bremsstrahlung absorption in the presence of Maxwellian and non-Maxwellian electrons
Physics Department, Yazd University, Safaeyeh, Yazd, P. O. Box 891995-741, Iran
† Corresponding author. E-mail:
mehdi.sharifian@yazd.ac.ir
1. IntroductionAs we know, laser–plasmas interaction is one of the contemporary problems and has applications from plasmas diagnostics and x-ray radiation generation to fusion.[1] The most important absorption mechanism in laser–plasmas interactions is collisional absorption by the inverse Bremsstrahlung (IBA) process. The collisional absorption, or IBA, is the radiation absorbed by electrons when they scatter in the Coulomb field of ions.[2]
Re-discovering of this absorption mechanism is required to check the electrons distribution function which plays the main role in this mechanism. Maxwellian distribution function has been usually assumed in many works related to the laser–plasmas interactions.[3,4] This distribution is valid only for systems in thermodynamic equilibrium. Sometimes it could be found that the ions distribution function is Maxwellian but the electrons are generally in near-thermal equilibrium.[5]
However, through observation (i.e., the experimental data), it emerges that space plasma is far away from its equilibrium state.[6,7] Non-Maxwellian electrons could cause plasma to deviate from thermodynamic equilibrium.[8] In a fusion system, the electrons distribution is not perfectly Maxwellian, therefore the system which will be considered in this work is of interest because it deviates from the equilibrium state. For the exact discussion of IBA especially in plasma fusion, a non-Maxwellian distributions such as q-nonextensive distribution and Kappa distribution functions that would be observed in this kind of plasmas will be considered here.[9]
In recent years, great attention has been paid to the use of non-extensive statistic mechanics or Tsallis statistics in cases that Maxwellian function is inapplicable, e.g., in long-range interactions and correlations.[7,10] Renyi acknowledged the non-extensive generalization of the Boltzmann–Gibs–Schannon (BGS) entropy for statistical equilibrium in 1955.[11] Then, it was investigated and proposed by Tsallis in 1988.[12] This distribution is explained by a non-extensive parameter (q) that relates the basic dynamics of the plasmas system and measures the quantity of its non-extensivity.[13] The q-nonextensive distribution describes power-law distribution functions for
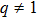, and it gives a Maxwellian distribution function when
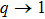.[7,14]
If the plasmas electrons distribution function has a super-thermal power-law tail with high energies, it is better to use Kappa distribution instead of Maxwellian distribution function for electron.[9] The Kappa distribution function at high velocities obeys an inverse power, and, when
, it approximates the Maxwellian distribution.[15] Generally, this function gets both in and out of thermodynamic equilibrium.
Another issue in the laser–plasmas interaction is the average energy absorption rate per unit volume,
. The average energy absorption is the conversion of energy between the oscillating electric field of laser and plasmas (matter), which strongly depends on the electrons distribution function.[16]
For better understanding of absorption, it is better to study the fractional absorption and the averaged energy absorption by using non-Maxwellian distribution functions. In this paper, we deal with the fractional absorption (α) and the average energy absorption (
) using the kinetic theory and the ballistic model (BM), proposed by Mulser et al.[4] for several distribution functions including Maxwellian, q-nonextensive, and Kappa distribution functions.
The paper is organized as follows. In Section 2, the equations of absorption and average energy absorption are presented. Then, the equations of distribution functions are given too. By applying these distribution functions, the results are used to investigate the absorption and the average energy absorption in Section 3. Finally, Section 4 is devoted to the summary and conclusion.
2. The basic equationWe assume an under-dense plasmas in the presence of a laser electric field, E, at the wavelength of λ = 800 nm(resonance absorption does not occur at this wave length[3]). The evolution of the fractional absorption in the plasmas space is given by[17]
where
L is the plasmas length which t is assumed to be 5
λ, and
ki can be written as
where
c is the light velocity,
is the average collision frequency, and
n and
nc are the plasmas density and the critical plasma density, respectively. They are assumed as
, unless mentioned. We use the ballistic model for
, which is given as
[4]where
as the oscillatory velocity of an electron during one laser period is
, and the initial velocity of an electron
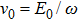
, with
E0 and
ω being the strength of the electric field and the laser field frequency. There is also
(in this study, atomic units (a.u.) have been used), in which
Z = 1,
(
is the plasma frequency), and
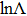
as the Coulomb logarithm is given by
. The equations
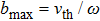
and
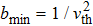
refer to the large impact parameter and the small impact parameter, respectively. Moreover,
vth is the electron thermal velocity, and
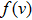
is the electron velocity distribution function. Here, we have used the following three distribution functions. The three-dimensional Maxwellian distribution function is given by
Conventionally, the three-dimensional
q-nonextensive distribution function is given by
[18]where the normalization constant characteristics are
Here
m is the electron mass, and
kB is the Boltzmann constant. Also,
q denotes the non-extensivity degree of the system whose acceptable limit for the absorption is
.
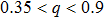
For considering the absorption by using the q-nonextensive function, we substitute Eq. (5) into Eq. (1) and use Eq. (3) to obtain
At last, the three-dimensional Kappa distribution function is given by
[9,19]where Γ is the gamma function, and
κ is the spectral index. The Kappa distribution is equivalent to the
q-nonextensive one under the transformation between the
q characteristic and the
κ index.
[6]The equation for the averaged energy absorption rate per unit volume is written as[20]
This energy absorption is related to the distribution function. The next section of this paper presents an investigation of the fractional absorption and the averaged energy absorption rate per unit volume using the Maxwellian distribution function, the
q-nonextensive distribution function, and the Kappa distribution function.
3. Results and discussionWe have studied the fractional absorption (α) and the average energy absorption (
) for unmagnetized and homogeneous plasmas. In subSection 3.1, using the q-nonextensive distribution function, we have calculated the effects of laser intensity, temperature, and density on α and
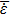. Then, in subSection 3.2, by the use of the same function, these effects have been compared with respect to the results of Maxwellian distribution and Kappa distribution functions.
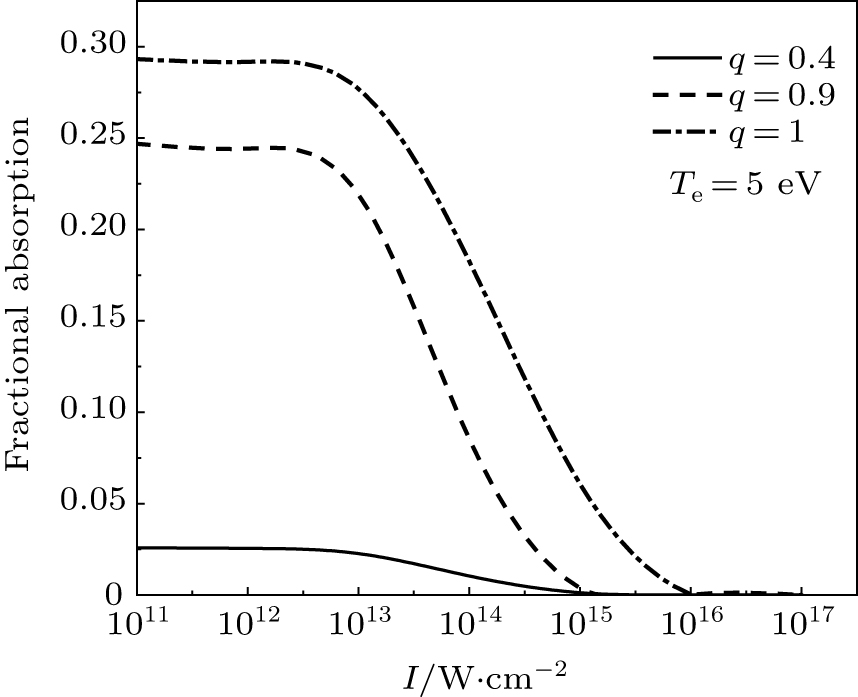
3.1. The study of absorption using the q-nonextensive distribution functionIn this subsection, by using Eq. (8), we investigate the effective parameters on the absorption. One of these parameters is the intensity. Figure 1 shows the absorption coefficient of various q characteristics vs. the intensity of laser in the q-nonextensive distribution for
and
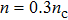. According to this figure, at low intensities, namely, 1011–1013 W/cm2, the variation of the absorption function is fixed with respect to the laser intensity (it is noted that the highest rates of absorption occur within the range of this intensity). Then, above the intensity of 1013 W/cm2, the absorption falls. Finally, for intensities higher than 1015 W/cm2, there occurs no absorption. The maximum rate of absorption (
) is about 30% for q = 1 (i.e., the Maxwellian function). At q = 0.35, where the minimum acceptable characteristic exists, the maximum absorption is about 2% in the intensity range of 1011–1013 W/cm2.
The
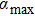in the q-nonextensive distribution is 25% at the intensity of 1012 W/cm2 that occurs at
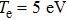, and the minimum value of absorption (
) is 10% at
(see Fig. 2). Figure 2 displays the dependence of the fractional absorption on the laser intensity at various temperatures (this figure is plotted for q = 0.9 at temperatures 5 eV, 10 eV, and 30 eV). As it can be seen,
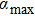is 25% at the intensity of 1011 W/cm2 that occurs at
, and the minimum value (
) of absorption is 10% at
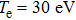. The absorption decreases at low temperatures, for example, at 5 eV and 10 eV, and at intensities higher than 1013 W/cm2. However, for high temperatures, such as 30 eV, it drops at intensities higher than 1014 W/cm2. Also, it is zero at the temperature of 30 eV at high intensities, as compared to other temperatures.
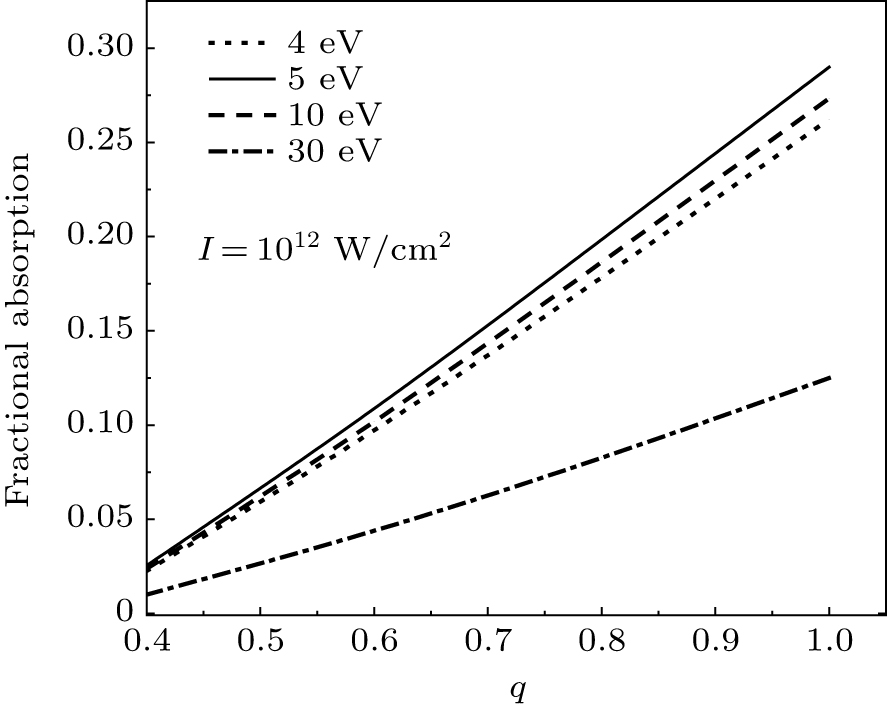
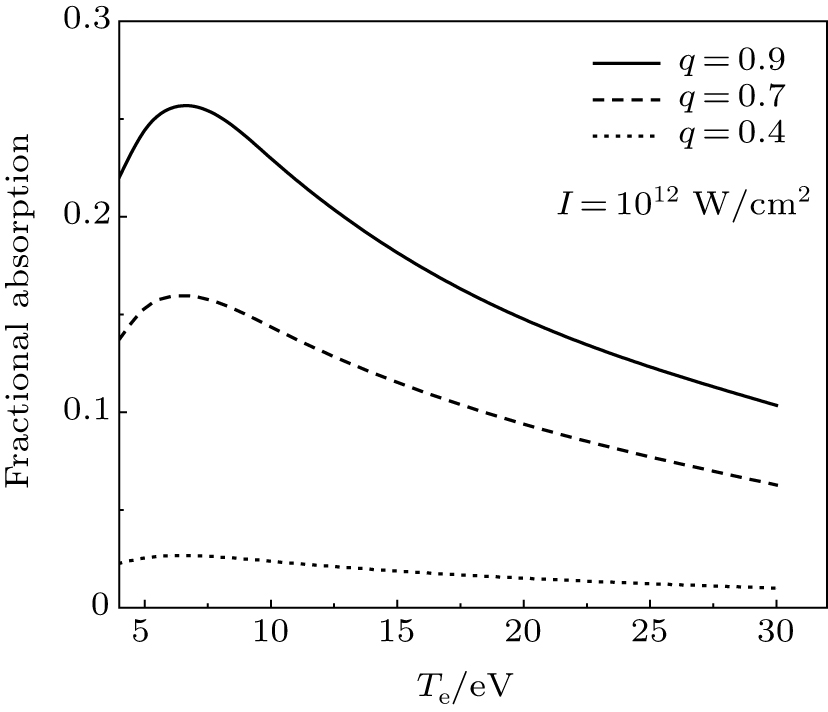
Variations of the q characteristic change the absorption. Figure 3 depicts the absorption as a function of the q characteristic at 1012 W/cm2 for
, 5 eV, 10 eV, and 30 eV. According to Fig. 3, firstly, with a rise in the value of q, the fractional absorption rises too. Secondly, at a low temperature, namely, lower than 5 eV, with an increase in the temperature, the fractional absorption increases too. Above the temperature of 5 eV, the absorption decreases until
is 30 eV. Here, the absorption is at its lowest value.
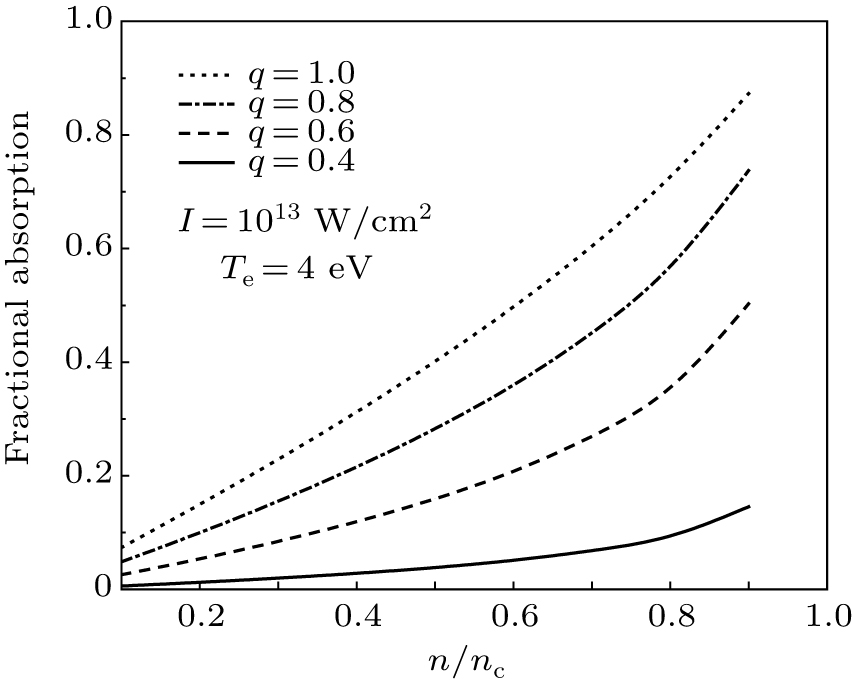
Figure 4 indicates the absorption for the q-nonextensive function in diverse densities, for q = 0.4, 0.6, 0.8, and 1 at
of 4 eV and the intensity of 1013 W/cm2. When the plasma density increases, the absorption increases too;
is about 90% at
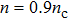for q = 1 (Maxwellian function). The absorption increases nonlinearly when q rises.
Our results show that for all of the q values,
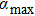occurs at I = 1012 W/cm2. For example, for q = 0.8, the rate of the fractional absorption is 20%. Figure 5 is provided to study the absorption with respect to q for various intensities at
. It can be deduced that the increase of the absorption is linear with the growth of q at intensities of 1012–1013 W/cm2, but for the other intensities, namely, 1014–1015 W/cm2, this increase is nonlinear. At the intensity of 1015 W/cm2, with an increase in q, the absorption does not change much and is almost 5% for q = 1. Whereas the maximum absorption occurs at I = 1012 W/cm2, we study the variation of the absorption with the temperature at this laser intensity. Figure 6 shows the absorption variation for q=0.4, 0.7, and 0.9. As it can be seen,
occurs at Te of 6 eV, and the absorption for q=0.9 and 0.7 is almost 25% and 16%, respectively. The absorption has a direct relationship with the temperature up to
. Above this temperature, however, the absorption begins to decrease.
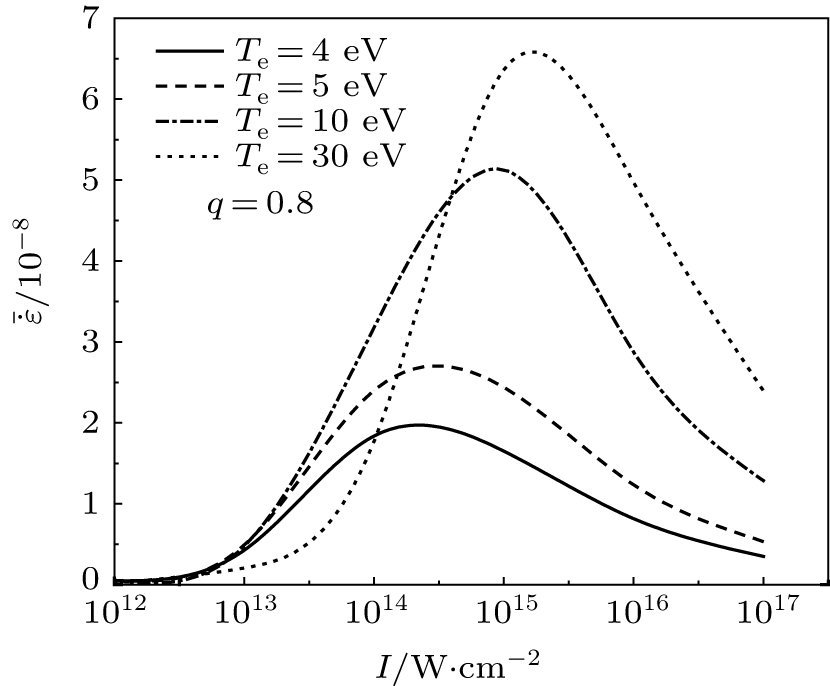
The average energy absorption depends to the distribution function. The results based on the q-nonextensive distribution are plotted in Figs. 7 and 8. Figure 7 depicts the variation of the average energy absorption (
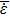) with respect to the laser intensity when q = 0.8 at various temperatures. According to Fig. 7, if the temperature rises, the average energy absorption increases, and the peak of the graphs moves to high intensities.
In Fig. 8,
versus the laser intensity is shown at the
of 4 eV for several q values. As observed,
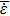has the maximum value for the Maxwellian function (here, q is 1 for the q-nonextensive distribution), and the average energy absorption decreases with a decrease in the q characteristic. At q = 0.4,
has the minimum value. This peak in the graphs is created at intensities about 1014–1015 W/cm2. When the electron temperature is increased, the peaks advance to higher intensities.
3.2. Comparison of absorption using the three distribution functionsNow, we consider the absorption based on distribution functions (4), (5), and (9). In Fig. 9, the fractional absorption is illustrated as a function of the laser intensity at
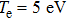and
. Figure 9 is provided to study and compare the absorption rates using the Maxwellian distribution, the Kappa distribution, and the q-nonextensive functions. The absorption based on the Kappa distribution is close to that based on the Maxwellian function at all intensities. Whenever the κ index increases, the absorption moves close to the Maxwellian function. When
, the Kappa distribution is equal to the Maxwellian function. This result is true for low intensities, but, at high intensities, this function coincides with the q-nonextensive function. As it can be seen in Fig. 9, the q-nonextensive function has the lowest absorption at all intensities except at intensities higher than 1014 W/cm2 where it equals the Kappa distribution function at κ = 10.
For all of the distribution functions,
occurs at Te of 6 eV. Figure 10 shows the absorption as a function of temperature for the Maxwellian distribution, the Kappa distribution (with κ = 10), and the q-nonextensive distribution (with q = 0.9) at the same intensity (I = 1012 W/cm2). The rate of absorption is almost 30%, 28%, and 25% for the three distribution functions, respectively. The absorption increases as the temperature rises to 6 eV. Above this temperature, the absorption decreases as the temperature increases.
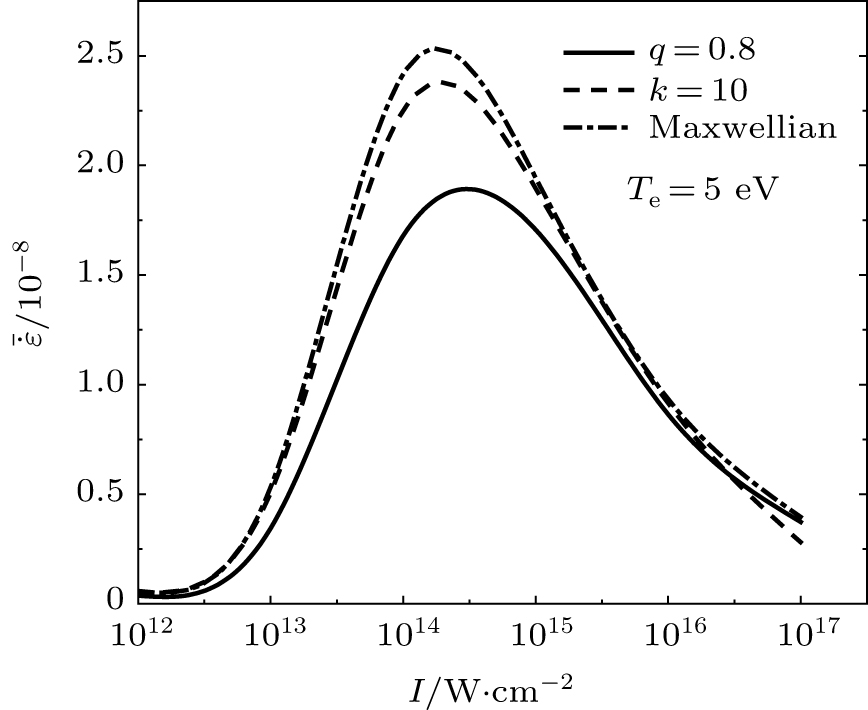
Figure 11 presents the relationship of the average energy absorption and the laser intensity at the same temperature (5 eV) for all the three distribution functions. As it can be seen, the lowest
is obtained for the q-nonextensive distribution with
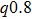. For q = 1 (where the q-nonextensive function is identical to the Maxwellian function),
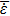is at its maximum. The average energy absorption belonging to the Kappa distribution is closer to that of the Maxwellian function than the q-nonextensive distribution. The peaks of these graphs are set at the intensities of about 1014–1015 W/cm2. Once the electron temperature rises, these peaks advance to higher intensities. For example, at the Te of 30 eV, the peaks of the graphs lie at the intensities of about 1015–1016 W/cm2.
4. Summary and discussionIn this study, the kinetic theory and the BM model were investigated for the average energy absorption using various distribution functions. The results showed that, when the q-nonextensive distribution is used, α is independent of the laser intensity at low values, but the fractional absorption decreases at high laser intensities. Also, the absorption is increased as the q parameter rises and the temperature decreases at different laser intensities. However, at the intensity of 1013 W/cm2, the absorption keeps the same at the temperature of 4–5 eV as the q parameter is increased. Regarding α as a function of the plasma density, it increases nonlinearly. Also,
, as a function of the laser intensity, has its maximum for the average energy absorption at various temperatures. As it was observed, when the temperature and the q characteristic increase, the average energy absorption increases too. In this study, we investigated and compared the absorption using the Maxwellian distribution, Kappa distribution, and q-nonextensive distribution functions. The absorption rate for the Kappa distribution is closer to that for the Maxwellian function than the q-nonextensive distribution at all intensities. The absorption at
for the Kappa distribution and at q = 1 for the q-nonextensive function is equal to that for the Maxwellian distribution function. Also
occurs at the
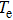of 6 eV for all the three distribution functions. The rate of the average energy absorption for the Kappa distribution is closer to that for the Maxwellian function than the q-nonextensive distribution. The graph peaks of the average energy absorption proved to appear at the intensities of about 1014–1015 W/cm2, and by a rise in the temperature, they would move to higher intensities.
