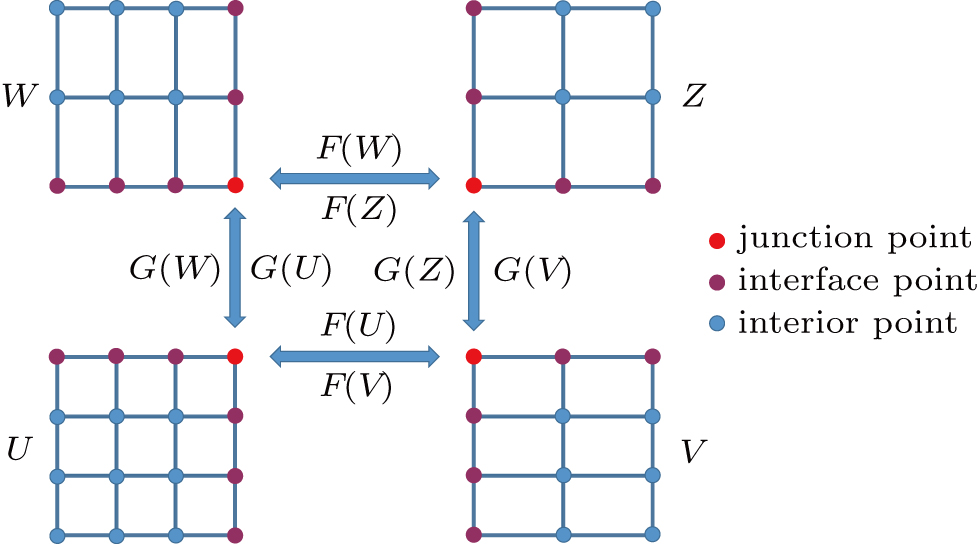
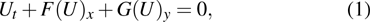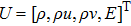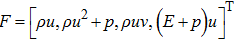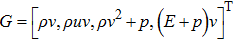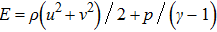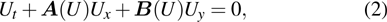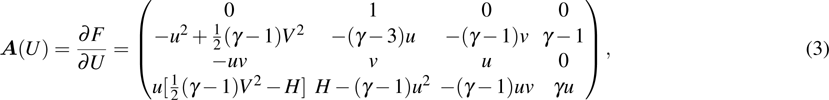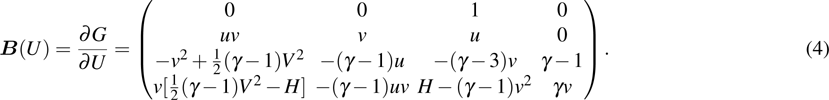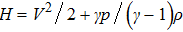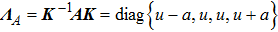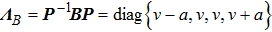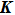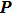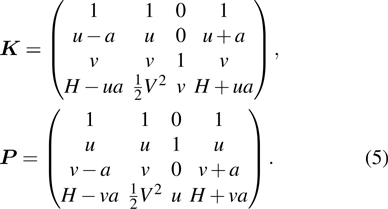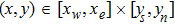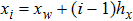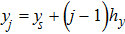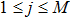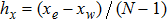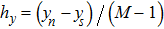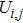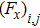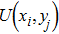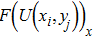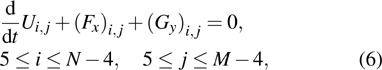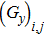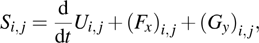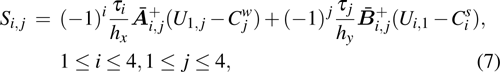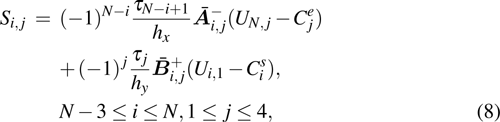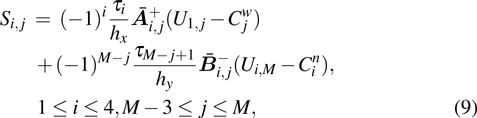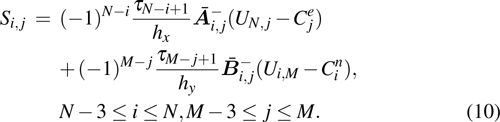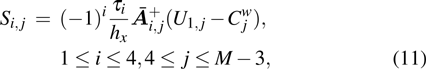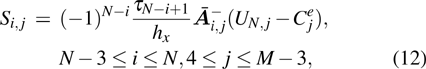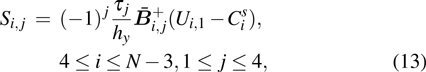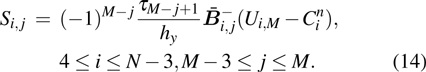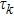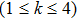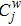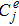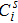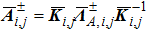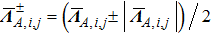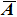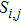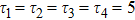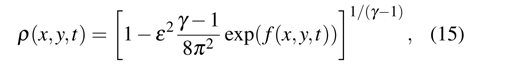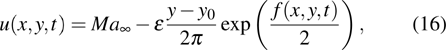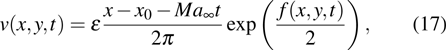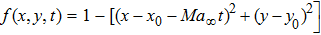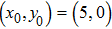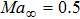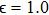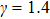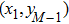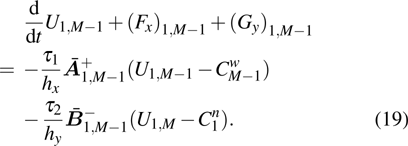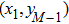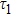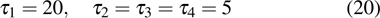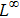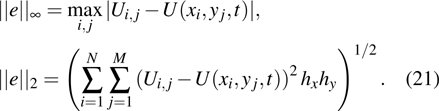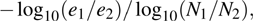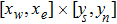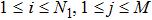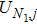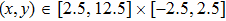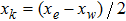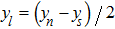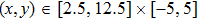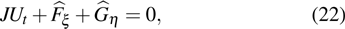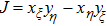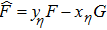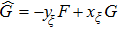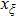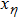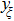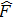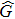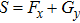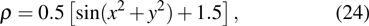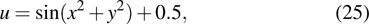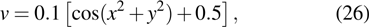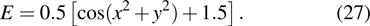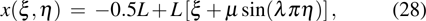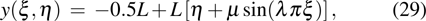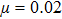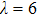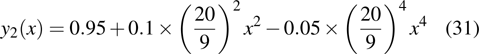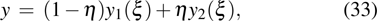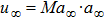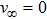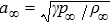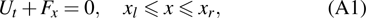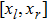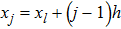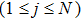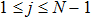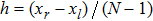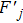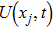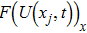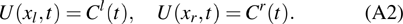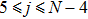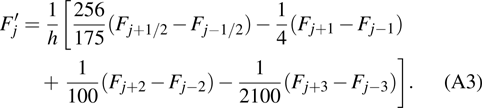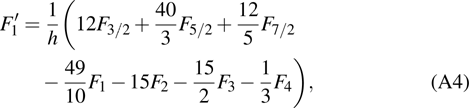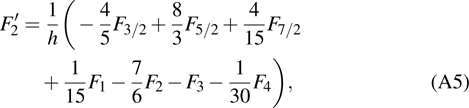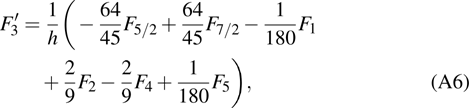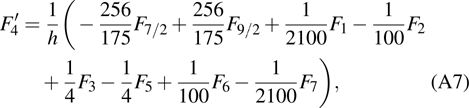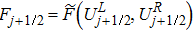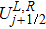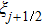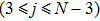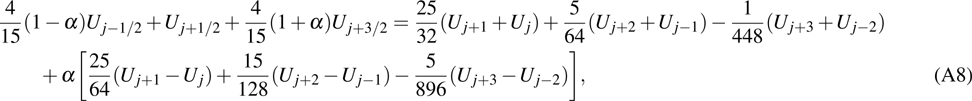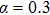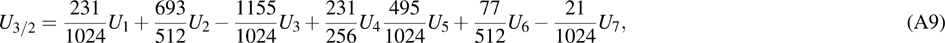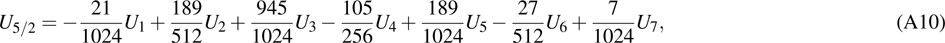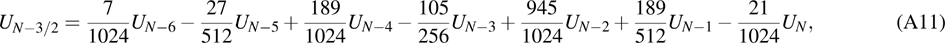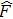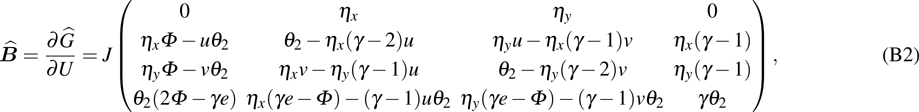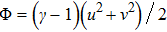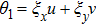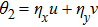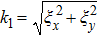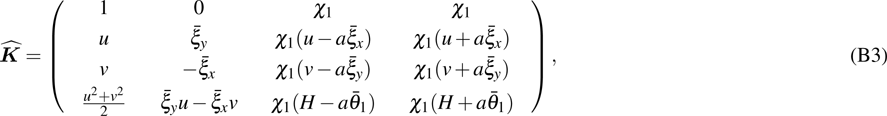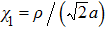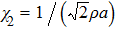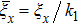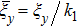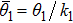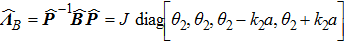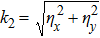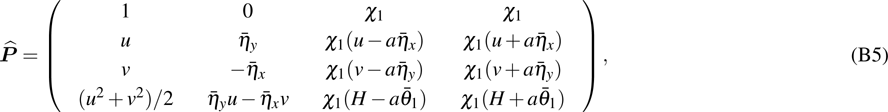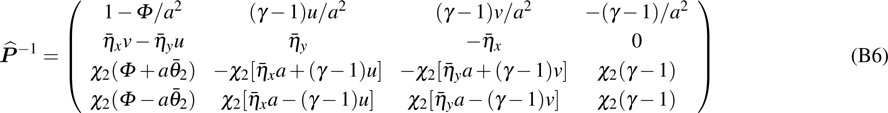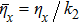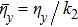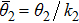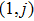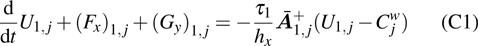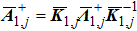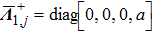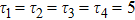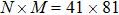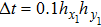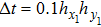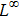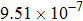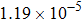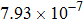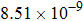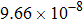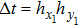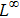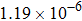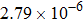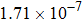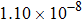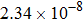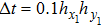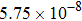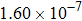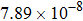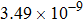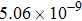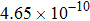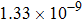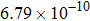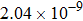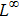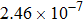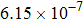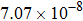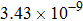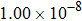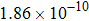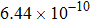are the fluxes in different directions. Here the total energy is set to be
for air.
2.1. Numerical schemeTo extend the seventh-order scheme considered in Ref.[6] (some details can also be found in Appendix A) to solve Eq. (1), it necessitates to consider its quasi-linear form[18]
where the Jacobian matrices
Here
 , and
, and
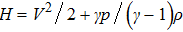 is the specific enthalpy. In addition, the Jacobian matrices can be diagonalized as
is the specific enthalpy. In addition, the Jacobian matrices can be diagonalized as
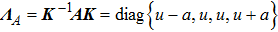 and
and
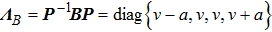 , where
, where
 represents the sound speed,
represents the sound speed,
 and
and
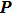 read explicitly as
read explicitly as
For a computational domain
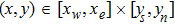 , we denote the discrete coordinates by
, we denote the discrete coordinates by
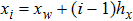 with
with
 and
and
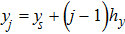 with
with
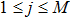 , where
, where
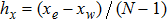 and
and
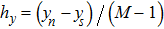 are the spacial steps in different directions. Let
are the spacial steps in different directions. Let
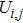 and
and
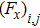 be the approximations to
be the approximations to
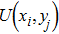 and
and
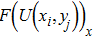 , respectively, and similar notations for other fluxes and matrices. Then the interior semi-discrete scheme for Eq. (1) can be written as
, respectively, and similar notations for other fluxes and matrices. Then the interior semi-discrete scheme for Eq. (1) can be written as
where the expressions for

and
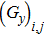
are presented in Appendix A (see also Ref.
[6]). For other points near boundaries, boundary values are involved, which are imposed weakly by using SATs. By introducing the notation
the approximations at the four corner regions read
For other points, the following semi-discrete approximations are used:
Here
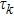
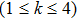
are penalty coefficients that can be tuned to stabilize the scheme,
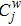
,
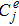
,
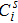
, and

stand for the well-posed west, east, south, and north boundary conditions, respectively. In addition,
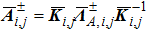
with
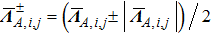
, where the notation
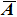
represents the frozen value of

at the last time step. Similar notations also apply for

. It is observed that the added SATs
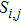
in Eqs. (
7)–(
14) vanish when the exact solution is switched into the scheme, meaning that the implementation of SAT method does not contribute to the truncation error and thus does not affect the convergence rate of the original scheme.
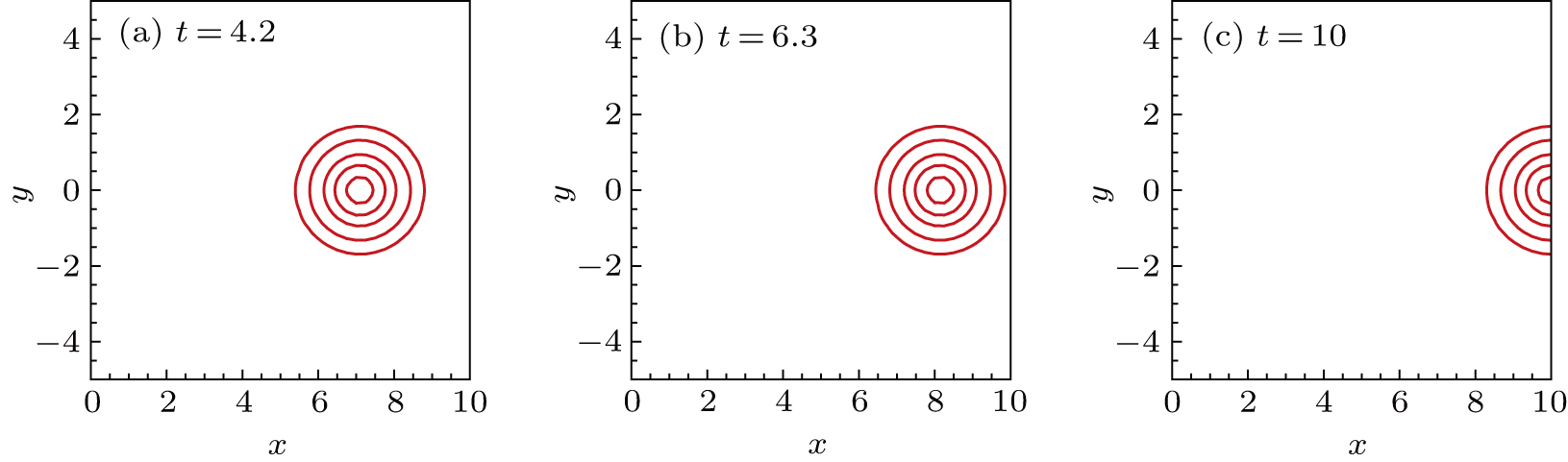
Intuitively, one may simply choose the penalty coefficients to be same values as the one-dimensional case, i.e.,
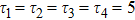 .[6] To test this choice, we take as an example the vortex model from Ref.[19], whose solution is given by
.[6] To test this choice, we take as an example the vortex model from Ref.[19], whose solution is given by
where
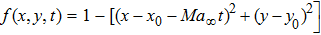
. Here the parameters
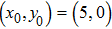
,
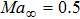
,
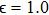
, and
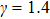
are used. The computational domain is set to be
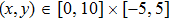
and the time step
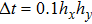
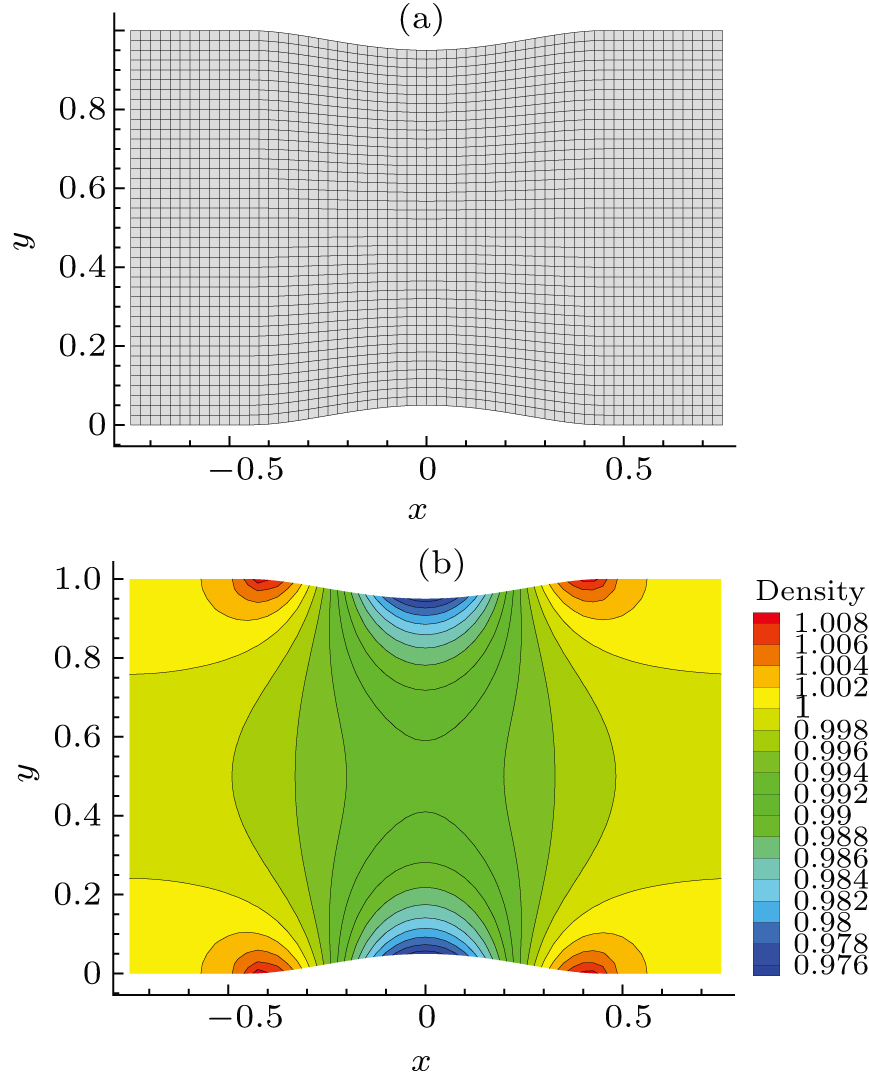
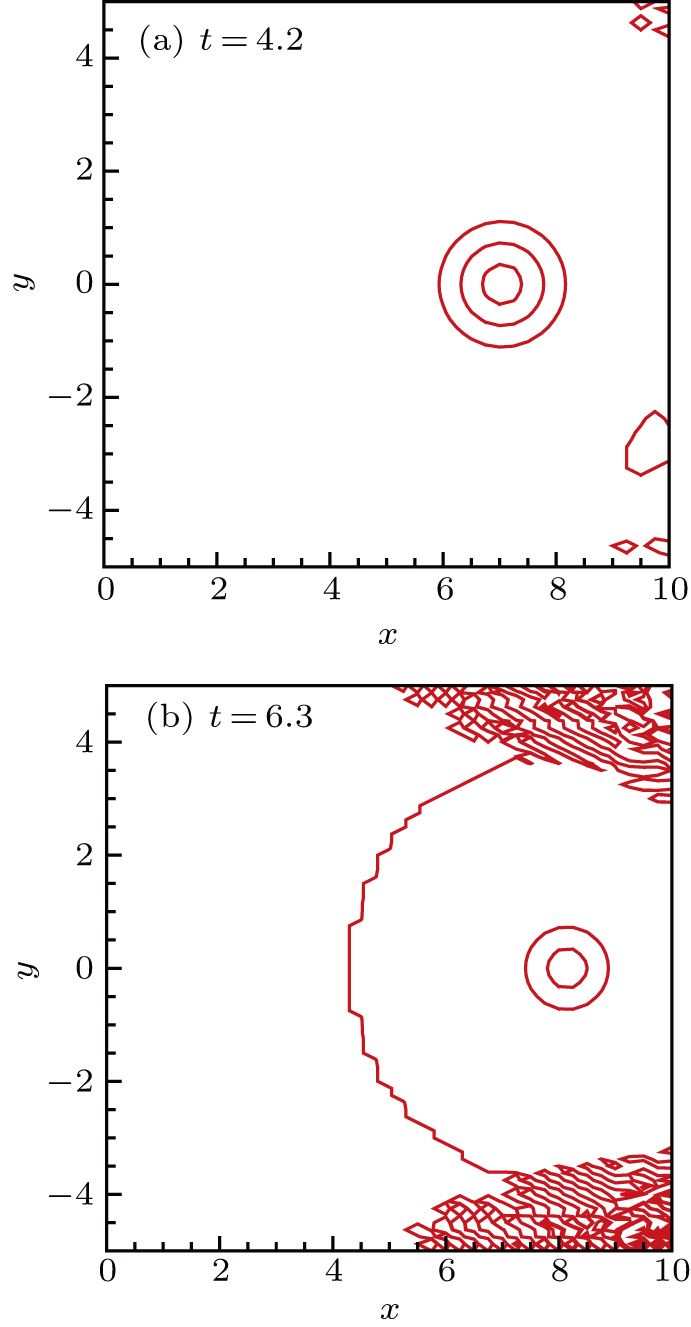
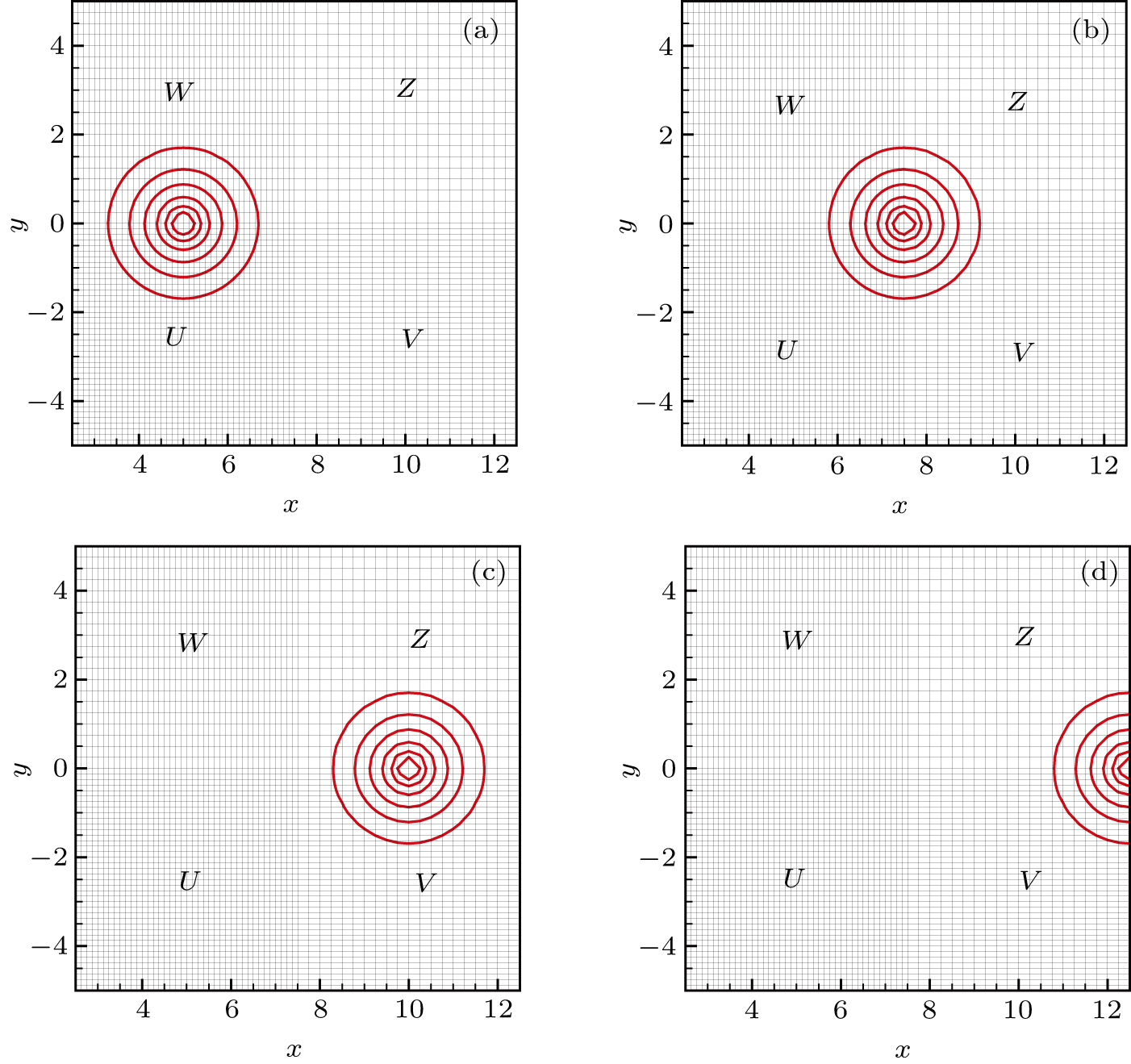
is chosen to implement a traditional fourth-order Runge–Kutta scheme. If not stated otherwise, this time scheme will be used for other numerical examples presented in this paper. For simplicity, exact solution values are adopted at the boundaries. One can observe from Fig.
1 that at
t=4.2 the density solution near the right corners starts to deteriorate, while at
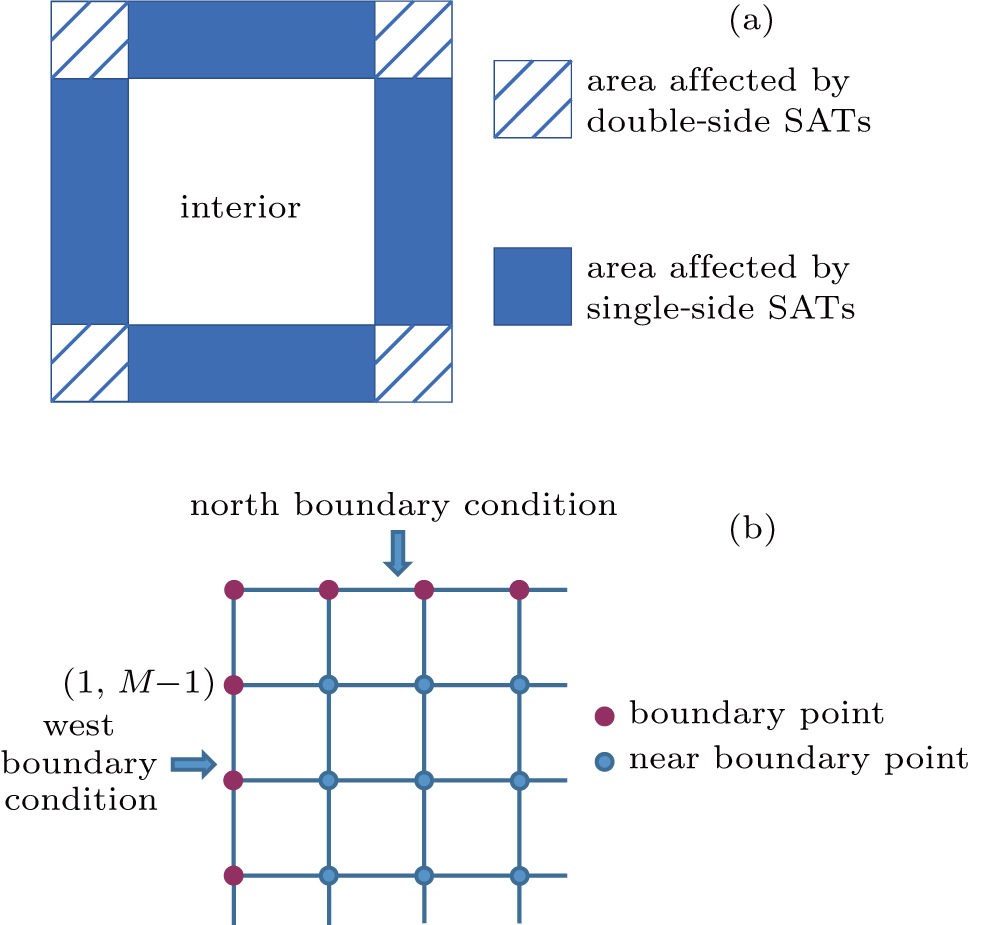
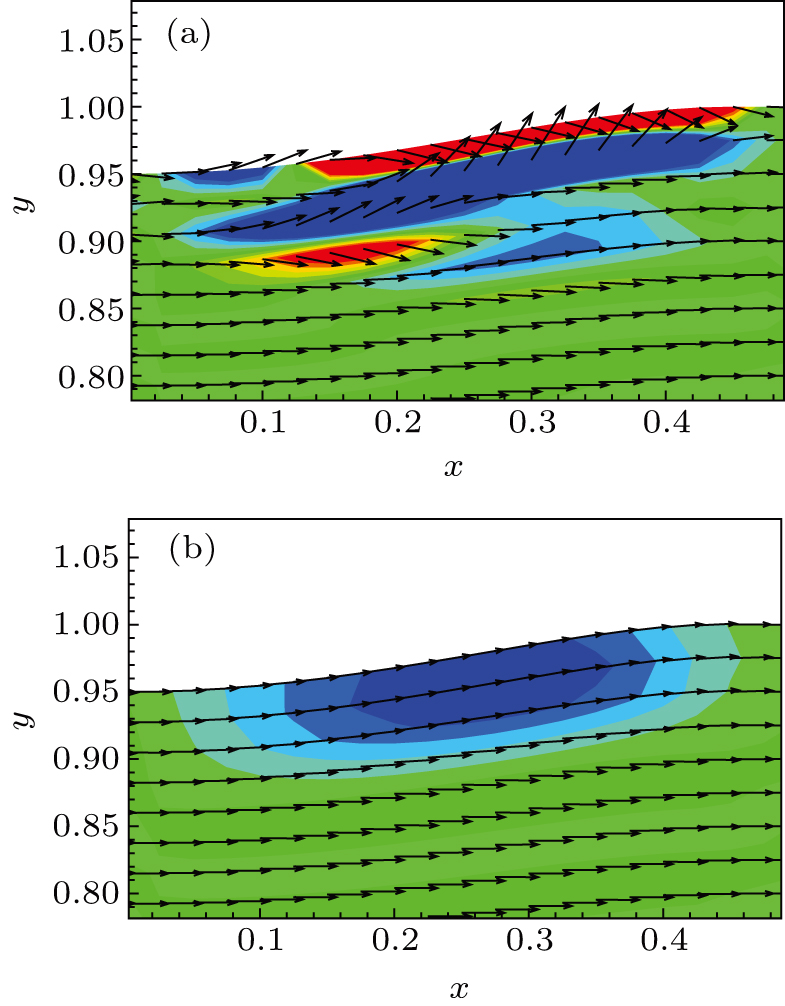
t=6.3 the vortex is almost broken. This phenomenon indicates that some modifications for the scheme should be made to dissolve the non-physical error emerging from the corner regions, where the SATs from two boundaries overlap; see Fig.
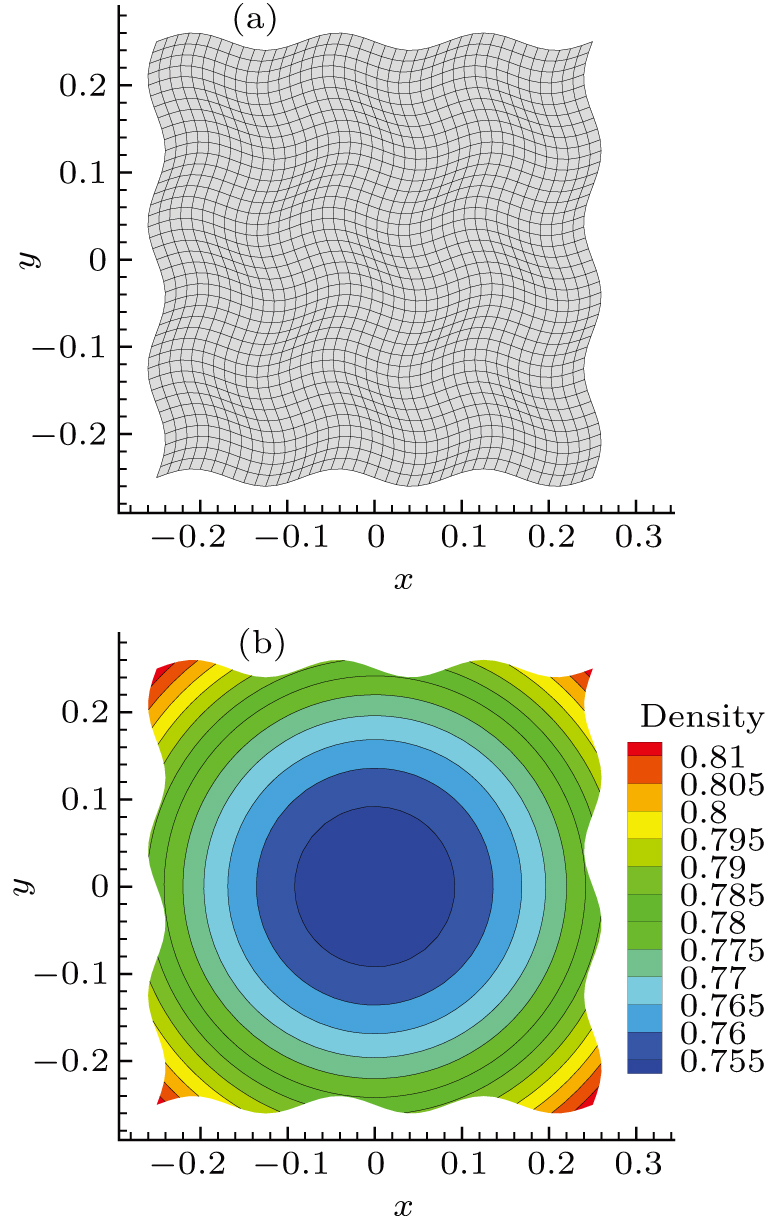
2(a).
To show how to improve the scheme, we take as an example the solution point
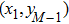 at the west–north corner; see Fig. 2(b). The semi-discrete approximation (9) at this point reads
at the west–north corner; see Fig. 2(b). The semi-discrete approximation (9) at this point reads
Here the first penalty term imposes weakly the west boundary condition, whereas the second one imposes the north boundary condition. It is noted that the solution point
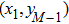
resides on the west boundary, which means that the second penalty term is not so important here. In this regard, we adjust the coefficient of the first penalty coefficient
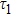
to weaken the effect of the second one, while other coefficients remain unchanged. The same reasoning applies for other similar points. In this paper, we choose the penalty coefficients to be
for the scheme of Eqs. (
6)–(
14), although the choice may be optimized further.