Stabilized seventh-order dissipative compact scheme for two-dimensional Euler equations
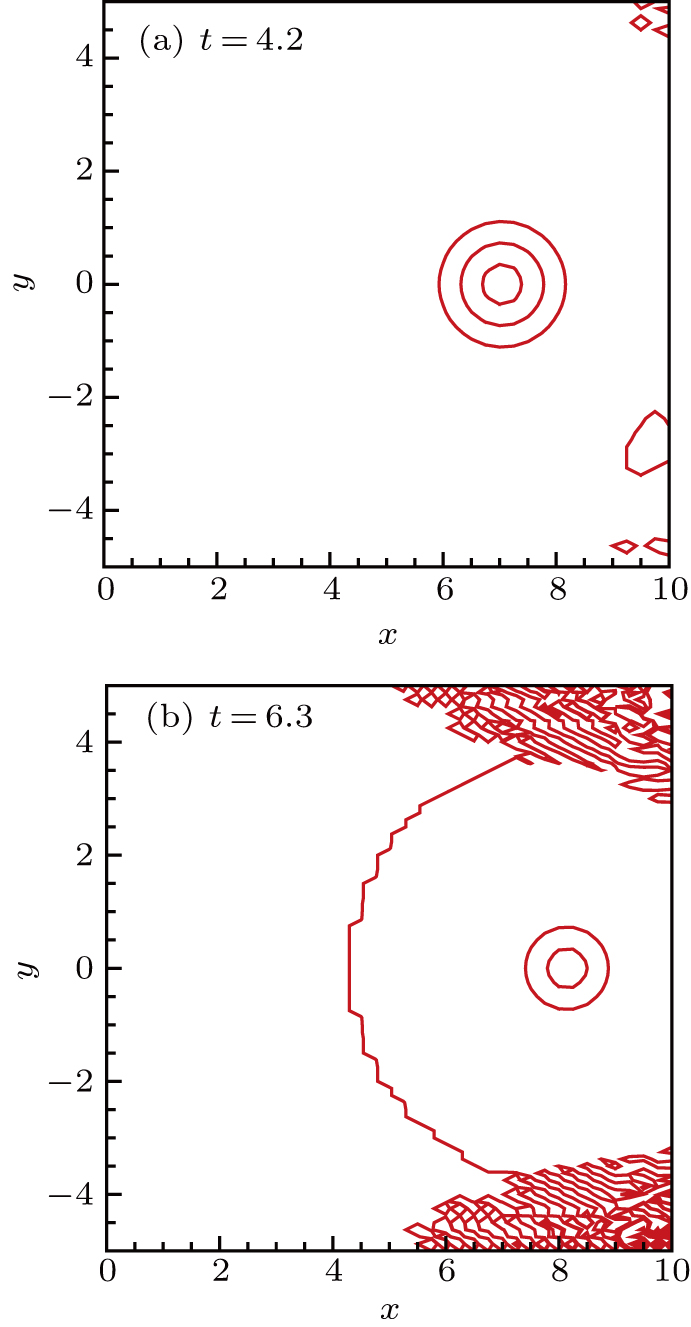
Density contours of the vortex obtained by the scheme of Eqs. (
Stabilized seventh-order dissipative compact scheme for two-dimensional Euler equations |
|
Density contours of the vortex obtained by the scheme of Eqs. ( |
 |