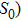† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 91750104, 11534004, 11874179, 11127403, 11474130) and the Natural Science Foundation of Jilin Province, China (Grant No. 20180101289JC).
We investigate experimentally multi-orbital effects in high-order harmonic generation (HHG) from aligned CO2 and N2O molecules by intense femtosecond laser fields with linear and elliptical polarizations. For either of the aligned molecules, a minimum in the harmonic spectrum is observed, the position of which shifts to lower-order harmonics when decreasing the intensity or increasing the ellipticity of the driving laser. This indicates that the minimum originates from the dynamic interference of different channels, of which the tunneling ionization and recombination are contributed via different molecular orbitals. The results show that both the highest occupied molecular orbital (HOMO) and low-lying HOMO-2 in CO2 (or HOMO-1 in N2O) contribute to the molecular HHG in both linearly and elliptically polarized strong laser fields. Our study would pave a way for understanding multi-electron dynamics from polyatomic molecules irradiated by strong laser fields.
The interaction of strong laser radiation with atoms or molecules results in various non-perturbative and highly nonlinear phenomena, such as high-order above threshold ionization (HATI),[1,2] non-sequential double (NSDI) and multiple ionization,[3] neutral high Rydberg state excitation (RSE),[4] and high-order harmonic generation (HHG).[5,6] Among them, HHG has attracted intense research interest, due to its potential applications as tabletop coherent radiation source in the extreme ultraviolet (XUV) and soft x-ray regions,[7] as well as attosecond pulses.[8–12] HHG facilitates measurements that could resolve electronic structure[13,14] and dynamic processes[15,16] on sub-femtosecond time scale and with sub-nanometer spatial resolution.
The physical picture of atomic HHG in a strong laser field is a well-known semi-classical three-step model:[17] (i) tunneling ionization of electrons in an atom or molecule, (ii) the quasi-free electrons are accelerated in the intense laser field, (iii) the high energy electrons recombine with the ionic core to emit redundant energy as coherent XUV photon flux. Molecules have much more complicated structures than atoms, which have multicenter and diverse geometric structure, large density of electronic states with different symmetries, as well as additional nuclear rotational and vibrational motions, providing extra parameters to control HHG.[18–20] By studying HHG of aligned molecules, several experimental and theoretical observations[21–25] have identified that both ionization and recombination are dependent on the symmetries of the highest occupied molecular orbital (HOMO) and even lower-lying molecular orbitals (HOMO-1, HOMO-2, 
Here we experimentally investigate and compare the HHG spectra from aligned triatomic molecules CO2 and N2O by femtosecond strong laser field. While both molecules are linearly structured, N2O is asymmetry triatomic molecules with a 


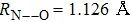
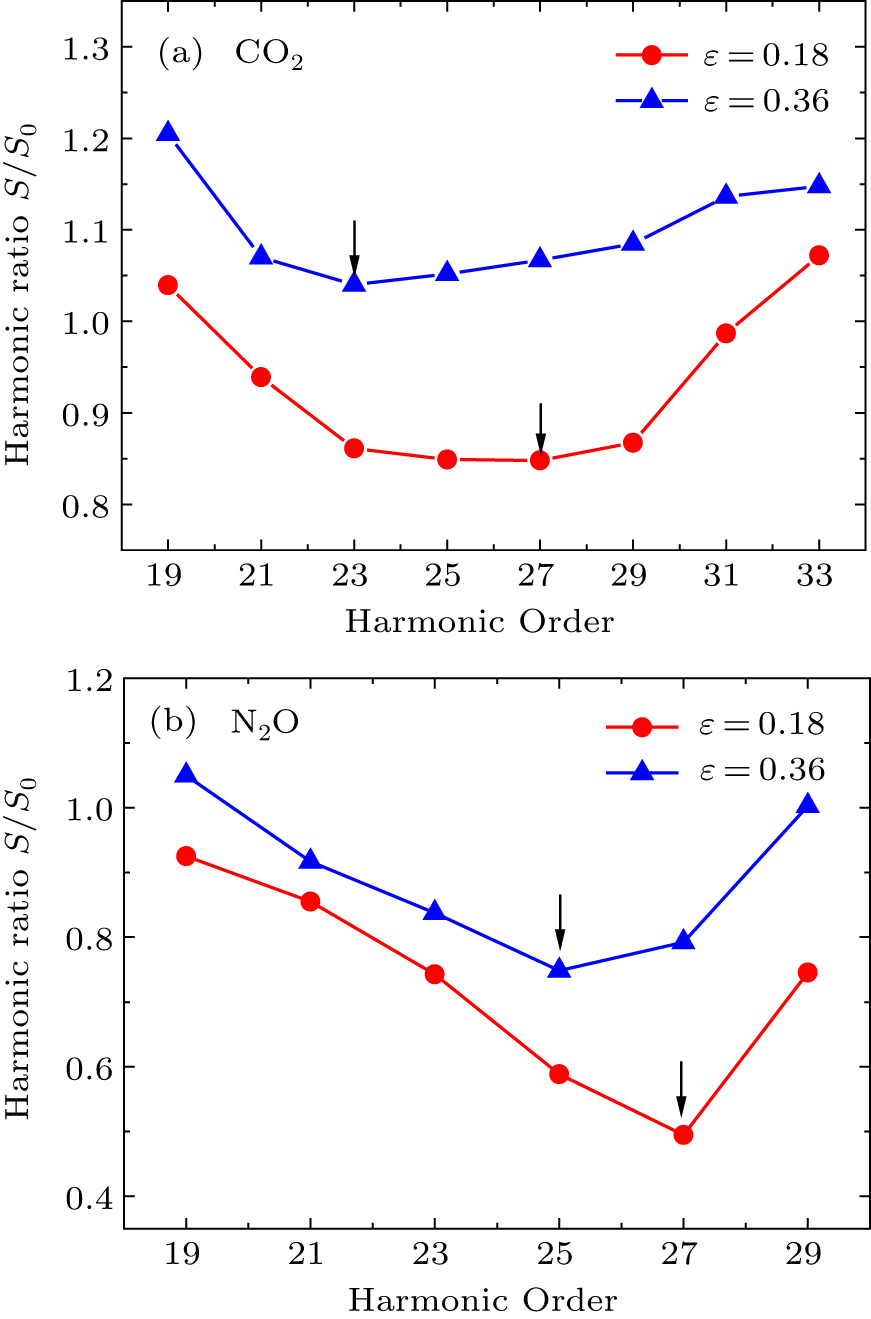
There are some studies that have been reported on the molecular structure and multi-electron dynamics of HHG from CO2 or N2O.[15,28–30] Smirnova et al.[15] have reported the minimum position of the HHG spectra in CO2 molecules which is related to the intensity of the driving laser. This observation is interpreted in terms of the destructive interference from different molecular orbitals (HOMO and HOMO-2) for high-harmonic emission. Wörner et al.[28] have observed that the positions of the minima of harmonic spectra from aligned CO2 shifted by over more than 15 eV with the change of both wavelength and intensity of the driving laser. Rupenyan et al.[29] investigated the effects of electronic structures and multi-electron dynamics on the harmonic spectra from CO2 and N2O by using near-infrared driving laser fields in the wavelength range of 


In our study, we investigate and compare HHG of aligned CO2 and N2O molecules in both linearly and elliptically polarized laser field. The harmonic yield is measured with different intensity and ellipticity of the driving laser field. Based on our experimental observations, we discuss the multi-orbital effects and multi-electronic dynamics on HHG from aligned CO2 and N2O in strong laser fields.
The experimental setup used for generation and detection of HHG has already been described in our previous work.[32–34] Briefly, a Ti: sapphire laser system operating at 1 kHz repetition was used to deliver ∼35 fs pulses centered at 800 nm. The output pulse is divided into two parts by using a 30:70 beam splitter. One laser beam with lower energy (aligning laser) was used to excite rotational energy levels and form rotational wave packets of CO2 or N2O molecules. The other beam with higher energy (driving laser) was used to drive the aligned molecules to generate harmonics. The ellipticity of the driving laser was changed by a combination of an adjustable zero-order half-wave plate placed before a zero-order quarter-wave plate with fixed optic axis. This configuration minimizes the diffraction efficiency of spherical grating affected by the polarization of HHG. A motorized delay stage was inserted into the path of driving laser to control the relative delay time between the two laser pulses. A half-wave plate and a Glan-laser polarizer were placed in the path of each laser beam to adjust its intensity. The polarization angle Θ between the aligning and driving lasers was adjusted by using a half-wave plate placed in the path of the aligning laser. After focused by a focal length 300 mm, the aligning laser and the driving laser were collinearly sent into the gas zone to align the molecules and generate harmonics. The intensity of the aligning laser at the interaction region was about 7×1013 W/cm2. The backing pressure of CO2 or N2O (gas purity at 99.999%) gases was 2 bar. The gaseous samples were continuously expanded into the interaction vacuum chamber through a 
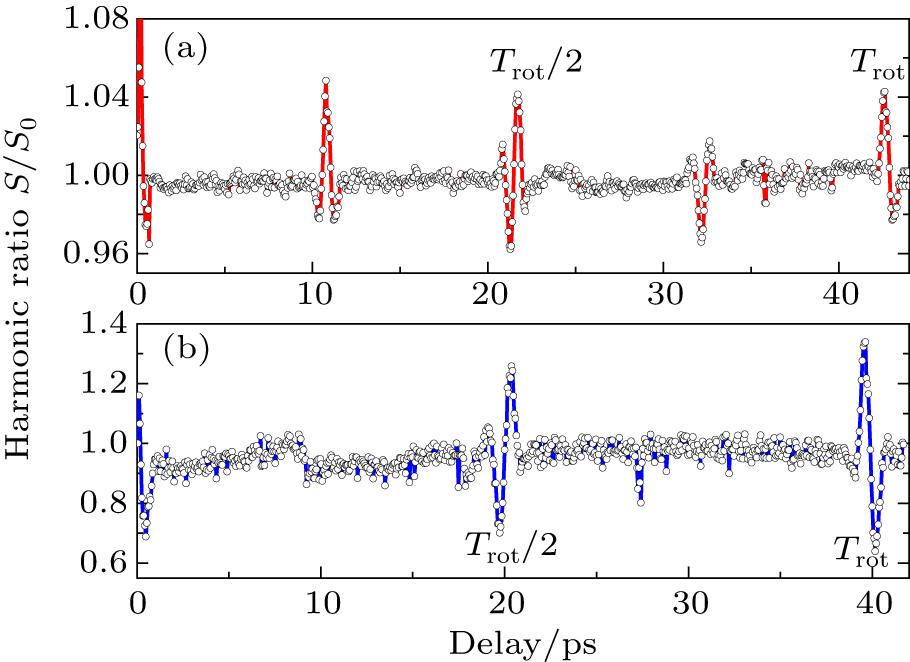
In our study, we investigate the harmonics from aligned molecules by varying the driving laser intensity and polarization, which would add our understanding on the multi-orbital effect of molecular HHG. We first investigate the alignment of molecules by measuring the harmonic intensities on the delay time between the aligning and driving lasers. The polarization of the two lasers are set to be parallel to each other. The results for the 27th harmonics for CO2 and N2O molecules are shown in Fig. 
In Fig. 
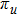

 | Fig. 3. Orbital structures of HOMO, HOMO-1, and HOMO-2 of CO2 (a)–(c) and N2O (d)–(f) calculated by the DFT method at the B3LYP/6-311++G** level. |
The effect of such destructive interference, also known as dynamic interference, replies on the phase difference of HHG from the two different channels. The phase is determined by the delay time between the tunneling ionization and recombination, which depends on the intensity of the driving laser field. Thus the minimum in harmonic spectrum shifts as the laser intensity is changed. The intensity-dependent interference from different channels in HHG of CO2 molecules has been discussed in detail in the pioneer paper by Smirnova et al.[15] The results in Fig.
We further investigate the harmonic intensities from aligned CO2 and N2O molecules in elliptically polarized driving laser field. Figure 

In this work, we have performed an experimental investigation on the multiple orbitals effect in the HHG from aligned CO2 and N2O molecules by both linearly and elliptically polarized strong laser field. The position of the minimum in the HHG spectra could be shifted by the intensity and ellipticity of driving laser. The reason was interpreted as the dynamic interference of HHG from the HOMO and HOMO-2 in CO2 (or HOMO-1 in N2O). Our research results would shed some light for further studies on the multi-orbital effect in the interaction of molecules with strong laser fields.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] |