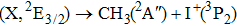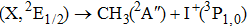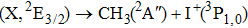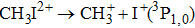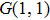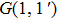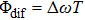† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11374124).
Coherent control of fragmentation of CH3I using shaped femtosecond pulse train is investigated. The dissociation processes can be modulated by changing the separation of the shaped pulse train, and the yield of I+ under the irradiation of the optimal pulse is significantly increased compared with that using the transform-limited pulse. We discuss the control mechanism of dissociation processes with coherent interference in time domain. A three-pulse control model is proposed to explain the counterintuitive experimental results.
The control of molecular fragmentation induced by laser is a fundamental goal with many important applications in controlling physical, chemical, and biological processes. The selective breaking and reforming of chemical bonds are the key of molecular fragmentation control, which can be used to exclusively acquire the desired products. However, due to the complexity of the molecular structure, it is quite difficult to control the dissociation processes using a single simple infrared laser pulse. The combination of developed detection techniques and state-of-the art laser manipulation techniques makes the control possible. Many different detection methods have been employed to probe the photodissociation processes, such as time-of-flight mass spectroscopy (TOFMS) with high resolution of species,[1] ion velocity map imaging (VMI),[2,3] and photoelectron photoion coincidence (PEPICO).[4–6] On the other hand, a large variety of laser fields have been used to study the photodissociation dynamics. For instance, the linearly or circularly polarized chirped laser pulses enhanced the dissociation by ladder climbing.[7] A weak ultraviolet (UV) laser combined with an intense infrared (IR) laser could facilitate the dissociation processes.[8] There are also many research works on dissociation processes using extreme ultraviolet laser (XUV),[9–11] single-cycle terahertz laser, and few-cycle laser with controllable carrier envelope phase (CEP).[12,13]
Coherent control is a robust method of controlling dissociation processes using multiple quantum pathways interference, which can enhance the desired process among the different competition processes. In the past, bond-selected chemistry has been extensively studied by both experiment[14,15] and theory.[16,17] For example, the branching ratios of dissociation processes can be manipulated by the dynamic Stark effect,[18] conical intersections induced by laser,[19] and coherent adiabatic passage.[20] The development in laser pulse shaping techniques promotes the coherent control of chemical reactions. By the pulse shaping techniques, one can stretch the pulse from tens of femtoseconds to tens of picoseconds, and modulate the linear chirp and the relative phase of the laser pulses. Therefore, we can design the laser pulses to achieve arbitrary chemical bond breaking by selectively introducing energy into the molecule system. The optimal control theory (OCT)[21] has emerged to achieve the selective control without the prediction of the fragmentation mechanism. The closed-loop optimal feedback control steers the dissociation towards a pre-designed product. So far, there have been many closed-loop control experiments and theories for different molecules.[22] Due to the breakthrough of the few-cycle carrier envelope phase (CEP) stable laser, one can modulate the dissociation processes by controlling the CEP of the ultrafast optical field. For instance, Xie and co-workers[23] found that the variation of CEP can selectively remove the re-scattering energy of special valence electrons and achieve the control of molecular fragmentation processes.
Methyl iodide (CH3I), as a polar molecule with 

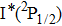
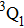
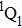

The aim of this work is to investigate the dissociation dynamics of CH3I irradiated by shaped femtosecond pulse trains. By analyzing the kinetic energy releases (KER) of the fragment ion I+, we can identify the DI and CE channels using the transform-limited (TL) and shaped femtosecond pulse train. Moreover, the dissociation process can be modulated by changing the sub-pulse separation, and the yield of I+ irradiated by the optimal pulse is significantly increased compared with that using TL pulse. The modulation mechanism of the dissociation process is discussed based on coherent interference in time domain. A three-pulse control model is proposed to explain the counterintuitive experimental results.
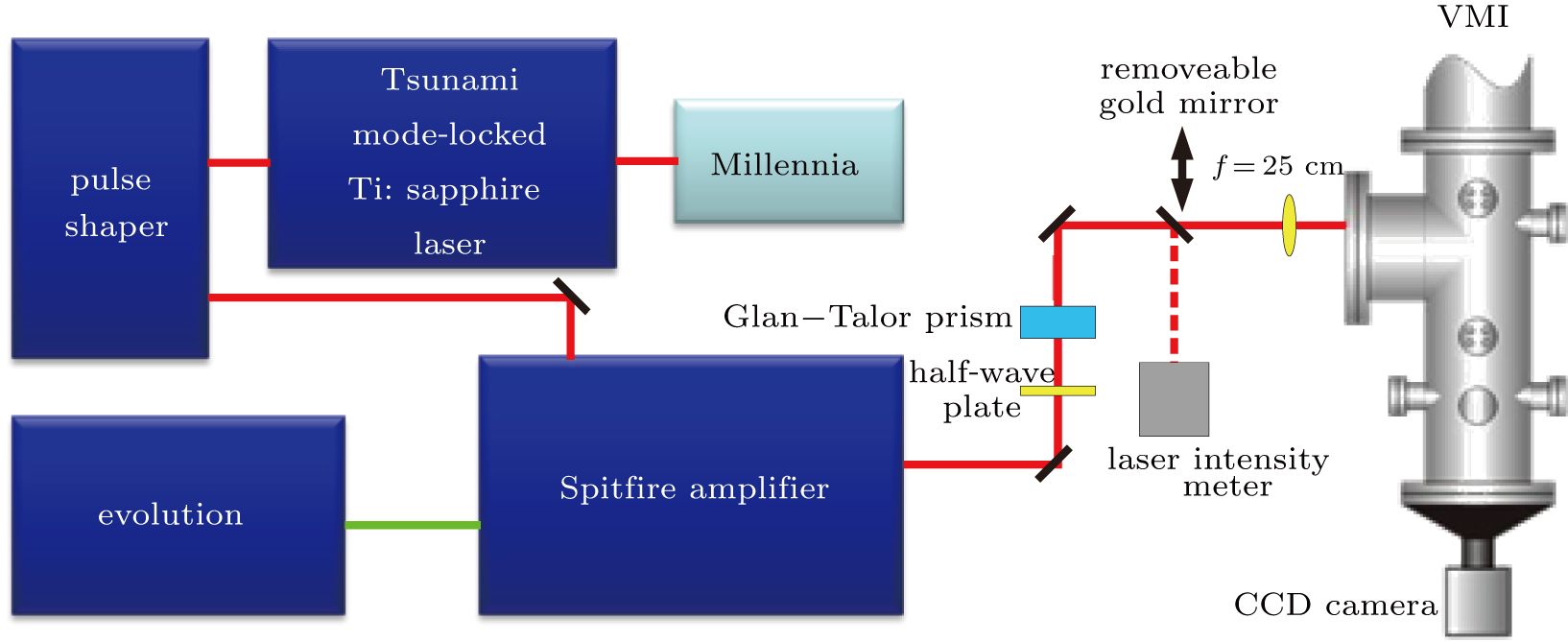
The experimental setup, depicted schematically in Fig.
The laser system is a Ti: sapphire chirped-pulse amplification laser (Millennia feed laser, Spectra-Physics Tsunami oscillator, and Spitfire amplifier) with the central wavelength of 800 nm, the pulse duration of 100 fs, and the repetition rate of 1 kHz. The laser pulse from the oscillator is directed into the pulse shaper and the shaped pulse is generated. Then, the shaped pulse passes through the amplifier, after which the energy of the single pulse can reach 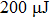
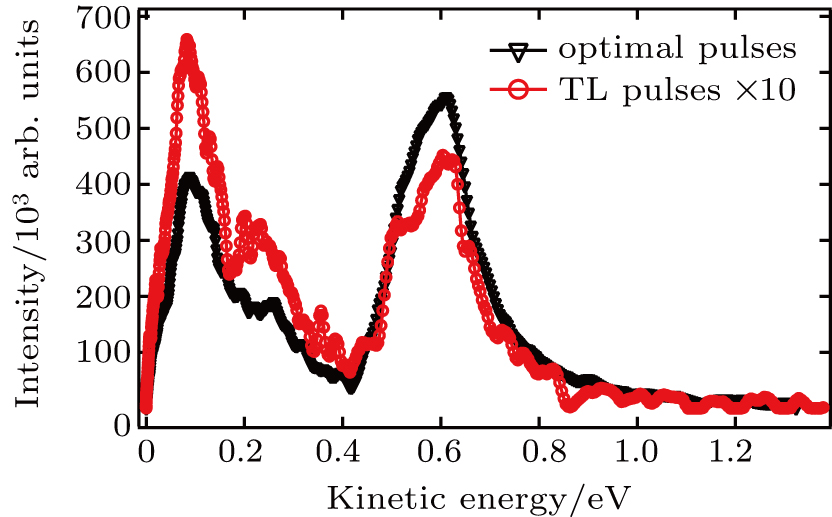
In this section, a detailed analysis of TL laser-induced fragmentation of CH3I is presented. The intensity of the TL pulse at the focal point is about 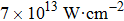
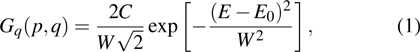 |
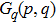
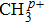
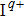
In the following section, each individual channel producing fragment ion I+ is identified. When the intensity of the TL pulse is weak, the dissociation processes of CH3I follow the multiphoton DI mechanism. Therefore, the CH3I molecule is first ionized to produce the parent ion CH3I+, and then dissociated via additional photon absorption. But when the intensity of the TL pulse is strong, the parent ion is continuously ionized to form a higher charged parent ion and then produce the I+ fragment with higher kinetic energy by CE. We define the fragmentation channel of I+ as 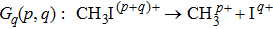
The values of two peaks in the low kinetic energy region from Fig. 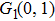
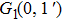
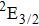
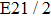
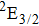
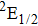
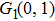
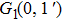

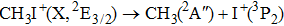
| Table 1.
The calculated I+ KERs of the n-photon dissociation channels of CH3I+ and the observed I+ KERs by Liu et al.,[31] Wang et al.,[32] and in the present work. . |
The values of two peaks in the high kinetic energy region from Fig. 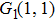

A pulse train with evenly spaced sub-pulses is produced experimentally with the sinusoidal phase function[34]
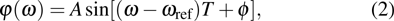 |

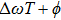
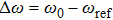
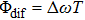
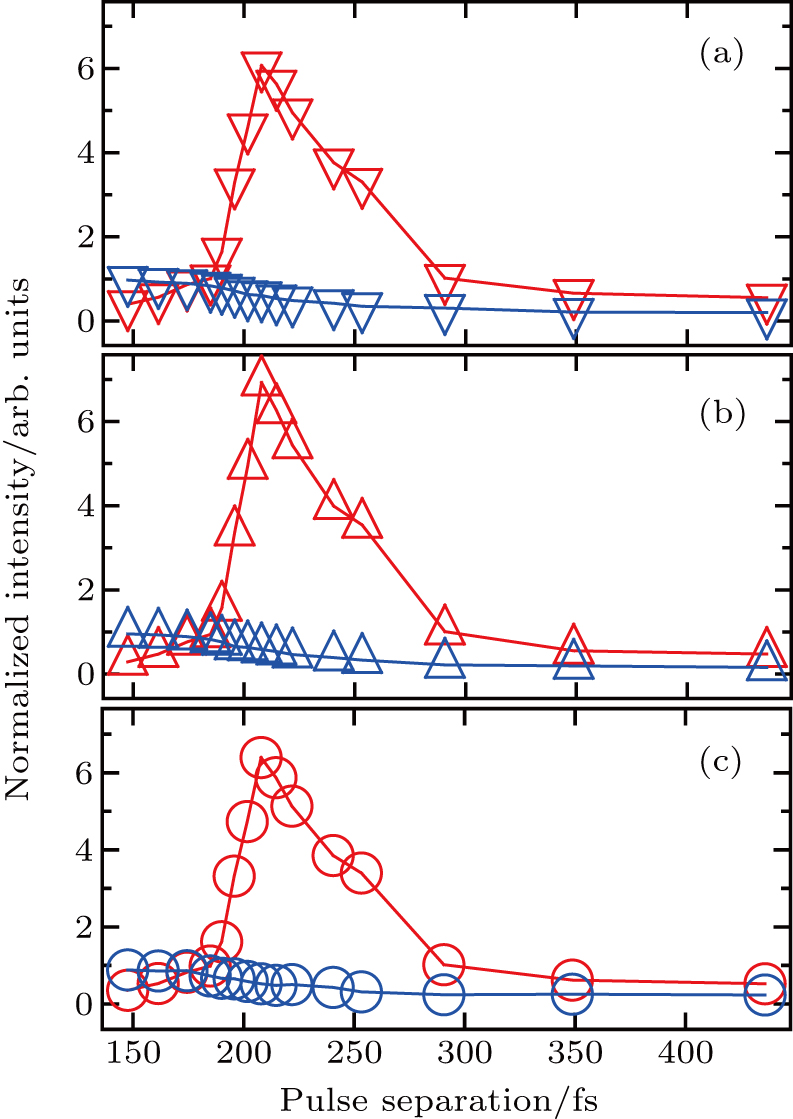
In this section, we present the experimental KER distributions obtained under the shaped pulse train with the same energy as that of the TL pulse. By scanning the value of T from about 150 fs to 440 fs, the KER distributions upon the variation of the pulse separation are mapped in Fig. 
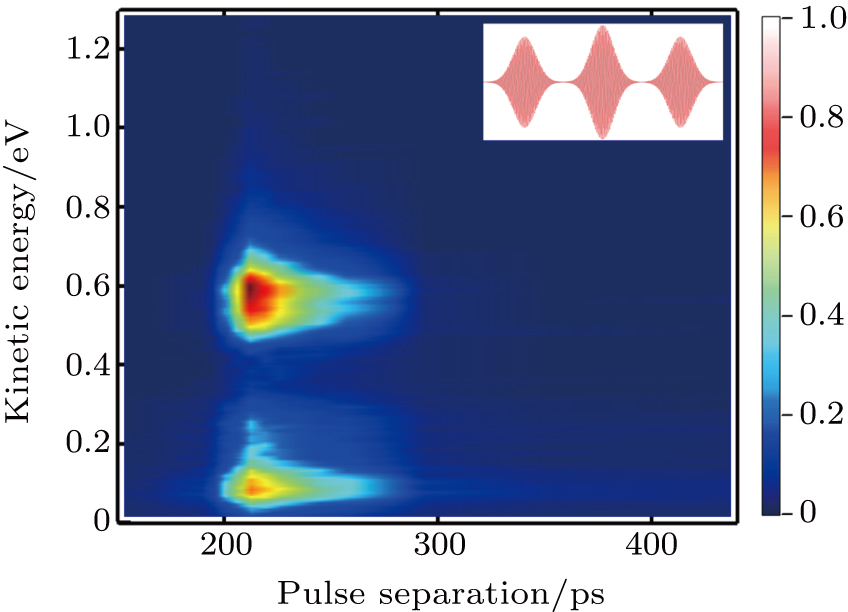 | Fig. 3. The KER distributions upon the variation of the separation of shaped pulse train. The inset is the schematic diagram of the shaped pulse train. |
To investigate the control over different fragmentation channels of I+ using shaped pulse train, we integrate the KER distribution respect to the corresponding peak to obtain the curves of the intensities of different channels with the pulse separation. Since the two peaks of the CE channels overlap, we integrate the two CE channels as one peak, and the same operation is performed for the two peaks of the DI channels. Figure
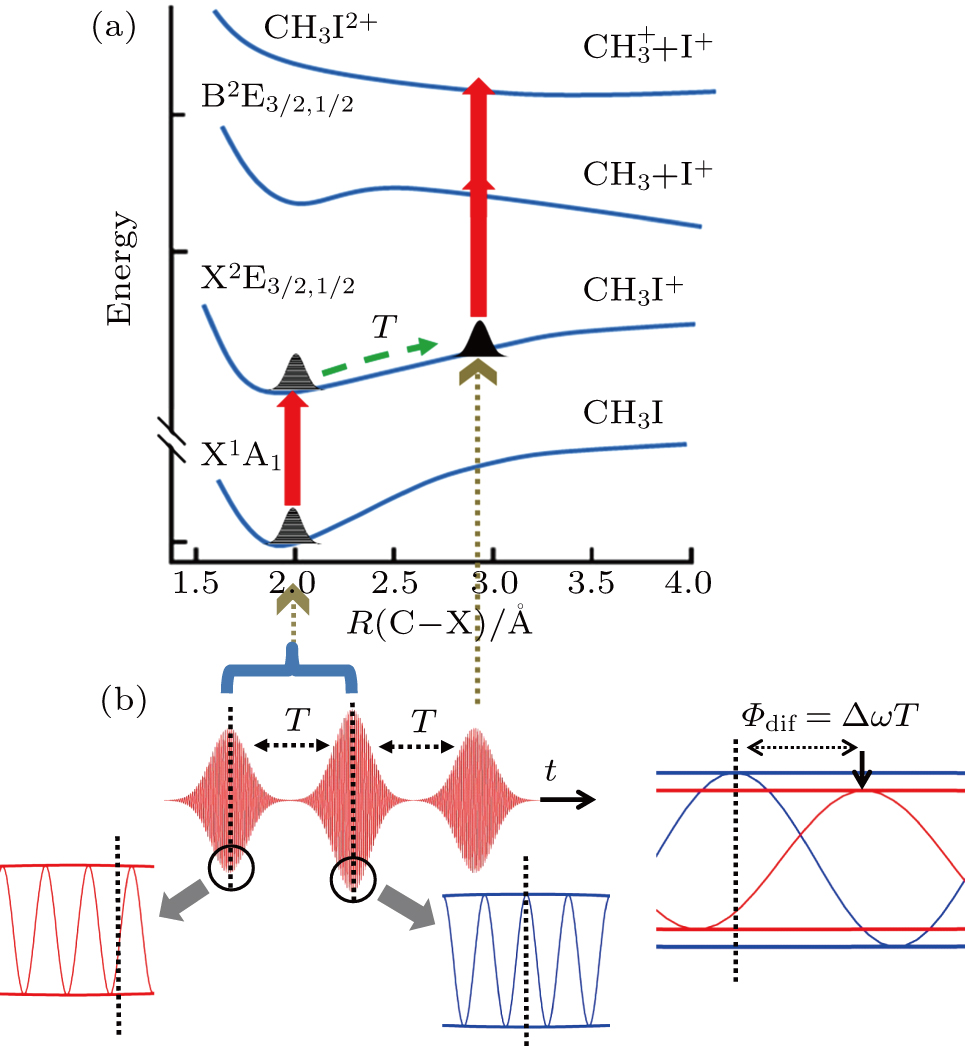
Due to the short pulse duration, the dominant dissociation mechanism is DI. For the shaped pulse train, the equivalent duration is larger than that of the TL pulse. Moreover, because of the effect of multiple sub-pulses, the photodissociation of CH3I in its A-band is likely to happen using the shaped pulse train. The dominant transition in A-band at the wavelength used in the present work is to the 3Q0 state (parallel transition) by absorbing three 800 nm photons, which leads to direct C–I bond cleavage into a methyl radical and a spin–orbit excited iodine atom (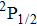
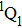

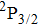
The control mechanism in the present study might be the modulation of A-band photodissociation, which ultimately leads to the modulation of intensity of the I+ fragment ionized from the neutral iodine atom. However, the previous research results have confirmed that the dissociation time of all photodissociation channels from A-band is less than 150 fs.[36] For the optimal pulse train (T = 208 fs) in the present study, the photodissociation processes have already been completed before the arrival of the subsequent sub-pulses. Therefore, the control mechanism is not the modulation of the A-band photodissociation.
One possible way to rationalize the counterintuitive results is to consider the modulation of ionization processes of CH3I under the irradiation of the shaped pulse train, where a qualitative control mechanism of the three pulses is proposed. This is mainly attributed to two reasons. One is that we did not see the modulation of iodide ionʼs intensity with the delay in the pump–probe experiment in Fig. 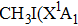
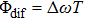

 |
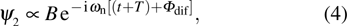 |
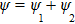
 |
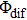
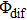
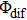
Therefore, for the three pulses control mechanism, the former two sub-pulses are the key to the modulation of yield of fragment ion I+ for the DI channels. With the movement of the wave packet on the potential energy surface, the delay T determines the photon energy of the transition from X2E3/2, 1/2 to dissociation state B2E3/2, 1/2. After the unique delay of T, the third sub-pulse arrives and maximizes the fragmentation. The two processes of ionization interference and maximizing dissociation work together and lead to the modulation of the I+ fragment yield. This is the reason that the peak intensities of KER distribution in Fig. 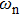
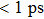
Compared with the case under the TL pulse, the increase in intensity of CE channel is almost the same as that of DI channel using the shaped pulse train in Fig.
We perform a study of coherent control on fragmentation of CH3I by shaped femtosecond pulse train. The dissociation channels of fragment ion I+ using TL pulse are identified via the analysis of KER distribution. By changing the separation of the shaped pulse train, the modulation of the KER distribution of I+ fragment is achieved. Moreover, it is the optimal pulse train (with T = 208 fs) that makes the intensities of dissociation channels simultaneously reach the maxima. Compared with the TL pulse, both yields of DI and CE channels significantly increase. A three-pulse control model is proposed to explain the counterintuitive experimental results. We believe that the modulation of ionization processes leads to the control over fragmentation of CH3I using the shaped pulse train, The assembly of ionization processes is the coherent interference between the two independent wave packets excited by the two ionizing pulses in the time domain. When T and 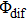
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] |