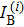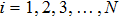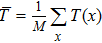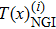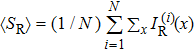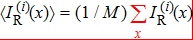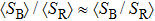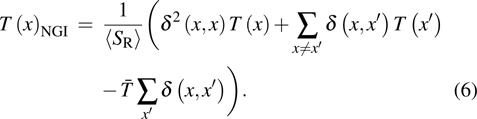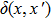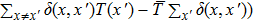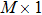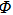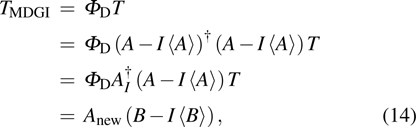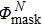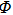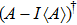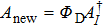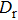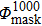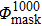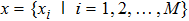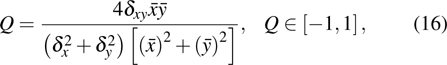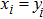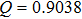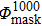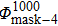1. IntroductionIn recent years, ghost imaging (GI) has attracted considerable attention due to its ability to reconstruct an unknown object through spatial intensity correlation measurements from tow detectors. Unlike the traditional imaging methods, one of the detectors without spatial resolution is needed in ghost imaging to contain the object information. The other detector with spatial resolution is employed to detect the light source. Quantum ghost imaging was first theoretically introduced by Klyshko and demonstrated experimentally by Pittman[1,2] in 1995. Afterwards, it was discovered that pseudo-thermal light sources[3–5] and thermal light sources[6] can be exploited to achieve GI. Now, researchers are working towards the progress from pure theory to real-world applications.
Recent research has revealed that GI has received increasing attention due to its novel physical characteristics, such as non-lens imaging, atmospheric turbulence free, etc.[7–10] These studies demonstrated that GI is a very powerful tool for imaging objects in optically harsh fields such as lidar detection, three-dimensional (3D) imaging, biomedical imaging, etc.[11–23] Unfortunately, the limitation of signal-to-noise ratio (SNR) and resolution are an obstacle for GI to use pseudo-thermal light, which is difficult to meet practical application requirements. Therefore, improving GI image quality with fewer measurements is the crucial problem to be resolved. In order to address this issue, many novel reconstruction methods have been proposed.[24–35] In Ref. [24], the normalized ghost imaging (NGI) with a more appropriate weighting factor is applied to the ensemble average of the estimated object, and has a similar performance to the differential ghost imaging (DGI).[25] Besides, the iterative denoising of ghost imaging (IDGI)[26–28] shows a remarkable enhancement in terms of reconstruction quality by estimating the noise terms via the conventional GI algorithm. However, the IDGI relies on the quality of the original GI reconstruction image. Comparing with the above methods, the reconstruction quality of compressive-sensing ghost imaging (CGI)[29–32] shows significant improvement and lower measurements than Nyquist sampling limit. However, it may rely on the prior character of the object, and the optimization procedure itself is time-consuming and memory-wasting. Though pseudo-inverse GI (PGI)[33,34] is likely to enhance the visibility and spatial resolution of GI with respect to the property of the pseudo-inverse matrix, it cannot acquire the robust images in practical engineering applications. Instead of optimizing the speckle pattern, scalar-matrix-structured[35] GI demonstrates a robust reconstruction image. However, this method lacks universality in practical applications and does not give a method of constructing an effective scalar matrix either.
In this paper, a mask-based denoising ghost imaging (MDGI) method is proposed, which aims to remove the correlated noise in GI and improving the quality of the reconstructed image. This method has better imaging quality than DGI and NGI. Compared with IDGI, it does not depend on the quality of the original GI methods. Compared with the SMGI method, an effective construction method of the new measurement matrix is given. Firstly, we theoretically analyze the reason why the SNR of DGI and NGI are both higher than that of GI. Then, we use the OTSU[36] method to calculate the optimal threshold corresponding to the correlated noise in GI. Finally, the mask is obtained by combining the calculated optimal threshold with that from a dilation method, and it is used to further reduce the correlated noise in GI. From simulations and experimental results, we can conclude that our method can effectively remove the correlated noise in GI and improve the imaging quality index compared with GI, DGI and NGI method.
2. Principle and methodsA schematic of the ghost imaging is shown in Fig. 1(a). The laser beam is expanded by lenses L2 and L3, projecting onto a slowly rotating ground glass to produce a pseudo-thermal light source. After passing through a beam splitter (BS), the pseudo-thermal light is divided into two paths: the probe path and the reference path. In the probe path, the probe beam goes through a transmission object T(x) and the total intensity is collected by the object detector D1 (bucket detector) after passing through lens L1, recorded as IB. In the reference path, the reference beam propagates directly to a reference detector D2 (CCD camera). The reference light intensity distribution can be recorded as IR(x) by detector D2. Then, the object image can be reconstructed by computing the intensity correlation of two light beams. In the conventional ghost imaging (GI), the second-order correlation fluctuation function is[37]
where
x represents the transverse spatial coordinate,

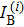
denotes the total light intensity collected by bucket detector with
i-th measurement;
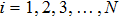
, and
N denotes the total number of measurements;

refers to the reference light intensity distributions collected by CCD in
i-th measurement. The covariance of the light field at the
x and

point is defined as
Equation (
1) can thus be expressed as
where
M denotes the total number of pixels of the object, and

represents autocorrelation coefficient.

can be considered as a noise term in GI. Then DGI can be expressed as
[26]Here,
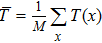
.
Moreover, the reconstructed object
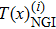 by NGI in ith measurement is expressed below
by NGI in ith measurement is expressed below
where

,
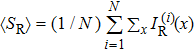
,

, and
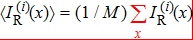
. When measurements are enough,
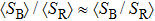
. Therefore,
We can conclude from this analysis that the covariance
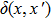 gives rise to the low SNR imaging results in GI, both DGI and NGI can suppress covariance
gives rise to the low SNR imaging results in GI, both DGI and NGI can suppress covariance
 (
(
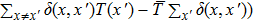 in GI to improve the quality of image. To effectively improve the quality of image better than DGI and NGI, we attempt to adopt a mask to effectively eliminate the elements
in GI to improve the quality of image. To effectively improve the quality of image better than DGI and NGI, we attempt to adopt a mask to effectively eliminate the elements
 , which are considered as correlated noise.
, which are considered as correlated noise.
The speckle field of the i-th measurement is reshaped as a row vector
 of size 1×M. After N measurements, we can obtain an N × M measurement matrix denoted as A, which can be expressed as follows:
of size 1×M. After N measurements, we can obtain an N × M measurement matrix denoted as A, which can be expressed as follows:
Consequently, equation (
1) can be expressed as follows:
where

, T represents the transmission coefficient of the original object and is an
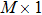
column vector, and

. In addition,
I denotes an

column vector whose elements are all 1 and

denotes the average of each column of
A and is an 1×
M row vector. Since matrix
A is not an orthogonal matrix, the utilization of information is low. Under the condition of

, the covariance matrix cov(
A) will approach to a diagonal matrix. This is the fundamental reason for the improvement of imaging SNR. In order to reduce the number of measurements and improve SNR, we construct a mask with OTSU method to remove the correlated noise from the covariance matrix cov(
A). Setting
Φ = cov(A),normalizing matrix
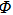
by Eq. (
9) can be expressed as follows:
Here, Φmax is the maximum value of the matrix Φ. Simultaneously, we need to set a valid threshold tm to separate Φnorm into two parts as given below.
We can consider that the coordinate of the element value 0 in the mask matrix
 corresponds to the position of the correlated noise in the matrix Φ. We will next describe how to set the optimal threshold tm by the OTSU method.
corresponds to the position of the correlated noise in the matrix Φ. We will next describe how to set the optimal threshold tm by the OTSU method.
where
μ denotes the average value of the matrix
Φnorm and
g is the variance between classes. Let
K represent the number of elements of the matrix
Φnorm, then
K =
M×
M. The number of the parts less than
t is
K0 and the average value of the corresponding elements is
μ0, the number of other parts is
K1 and the average value is
μ1, and
K =
K0+
K1. Moreover,

and

. Through Eqs. (
11) and (
12), the between-class variance
g can be expressed as
When the between-class variance
g is maximum, we can obtain the optimal threshold
tm. Therefore, our method can be defined as
where

(
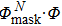
denotes the point multiplication operation between matrices
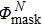
and
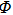
) and matrix
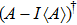
represents the pseudo-inverse operation of

. It should be noted that in our method

is replaced by
Anew (
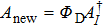
) compared with traditional GI method in Eq. (
8). In addition, both mask

and matrix
Anew can be obtained through the idle reference detector measurements in engineering applications.
As a preliminary verification of the advantages of our method, we first construct matrix Anew through using Eq. (14). Results for Φ and Φ1 are shown in Figs. 2(a) and 2(b), we note that the values of the off-diagonal elements in Φ are significantly greater than those in Φ1, which explains that the correlated noise caused by off-diagonal elements in Φ is further removed.
Let
 and
and
 be the sets in
be the sets in
 , then the binary dilation of
, then the binary dilation of
 by
by
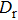 , denoted as
, denoted as
 , will be defined as the set operation:[38,39]
, will be defined as the set operation:[38,39]
where

denotes the Minkowski addition and

is the reflection of the disk-shaped structuring element

with a radius of
r. In other words, it is the set of element locations
z, where the reflected structuring element overlaps with foreground elements in

when translated to
z.
As shown in Fig. 4(a), we can suppress the correlated noise down to a value smaller than the threshold T (
 ) by the mask
) by the mask
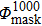 . But accounting for correlated noise, it is likely to influence the calculation of the ideal threshold. To our knowledge, the dilation method can be used in mask
. But accounting for correlated noise, it is likely to influence the calculation of the ideal threshold. To our knowledge, the dilation method can be used in mask
 to add elements at region boundaries and to connect the disjoint parts. Thus, we try to consider modifying mask
to add elements at region boundaries and to connect the disjoint parts. Thus, we try to consider modifying mask
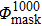 through the dilation method to appropriately increase the width of L (L represents the number of elements whose peak value is greater than the threshold T). The elements used for imaging can be effectively retained by mask
through the dilation method to appropriately increase the width of L (L represents the number of elements whose peak value is greater than the threshold T). The elements used for imaging can be effectively retained by mask
 results for further improving imaging quality, which is consistent with the results indicated in Table 1 and Fig. 4(d). These results demonstrate the advantage of the proposed method. However, by observing the curve in Fig. 4(d), the Q value first increases and then decreases with radius r increasing. As
results for further improving imaging quality, which is consistent with the results indicated in Table 1 and Fig. 4(d). These results demonstrate the advantage of the proposed method. However, by observing the curve in Fig. 4(d), the Q value first increases and then decreases with radius r increasing. As
 , the image quality will be lower than r = 0. This is mainly because when the radius
, the image quality will be lower than r = 0. This is mainly because when the radius
 , the constructed mask will retain more correlated noise, so that the reconstructed image quality deteriorates. Next, we will set the radius r to 5.
, the constructed mask will retain more correlated noise, so that the reconstructed image quality deteriorates. Next, we will set the radius r to 5.
Table 1.
Table 1.
 Table 1.
Reconstruction image PSNR and quality index Q based on different masks in Fig. 3.
.
| Figure |
3(a) |
3(b) |
3(c) |
3(d) |
3(e) |
3(f) |
| r
|
0 |
1 |
2 |
3 |
4 |
5 |
| PSNR/dB |
16.3960 |
16.8108 |
16.9821 |
17.1008 |
17.1048 |
17.2131 |
| Q
|
0.8075 |
0.8300 |
0.8404 |
0.8456 |
0.8456 |
0.8486 |
| Table 1.
Reconstruction image PSNR and quality index Q based on different masks in Fig. 3.
. |
Let
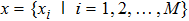 and
and
 be the original object image and the reconstruction image, respectively. The image quality index is defined as[31,40]
be the original object image and the reconstruction image, respectively. The image quality index is defined as[31,40]
where
The best value 1 is achieved if and only if
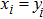
, for all

. The lowest value of -1 occurs only when

. However, the
Q value is generally not less than 0. The peak signal-to-noise ratio (PSNR) is defined as
Here, MSE represents the mean square error of the original object and the reconstructed image, and MAXI is the maximum pixel value of the original image. The bigger the PSNR value, the better the quality of reconstruction image is.
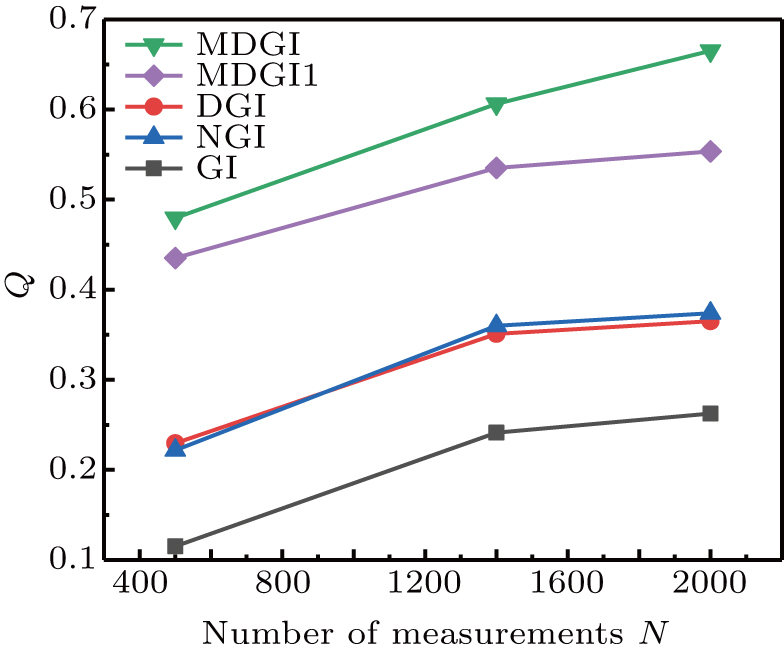
Figure 5 displays the simulation results of “double-slit” with GI, DGI, NGI, MDGI-mask1, and MDGI-mask2 with N measurements. Figure 6 shows the curves of Q values from different methods based on the results presented in Fig. 5. We can find that the observations are consistent with the calculated quality results. The GI, DGI, NGI image are blurry due to background noise interference. Instead, our method can remove the background noise and obtain high-quality image. In addition, the performances of reconstruction quality based on different masks are demonstrated in the inset. In fact, MDGI-mask1 is the MDGI method. However, the mask2
 is a new mask reconstructed according to the reconstruction mask procedure as the above, which is updated under different measurements. We can find that the MDGI shows almost the same performance as MDGI-mask2. In addition, The Q value of the MDGI (N = 2000,
is a new mask reconstructed according to the reconstruction mask procedure as the above, which is updated under different measurements. We can find that the MDGI shows almost the same performance as MDGI-mask2. In addition, The Q value of the MDGI (N = 2000,
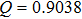 ) reconstructed image is almost the same as that of MDGI (N = 5000, Q = 0.912). Therefore, we directly use mask1
) reconstructed image is almost the same as that of MDGI (N = 5000, Q = 0.912). Therefore, we directly use mask1
 instead of mask2
instead of mask2
 and the number of measurements is set to 2000 to avoid extra calculations in this paper.
and the number of measurements is set to 2000 to avoid extra calculations in this paper.
As shown in Figs. 7(a) and 7(b), the object can hardly be distinguished from GI images. Although the DGI and NGI reconstructed images are better than GI, the PSNR and Q value of the reconstructed image are still too low due to the interference by background noise, which is also consistent with the visual observation. However, the reconstructed image obtained by MDGI can effectively remove the background noise, and the obtained image has the higher PSNR value and Q value. It should be noted that the MDGI uses the dilation method and the MDGI1 does not, and finally the MDGI gets better results than the MDGI1. Meanwhile, the Q-fitting curves from the five methods with different numbers of measurements are shown in Figs. 8(a) and 8(b). It can be observed that the MDGI obtains a higher Q value than the other methods under the same number of measurements. This implies that our method is not only suitable for binary objects but is also suitable for complicated objects.