Zirconia (ZrO₂) is involved in many applications, such as foundry ceramics, refractories, paint pigments, fuel cells, and solid electrolytes in oxygen sensors, due to its outstanding chemical and physical properties including high hardness, high thermal conductivity, and high ionic conductivity.^[1–3] ZrO₂ has abundant phases at high temperatures: the monoclinic phase can be thermodynamically stable from room temperature to about 1100 °C, and then crystallize into a tetragonal phase at 1100 °C and a cubic phase at 1900 °C.^[4–6] To quench these high-temperature tetragonal and cubic phases to ambient conditions, cations with a valence lower than 4⁺, such as Y³⁺, La³⁺, Mg²⁺, and Ca²⁺ are doped, by which CeO₂/ZrO₂, CaO/ZrO₂, MgO/ZrO₂, and Y₂O₃/ZrO₂ (cubic) solid solutions are formed.

Important technical applications can be found in dopants. For example, transient optical measurements of materials under impact compression usually require different types of optical windows.^[7–9] Dolan et al.^[8] reported a new optical window material based on dopant-stabilized cubic ZrO₂). At present, doping Y₂O₃ to obtain cubic ZrO₂) is a common method.^[10] A low impact pressure experimental study showed that cubic ZrO₂) can be used as an optical window material and is a preferred substitute for sapphire window materials.^[8]

Recently, there has been growing interest in the connection between the electrical properties and microstructures of dopant-stabilized ZrO₂.^[11–14] It is found that Sc₂O₃-stabilized ZrO₂ solid solution with the cubic fluorite structure shows the highest conductivity among all ZrO₂)-based electrolytes.^[15,16] This provides potential to lower the operating temperature of the ZrO₂)-based electrochemical devices, and makes the synthesis of the cubic structure ZrO₂ an attractive goal. With the co-precipitate method, Y₂O₃-stabilized ZrO₂ powders in the cubic structure have been directly synthesized, and the particle size is uniform.^[17,18]

As another state parameter that is independent of temperature and chemical composition, pressure tunes the physical properties of materials by compressing the distance between atoms and modifying the electronic structures.^[19,20] The phase transitions of ZrO₂ under high pressure have been studied systematically with various techniques. It undergoes the phase transition sequence of baddeleyite (MI, monoclinic, space group: 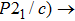orthorhombic I (OI, orthorhombic, space group: Pbca) at 11.8 GPa orthorhombic II (OII, orthorhombic, space group: Pnma) at 26.2 GPa.^[21,22] However, similar studies on dopant-stabilized ZrO₂ solid solutions under high pressures are still lacking. Inspired by the aforementioned issues, we synthesize the Y₂O₃-stabilized ZrO₂ solid solution, and study its electrical transport and structural properties in situ at high pressures. An abnormal change is found in the electrical transport properties, and its physical origin, a pressure-induced isostructural phase transition, is revealed.

ZrO₂/Y₂O₃ samples were prepared by the co-precipitate method. First, a weight of 2.58 g of zirconyl chloride (ZrOCl₂ 8 H₂O) was dissolved in deionized water. Next, 1.56 g YCl₃ was dissolved into the solution to form the Y₂O₃-doped ZrO₂), and then NH₄OH was gradually added to the solution until the pH value was equal to 10. The solution was continuously stirred throughout the process. After reaction, the final product was repeatedly filtered and washed by deionized water to remove the chlorine ions (NH₄Cl), residual NH₃, and other anionic impurities; the product was subsequently settled by centrifugal separation of 10000 rpm for 10 min until the supernatants became clear. After drying at 100 °C for 2 h, the final samples were calcined at 800 °C for 2 h with a heating rate of 5 °C min⁻¹ in a muffle furnace under air atmosphere.

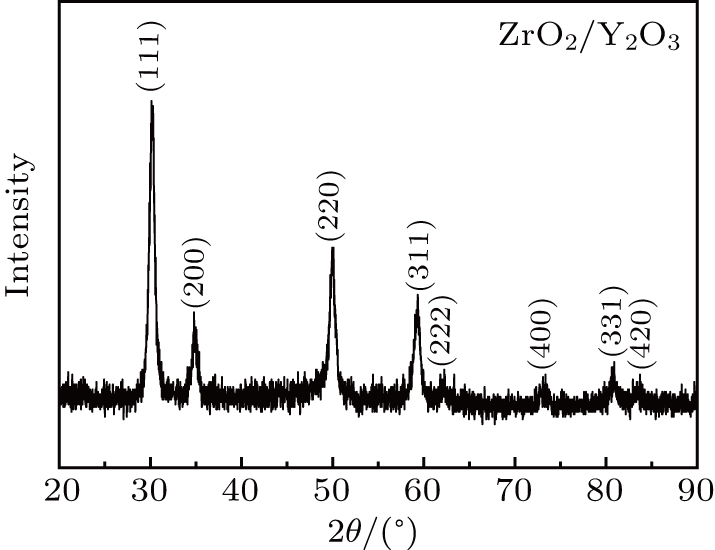
In order to identify the constitution and chemical valences, the samples were further analyzed by x-ray photoelectron spectroscopy (XPS). XPS was done on a PerkinElmer PHI 5000CESCA system to analyze the electronic states. All the binding energies were calibrated via the contaminant carbon (C 1s = 284.6 eV) as a reference. The initial structure of the sample was confirmed by x-ray diffraction (XRD) measurements.

High-pressure experiments were conducted in a diamond anvil cell with the anvil culet with a diameter of .^[23] A piece of T301 stainless steel was pre-indented to a thickness of , and then drilled by a laser to make a hole in diameter at the center of the indentation. A mixture of cubic boron nitride powders and epoxy was compressed into the indentation as the insulating layer. Subsequently, another hole (diameter of ) was drilled and served as a sample chamber. The impedance spectra were measured with parallel plate electrodes. The fabrication process of the electrodes on two diamond anvils has been reported in previous studies.^[24–26] Pressure was calibrated by the shift of the ruby fluorescent R1 line.^[27] No pressure medium was loaded into the sample in order to avoid introducing impurities for the electrical measurement and also to ensure a good electrical contact between the sample and electrodes.

The impedance spectra were measured by a Solartron 1260 impedance analyzer equipped with a Solartron 1296 dielectric interface. An alternate-current sine signal with an amplitude of 1 V was sent to the sample, and its frequency ranged from 0.1 Hz to 10⁷ Hz. For electrical measurements, the pressure was loaded up to 23.2 GPa.

The in situ high-pressure angle-dispersive XRD measurements were conducted at beamline 4W2 of the Beijing Synchrotron Radiation Facility.^[28] The x-ray wavelength is 0.6199 Å. For better comparison with the measurements of the electrical transport properties, no pressure-transmitting medium was loaded. The distance between the sample and the detector, and the parameters of the detector, were calibrated with the CeO₂ standard. Bragg’s diffraction images were integrated using Fit2d software, yielding one-dimensional intensity versus diffraction angle 2θ patterns. The Rietveld refinements of crystal structures were performed using the program Materials Studio.

The XPS spectra (Figs. 1(a)–1(d)) reveal that the sample is composed of O, Y, and Zr elements. The C 1s peak comes from the adventitious carbon contamination in the XPS instrument. The specific high-resolution XPS spectra of the elements are shown in Figs. 1(a)–1(c). The peaks centered at 529.48 eV, 156.61 eV, and 181.52 eV correspond to O 1s for the O²⁺ state,^[29] Y 3d for the Y³⁺state, and Zr 3d for the Zr⁴⁺ state, respectively,^[30,31] indicating that the sample is composed of ZrO₂ and Y₂O₃. From the analysis in Table 1, the stoichiometric ratio of the sample is (ZrO₂)_0.618/(Y₂O₃)_0.382.

Fig. 1.

	Figure Option ViewDownloadNew Window
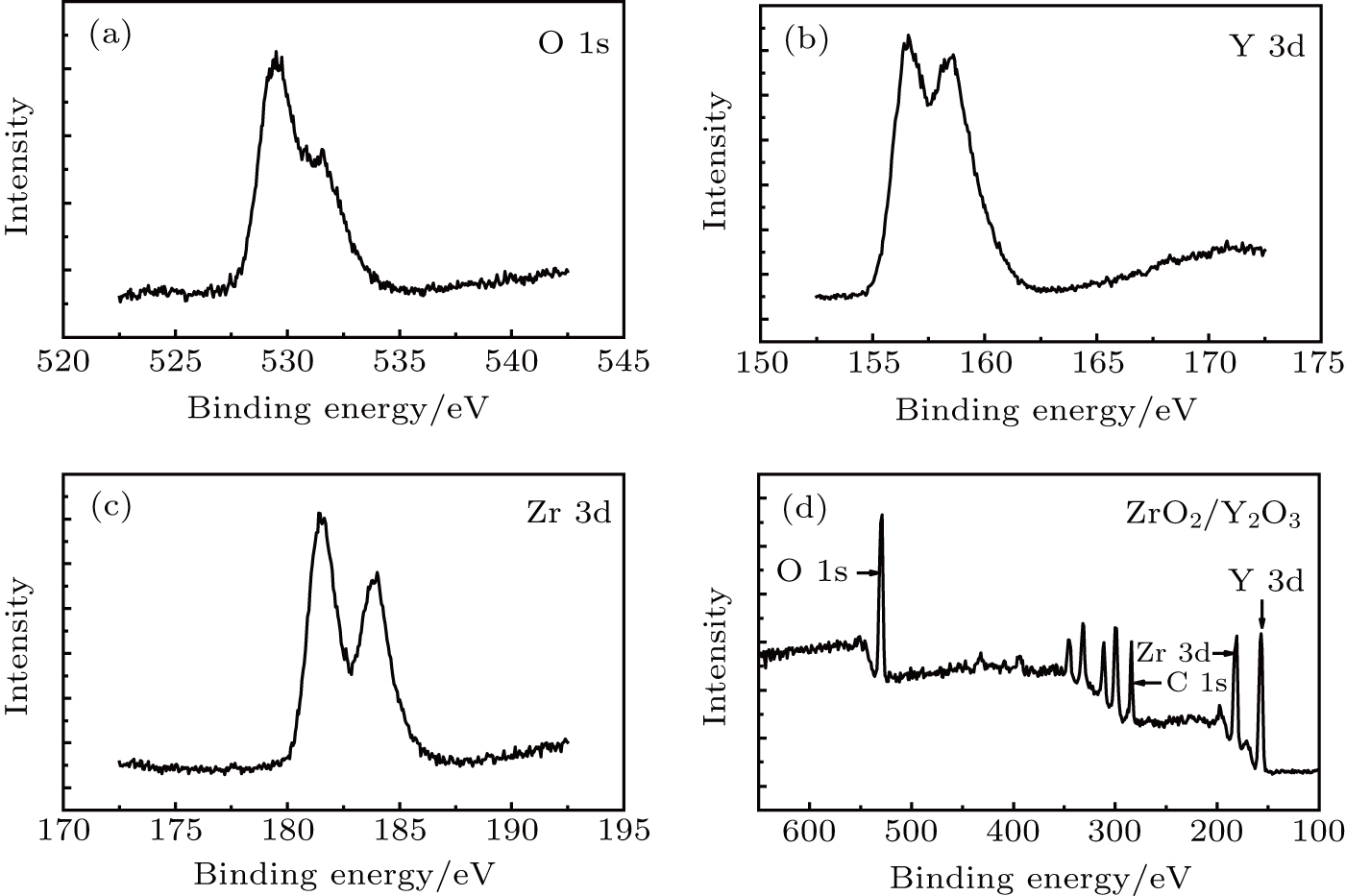	Fig. 1. XPS spectra of the ZrO2/Y2O3: (a) O region; (b) Y region; (c) Zr region; and (d) a survey spectrum.

Table 1.

Table 1.

Table 1. Parameters of Zr 3d, Y 3d, and O 1s in XPS spectra. BE stands for binding energy. . Name Start BE/eV Peak BE/eV End BE/eV Percentage/at.% Zr 3d 188.3 181.52 178.25 19.88 Y 3d 163 156.61 153.35 24.62 O 1s 536.5 529.48 525.8 55.5

Table 1. Parameters of Zr 3d, Y 3d, and O 1s in XPS spectra. BE stands for binding energy. .

Figure 2 shows the XRD spectrum for the synthesized (ZrO₂)_0.618/(Y₂O₃)_0.382 sample. All the diffraction peaks can be indexed as the cubic structure in space group Fm- , and the lattice constant is a = 5.2044 Å. The narrow and strong diffraction peaks suggest that the sample is well crystallized.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. XRD pattern of the synthesized sample.

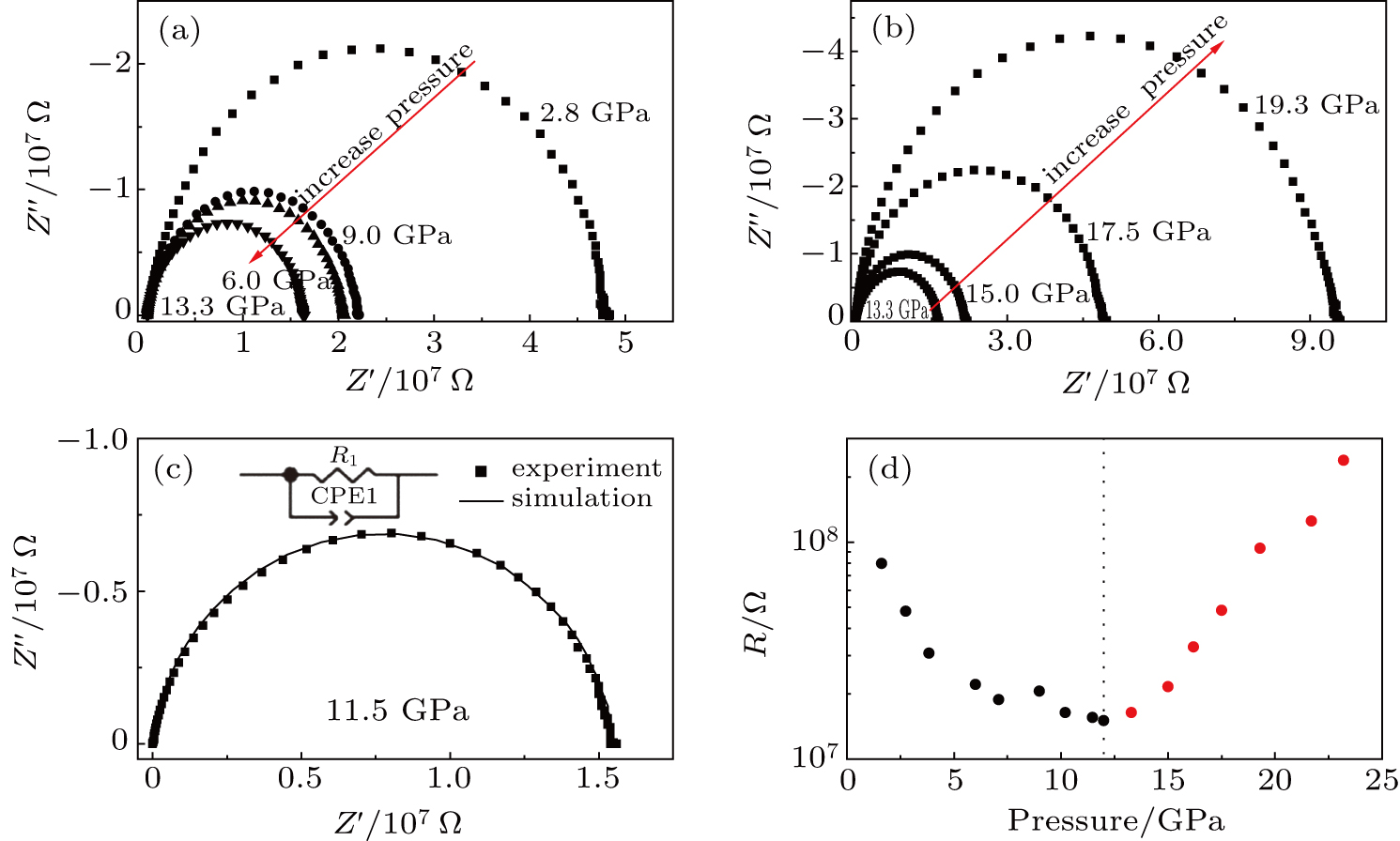
The impedance spectra of ZrO₂/Y₂O₃ solid solutions under high pressures are shown in Figs. 3(a)–3(d). Although the sample is polycrystalline, only one semicircle can be observed in the spectra, indicating that the grain and grain boundary of the sample have the same response to the alternate-current signal, and therefore they have the same impact on the electrical transport properties; otherwise, two semicircles should be seen. This behavior can be considered as a positive result for practical applications.

Since the difference between the grain and grain boundary is barely distinguishable, the equivalent circuit model used for further quantitatively analyzing the impedance spectra can be simplified as shown in Fig. 3(c), in which resistor R and constant-phase elements represent the total resistance and capacitance of grains and grain boundaries, respectively. Their parallel arrangement can describe the frequency response to the alternate-current signal. With the equivalent model, the total resistance R can be fitted at different pressures. The pressure dependence of R is shown in Fig. 3(d). It can be found that the pressure-dependent resistance shows two opposite change tendencies. Below 13.3 GPa, the resistance decreases as the pressure increases; but above 13.3 GPa, it increases sharply.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (a) and (b) Impedance spectra of ZrO2/Y2O3 under high pressures. (c) Fitting result for the impedance spectrum at 11.5 GPa. The fitting error is less than 5%. (d) Pressure dependence of bulk resistance of ZrO2/Y2O3. The black and red lines are guidance for the eyes.

Generally, the most possible reason for the abrupt change in resistance under high pressure is the pressure-induced structural phase transition or metallization.^[32,33] However, the pressure-induced metallization should be excluded from our case because the resistance value still remains at a high level ( ) in the whole experimental pressure region. Thus, the potential pressure-induced structural phase transition in ZrO₂/Y₂O₃ solid solutions is a primary issue that we need to consider in our study, and could be helpful for revealing the mechanism concealed behind the anomalous variation of the electrical transport properties of ZrO₂/Y₂O₃ under high pressure.

High-pressure XRD measurements are taken for ZrO₂/Y₂O₃ solid solutions up to 25.7 GPa. Selected representative spectra are shown in Fig. 4. It can be seen that all the diffraction peaks shift toward higher 2θ values and exhibit some broadened features due to the evolved nonhydrostatic conditions at high pressures. Except the shifts and broadening, no other obvious changes can be found in the diffraction peaks, suggesting that the crystal symmetry of ZrO₂/Y₂O₃ is stable within the pressure region we have studied. From the patterns of XRD spectra, we cannot see any evidence that the structure phase transition occurs in ZrO₂/Y₂O₃ at high pressures.

Fig. 4.

	Figure Option ViewDownloadNew Window
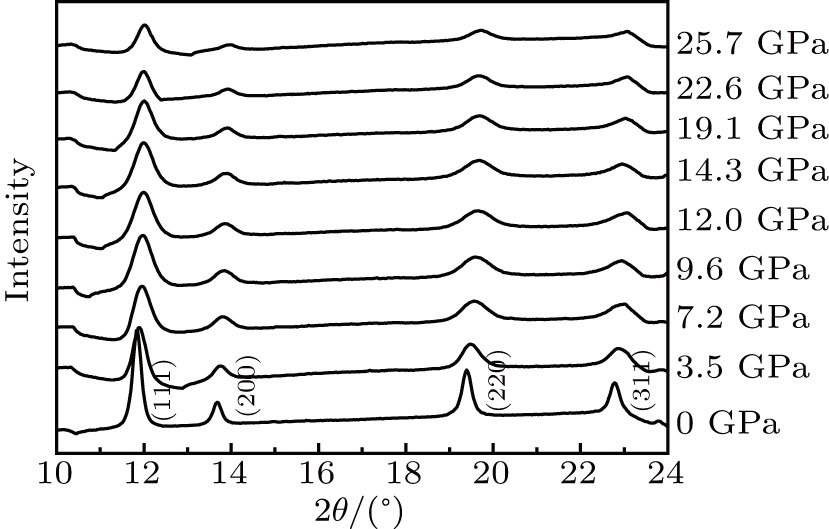	Fig. 4. Representative angle dispersive XRD patterns of ZrO2/Y2O3 at various pressures, with an incident wavelength λ = 0.6199 Å.

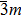
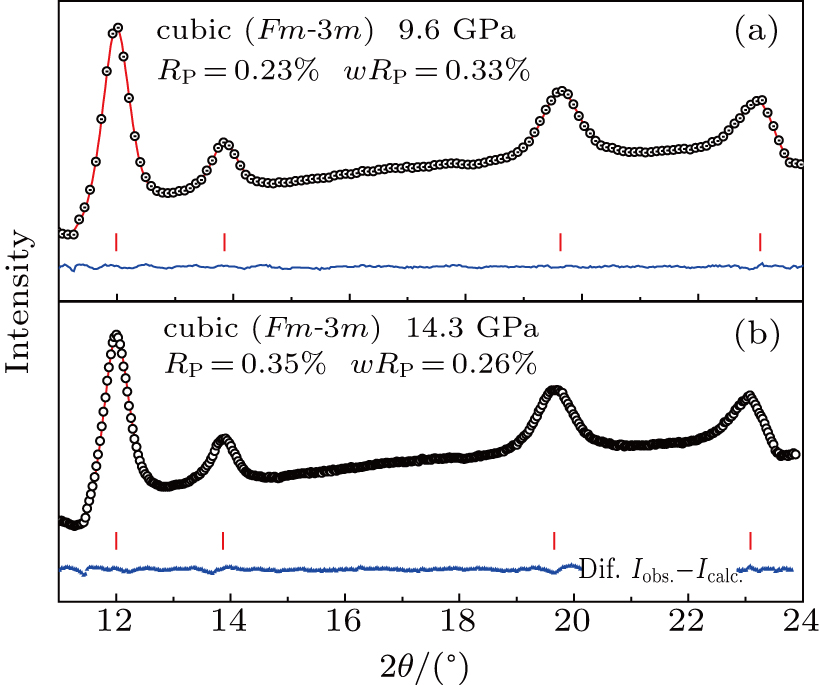By using the Rietveld fitting method, we analyze the XRD spectra carefully, and obtain the pressure-dependent lattice parameters and the equation of state. Figures 5(a) and 5(b) show the Rietveld refinement results for ZrO₂/Y₂O₃ in the cubic phase (Fm- ) at 9.6 GPa with R_p = 0.23%, wR_p = 0.33%, and at 14.3 GPa with R_p = 0.35%, wR_p) = 0.26%, respectively. They fit well with the experimental XRD spectra.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Representative Rietveld refinement results for XRD spectra of ZrO2/Y2O3 at (a) 9.6 GPa and (b) 14.3 GPa with an incident wavelength λ = 0.6199 Å.

The pressure-dependent d values of crystal planes (111), (200), (220), and (311) are drawn in Fig. 6. As pressure increases, the d values decrease correspondingly, indicating that the crystal structure becomes more compact. It can be clearly seen that the d values decrease with two different trends before and after 13.1 GPa. The pressure point in Fig. 3(d) happens to be where the total resistance changes abnormally. Pure ZrO₂ has been confirmed to have a pressure-induced phase transition from the monoclinic baddeleyite phase to the orthorhombic phase at approximately 10 GPa, with obvious appearance and disappearance of some diffraction peaks in XRD spectra;^[34] however, in our experiment, such behavior is not found. It is suggested that an isostructural phase transition in ZrO₂/Y₂O₃ solid solution should be responsible for the abnormal change in resistance.

Fig. 6.

	Figure Option ViewDownloadNew Window
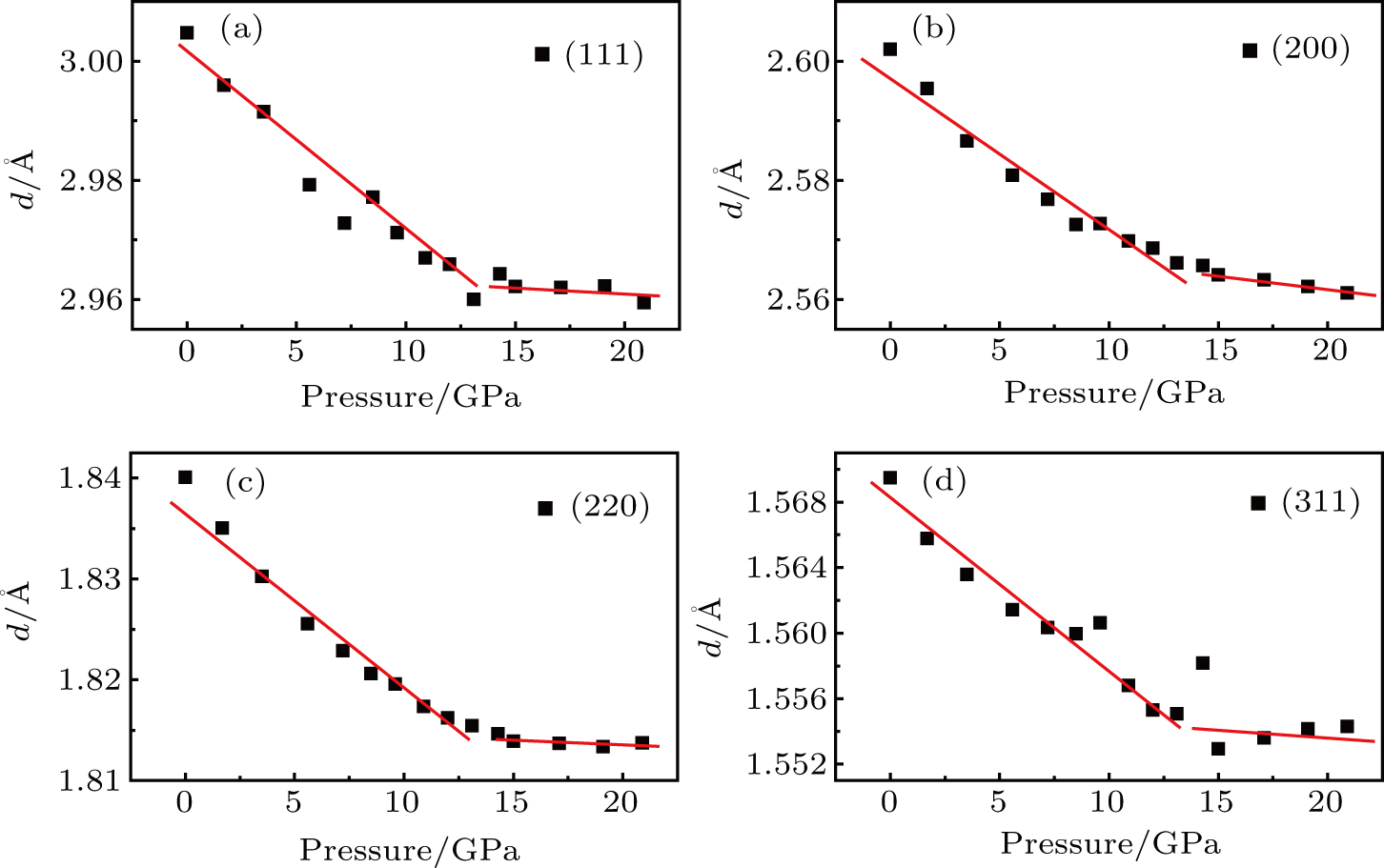	Fig. 6. Pressure dependence of different interplanar spacings: (a) (111), (b) (200), (c) (220), and (d) (311).

The pressure dependence of lattice constants and unit cell volume of ZrO₂/Y₂O₃ can be obtained from the Rietveld fitting results, as shown in Figs. 7(a) and 7(b). It can be seen that the pressure-induced isostructural phase transition is reversible, and no obvious hysteresis is found during decompression. The pressure-dependent unit cell volume is fitted with the Birch–Murnaghan equation of state^[35,36]

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. (a) and (b) Pressure dependence of the lattice constants and the unit cell volume of the cubic ZrO2/Y2O3. (c) and (d) Isothermal compression curves of ZrO2/Y2O3 at ambient temperature in two different pressure stages. The red line is a second-order Birch–Murnaghan fit to the experimental data.

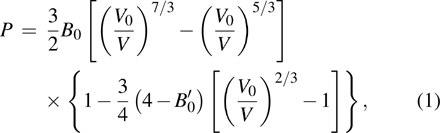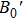
According to the method of least squares,^[36] we calculate the standard error values of B₀ in the two pressure stages. The results are shown in Table 2. Although the standard errors are relatively large, the big difference between B₀ values below and above 13.1 GPa is reliable enough to support the conclusion that a pressure-induced isostructural phase transition occurs in the ZrO₂/Y₂O₃ solid solution.

Table 2.

Table 2.

Table 2. B0 in two different pressure ranges. . Pressure stage/GPa B0/GPa below 13.1 125.2(5.6) 4.0 (fixed) above 13.1 290.3(21.3) 4.0 (fixed)

Table 2. B0 in two different pressure ranges. .

In summary, by combing in situ impedance and XRD measurements, we have studied the electrical transport and structural properties of the Y₂O₃-stabilized ZrO₂ solid solution under a high pressure up to 23.2 GPa. The pressure dependence of resistance reveals one potential and unknown change in Y₂O₃/ZrO₂ at 13.3 GPa, which had not been found before. The XRD measurement and Rietveld refinement further confirm that the abnormal change in resistance actually results from the pressure-induced isostructural phase transition in the Y₂O₃/ZrO₂ solid solution. By fitting the volume data with the Birch–Murnaghan equation of state, it is also found that the bulk modulus B₀ of the Y₂O₃/ZrO₂ solid solution increases by 131.9% from 125.2 GPa to 290.3 GPa due to the isostructural phase transition. This study may help deepen our knowledge for future applications of ZrO₂ solid solution-based devices under extreme conditions.