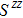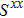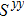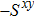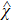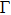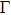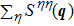† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11674158 and 11774152) and the National Key Projects for Research and Development of China (Grant No. 2016YFA0300401). W. Wang was also supported by the Program B for Outstanding PhD Candidate of Nanjing University.
We study various particle–hole excitations and possible superconducting pairings mediated by these fluctuations in doped α-RuCl3 by using multi-band Hubbard model with all t2g orbitals. By performing a random-phase-approximation (RPA) analysis, we find that among all particle–hole excitations, the jeff = 1/2 pseudospin fluctuations are dominant, suggesting the robustness of jeff = 1/2 picture even in the doped systems. We also find that the most favorable superconducting state has a d-wave pairing symmetry.
The doped Mott insulators[1–6] have been subject to extensive investigations because they contain plentiful phases, such as spin-density wave (SDW), pseudogaps, and superconductivity. In parent compounds, the charge insulation of most Mott insulators raises solely from the Coulomb interaction. However, recently a new family of Mott insulator, in which the charge insulation is resulted from the cooperative interplay between spin–orbit coupling (SOC) and electron correlation, has been proposed, such as Sr2IrO4,[7,8] Na2IrO3,[9–11] and α-RuCl3.[12–14] In these Mott insulators, the electron configuration for the active ions is d5, such as 5d5 of Ir4+ in iridates and 4d5 of Ru3+ in ruthenium. Within the octahedral crystal field, the d orbitals are split into a two-fold eg manifold and a three-fold t2g manifold with an effective leff = 1 orbital moment. The latter are further divided into a fully filled jeff = 3/2 band and a half-filed jeff = 1/2 narrow band by strong SOC. Then the jeff = 1/2 band only needs a moderate electronic correlation to open a Mott gap. Thus these Mott insulators are usually referred to as spin–orbit assisted Mott insulators.
The novel physics of these jeff = 1/2 Mott materials in different lattices has been reported both experimentally and theoretically. For the square lattice, a canted antiferromagnetic structure has been found in Sr2IrO4,[15–17] which is isostructural to La2CuO4, a parent compound for cuprate superconductors. Similar to the doped cuprate Mott insulator, pseudogap, Fermi arc,[18–21] and superconductivity[22–26] are also addressed in doped Sr2IrO4. For the honeycomb lattice, an intriguing physics is that the Kitaev interactions underlying the celebrated Kitaev model,[27] whose ground state is exactly a Z2 spin liquid with Majorana fermion excitations, can be realized.[28] In this aspect, the honeycomb-lattice material α-RuCl3 has recently attracted much attention.[12–14,29,30] Although the ground state of α-RuCl3 has a long-range zigzag magnetic order, a broad continuous spectrum in inelastic neutron scattering has been observed[12–14] and the magnetic order can be fully suppressed by either an in-plane magnetic field[31–33] or pressure.[34–36] There is accumulating evidence that the field-induced disordered state is a promising candidate as a quantum spin liquid.[31–33] For doped systems, the jeff = 1/2 Mott materials with honeycomb lattice also exhibit many exotic physics, such as unconventional superconductivity[37–41] and unique charge dynamics.[42–49]
In this paper, based on the multi-band Hubbard model including all t2g orbitals, we investigate various particle–hole (PH) excitations and possible superconducting pairings mediated by these fluctuations in the doped systems with the random-phase-approximation (RPA) method. We find that the jeff = 1/2 pseudospin fluctuations dominate over the fluctuations from other particle–hole excitations, suggesting the robustness of the jeff = 1/2 picture even in the doped systems, and the most favorable superconducting state mediated by the pseudospin fluctuations has a d-wave pairing symmetry.
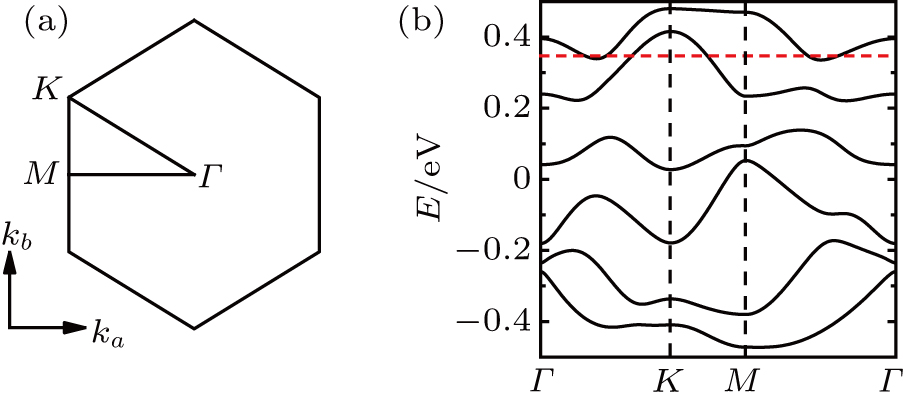
The low-energy physics of α-RuCl3 is dominated by the t2g orbitals due to the 4d5 configuration of Ru3+ and the octahedral crystal field, so our calculations are based on the t2g three-orbital model,[30] which is derived through fitting the band structure from the density-functional theory (DFT). The three-orbital Hamiltonian is given as
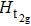
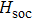
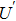
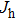
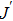
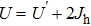
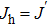
Based on the scenario that the pairing interaction arises from the PH fluctuations, we can calculate the effective electron–electron interactions using the RPA. However, as a result of the effect of the SOC, the effective particle–particle interaction cannot be simply divided into bubble and ladder diagrams as is the case with SU(2) symmetry.[50] Thus, to include the SOC in the RPA approach, we use the Hugenholtz diagrams in our calculations.[20] In this method, the susceptibilities from the PH excitations are given by
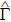

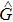
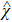
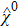
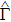
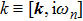
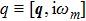
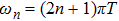
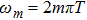
The effective interaction in the particle–particle channel is given by[20]
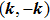
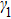
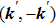
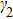
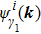
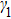
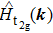
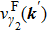
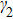
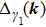
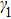
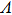
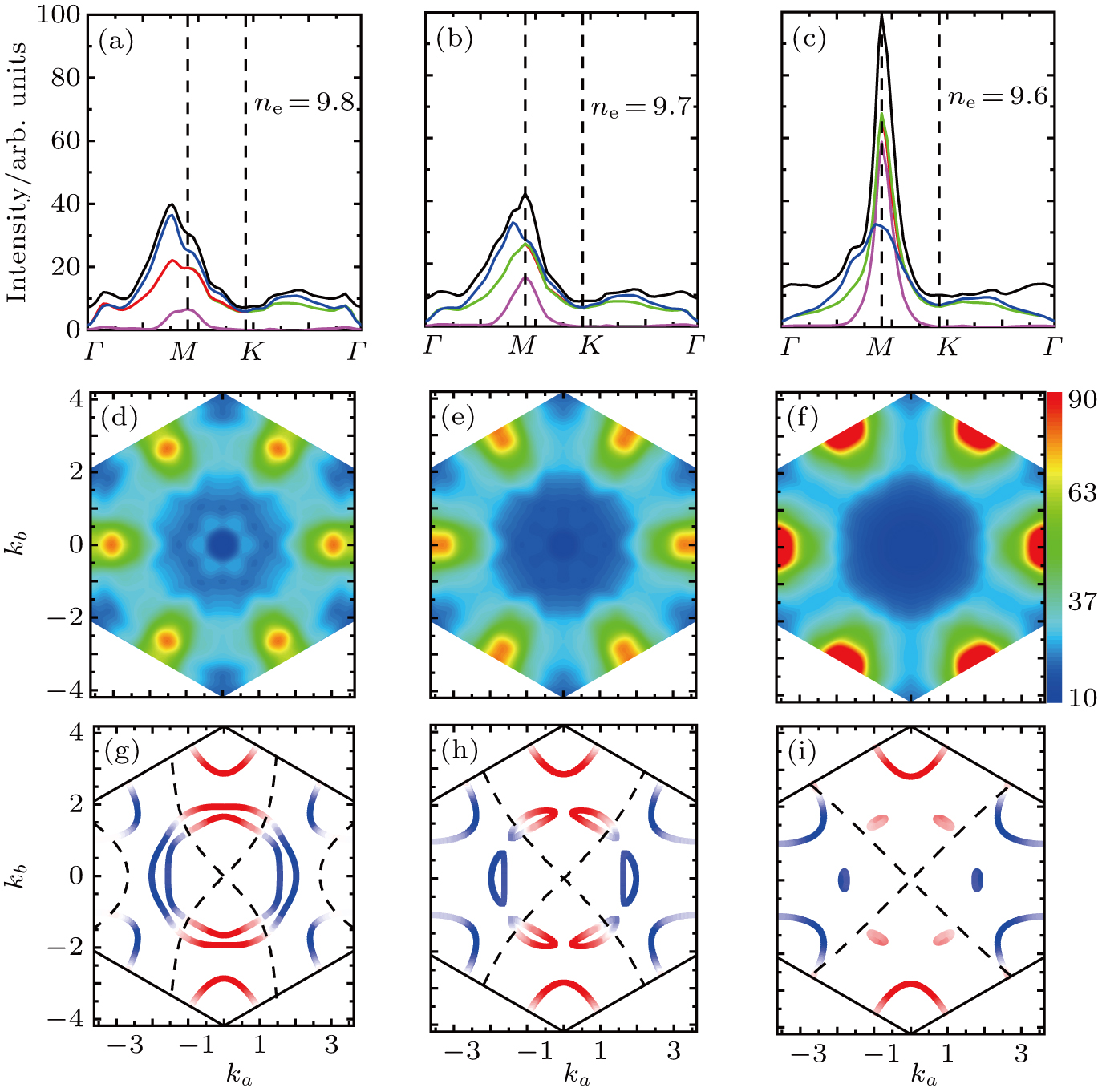
Let us first study the main properties of the PH excitations in the hole doped system. To find the dominant PH excitations, we classify various PH channels according to the total angular momentum of a PH pair. Generally, the susceptibility can be written in terms of 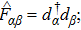
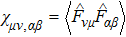
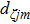
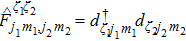
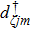

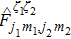
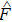
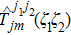
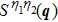
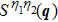
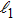
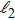
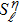
In Figs. 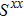
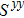
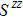
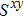
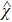
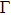
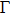
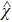
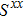
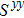
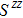
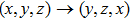
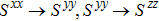
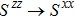
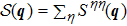
We then study the properties of superconducting pairing by solving Eq. (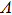
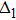
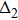
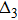
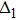
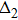
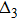
Thus, the pairing gap functions for ne=9.7 and ne=9.6 have a dominant d-wave superconducting pairing along the nearest-neighbor sites, which can also been seen from the sign and nodes of the gap functions shown in Figs.
Next, we turn to the electron doped systems. In Fig. 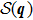
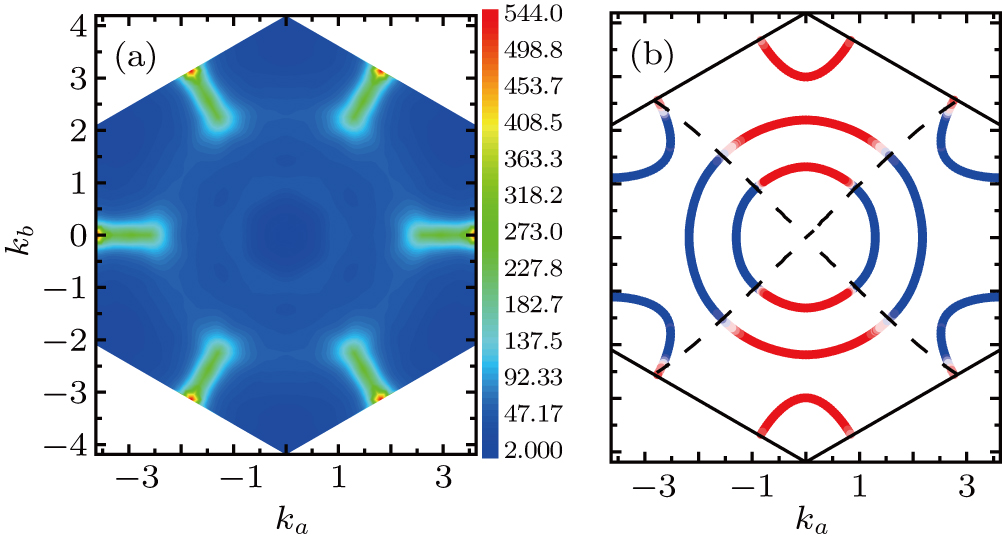 | Fig. 3. (a) Static susceptibility and (b) superconducting gap function for electron doped system with ne=10.1. |
Thus, we find that the d-wave pairing mediated by the jeff = 1/2 pseudospin fluctuations is the most favorable superconducting pairing symmetry for both hole and electron dopings. The explicit forms of the d-wave gap functions we obtained here are expected to be helpful for identifying the pairing symmetry if superconductivity in α-RuCl3 is realized experimentally in the future.
In summary, based on the multi-band Hubbard model with all t2g orbitals and by use of the random-phase approximation, we have investigated various particle–hole excitations and possible superconducting pairing symmetry in doped α-RuCl3, in which the strong spin–orbit coupling and electron correlations cause an effective total angular momentum jeff = 1/2 Mott insulator. We find that the jeff = 1/2 pseudospin fluctuation dominates over other fluctuations in a large doping range, which suggests that the jeff = 1/2 picture is still robust in the doped systems. Through projecting particle–particle interaction onto Fermi surfaces, we find that the d-wave pairing is the most favorable superconducting pairing symmetry in both the hole- and electron-doped systems.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] |