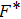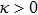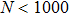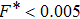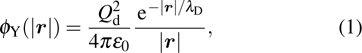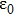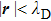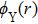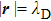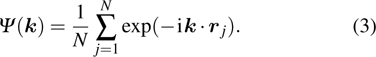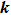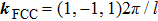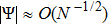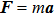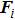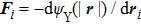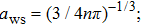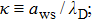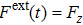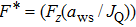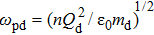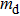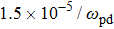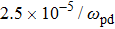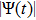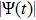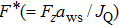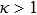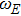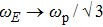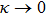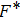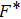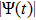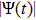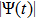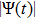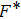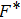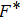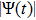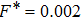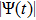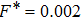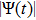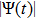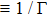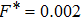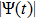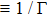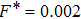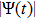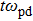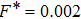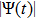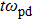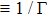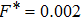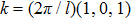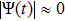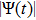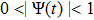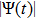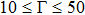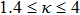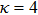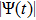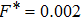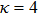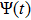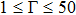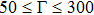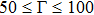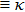Crystalline order and disorder in dusty plasmas investigated by nonequilibrium molecular dynamics simulations
1. IntroductionExploration of the structural properties of various materials is an exceptional task in material sciences and has application in dusty plasmas. Various developments in this field have been attained over the last two decades using a variety of experimental, theoretical, and computational approaches. Plasma is generally considered as the most disordered state of matter. Dusty plasma can be composed of dust particles of different sizes that are embedded in the plasma system. These dust particles establish regular patterns in the dusty plasma system. Plasma and dust charged particles are the two omnipresent ingredients of the universe. The interplay between these two has opened up a new and fascinating research area, besides the research of the Bose–Einstein condensate. Precise measurements for the structural properties of dusty plasmas are necessary to optimize the design of these devices because structural analysis defines the phase state of the system.[1, 2] Dusty plasma is an entirely new material, whose crystalline structure is so outstandingly observed that it could be a valuable tool for studying physical processes in condensed matter physics. Theoretical, simulation, and experimental techniques are helpful to investigate the structural behavior of these materials. The accurate numerical calculation of the structural behavior of complex systems is an important investigation in material science and its allied branches. Currently, several thermophysics groups have investigated the order–disorder structures (OD-structures) data that are closely associated to the experimental setup and these data verify the phase states of these complex systems. Worldwide acceptable data of particle crystalline structures are also necessary for an optimized design of processes and for novel methods in science and technology (thermoelectric and photoelectric devices). In particular, the provision of precise information for the static and dynamical characteristics is demanded.
Nonideal complex systems (NICSs), which are also referred as complex dusty plasmas, have unlocked a completely new line of research in applied plasma and condensed matter physics and have led to the development of novel technologies. Experimentally, dusty plasmas are created by dispersing micron-sized particles into gas discharges.[3, 4] The typical direct current (dc) glow discharge and radio-frequency (rf) sources are used to investigate various properties of dusty plasma systems. The dust particles are exposed to electron and ion currents from the discharge plasma, and a dynamic equilibrium is rapidly reached. Their electric charge can be in the order of ∼103–104 electron charges, depending on the diameter of the particles. The high charge of the particles gives rise to a strong electrostatic repulsion between them, which may lead to crystallization in a confined system.[5] In an experimental device, the particles interact with their environment via several forces. Theoretically, dusty plasmas are treated as many body systems in the extreme limits of both weak interaction and very strong interaction. For the weak interactions, one is faced with a gaseous system, or Vlasov plasma, where correlation effects can be treated perturbatively. Sophisticated theoretical approaches such as the random phase approximation method[6] based on the linear response theory can be used to calculate the dynamical structural properties when the correlation effects are negligible. In the case of very strong interactions, the systems crystallize, the particles are completely localized and phonons are the principal excitations. For these conditions, lattice-summation techniques serve as a solid basis to obtain information on a dusty plasma system.[7]
In the last few decades, the practical importance in dusty plasmas research in ionized gas containing nanometer to millimeter sized particles of condensed matter has been realized. The large values of charge cause frequent and strong interparticle interactions as compared to the small value of charged particles. Dust–plasma interactions are also important in the industrial laboratory. For example, the nuisance and hazards related to dust charging in mill, granaries and mines have been known for a long time. Also, plasma processing (xerography) is now used in the semiconductor manufacturing industry. In addition, dust particles have been effectively used in electrostatic precipitation (air cleaning), separation and spraying (sizing, recycling, etc.), as well as in the sterilization and electrophoresis of biological material.[8, 9] The condensation and transport of fine dust particles in these high-density and low-temperature plasmas, leading to product yield loss, are the significant problems in this multibillion dollar industry, and it is expected to become more important as the feature sizes decrease in the future. Moreover, gaseous–liquid–solid phase transition and structure are under consideration because of the analogy with condensed matter (surfactants, colloidal suspensions, polymers, two-dimensional plasma, etc).[10–12] Here, matter is in the strongly coupled regime when the interaction energy of neighboring particles is larger than the energy of a particle's random motion. This is true for liquids and solids in which neutral atoms are densely packed. In Yukawa (screened Columbic) systems (Debye screening strength
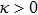 ), it has been shown theoretically that the exact OD structures (long-range order) cannot exist at finite temperatures
), it has been shown theoretically that the exact OD structures (long-range order) cannot exist at finite temperatures
 .[13] Nonetheless, crystal-like, fluid-like, and effects of mass-to-charge variation behaviors have been observed in different complex systems and pronounced changes of certain characteristics have been detected in the transition region between these two phases in both simulations[12–20] and experiments.[21–25] To understand these phases, the liquid and solid states of strongly coupled complex dusty plasmas (SCCDPs) are of considerable interest. The Coulomb (plasma) coupling parameter (Γ) associated with temperature (=1/Γ) explains the corresponding states in SCCDPs. Therefore, the precise value of Γillustrates the nonideal to crystal structure states (OD-structures) and the ordered state is also the so-called plasma crystal state. The order structures are caused by the combined effective Coulomb interactions of dust particles and the disorder state is formed by the random thermal motion which leads to different positions in between solid crystal phase and liquids or gaseous phase.[26] Plasma crystals are examples of dusty plasma systems in the strongly coupled region. This entirely new material (plasma crystal), whose crystalline structure is so strikingly observed by laser light scattering, could be a valuable tool for studying physical processes in condensed matter, such as melting, annealing, and lattice defects. The dust particles in plasma crystals are negatively charged by the surrounding plasma and they carry thousands of elementary charges. Therefore, the regime of strong coupling is formed at room temperature whereas ions crystallize only at 10−3 K.[27, 28] The plasma crystal is formed by dust particles and these particles adopt BCC-like or HCP and FCC as well as string like structures in two-dimensional (2D) or three-dimensional (3D) multilayer systems.[29] Another promising area of research is to investigate the dynamics of dusty plasma under a magnetic field.[30, 31] The structure of magnetized dusty plasmas can be computed through numerical methods.[32] An inclusive development of the presence of 3D particle crystalline structures has been studied but the investigation of OD-structures corresponding to Yukawa potential energy (PE) of SCCDPs is still an alternative goal of researchers through novel methods.[12–17, 32] This is imitated by the enduring discussion on the crystalline OD-structures presence and basic phenomena of Yukawa PE in SCCDPs.
.[13] Nonetheless, crystal-like, fluid-like, and effects of mass-to-charge variation behaviors have been observed in different complex systems and pronounced changes of certain characteristics have been detected in the transition region between these two phases in both simulations[12–20] and experiments.[21–25] To understand these phases, the liquid and solid states of strongly coupled complex dusty plasmas (SCCDPs) are of considerable interest. The Coulomb (plasma) coupling parameter (Γ) associated with temperature (=1/Γ) explains the corresponding states in SCCDPs. Therefore, the precise value of Γillustrates the nonideal to crystal structure states (OD-structures) and the ordered state is also the so-called plasma crystal state. The order structures are caused by the combined effective Coulomb interactions of dust particles and the disorder state is formed by the random thermal motion which leads to different positions in between solid crystal phase and liquids or gaseous phase.[26] Plasma crystals are examples of dusty plasma systems in the strongly coupled region. This entirely new material (plasma crystal), whose crystalline structure is so strikingly observed by laser light scattering, could be a valuable tool for studying physical processes in condensed matter, such as melting, annealing, and lattice defects. The dust particles in plasma crystals are negatively charged by the surrounding plasma and they carry thousands of elementary charges. Therefore, the regime of strong coupling is formed at room temperature whereas ions crystallize only at 10−3 K.[27, 28] The plasma crystal is formed by dust particles and these particles adopt BCC-like or HCP and FCC as well as string like structures in two-dimensional (2D) or three-dimensional (3D) multilayer systems.[29] Another promising area of research is to investigate the dynamics of dusty plasma under a magnetic field.[30, 31] The structure of magnetized dusty plasmas can be computed through numerical methods.[32] An inclusive development of the presence of 3D particle crystalline structures has been studied but the investigation of OD-structures corresponding to Yukawa potential energy (PE) of SCCDPs is still an alternative goal of researchers through novel methods.[12–17, 32] This is imitated by the enduring discussion on the crystalline OD-structures presence and basic phenomena of Yukawa PE in SCCDPs.
The basic objective of this work is to investigate the particle crystalline structures (lattice correlation ψ (t)) and potential energies of NICSs by employing the same technique as introduced by Shahzad and He.[26] This numerical technique has already been employed for dynamical coefficients of simple and dense fluids,[33] rheological problems of Yukawa systems,[34, 35] semiconductor systems,[36] and one-component Coulomb plasma (OCCP).[37] Therefore, in the limit of zero external force field strength, this technique is regarded as the best computational tool; as reported in Ref. [33] and the references herein. Moreover, the presented technique has been used for suitable plasma states (Γ, κ) with small system sizes. It has also been used to check how to compute the long range crystalline order in SCCDPs at constant force field with body-centered cubic (BCC) crystal structure. This BCC lattice structure has been confirmed experimentally.[29] A detailed study has been reported by the presented authors on 3D OD-structures at larger system sizes of SCCDPs [OD] for face-centered cubic (FCC) crystal structure;[13] however, this paper is limited for the small system sizes (
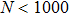 ) at normalized force field strength
) at normalized force field strength
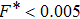 with BCC structure. The effect of foreign force on ψ (t) is another imperative job at nearly equilibrium conditions. In the second section, the Fourier transformation along with the refined Evans's algorithm for homogenous nonequilibrium molecular dynamics (HNEMD) technique is used to amount the BCC crystalline structure for 3D Yukawa systems. In the third and fourth sections, the outcomes of OD-structures of NICSs through an improved HNEMD approach are reported and compared to the prior numerical results. Finally, the work is summarized in the last section.
with BCC structure. The effect of foreign force on ψ (t) is another imperative job at nearly equilibrium conditions. In the second section, the Fourier transformation along with the refined Evans's algorithm for homogenous nonequilibrium molecular dynamics (HNEMD) technique is used to amount the BCC crystalline structure for 3D Yukawa systems. In the third and fourth sections, the outcomes of OD-structures of NICSs through an improved HNEMD approach are reported and compared to the prior numerical results. Finally, the work is summarized in the last section.
2. OD-structure model and HNEMD techniqueThe crystalline (particle lattice) structures and the correspondence potential energies can be measured with Green–Kubo relations (GKRs), which are basically used for uncharged particles and can be employed for the complex systems (dusty plasmas). The Yukawa potential model, which is screened Coulomb potential, is one of the most appropriate ways to describe charge particles having a interparticle potential, especially for laboratory dusty plasma[13, 26, 38, 39]
where
λ
D represents the Debye screening length,
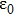
represents the permittivity of free space,
Q
d represents the charge on dust particle, and

represents the interparticle distance between two dust particles. For
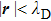
, the potential
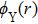
between particles is identical in a vacuum, whereas the effective dust particle is completely screen by its adjacent shield for

. For
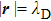
, the collective behavior of dust particles diminishes and only one-to-one Coulombic interaction exists between the dust particles. The correlation function gives the statistical correlation between the random variables, probable on the spatial or temporal position. These functions quantify how microscopic variables co-vary with one another on average across space and time. In our case, we discussed particles position–position correlation function (often called pair correlation or radial distribution function). In solids, the lattice correlation has defined the long-range crystalline alignment, additionally also delivers the nature and occurrence of a lattice structure for the systems. With the help of correlation functions, the extracted data from the experimental mechanism like neutron diffraction or x-ray scattering calculation for a specific crystalline material can be explained. Computer simulations can also be employed to investigate the dynamic and structure of the system. Computer experiments have been employed on numerous kinds of fluids, such as simple liquids, polymer, ionic system, alloys, colloidal suspensions, dusty plasmas, and so on.
[1–13, 32, 33] The characterization of crystalline structural formation in a complex system is not trivial and it is associated with an exact parameter of complex structure for order and disorder. For Yukawa liquids, dust particles are selected to be spherical with long range attractive forces. The HNEMD algorithm evaluates the long-range order of complex Yukawa liquids by letting the same edge length of simulation box via Eq. (
1). If the particles are in an ordered form (i.e., solid, liquid, or crystal state), then the state of matter leads toward the number density of material. So the local density is computed at point

as
[13]Therefore, the crystalline (particle lattice correlation) structure can be obtained by applying the Fourier transformation and equation (
2) turns over lattice correlation as
The computation of Eq. (
3) explains the existence of long-range alignment in complex dusty plasma systems. Here, the
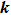
represents the reciprocal lattice vector of order–disorder states of the NICSs. The reciprocal lattice vectors for different crystal structures like simple cubic (SC), face-centered cubic (FCC), body-centered cubic (BCC) are

,

,
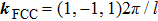
, respectively. In our case, we have employed BCC for investigating OD-structures of NICSs unlike our previous work,
[13] where we have employed the FCC crystal structure. At

, the system is in an ordered state and
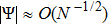
provides the system in disorder state.
[26] For the HNEMD case, the number of particles is chosen to be
N = 256, 500, 864 that allows a study of the effects of suitable small system size for the confirmation of our previous results.
[13, 26, 35, 39] The dust particles density is calculated as
n =
N/
V, where
V is the volume of the system and the computation evolution is obtained by solving equations of motion for a Yukawa system of
N particles.
[34] The motion of dust particles is based on Newton's second law of motion, formulated as
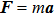
. The interaction force on a single particle
i is the sum of all forces exerted by all other particles on the particle, formulated as

but

. Further
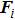
is computed by taking the negative derivative of the Yukawa potential given in Eq. (
1); i.e.,
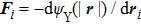
. These dust particles interact through the Yukawa pair potential and are bound in a computational box of volume
V. The current potential model has been used for the exploration of interaction energy and corresponding forces of repelling dust charged particles in numerous physical mechanisms.
[13, 26, 35, 39] In our case, two normalized criterion are important to describe the plasma states for the Yukawa potential mechanism: first is Coulomb coupling strength

) (

), in which

represents the Wigner–Seitz (WS) radius
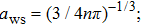
and second is Debye screening strength
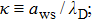
in the limit of

, the interactions reduce to the Coulomb interaction. An additional parameter is the normalized foreign force field strength
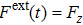
and its normalized value is
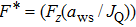
, where
J
Q is the heat energy current and is given in Refs. [
13], [
26], [
35], [
38], and [
40]. These parameters define the long range structural alignment of dusty plasma system. The dimensions of the simulation box are

, where
a
ws is the average separation between the nearest dust particles. The Ewald sums method with periodic boundary conditions (PBCs) is used to calculate the Yukawa potential energies and forces during each HNEMD simulation run. The PBCs and image conventions are used to remove the surface effects and HNEMD simulations are performed in a canonical ensemble (
NVT). Usually, the Gaussian thermostat is used to control the temperature of the Yukawa system. Furthermore, the classification of time scale for dusty plasma system is in terms of frequency, i.e., the inverse of plasma frequency
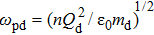
, where
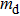
represents the dust particle mass and the time integration is performed using a fifth order predictor–corrector scheme with simulation time step of

that permits us to calculate the essential data at enough long time.
[35, 38, 39] The actual HNEMD computations are employed between
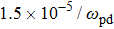
and
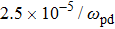
. Two to three separate HNEMD computation jobs have been exercised with randomly selected collections of the dust grains positions and finally we obtain the average of the simulation outcomes in order to minimize the statistical noise and to develop the statistics of the HNEMD outcomes. In this paper, the HNEMD scheme is employed for the particle lattice (Ψ(
t)) and the corresponding Yukawa PE of 3D strongly coupled (SC) NICSs over a wide range of Coulomb coupling of Γ= (10, 300) and
κ = (1.4, 4).
3. Computational results and discussionIn this section, the particle crystalline (long range) order
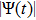 measurements are obtained by using the HNEMD scheme, Eq. (3) with BCC lattice structure, for 3D SC-NICSs. The particle OD-structures
measurements are obtained by using the HNEMD scheme, Eq. (3) with BCC lattice structure, for 3D SC-NICSs. The particle OD-structures
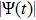 are compared here with appropriate plasma frequency (
are compared here with appropriate plasma frequency (
 ) normalization in the limit of a suitable steady state low value of scaled external force field
) normalization in the limit of a suitable steady state low value of scaled external force field
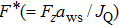 over a wide range of Coulomb couplings (
over a wide range of Coulomb couplings (
 ) and Debye screening strengths (
) and Debye screening strengths (
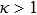 ). It has been shown that
). It has been shown that
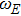 decreases with an increase of κ and
decreases with an increase of κ and
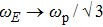 as
as
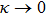 for the 3D case.[13, 15] We have computed the long range order to understand the varying structural behaviors under nearly equilibrium conditions for the SC-NICSs. The homogenous nonequilibrium Yukawa system is equilibrated by using Gaussian thermostat (α) in order to remove heat that is generated due to work done by normalized force field
for the 3D case.[13, 15] We have computed the long range order to understand the varying structural behaviors under nearly equilibrium conditions for the SC-NICSs. The homogenous nonequilibrium Yukawa system is equilibrated by using Gaussian thermostat (α) in order to remove heat that is generated due to work done by normalized force field
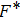 and details of α have been reported in Refs. [33]–[39]. The presented enhanced HNEMD technique facilitates to calculate all the feasible ranges of plasma parameters (Γ, κ) at constant scaled external force field
and details of α have been reported in Refs. [33]–[39]. The presented enhanced HNEMD technique facilitates to calculate all the feasible ranges of plasma parameters (Γ, κ) at constant scaled external force field
 . For HNEMD outcomes reported here, we have checked and varied the following parameters: system size (N), scaled external force field (
. For HNEMD outcomes reported here, we have checked and varied the following parameters: system size (N), scaled external force field (
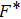 ), thermostat (α), simulations total run time (t), simulation step size (
), thermostat (α), simulations total run time (t), simulation step size (
 ), Debye screening (κ), and Coulomb coupling (system temperature
), Debye screening (κ), and Coulomb coupling (system temperature
 ) for the investigation of plasma crystalline OD-structures
) for the investigation of plasma crystalline OD-structures
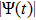 and the corresponding Yukawa PE. It is interesting that the present alternative HNMED scheme gives reasonable
and the corresponding Yukawa PE. It is interesting that the present alternative HNMED scheme gives reasonable
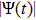 measurements with small system size and BCC arrangements over a complete range of mentioned plasma states (Γ,
measurements with small system size and BCC arrangements over a complete range of mentioned plasma states (Γ,
 ) as compared to the earlier used numerical scheme with higher N and FCC arrangements and also better than those used the previous methods based on different numerical schemes[13, 26, 35, 39] for the SC-NICSs. The outcomes computed are compared and argued with the previous numerical outcomes, theoretical and experimental measurements at almost the similar sets of plasma state points (Γ, κ) of SC-NICSs in the gas-like, liquid-like, and crystal-like phases. It is remarkable that measurable accurate outcomes have been computed for the
) as compared to the earlier used numerical scheme with higher N and FCC arrangements and also better than those used the previous methods based on different numerical schemes[13, 26, 35, 39] for the SC-NICSs. The outcomes computed are compared and argued with the previous numerical outcomes, theoretical and experimental measurements at almost the similar sets of plasma state points (Γ, κ) of SC-NICSs in the gas-like, liquid-like, and crystal-like phases. It is remarkable that measurable accurate outcomes have been computed for the
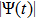 of 3D SC-NICSs and Yukawa PE from an extended HNEMD scheme at unlike arrangements of crystal structure of FCC, and taking a smaller number of independent particles N than used former, to show that our new numerical data of
of 3D SC-NICSs and Yukawa PE from an extended HNEMD scheme at unlike arrangements of crystal structure of FCC, and taking a smaller number of independent particles N than used former, to show that our new numerical data of
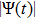 and PE are well matched with the previous known accessible results.
and PE are well matched with the previous known accessible results.
Our investigations have usually given acceptable conformity with previous numerical results of 3D SC-NICSs at a very low scaled external force strength of
 . This
. This
 (= 0.002) is a practical constant force field for the examination of nearly equilibrium (steady state) values of plasma crystalline structure
(= 0.002) is a practical constant force field for the examination of nearly equilibrium (steady state) values of plasma crystalline structure
 and Yukawa PE, where the signal to noise ratio is suitable for all the plasma states (Γ, κ). We have tested the force field strengths lower and higher than
and Yukawa PE, where the signal to noise ratio is suitable for all the plasma states (Γ, κ). We have tested the force field strengths lower and higher than
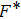 (= 0.002) for different varying plasma states with BCC lattice structure arrangements. The present authors have already reported that the force field
(= 0.002) for different varying plasma states with BCC lattice structure arrangements. The present authors have already reported that the force field
 lower than (0.001) and higher than (0.1) provides comparatively noisy measurements.[13] Therefore, it is noted that different sequences of varying force field
lower than (0.001) and higher than (0.1) provides comparatively noisy measurements.[13] Therefore, it is noted that different sequences of varying force field
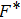 have no significant effects on the particle lattice structures
have no significant effects on the particle lattice structures
 with BCC arrangements, especially, low sequences of
with BCC arrangements, especially, low sequences of
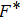 . It is remarkable that the HNEMD outcomes of dusty plasma crystalline structure
. It is remarkable that the HNEMD outcomes of dusty plasma crystalline structure
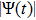 show excellent behaviors and well explain the dusty plasma OD-structures in different phases (nonideal gas, liquid, and crystalline) with BCC arrangements at constant
show excellent behaviors and well explain the dusty plasma OD-structures in different phases (nonideal gas, liquid, and crystalline) with BCC arrangements at constant
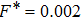 .
.
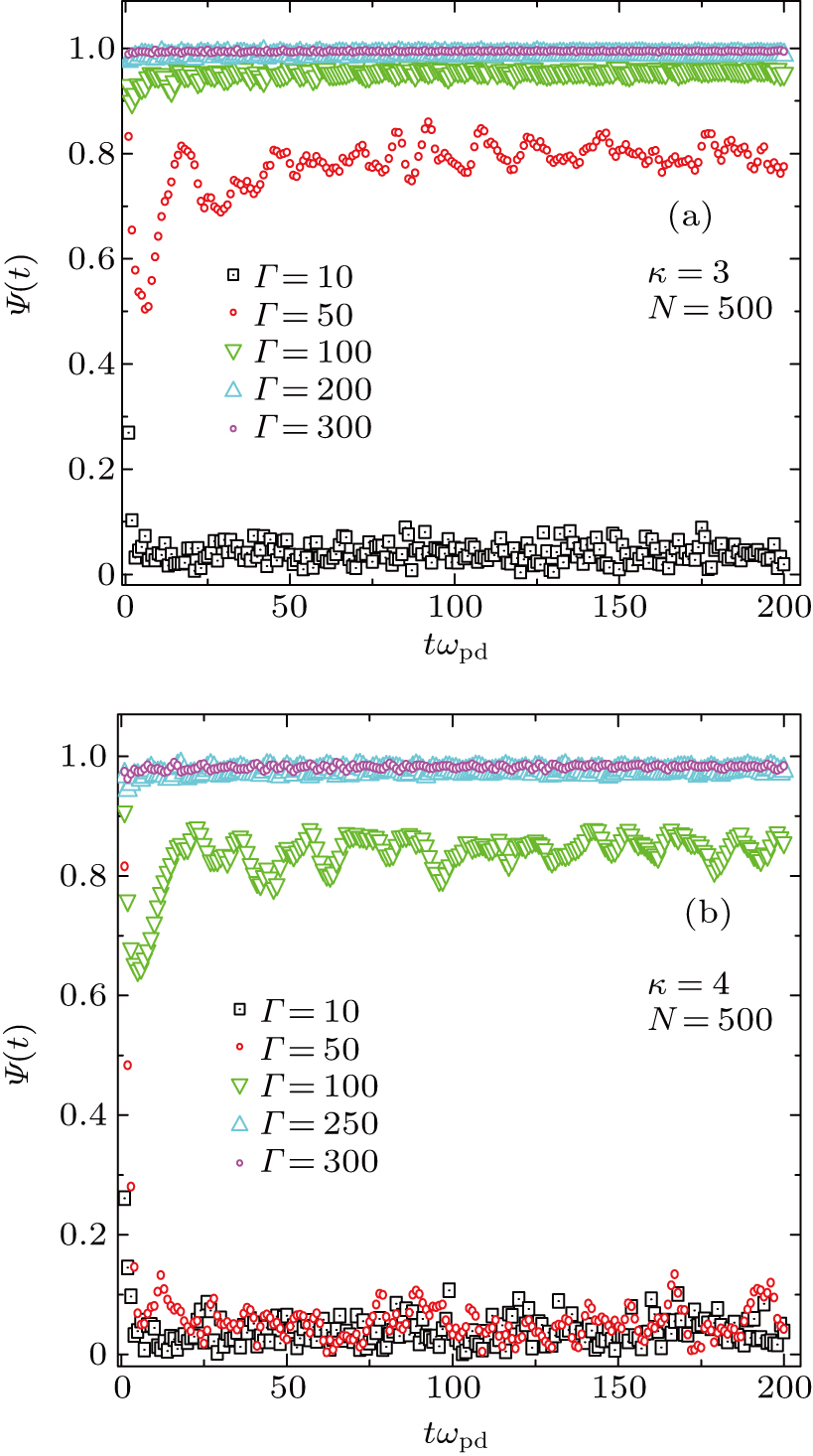
The presented main HEMD outcomes of plasma crystalline structure
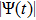 with BCC arrangements, shown in Figs. 1–4, are performed for N = 256 (for κ = 1.4 and 3), N = 500 (for κ = 3 and 4) and N = 864 (for κ = 1.4, 2, 3, and 4) dust particles at fixed value of scaled external force field of
with BCC arrangements, shown in Figs. 1–4, are performed for N = 256 (for κ = 1.4 and 3), N = 500 (for κ = 3 and 4) and N = 864 (for κ = 1.4, 2, 3, and 4) dust particles at fixed value of scaled external force field of
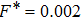 , for different plasma parameters of Γ= 10, 50, 100, 200, and 300. The steady state values of the dust particle crystalline structure
, for different plasma parameters of Γ= 10, 50, 100, 200, and 300. The steady state values of the dust particle crystalline structure
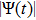 with BCC arrangements are computed over the appropriate combinations of the Coulomb strengths (Γ= 10, 300) and Debye strengths (
with BCC arrangements are computed over the appropriate combinations of the Coulomb strengths (Γ= 10, 300) and Debye strengths (
 , 4) at mentioned low value of scaled force field
, 4) at mentioned low value of scaled force field
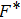 (= 0.002). It should be noted that the reported results of dust particle crystalline structure
(= 0.002). It should be noted that the reported results of dust particle crystalline structure
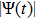 are compared and discussed with the earlier results taken from 3D HNEMD calculations of Shahzad and He[13, 26, 35, 39] as well as the crystalline structure trends taken from the theoretical estimations of Ikezi[14] which was already confirmed experimentally.[21–25, 28, 29] Moreover, our 3D HNEMD outcomes of plasma OD-structure
are compared and discussed with the earlier results taken from 3D HNEMD calculations of Shahzad and He[13, 26, 35, 39] as well as the crystalline structure trends taken from the theoretical estimations of Ikezi[14] which was already confirmed experimentally.[21–25, 28, 29] Moreover, our 3D HNEMD outcomes of plasma OD-structure
 are also discussed with those obtained in 3D complex plasma experimental outcomes.[21–25, 28, 29] It is noted that our new outcomes well-explain dust particle OD-structures trends and are in good agreement with the previous experimental outcomes obtained by various research groups and earlier numerical measurements based on different numerical techniques and show that the current HENMD technique is the best alternative choice to explains the OD-structures in different phases.
are also discussed with those obtained in 3D complex plasma experimental outcomes.[21–25, 28, 29] It is noted that our new outcomes well-explain dust particle OD-structures trends and are in good agreement with the previous experimental outcomes obtained by various research groups and earlier numerical measurements based on different numerical techniques and show that the current HENMD technique is the best alternative choice to explains the OD-structures in different phases.
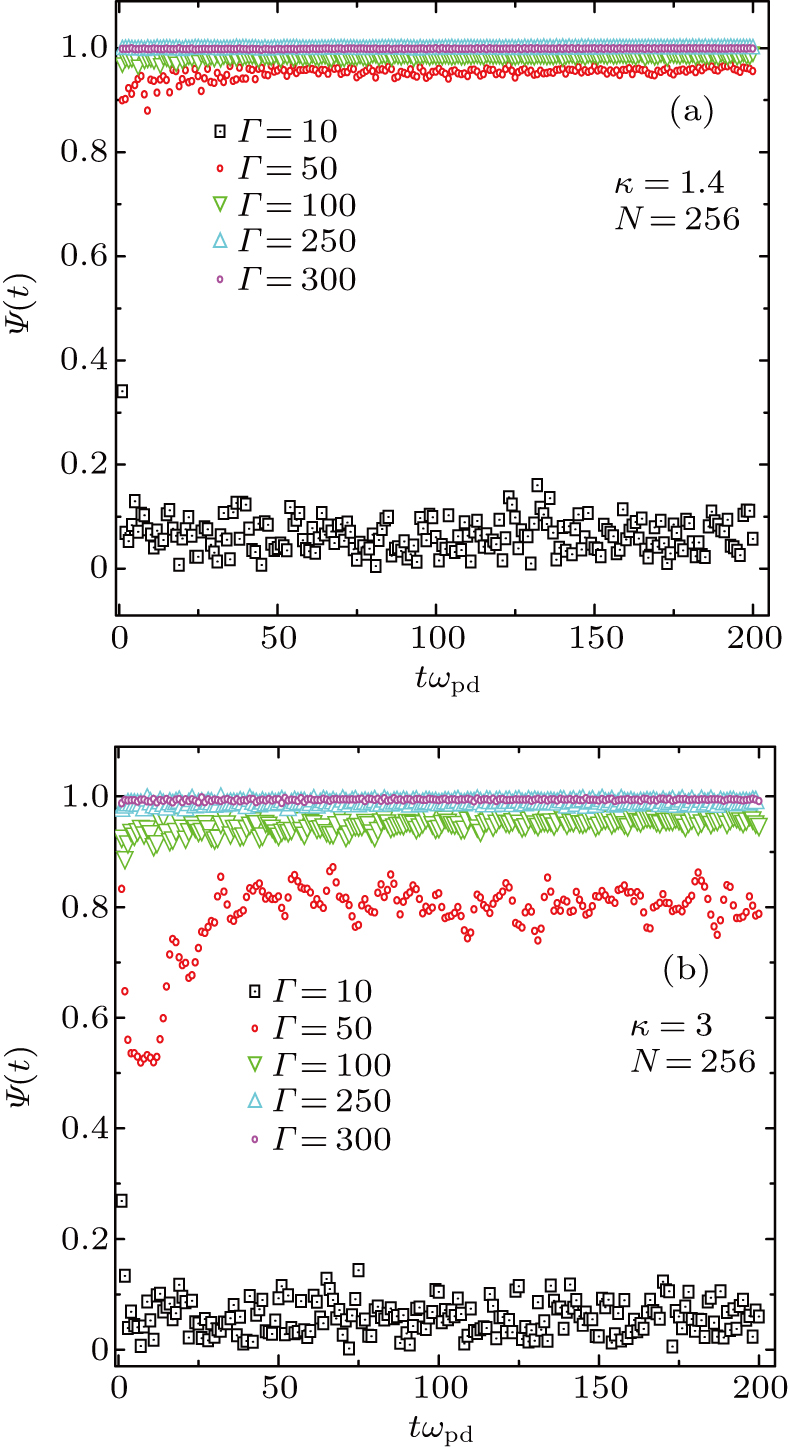
Figures 1 and 2 illustrate the dust particle lattice structure (crystalline OD-structure)
 varied with time (t /
varied with time (t /
 ) of SC-NICSs at constant scaled external force field strength of
) of SC-NICSs at constant scaled external force field strength of
 . For both cases, the
. For both cases, the
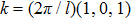 is the reciprocal lattice vector for BCC and has used in our HNEMD simulation scheme, where l is the edge length of the simulation box. We have carried out twenty different HNEMD simulations with five various combinations of plasma couplings of Γ= 10, 50, 100, 200, 250, and 300 and three varying values of screening parameter of κ = 1.4 and 3 (for N = 256) and κ = 3 and 4 (for N = 500) at constant
is the reciprocal lattice vector for BCC and has used in our HNEMD simulation scheme, where l is the edge length of the simulation box. We have carried out twenty different HNEMD simulations with five various combinations of plasma couplings of Γ= 10, 50, 100, 200, 250, and 300 and three varying values of screening parameter of κ = 1.4 and 3 (for N = 256) and κ = 3 and 4 (for N = 500) at constant
 . It is observed during HENMD scheme that these combinations of plasma states confirm the accuracy and reliability of the dust particle OD-structures in nonideal gas, liquid, and crystalline phases. It is examined from both figures that the dust particles in the complex plasma system are in fully order state, then, the lattice correlation shows
. It is observed during HENMD scheme that these combinations of plasma states confirm the accuracy and reliability of the dust particle OD-structures in nonideal gas, liquid, and crystalline phases. It is examined from both figures that the dust particles in the complex plasma system are in fully order state, then, the lattice correlation shows
 and the plasma system remains in the strongly coupled regime. It is clearly shown that the lattice correlation approaches to
and the plasma system remains in the strongly coupled regime. It is clearly shown that the lattice correlation approaches to
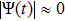 , which shows that the dust particles are in disorder state and the plasma system rests in nonideal gaseous state. It is observed from Figs. 1(b), 2(a), and 2(b) that the dust particles in the plasma system can exist between upper and lower limits of
, which shows that the dust particles are in disorder state and the plasma system rests in nonideal gaseous state. It is observed from Figs. 1(b), 2(a), and 2(b) that the dust particles in the plasma system can exist between upper and lower limits of
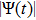 (i.e.,
(i.e.,
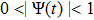 ) and it is demonstrated that the plasma system is in moderate order state and more probably above the intermediate line of
) and it is demonstrated that the plasma system is in moderate order state and more probably above the intermediate line of
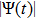 . It can be seen from Fig. 1(a) that the high degree of dust crystalline order (strongly coupled regime) persists throughout the observation time period (
. It can be seen from Fig. 1(a) that the high degree of dust crystalline order (strongly coupled regime) persists throughout the observation time period (
 ) for the higher Coulomb couplings (Γ= 100, 200, and 300) whereas the crystalline order completely vanishes (nonideal gaseous regime) for low couplings (Γ= 10) at κ = 1.4, confirming the earlier numerical outcomes.[13, 26, 35, 39] It is observed from Figs. 1(b) and 2(a) that high degree of crystalline order still exists for higher Γ(= 200, 250, and 300), however, degree of long range order decreases for Γ= 50 and 100, and high to moderate crystalline order is present for Γ= 50 and 100 at κ = 3, validating the previous OD-structures.[12–17, 26, 35, 39] Moreover, it is noted that high to moderate degree of long range order shifts to high Γ(= 100) and the disorder state transfers to Γ= 50 with an increase of κ = 4, as shown in Fig. 2(b), throughout the HNEMD simulation time, as expected. It is concluded from both cases that a moderate to high degree of crystalline order exists for higher Γ(= 100, 200, 250, and 300) during the complete simulation run, demonstrating the earlier numerical and experimental outcomes that for higher Γ, the SC-NICSs can be under the collective influence of dust particles, and the particles seek to stay cage or trapped near steady state locations centered along with close by neighbors and dust particle motion becomes slow enough, resultantly, the dust particles self organize in a crystalline-line structure.[41] Furthermore, for the Coulomb coupling range of
) for the higher Coulomb couplings (Γ= 100, 200, and 300) whereas the crystalline order completely vanishes (nonideal gaseous regime) for low couplings (Γ= 10) at κ = 1.4, confirming the earlier numerical outcomes.[13, 26, 35, 39] It is observed from Figs. 1(b) and 2(a) that high degree of crystalline order still exists for higher Γ(= 200, 250, and 300), however, degree of long range order decreases for Γ= 50 and 100, and high to moderate crystalline order is present for Γ= 50 and 100 at κ = 3, validating the previous OD-structures.[12–17, 26, 35, 39] Moreover, it is noted that high to moderate degree of long range order shifts to high Γ(= 100) and the disorder state transfers to Γ= 50 with an increase of κ = 4, as shown in Fig. 2(b), throughout the HNEMD simulation time, as expected. It is concluded from both cases that a moderate to high degree of crystalline order exists for higher Γ(= 100, 200, 250, and 300) during the complete simulation run, demonstrating the earlier numerical and experimental outcomes that for higher Γ, the SC-NICSs can be under the collective influence of dust particles, and the particles seek to stay cage or trapped near steady state locations centered along with close by neighbors and dust particle motion becomes slow enough, resultantly, the dust particles self organize in a crystalline-line structure.[41] Furthermore, for the Coulomb coupling range of
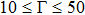 and
and
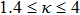 , it has been shown that crystalline order speedily vanishes, signifying the former outcomes[13, 26, 35, 39] that the dusty plasma system is under binary interactions and dust particles may not stay under caged action for a long time.[41] For intermediate Γ(= 50, for N = 256 and N = 500 at κ = 1 and 3), the dust particles may not line up in crystalline structure and it is positioned like a liquid or a nonideal gaseous state (Γ= 10 for κ = 1 to 4, and Γ= 50 for *
, it has been shown that crystalline order speedily vanishes, signifying the former outcomes[13, 26, 35, 39] that the dusty plasma system is under binary interactions and dust particles may not stay under caged action for a long time.[41] For intermediate Γ(= 50, for N = 256 and N = 500 at κ = 1 and 3), the dust particles may not line up in crystalline structure and it is positioned like a liquid or a nonideal gaseous state (Γ= 10 for κ = 1 to 4, and Γ= 50 for *
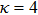 ).
).
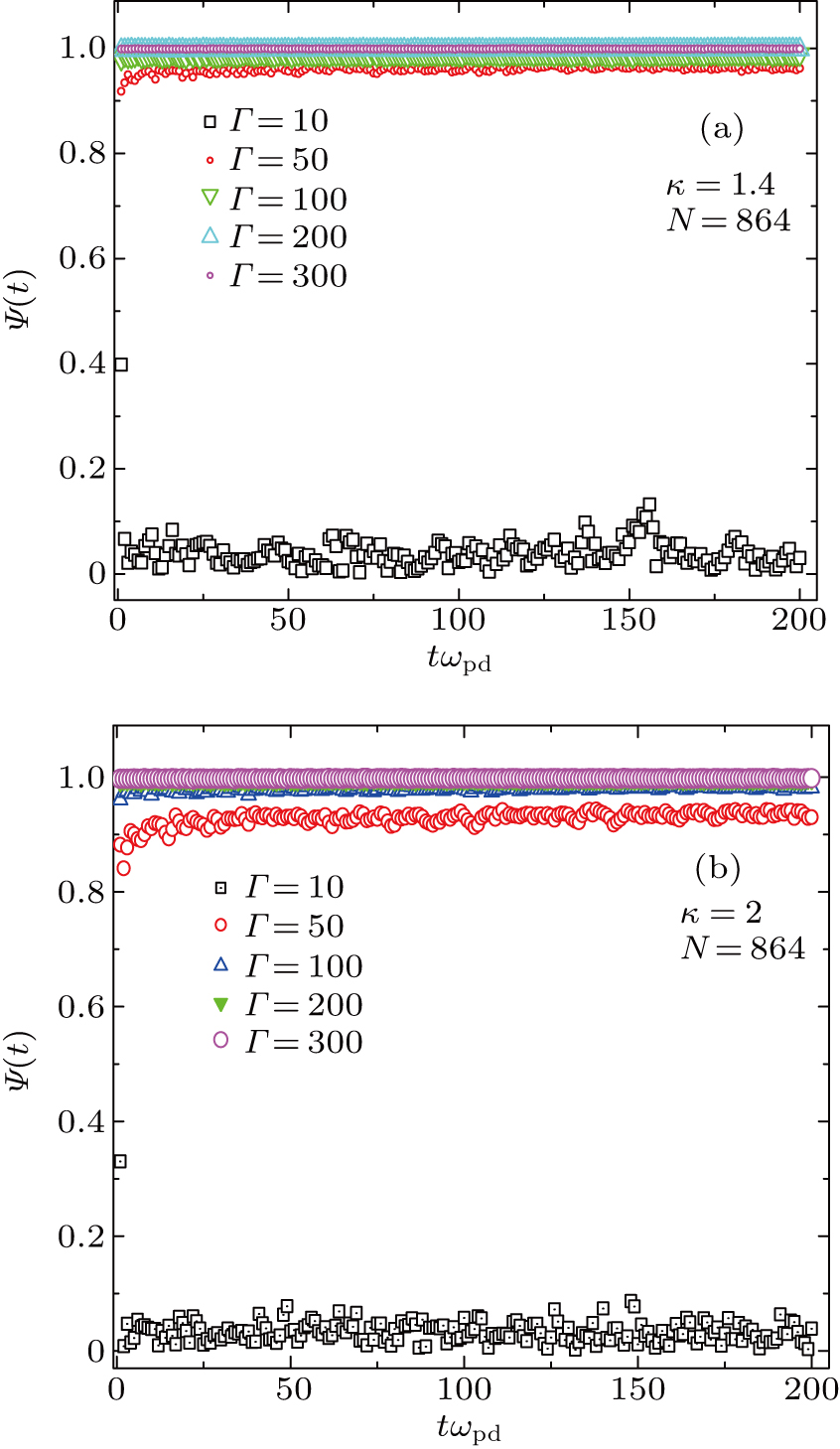
Two sets of Figs. 3 and 4 show the variations of particle crystalline lattice
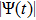 obtained from the density at any point r, as a function of simulation time (
obtained from the density at any point r, as a function of simulation time (
 ), setting N = 864 dust particles for the cases of κ = 1.4, 2, 3, and 4, respectively, for different plasma couplings of Γ= 10, 50, 100, 200, and 300. For both sets, we evaluate the total of twenty diverse HNEMD simulations sets with each other corresponding to constant external force field
), setting N = 864 dust particles for the cases of κ = 1.4, 2, 3, and 4, respectively, for different plasma couplings of Γ= 10, 50, 100, 200, and 300. For both sets, we evaluate the total of twenty diverse HNEMD simulations sets with each other corresponding to constant external force field
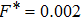 with reciprocal lattice vector for BCC. It is examined from four panels of both Figs. 3 and 4 that a high to moderate rank of crystalline order exists throughout the HNEMD simulation time (
with reciprocal lattice vector for BCC. It is examined from four panels of both Figs. 3 and 4 that a high to moderate rank of crystalline order exists throughout the HNEMD simulation time (
 ) but long range order shifts toward intermediate to high Γ(=50, 100) with increasing κ. It is interesting to note that the plasma system stays in disorder state for intermediate Γ(= 50) and in moderate order state for high Γ(= 100) at high screening value of
) but long range order shifts toward intermediate to high Γ(=50, 100) with increasing κ. It is interesting to note that the plasma system stays in disorder state for intermediate Γ(= 50) and in moderate order state for high Γ(= 100) at high screening value of
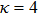 , confirming the earlier simulation results.[13, 26, 35, 39] At intermediate screening κ = 2, as shown in Fig. 3(b), the plasma system stays in the upper limit of high rank of long range order for intermediate Γ= 50. We have already advance a possible justification for this disorder state at intermediate Γ= 50 and high κ = 4 that the plasma system may be subjected under binary interactions and dust particles movement cannot stay under caged motion for such simulation run. It is benchmarked that the HNEMD scheme gives computations for particle crystalline
, confirming the earlier simulation results.[13, 26, 35, 39] At intermediate screening κ = 2, as shown in Fig. 3(b), the plasma system stays in the upper limit of high rank of long range order for intermediate Γ= 50. We have already advance a possible justification for this disorder state at intermediate Γ= 50 and high κ = 4 that the plasma system may be subjected under binary interactions and dust particles movement cannot stay under caged motion for such simulation run. It is benchmarked that the HNEMD scheme gives computations for particle crystalline
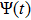 within the limited statistical uncertainties over the extensive plasma couplings Γ(=10, 300) with small system sizes and BCC lattice structure. It should be mentioned that the present HNEMD scheme is applied and covers the range of nonideal plasma coupling (Γ= 10) to strongly coupled range (Γ= 300), depending on κ.
within the limited statistical uncertainties over the extensive plasma couplings Γ(=10, 300) with small system sizes and BCC lattice structure. It should be mentioned that the present HNEMD scheme is applied and covers the range of nonideal plasma coupling (Γ= 10) to strongly coupled range (Γ= 300), depending on κ.
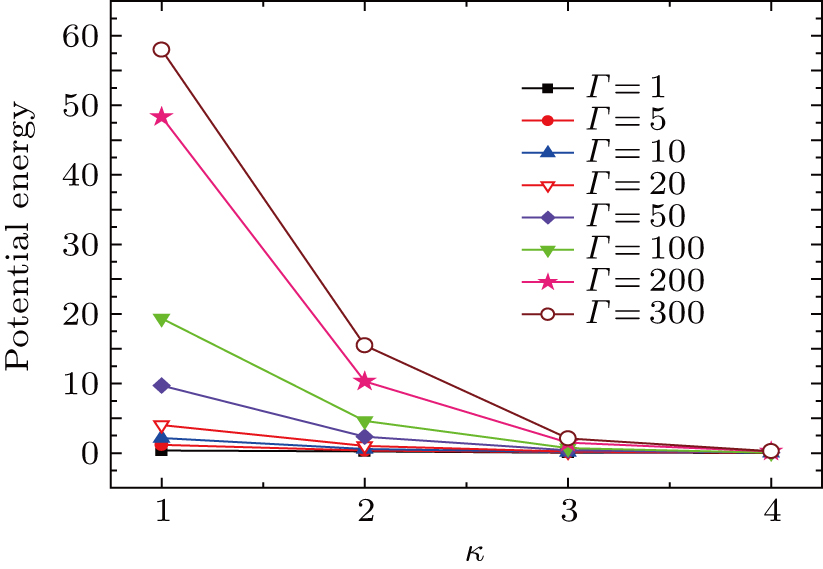
Figure 5 shows the variation of Yukawa PE versus the screening parameter (κ) for eight different plasma couplings of Γ= 1, 5, 10, 20, 50, 100, 200, and 300, which covers the nonideal state (Γ= 1, 5, and 10) to liquid (Γ= 50 and 100) and strongly coupled (Γ= 100, 200, and 300) regimes. It is clear from Fig. 5 that the PE has its maximum value for higher temperature at κ = 1 and it decreases correspondingly with increasing κ. For small plasma coupling regime
 (at high temperature and low density range), the dust particles achieve high kinetic energy (KE) as compared to PE and in this coupling regime the KE is dominated over the PE throughout the HNEMD simulation run (also see Figs. 1–4) and the plasma system remains in disorder state (nonideal gaseous state), however, it depends on the selection of κ and this regime extends up to
(at high temperature and low density range), the dust particles achieve high kinetic energy (KE) as compared to PE and in this coupling regime the KE is dominated over the PE throughout the HNEMD simulation run (also see Figs. 1–4) and the plasma system remains in disorder state (nonideal gaseous state), however, it depends on the selection of κ and this regime extends up to
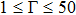 for κ = 4. Meanwhile, at an intermediate to higher plasma coupling regime
for κ = 4. Meanwhile, at an intermediate to higher plasma coupling regime
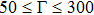 (intermediate to low temperatures and corresponding intermediate to high densities), the dust particle PE is dominated over the KE during the whole simulation run time (again also see Figs. 1–4) and the plasma system tends to stay in moderate to fully order state (strongly coupled regime). But this fully order regime cuts down to
(intermediate to low temperatures and corresponding intermediate to high densities), the dust particle PE is dominated over the KE during the whole simulation run time (again also see Figs. 1–4) and the plasma system tends to stay in moderate to fully order state (strongly coupled regime). But this fully order regime cuts down to
 for κ = 4 and the plasma system remains in liquid state for intermediate to high
for κ = 4 and the plasma system remains in liquid state for intermediate to high
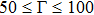 for κ = 2 and 3 and the dust particle PE may be balanced with KE. It is therefore concluded that the plasma system has its maximum PE and minimum KE for fully order crystalline state (strongly coupled regime); however, the plasma system has KEmin and PEmax for fully disorder state (nonideal gaseous state).
for κ = 2 and 3 and the dust particle PE may be balanced with KE. It is therefore concluded that the plasma system has its maximum PE and minimum KE for fully order crystalline state (strongly coupled regime); however, the plasma system has KEmin and PEmax for fully disorder state (nonideal gaseous state).
4. ConclusionAn alternative HNEMD scheme has been employed for the calculation of dust particle crystalline OD-structures in 3D SC-NICSs over a suitable wide range of plasma parameters (Γ, κ) at constant force field strength. The lattice correlation
 with BCC arrangements has demonstrated the presence of the exact dust particle crystalline structures in complex plasma systems. New investigations show that the dust particles in complex dusty plasma system have fully order state at high Γ(low temperature) and disorder state at low Γ(high temperature). This alternative scheme reveals that the dust particle crystalline depends on both plasma states (Γ, κ) and it is shown that a moderate to high rank of long range order shifts toward high Γwith an increase of κ. It has been shown that the PEmax is dominated over the KEmax for high rank of long range order (strongly coupled regime) and KEmax is influenced over the PEmax where for long range order disappears and it is a disorder state (nonideal gaseous state). It is concluded that the present HNEMD method is the best alternative choice to investigate the OD-structures of dust particles with small system sizes, in different phases such as nonideal gas, liquid, and crystalline, and has the best performance with comparable accuracy to that of the 3D GK-EMD and NEMD methods. For future work, this alternative method, which is based on Evans's approach, can be used to measure the OD-structures of the dust particle with an application of external electric and or magnetic fields, and can be applied for other complex systems.
with BCC arrangements has demonstrated the presence of the exact dust particle crystalline structures in complex plasma systems. New investigations show that the dust particles in complex dusty plasma system have fully order state at high Γ(low temperature) and disorder state at low Γ(high temperature). This alternative scheme reveals that the dust particle crystalline depends on both plasma states (Γ, κ) and it is shown that a moderate to high rank of long range order shifts toward high Γwith an increase of κ. It has been shown that the PEmax is dominated over the KEmax for high rank of long range order (strongly coupled regime) and KEmax is influenced over the PEmax where for long range order disappears and it is a disorder state (nonideal gaseous state). It is concluded that the present HNEMD method is the best alternative choice to investigate the OD-structures of dust particles with small system sizes, in different phases such as nonideal gas, liquid, and crystalline, and has the best performance with comparable accuracy to that of the 3D GK-EMD and NEMD methods. For future work, this alternative method, which is based on Evans's approach, can be used to measure the OD-structures of the dust particle with an application of external electric and or magnetic fields, and can be applied for other complex systems.
Acknowledgment
We are grateful to the National Advanced Computing Center of National Center of Physics (NCP), Pakistan, for allocating computer time to test and run our MD code.