† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11872033) and the Beijing Natural Science Foundation, China (Grant No. 3172017).
The simulation of real contact area between materials is foundationally important for the contact mechanics of mechanical structures. The Greenwood and Williamson (GW) model and the Majumdar (MB) model are the basic models in this field, which are widely accepted and proven to be valid in many experiments and engineering. Although the contact models have evolved considerably in recent years, the verifications of the models are most based on the indirect methods such as electrical conductivity and contact stiffness, because of the lack of effective methods to directly measure the variation of contact surface. In this paper, the total reflection (TR) method is introduced into the verification of contact models. An experiment system based on TR method is constructed to measure the real contact area of two PMMA specimens. The comparison analysis between the results of experiment and models suggests that the experiment result has the same trend with simulation, the MB model has better agreement with the experimental result because this method can take into account the variation of radius and the merging of asperities, while the GW model has a huge deviation because of the dependence on resolution and the lack of considering the variation of radius and asperity’s merging process. Taking the interaction of asperities into account could give a better result that is closer to the experiment. Our results and analysis prove that the experimental methods in this paper could be used as a more direct and valid method to quantitatively measure the real contact area and to verify the contact models.
A model of the real contact area between materials is foundationally important for the friction, sliding, seals, wear, structure stiffness and damping, thermal and electrical conductivity, and other aspects of engineering.[1–3] This subject has attracted interest of researchers for over 500 years. In 1495, when Leonardo da Vinci first found the fundamental laws of friction by experimenting with ball-bearings, revealing that the frictional force is independent of the contact surfaces.[1] In 1699, Amontons rediscovered the laws of friction and in 1781 Coulomb enriched and systematically summarized the laws.[1] The recently most important contribution was made by Bowden and Tabor in 1939, who found that the real contact area between two materials consists of a myriad of contact asperities, and is orders of magnitude smaller than the nominal contact area.[4] Based on this theory, in 1966 Greenwood and Williamson (GW) proposed the pioneering GW model, which simulates the real contact area by integrating the contact area of single asperity under normal pressure, assuming that the height of asperities varies randomly comply with the Gaussian distribution, every asperity summit has the same curvature radius, the asperities are independent of each other, and the deformation is mainly elastic. Despite the crudeness of the GW model, it has been widely applied and validated by many experiments, and leaded to many derivative models, such as the WA model proposed by Whitehouse and Archard (WA) in 1969 by considering the distribution of asperity curvature,[6] the OA model proposed by Onions and Archard (OA) in 1972 by utilizing the WA model to determine the relationship between the separation and contact area,[7] and many other models considering new factors for the special problems.[8,9] However, many of the parameters of these models are determined by the resolution of apparatus, such as roughness and profile of surface, which will cause the un-uniqueness of the results. In 1991, Majumdar argued that the mechanic surface has self-affine fractal characteristics, and proposed the contact fractal theory and the corresponding MB contact model, in which the major parameters fractal dimension D and characteristic length scale G are scale invariance. This characteristic will guarantee the uniqueness of results.[10] The MB model also has been widely applied to structure stiffness and damping simulation and proved to be valid in the prediction of stiffness and damping of the mechanic contact surface.[11,12] Despite the different interpretation for contact surface, GW model and MB model both have many supporters, and in recent years some new more accurate models have been proposed by researchers based on these two models. For example, the Zhao, Maietta, and Chang (ZMC) model is based on the GW model considering the transition from elastic deformation to fully plastic flow,[13] the Kogut and Etsion (KE) model also based on GW model considers the interaction of neighboring asperities,[14] Persson's model inheriting from multi-scale principle of MB model can take the interaction into account from the special physical view of contact diffusion,[23–25] and the newest paper[15] considered the interaction of asperities based on the MB model.
Although the contact models have evolved considerably, the verifications of these models are most based on the indirect methods, such as electrical conductivity and contact stiffness.[11–15] Whereas, directly observing the real contact area between two bodies should be a more accurate experimental method to measure the variation of the contact surface under different load, and to verify the contact models. Along with the improvements in the technique, researchers have recently tried to directly observe the contact surface using advanced techniques. For example, Eguchi analyzed the interface distribution of the contact area by using white light interference.[16] Tuononen used a high-speed camera to record the contact area of interface between rubber sample and the glass surface.[17] However, these methods can only measure the contact interface between the transparent material and non-transparent material. Kim presented a method that can predict the real contact area between solids by utilizing the data from ultrasonic measurement.[18] Bettscheider proposed a foot-printing approach to determine the real contact area by measuring the foot-printing on a thin marker layer on the interface.[19] However, these methods are a little complicated and hard to realize. Rubinstein, in 2004, proposed a total reflection (TR) method to observe the real contact surface, which is based on the optical theory that the light only passes through the contact asperities between two transparent materials when the angle of incidence is greater than the critical angle.[20] The TR method has been proven to be easy to implement, and effective in the observation of real contact area between two transparent materials, which are testified by some breakthrough discoveries based on this method.[21]
In this paper, an experiment system based on TR method is constructed to measure the real contact area of two polymethyl methacrylate (PMMA) specimens, the variation of real contact area under normal force is quantitatively studied by experiment and simulation using GW model and MB model.
The rest of this paper is organized as follows. Section
Although some new revised formulas in recent years have been proposed to calculate the real contact area and related stiffness and damping of contact surface,[13–15] the principle can almost all stem from the two basic models: GW model and MB model. In this section, these two basic models will be introduced and analyzed. Because the definition about real contact area has different meaning in different research scale.[29–31] To avoid ambiguity, we defined here that real contact area means the area having true contact between two surfaces, and nominal contact area means the shape of the surface which appears to contact.
Since Bowden and Tabor in 1939 found that the real contact area between two materials consists of a myriad of contact asperities,[4] how to determine the deformation of asperities and how to calculate the distribution and the variation of asperities have attracted much interest. The Hertz contact theory is classical and widely accepted for the elastic deformation of sphere contact, and is generally used to calculate the elastic deformation of asperities.[5] As shown in Fig.
 | Fig. 1. The deformation of sphere and flat rigid plane, R is the radius of asperity, δ is the normal deformation, Aa is the area of deformation, and Pa is the normal force. |
Based on this contact theory, and considering that the deformation of asperities is major elastic, in 1966, Greenwood and Williamson proposed the GW model, which assumed that the height distribution of peaks of asperity is Gaussian, the radii of peaks all equal to the mean radius of curvature, and the asperities are all independent of each other. On the basis of these assumptions, a simple relationship about normal force and real contact area can be obtained, as shown in Fig.
The probability of an asperity having real contact area 
Therefore, the total real contact area can be acquired by summing the possible contact areas of all asperities as
Following this method, the total normal force can be obtained by
Although the GW model is simple and proven to be valid in many contact cases,[5–9] the accurate parameters such as height, radius, density, and variation of height are determined by the resolution of measurement apparatuses and hard to be obtained. For example, the density of asperity is difficult to be determined if the asperities have no obvious separation line, and will change with the resolution. In 1999, Majumdar argued that although the topography of surface will change with the resolution of measurement, the topography in different scale is self-affine which is similar to the self-similar of topography of earth surface. Based on this discovery, they introduced the fractal theory into contact surface and developed the MB model.[10]
The MB model uses two major parameters to depict the topography of an asperity: the fractal dimension D and the characteristic length scale G, which can be used to express the profile of a surface by utilizing Weierstrass–Mandelbort (WM) function


When thinking about the profile of a single asperity, which has a contact length 
Because the position x = 0 can be deemed as the center point of an asperity, then the radius of a single asperity can be obtained by
In the MB model, the size distribution of contact asperities is deemed to be the same with the distribution of the islands on earth. When normalizing Eq. (
Therefore, the distribution density can be obtained by the differentiation of Eq. (
Actually, the deformation will become plastic when the deformation of asperity increases beyond the critical value δc given by[10]
In the MB model, R is determined by Eq. (
Likewise, for the MB model, the critical value of contact area Ac can be derived out by combining Eqs. (
Analyzing Eq. (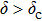
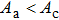

Despite the different interpretation, the GW model and MB model both obtain many supports from researchers and are proven to be valid in many cases calculating the stiffness and damping.[14,15] However, neither stiffness nor damping is a direct indicator to verify the formula, while measuring the real contact area would give a more direct experimental measurement for these formulas. In the next sections, an experiment setup is constructed to measure the real contact area based on the TR method, and the qualitative comparison analysis between simulation and experiment will be implemented.
The beam transmitting from a denser medium to a thinner one will be totally reflected back into the denser medium when the incident angle is greater than the critical angle.[20] As shown in Fig.
Based on this principle, we build an experiment setup to measure the contact area under normal force. As shown in Fig.
| Table 1.
Parameters of major devices and material. . |
The experiment is carried out, the camera is set to manual mode at ISO 2200 and f 4.0, the sampling rate of normal force is 1024 with low-pass filtering at 30 Hz. To ensure that the surface is enough flat and transparent, the nature surface of PMMA block without other polishing is utilized as the experimental surface. The normal load increases at constant speed and stops at every test point. To avoid the creep of PMMA, we only take three photos at every test point to obtain the average greyscale in very short time interval, about several seconds. The recorded images are shown in Fig.
In this section, the surface topography is scanned by the white light interferometer, and the surface parameters used to calculate the real contact area are calculated based on the obtained image, the curve of normal force and real contact area obtained from GW model, MB model, and experiment are plotted in a graph to comparatively analyze the results.
The white light interferometer shown in Fig. 
For the MB mode, the parameters D and G can be obtained from the power spectrum of profile of surface, which can be expressed as
In the log–log coordinate, the curve of ω and F(ω) is an approximate straight line. If the slope is in the range of −3 to −1, the surface is deemed to be fractal, and D and G can be calculated using the slope and intercept of line as
The resulting parameters for the two models and the characteristic parameters of material are listed in Table
| Table 2.
Parameters of models and material. . |
The parameters are substituted into the models, and the results of experiment and simulation are plotted in Fig.
At small load, deformation is small and the asperity is well separated, so the GW and MB models would have a good prediction, this is generally accepted and verified by many researchers. For example, Hyun proved that the relationship of real contact area and load is linear when the fraction of contact area is smaller than 0.1,[22] our experimental result also agrees with this. Although Persson had a different opinion for the contact model, he also admitted that the GW model and MB model are accurate at small load.[23]
What causes the big deviation to the GW model in the small load region? We can obtain two explanations from the paper about MB model.[10] One is that the parameters of GW model will be greatly affected by the resolution of measurement devices. The white interferometer used in this experiment has the resolution of 0.1 nm, which is significant higher than that of the experiment finished in the past time. Persson also argued that GW model just considers one scale of the surface which is not very accordance with the reality;[23] i.e., the resolution for GW model should be in a matched scale. Another explanation is that the GW assumes a constant radius, which is not consistent with the reality and also the phenomena in our experiment where strip cluster is obvious even in small load area. In contrast, the MB model takes into account the change of radius and the merging of neighboring asperities, which is more reasonable at least for this experiment where the asperities emerging phenomenon is also evident as shown in Fig.
It also can be noticed that MB model has an increasing deviation to the experiment result. Persson thought that GW and MB both lack the ability to model the interaction of asperities,[23–25] which will greatly affect the result at heavy load. Some other researchers also pointed out this problem and proposed revised models. For example, Zhao derived the revised method by utilizing the Saint–Vansant's principle and proved that the revised model has a larger contact area than the original GW model under the same load.[13] Tang proposed a numerical iterative method to model the interaction of the asperities, and showed that in the revised mode, the deformation of asperities would be larger than that in the original model which is based on GW model.[28] Likewise, following this revised method, if the interaction is taken into account in the MB model, then the curve would be more close to the experiment result. Persson also proposed a new multi-scale model from different physical angle,[23,24] which derived an equation similar to the diffusion function to depict the process of real contact area changing with scale and load, and argued that it can take into account the elastic coupling between asperities and is more accurate than the GW and MB models.[24] A problem should be noticed that the MB model takes every scale of surface into account; however, it can be observed in the color images of Fig.
From the results and analysis, it can be concluded that the total reflection method and the related experimental method in this paper would be valid to be used as a quantitative method for the real contact area measurement. Based on this direct measurement method, the researcher not only can analyze the evolution of interface under different load and condition but can also compare and verify many revised contact models and newly developed contact models. This experimental method has foundational value for research of contact mechanisms and the related interface character.
The direct observation method for real contact area, TR method, is used to quantitatively verify the original GW model and MB model. The experiment system based on TR method is constructed to measure the real contact area of two PMMA specimens, the curves of real contact area and normal force obtained by the experiment and models are plotted in the same coordinate, the comparison analysis suggests that the MB model has better agreement with the experimental result because this method can take into account the variation of radius and the merging of asperities, while the GW model has a huge deviation because of the dependent on resolution and the lack of consideration of the variation of radius and asperity's merging process. If we take the interaction of asperities into account, then the results of models would have better agreement with the experiment. The results and analysis prove that the experimental methods in this paper could be used as a more direct and valid method to quantitatively measure the real contact area and to verify the contact models. This experimental method has the foundational value for research of contact mechanisms and the related interface character.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] |











