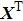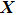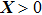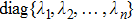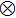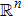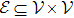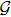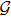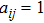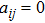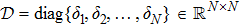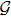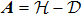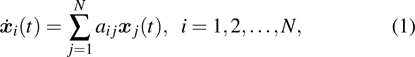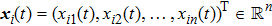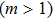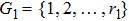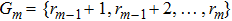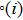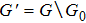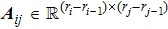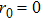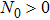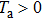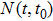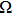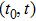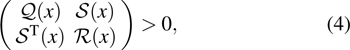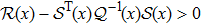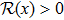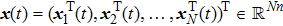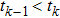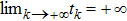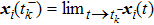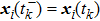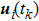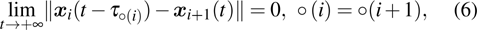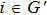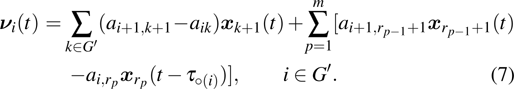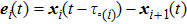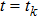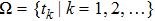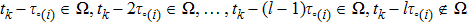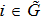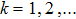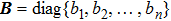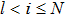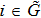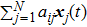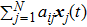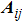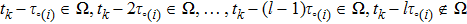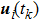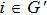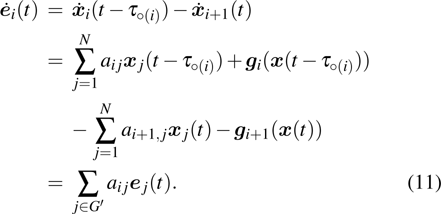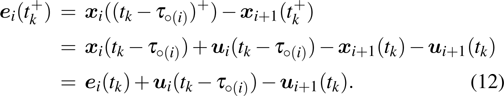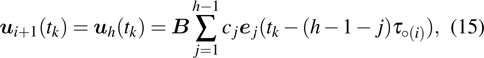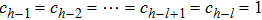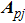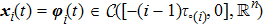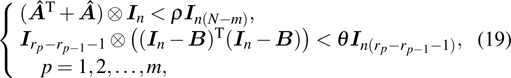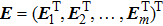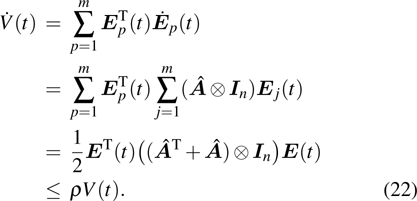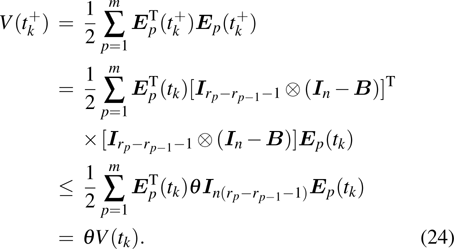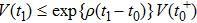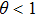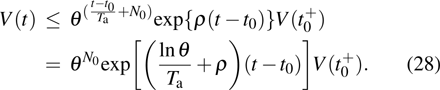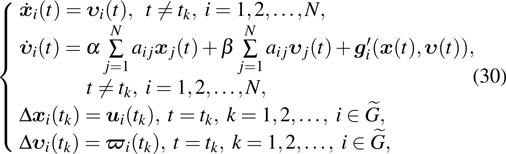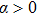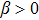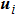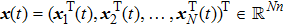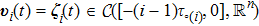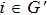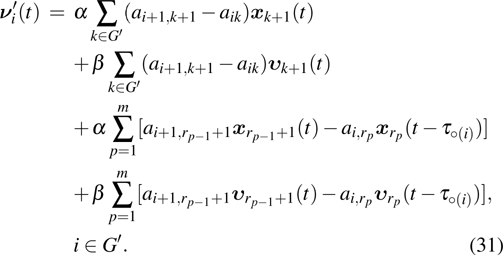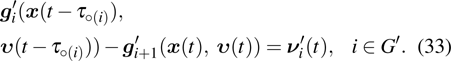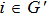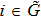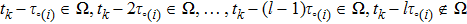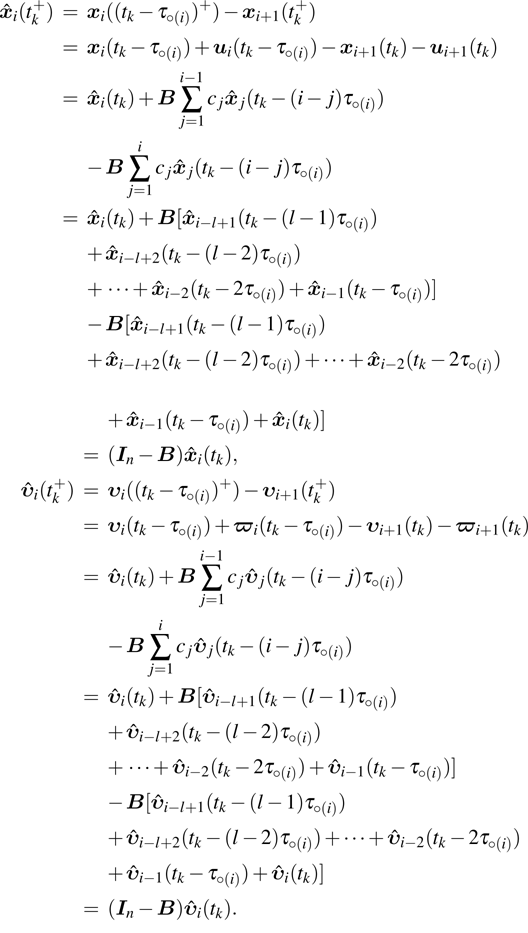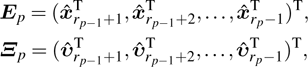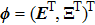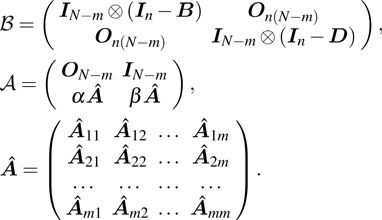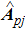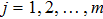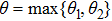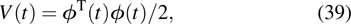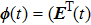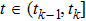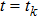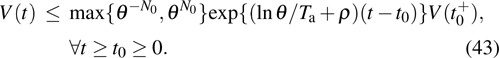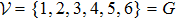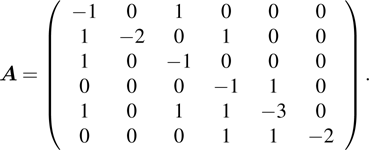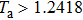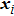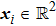Successive lag cluster consensus on multi-agent systems via delay-dependent impulsive control
1. IntroductionOver the past two decades, multi-agent systems have attracted extensive attention due to their applications in fields such as unmanned aerial vehicle,[1] formation control,[2,3] bio-science,[4,5] and so on. In Ref. [6], by utilizing the numerical simulation, Vicsek et al. discovered an interesting phenomenon in that the direction of movement of all particles can achieve consensus for a discrete-time model with small noise and higher density. Subsequently, based on the algebraic graph theory, a theoretical result of consensus for the Vicsek model was derived.[7] In Ref. [8], Ren and Beard have proven that discrete-time and continuous-time multi-agent systems can realize consensus if there is a spanning tree on a fixed or switched topology. Thereafter, lots of researchers expanded and enriched the consensus theory using different models and methods.[9–13]
In communication engineering, the states of agents may achieve lag consensus by noise interference. The lag consensus means that the consensus is realized on two different systems (i.e., leader–following multi-agent systems) with a time delay. Recently, the lag consensus on second-order multi-agent systems under adaptive feedback control was considered.[14] In Ref. [15], by applying a pinning control which is designed with local information from leader and agents, Wang et al. obtained that the second-order multi-agent systems can realize lag consensus. Furthermore, in Ref. [16], Li et al. introduced the successive lag consensus (SLC), which is a generalized consensus pattern of lag consensus. Compared with lag consensus, successive lag consensus is discussed in a system (or network), while the former is defined between two systems (or networks).
The cluster is a common phenomenon in social and biological networks. In Ref. [17], Qin and Yu studied the cluster consensus of multi-agent systems by distributed feedback control, based on graphic topology conditions. Some structural conditions on the basis of coupling strength and coupling matrix were proposed to achieve the cluster consensus of multi-agent systems.[18,19] Moreover, the cluster lag consensus of first-order multi-agent systems under distributed control was also studied.[20] In Ref. [21], the authors studied the cluster lag consensus of second-order multi-agent systems with switching topologies because there was a strongly connected digraph in each cluster. Inspired by these works, we will introduce a novel consensus pattern: successive lag cluster consensus (SLCC), which means that the SLC appears in each cluster of a network. There are many beautiful scenes of SLCC in nature. For example, birds will separate into several flocks (clusters) by some disturbances. The birds will then fly simultaneously in succession to avoid collision in each cluster. Another example is to make the traffic flow run smoothly.[20,21] The SLCC is a generalized pattern of lag cluster consensus. Studying the SLCC can solve the problem of traffic jam and avoid collision between the vehicles.
In this paper, the SLCC on multi-agent systems with directed graph is considered. Due to the low cost and robustness of the impulsive control, we solve the problem of SLCC on multi-agent systems by applying the delay-independent impulsive control. First, based on graph theory and stability theory, a sufficient condition for the stability of SLCC on first-order multi-agent systems is obtained. Second, we gain a sufficient condition of SLCC on second-order multi-agent systems by applying the Lyapunov stability theory. Finally, several numerical simulations are given to verify the theoretical results.
This paper is organized as follows. In Section 2, some preliminaries about graph theory and some basic definitions are given. In Section 3, the SLCC of first-order multi-agent systems under delay-dependent impulsive control is addressed. In Section 4, the globally exponential stability of SLCC on second-order multi-agent systems is investigated. In Section 5, some numerical examples are illustrated to verify the effectiveness of the proposed delay-independent impulsive control. In Section 6, the conclusion is given.
The following notations are used.
 and
and
 denote the n × n identity matrix and zero matrix, respectively.
denote the n × n identity matrix and zero matrix, respectively.
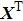 is the transpose of matrix
is the transpose of matrix
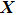 . Matrix
. Matrix
 is positive definite if
is positive definite if
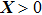 . Let
. Let
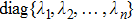 be an n × n diagonal matrix, where
be an n × n diagonal matrix, where
 are diagonal elements.
are diagonal elements.
 stands for Euclidean norm.
stands for Euclidean norm.
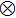 denotes the Kronecker product.
denotes the Kronecker product.
 is a set of all continuous functions from
is a set of all continuous functions from
 to
to
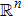 , where
, where
 .
.
2. PreliminariesThe directed graph of a multi-agent system with size N can be defined as
 , where
, where
 is the set of agents and
is the set of agents and
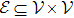 is the set of edges. An ordered pair
is the set of edges. An ordered pair
 of graph
of graph
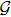 if and only if the i-th agent can receive information from the j-th agent directly, where the i-th agent is the goal agent and the j-th agent is an initial agent. If the graph
if and only if the i-th agent can receive information from the j-th agent directly, where the i-th agent is the goal agent and the j-th agent is an initial agent. If the graph
 is strongly connected, then there is a path between any two agents.
is strongly connected, then there is a path between any two agents.
 is the adjacency matrix of graph
is the adjacency matrix of graph
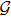 , where
, where
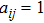 for
for
 , otherwise
, otherwise
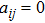 . The diagonal elements are defined as
. The diagonal elements are defined as
 . The degree matrix of graph
. The degree matrix of graph
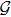 is
is
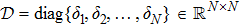 , where
, where
 ,
,
 . Then the coupling matrix of graph
. Then the coupling matrix of graph
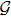 is
is
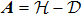 .
.
A general model of first-order multi-agent systems is given as
where
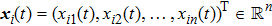
is the state variable of the
i-th agent at time
t.
To study SLCC, we first divide the set of agents
 into m
into m
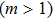 nonempty subsets
nonempty subsets
 , where
, where
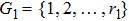 ,
,
 ,
,
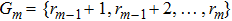 . We also call Gi as the i-th cluster. Our goal is to realize SLC among agents in each cluster. For
. We also call Gi as the i-th cluster. Our goal is to realize SLC among agents in each cluster. For
 , let
, let
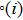 be the subscript of the cluster to which the agent i belongs, i.e.,
be the subscript of the cluster to which the agent i belongs, i.e.,
 .
.
 is the set of all agents without control and
is the set of all agents without control and
 is the set of the last agent of each cluster. Let
is the set of the last agent of each cluster. Let
 ,
,
 , and
, and
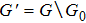 . Based on the above division, the coupling matrix can be rewritten accordingly as
. Based on the above division, the coupling matrix can be rewritten accordingly as
where each block matrix
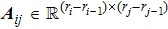
,

. When

, we let
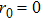
.
Definition 1[22] The average impulsive interval of impulsive sequence
 is equal to
is equal to
 , if there exist
, if there exist
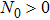 and
and
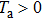 , such that
, such that
where
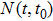
denotes the number of impulsive times of the impulsive sequence
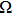
in the interval
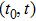
.
Lemma 1[23] For any
 and any positive-definite matrix
and any positive-definite matrix
 , we have
, we have
Lemma 2[24] The linear matrix inequality
where

,

, is equivalent to one of the following conditions:
1)
 ,
,
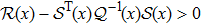 ,
,
2)
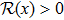 ,
,
 .
.
3. SLCC of first-order multi-agent systemsIn this section, to achieve SLCC on first-order multi-agent systems (1), we introduce some suitable coupling functions and delay-dependent impulsive controllers. Based on the stability theory, we will discuss the globally exponentially SLCC of first-order multi-agent systems.
The first-order SLCC protocol in multi-agent systems under impulsive control is described by
where
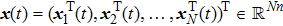
.

is an impulsive sequence, and
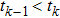
,
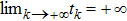
.

,

, and
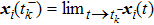
. For simplicity, we assume
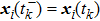
, which means

is left-hand continuous.
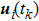
is the impulsive control input of the
i-th agent at
tk. And

is the coupling function which will be determined later.
Definition 2 If for any initial condition
 , we have
, we have
then the SLCC of first-order multi-agent systems (
5) is said to be achieved, where the consensus delay

,
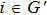
.
According to Definition 2, the cluster consensus manifold of system (5) can be given as
 . Some preliminary functions and coupling functions will be introduced to ensure the invariance of the cluster consensus manifold (the proof about invariance is given in Appendix A). First, some preliminary functions are defined by
. Some preliminary functions and coupling functions will be introduced to ensure the invariance of the cluster consensus manifold (the proof about invariance is given in Appendix A). First, some preliminary functions are defined by
Next, the coupling functions are given as
Then we have
According to Definition 2, the SLCC error of system (5) can be defined as
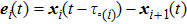 , for
, for
 ,
,
 . When
. When
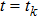 , from the SLCC error
, from the SLCC error
 , though
, though
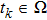 , we can not affirm that
, we can not affirm that
 belongs to impulsive sequence
belongs to impulsive sequence
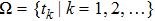 . Hence, we make the following assumption.
. Hence, we make the following assumption.
Assumption 1 There exists a positive integer
 , such that
, such that
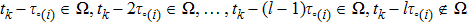 , where
, where
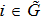 ,
,
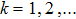 .
.
Based on the SLCC error and Assumption 1, the impulsive controllers can be designed as
where
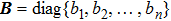
is an impulsive gain matrix and the constants
cj are defined as

,

, for
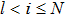
and
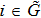
.
Remark 1 By applying the consensus protocol
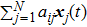 , the invariance of complete consensus manifold can be obtained in general model of first-order multi-agent systems (see Refs. [8] and [9]). However, for SLCC, the invariance can not be achieved if the consensus protocol
, the invariance of complete consensus manifold can be obtained in general model of first-order multi-agent systems (see Refs. [8] and [9]). However, for SLCC, the invariance can not be achieved if the consensus protocol
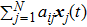 is used alone. So, due to the feature of SLCC, the coupling functions (8) are introduced to ensure the invariance of the cluster consensus manifold.
is used alone. So, due to the feature of SLCC, the coupling functions (8) are introduced to ensure the invariance of the cluster consensus manifold.
Remark 2 In Refs. [17]–[21], to achieve cluster consensus, every block matrix of
 must be a zero-row-sum matrix. In this paper, there is no strict limitation to each block matrix
must be a zero-row-sum matrix. In this paper, there is no strict limitation to each block matrix
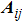 because we can ensure the invariance of cluster consensus manifold by coupling functions (8) (see Appendix A).
because we can ensure the invariance of cluster consensus manifold by coupling functions (8) (see Appendix A).
Remark 3 From Eq. (10), when
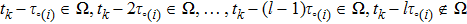 , some delay-dependent controllers
, some delay-dependent controllers
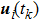 are designed, where
are designed, where
 and
and
 . This means that the agents
. This means that the agents
 and the first agent of each cluster are not controlled. According to the SLCC error and Assumption 1, we introduce a delay-dependent impulsive control to accelerate the implementation of SLCC.
and the first agent of each cluster are not controlled. According to the SLCC error and Assumption 1, we introduce a delay-dependent impulsive control to accelerate the implementation of SLCC.
For
 ,
,
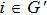 , the error system can be shown as
, the error system can be shown as
From Assumption 1, if

, then
Denote

, we obtain

. Accordingly, we have
where the constants
cj are defined as

,

. Therefore, equation (
13) can be rewritten as
We set
h=
i+1. According to the SLCC error, one has

. From Assumption 1,

, we have
where the constants
cj are defined as
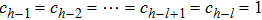
,

. Thus, equation (
15) can be rewritten as
By combining Eqs. (
12), (
14), and (
16), we obtain
Let
 . Then, the error system can be rewritten as
. Then, the error system can be rewritten as
where

is the rest of block matrix
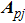
by deleting its last column and last row,

,

.
Remark 4 In Refs. [16] and [25]–[27], the synchronization delay τ is a fixed positive constant. In this paper, the agents are divided into m parts to realize SLC of each cluster with different consensus delay
 ,
,
 . When the agents i and j belong to different clusters, we do not pay attention to whether they can achieve lag consensus. That is to say, the SLC on multi-agent systems with variable consensus delay has been transformed into an m-cluster problem.
. When the agents i and j belong to different clusters, we do not pay attention to whether they can achieve lag consensus. That is to say, the SLC on multi-agent systems with variable consensus delay has been transformed into an m-cluster problem.
Definition 3 Globally exponentially SLCC of multi-agent systems (5) is achieved (that is the error system (17) is globally exponentially stable) for
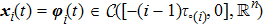 , if there exist
, if there exist
 ,
,
 , and
, and
 , such that
, such that
holds for all

,

.
Let
then the following theorem can be obtained.
Theorem 1 If there exist real number ρ and
 such that
such that
then the SLCC of first-order multi-agent systems (
5) under dependent-delay impulsive control (
10) can be achieved for any initial conditions.
Proof Define the following Lyapunov function:
When
 , letting
, letting
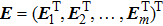 , the derivative of V(t) along trajectories of error system (17) can be given as
, the derivative of V(t) along trajectories of error system (17) can be given as
Hence, we obtain
When
 , we obtain
, we obtain
Combining inequalities (23) and (24), further results are given as follows.
For
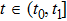 ,
,
 . Then, we have
. Then, we have
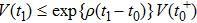 and
and
 . For
. For
 ,
,
 . So, in general, for
. So, in general, for
 , we obtain
, we obtain
From Definition 1, we know
Therefore, if
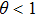
, combining inequalities (
25) and (
26), we have
If

, we obtain
Hence, for any

, we obtain
Since
 , for
, for
 , from inequality (29), we have
, from inequality (29), we have
Thus, according to Definition 3, the error system (
17) is globally exponentially stable under delay-dependent impulsive control (
10), then the first-order multi-agent systems (
5) can achieve SLCC. This completes the proof.
Remark 5 We do not consider the interrelation between successive lag cluster consensus and connectivity of graph
 in this paper. For example, it seems indeterminate about the relation between the feasible solution of inequalities (19) and (20) and existence of spanning tree of graph
in this paper. For example, it seems indeterminate about the relation between the feasible solution of inequalities (19) and (20) and existence of spanning tree of graph
 . This important interrelation will be researched in the future works.
. This important interrelation will be researched in the future works.
4. SLCC of second-order multi-agent systemsIn this section, we will discuss the SLCC of second-order multi-agent systems under delay-dependent impulsive control.
Based on the models in Refs. [28] and [29], the second-order SLCC protocol in multi-agent systems under impulsive control can be described as
where

and

are the position and velocity variables of the
i-th agent, respectively.
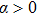
and
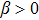
are the coupling strengths.

is the coupling function.
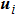
and

are the impulsive control inputs for position and velocity variables, respectively.
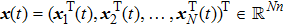
,

.
Definition 4 If for any initial condition
 ,
,
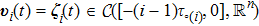 , we have
, we have
then the SLCC of second-order multi-agent systems (
30) is said to be achieved, where the consensus delay

,
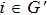
.
To ensure the invariance of the cluster consensus manifold of system (30), the preliminary functions and coupling functions are introduced. Some preliminary functions are defined as
The coupling functions can be given as
Then we have
According to Definition 4, the SLCC errors of second-order multi-agent systems (30) are defined as
 ,
,
 , for
, for
 ,
,
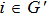 .
.
Based on Assumption 1, the impulsive controllers can be designed as
where

,

are impulsive gain matrices and the constants
cj are defined as

,

, for

and
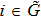
.
Then, for
 , the error systems can be described as
, the error systems can be described as
Similarly, from Assumption 1, for
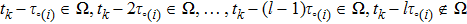 ,
,
 , we have
, we have
Let
 ,
,
 ,
,
and
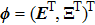
, then the error system can be rewritten as
where
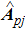
is the rest of block matrix

by deleting its last column and last row,

,
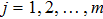
.
Theorem 2 If there exist real number ρ and
 such that
such that
where
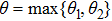
, then the SLCC of second-order multi-agent systems (
30) under delay-dependent impulsive control (
34) can be achieved for any initial conditions.
Proof The Lyapunov function can be defined by
where
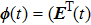
,

.
When
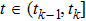 , by applying Lemma 1 and Lemma 2, the derivative of
, by applying Lemma 1 and Lemma 2, the derivative of
 along trajectories of error system (36) can be given by
along trajectories of error system (36) can be given by
Therefore, we have
When
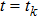
, we obtain
Similarly, for any
 , we have
, we have
Thus, as
 , we have
, we have
It is easy to see that
 as
as
 . Then, we have
. Then, we have
 ,
,
 . Thus, according to Definition 4, the SLCC of second-order multi-agent systems (30) under delay-dependent impulsive control (34) is achieved. This completes the proof.
. Thus, according to Definition 4, the SLCC of second-order multi-agent systems (30) under delay-dependent impulsive control (34) is achieved. This completes the proof.
Remark 6 Compared with the first-order multi-agent systems, the second-order multi-agent systems consider not only the position, but also the velocity. If we set α=1 and β=0, then the second-order multi-agent systems (30) will become the first-order multi-agent systems (5). Note that we cannot derive Theorem 1 from Theorem 2 by setting α=1 and β=0, which means that the SLCCs on first-order multi-agent systems and second-order multi-agent systems are essentially different.
5. Numerical examplesIn this section, without loss of generality, we will consider the first-order and second-order multi-agent systems with six agents. Two fixed directed topology graphs are shown in Fig. 1. And two numerical examples are given to verify our theoretical results.
Example 1 Consider the first-order multi-agent systems with 6 agents and
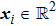 . The directed topology graph of system (5) is depicted in Fig. 1(a). Divide the set of agents
. The directed topology graph of system (5) is depicted in Fig. 1(a). Divide the set of agents
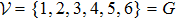 into m = 2 clusters; i.e., G1={1,2,3} and G2={4,5,6}. The coupling matrix can be described as
into m = 2 clusters; i.e., G1={1,2,3} and G2={4,5,6}. The coupling matrix can be described as
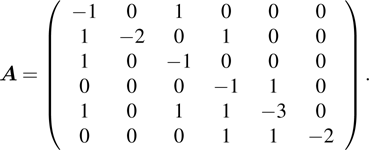 | |
The impulsive gain matrix can be given by
 . Let the consensus delay of the first cluster be τ1=0.7 and that of the second cluster be τ2=0.1. Without loss of generality, the initial values
. Let the consensus delay of the first cluster be τ1=0.7 and that of the second cluster be τ2=0.1. Without loss of generality, the initial values
 are randomly chosen in
are randomly chosen in
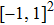 . By a simple calculation, we can obtain a feasible solution with ρ=−0.5419, θ=1.9600, and the average impulsive interval
. By a simple calculation, we can obtain a feasible solution with ρ=−0.5419, θ=1.9600, and the average impulsive interval
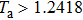 , which satisfies the conditions of Theorem 1. Choose Ta=1.5 and N0=10. Figure 2 describes the state variables of the agents under coupling functions (8) and delay-dependent impulsive controllers (10), which means that system (5) achieves SLCC. Note that
, which satisfies the conditions of Theorem 1. Choose Ta=1.5 and N0=10. Figure 2 describes the state variables of the agents under coupling functions (8) and delay-dependent impulsive controllers (10), which means that system (5) achieves SLCC. Note that
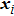 converge to constants as
converge to constants as
 because the first-order multi-agent system (5) is a linear system. It is observed that the error systems converge to 0 as
because the first-order multi-agent system (5) is a linear system. It is observed that the error systems converge to 0 as
 in Fig. 3. Hence, this verifies the correctness of Theorem 1 very well.
in Fig. 3. Hence, this verifies the correctness of Theorem 1 very well.
Example 2 Next, consider the second-order multi-agent systems with 8 agents, where position variable
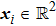 and velocity variable
and velocity variable
 . The directed topology graph of system (30) is depicted in Fig. 1(b). Divide the set of agents
. The directed topology graph of system (30) is depicted in Fig. 1(b). Divide the set of agents
 into m = 2 clusters; i.e., G1={1,2,3,4} and G2={5,6,7,8}. The coupling matrix of directed graph
into m = 2 clusters; i.e., G1={1,2,3,4} and G2={5,6,7,8}. The coupling matrix of directed graph
 can be given as
can be given as
In this case, choose the coupling strengths α=3, β=6, and the impulsive gain matrices
 ,
,
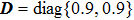 . Let the consensus delay of the first cluster be τ1=0.01 and that of the second cluster be τ2=0.005. By a simple calculation, we can find a feasible solution with ρ=37.3800 and θ=0.1600. Based on Theorem 2, the average impulsive interval should satisfy
. Let the consensus delay of the first cluster be τ1=0.01 and that of the second cluster be τ2=0.005. By a simple calculation, we can find a feasible solution with ρ=37.3800 and θ=0.1600. Based on Theorem 2, the average impulsive interval should satisfy
 . Therefore, we can set Ta=0.04 and N0=10. The trajectories of position variables and velocity variables are presented in Figs. 4 and 5, which show that the system (30) achieves SLCC. The trajectories of the error systems are shown in Figs. 6 and 7. These simulations verify our theoretical results very well.
. Therefore, we can set Ta=0.04 and N0=10. The trajectories of position variables and velocity variables are presented in Figs. 4 and 5, which show that the system (30) achieves SLCC. The trajectories of the error systems are shown in Figs. 6 and 7. These simulations verify our theoretical results very well.
6. ConclusionThis paper focuses on the successive lag cluster consensus of multi-agent systems under impulsive control. According to the SLCC error, we introduce a special impulsive control which depends on the consensus delay. We re able to transform the problem of successive lag consensus with variable consensus delay into cluster consensus; that is, there are different consensus delays in different clusters. Then, we present the application of SLCC on first-order multi-agent systems. By applying the Lyapunov stability theory, we obtain a sufficient condition for the stability of SLCC on first-order multi-agent systems. Moreover, the SLCC of second-order multi-agent systems under delay-dependent impulsive control is also discussed. Finally, we consider two different network topology diagrams. The numerical examples are shown to verify the theoretical results very well.
It is well-known that the noise universally exists in nature. In the near future, we may study the successive lag cluster consensus of multi-agent systems with noise under impulsive control.