Bismuth (Bi) has been widely studied experimentally and theoretically under high pressure due to its complex phase diagram and its abundant pressure-induced polymorphic phases.^[1–20] Previous studies have indicated that bismuth undergoes three pressure-induced structural phase transitions in the pressure range below 10 GPa at room temperature. Under ambient conditions, bismuth is stable in phase I (Bi-I) having a rhombohedral A7-type crystal structure with space group .^[1] The first phase transition occurs at around 2.5 GPa to phase II (Bi-II),^[2] which has a monoclinic structure with space group C12/m1.^[3] Bi-II has a very narrow stability pressure range, and it transforms to the complex phase III (Bi-III) as the pressure increases to 2.7 GPa.^[4] Bi-III has been reported as a composite tetragonal host–guest structure.^[5] Bi-III transforms to phase V (Bi-V) at 7.7 GPa,^[6] which is a body-centered cubic structure shown to be stable up to 222 GPa.^[7] In addition to the static high pressure investigations, shock compression studies of bismuth have also been reported on shock-induced transition and melting.^[8–18] The three structural transitions have been reported in shock compression with the phase transition pressures at 2.7 GPa,^[8] 3.2 GPa,^[15] and 7.0 GPa,^[10] which are different from the results in static compressions. Furthermore, a high temperature and high pressure phase of bismuth (Bi-IV) with an orthorhombic structure has been identified at ∼ 4 GPa and ∼ 500 K.^[19]

Up to now, the pressure-induced structure transformation in bismuth has mainly been studied using static compression in diamond anvil cell (DAC) or shock wave loading. However, the kinetics of a pressure-induced phase transition, e.g., transition pressure and characteristic time, should be related to the pressure loading rate. Recently, the development of dynamic diamond anvil cells (dDAC) with time-resolved synchrotron x-ray diffraction make structural measurement possible under rapid compression with timescales in the order of a millisecond.^[22]

In this paper, we present a study of structural phase transitions in bismuth under rapid compression at room temperature using the fast loading DAC technique with time-resolved synchrotron x-ray diffraction, which has been recently developed at the Beijing Synchrotron Radiation Facility (BSRF). The experimental results show that Bi-I, Bi-II, Bi-III, and Bi-V appear one by one as the pressure increases from ambient pressure to ∼ 12 GPa. There is no change in the phase transition path of bismuth under rapid compression at different compression rates (0.20–183.8 GPa/s) compared with the static high pressure experiments. In the phase transition process from Bi-III to Bi-V, the increasing volume fraction of Bi-V versus pressure generally gives a sigmoidal curve which can be well fitted by a compression-rate-dependent function. The fitting results show that, as the compression rate increases, the activation energy associated with this transformation decreases while the onset transition pressure increases. Moreover, a strong compression rate dependence of over-pressurization occurs under rapid compression, and a formula of over-pressure is defined to quantify over-pressurization.

A symmetric diamond anvil cell equipped with a pair of diamond anvils with a culet diameter of 250 μm was used for the rapid compression experiments. A rhenium (Re) gasket was used with the sample chamber diameter of ∼ 100 μm and pre-indented thickness of ∼ 40 μm. Bismuth sample powder with 99.5% purity (Alfa Aesar) was pressed into a thin slice, and then loaded into the sample chamber. Sodium chloride (NaCl, from Alfa Aesar) was added as the pressure medium to obtain quasi-hydrostatic pressure conditions, as well as the internal pressure marker. After sample loading, the DAC was inserted into a dDAC which was driven by a piezoelectric actuator.

Time-resolved synchrotron x-ray diffraction experiments were carried out using the angle-dispersive diffraction method with a monochromatic x-ray beam wavelength of 0.6199 Å at the 4W2 high pressure station at BSRF. The incident x-ray beam was focused in the horizontal and vertical directions to a 25 × 10 μm² (full width at half maximum (FWHM)) spot on the sample using Kirkpatrick–Baez mirrors.^[21] The two-dimensional diffraction pattern was collected using a PILATUS2 2M area detector with an exposure period of 100 ms and an exposure time of 90 ms for each image.

A function generator and a digital oscilloscope were used for synchronization, triggering, and monitoring the timing between the x-ray detector and the dDAC rapid compression device. We used trapezoid waveforms to trigger the piezoelectric actuator to modulate the rapid compressions in the dDAC, and used pulse waveform to trigger the detector to collect the diffraction patterns. By adjusting the timing of the trigger waveforms of the dDAC and detector, the pressure compression and the x-ray diffraction image collection proceeded simultaneously. The Fit2D program^[23] was used to integrate the diffraction images to obtain intensity versus 2-theta plots. Then the diffraction data were analyzed to index the diffraction peaks by using the Jade (MDI Jade 6) program. The sample pressure was determined from the NaCl (200) diffraction peak in each diffraction image by using the equation of state (EOS) previously reported.^[24] The compression rate of the experiment was estimated by the rising slope of the determined pressure versus time.

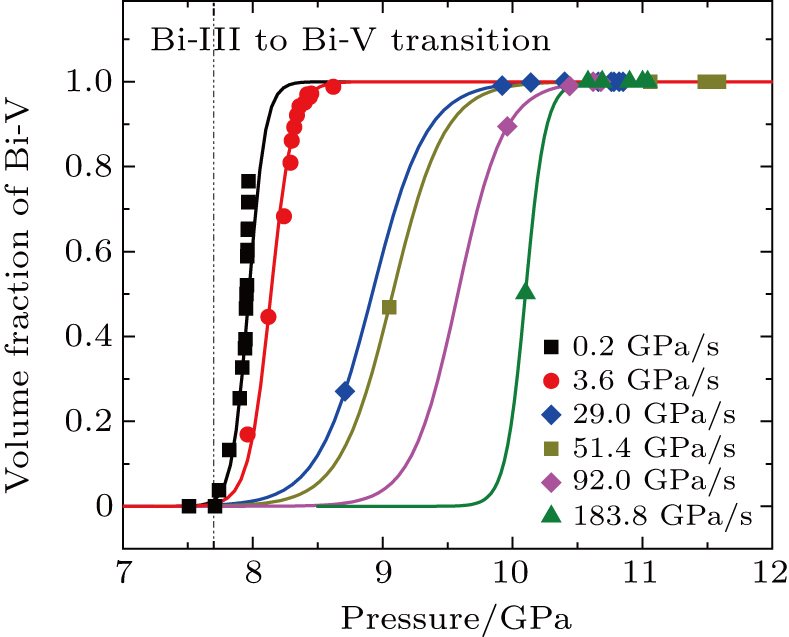
In the case of rapid compression, the volume fraction of product phase during the phase transformation process as a function of pressure can be described by Eq. (1)^[25] which is based on the Johnson–Mehl–Avrami–Kolmogorov (JMAK) equation 1 2 3 4 where x_ex(P) is the extended volume, nucleation rate I(P) and growth rate v(P) are pressure-dependent at a given compression rate k, Q_N and Q_G are the activation energies in the nucleation and growth processes, respectively, ΔG_V is the difference of the Gibbs free energy induced by the volume change associated with the transformation, P₀ is the onset phase transition pressure, n is the growth exponent, k_B is the Boltzmann constant, and T is the room temperature. To the zero-order approximation, we assume that the nucleation rate I(P) and growth rate v(P) change very little with pressure. The equations (1)–(4) are reduced to 5 where 6 Here, A is related to the activation energy at a given compression rate. The dimensionality of the growth n, the so-called Avrami exponent, should be equal to 3 in this study because nuclei form in the grain interior and grow in three dimensions.^[26] The compression rate k can be obtained by fitting the pressure–time data. There are only two parameters A and P₀ in fitting the volume fraction data according to Eq. (5).

Figure 1 shows the pressure dependence of the interplanar distances of Bi under different compression rates. Bi-I is the initial phase before each rapid compression. As the pressure increases, the decreases and transformations of the interplanar distances have been clearly shown in Fig. 1, indicating the structural evolutions of bismuth from phase I, to phase II, to phase III, and then to phase V induced by rapid compressions. In the cases of the compression rates of 92.0 GPa/s and 183.3 GPa/s, Bi-II has not been observed due to the very narrow stability pressure range of phase II and an insufficient time resolution in the experiments. Obviously, no new phase transition sequence occurs during rapid compressions with the compression rate below 183.8 GPa/s.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The interplanar distances of Bi-I (blue), Bi-II (red), Bi-III (green), and Bi-V (purple) against pressure are itemized under different compression rates. Dash-dot lines mark the static onset transition pressures.

The pressure-induced structural phase transition process is studied by tracking the spectral changes in the intensities of the diffraction peaks of the parent phase and the product phase as the pressure increases. Focusing on the phase transition from Bi-III to Bi-V, we obtain the volume fraction of the Bi-V as a function of pressure at each compression rate, as shown in Fig. 2. The volume fraction of the Bi-V at pressure P is defined by f(P) = I₂(P)/(I₁(P)+I₂(P)), where I₁(P) and I₂(P) are the integrated intensity of the diffraction peaks of the Bi-III and Bi-V at P, respectively. As illustrated in Fig. 2, the volume fraction can generally be well fitted using Eq. (5). And the fitting curves provide the details that the resultant parameters, A and P₀, show strong dependence on the compression rate, as shown in Fig. 3.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The volume fractions of Bi-V are plotted as a function of pressure at different compression rates. The solid symbols show the experimental data, and the solid lines are the fitting curves based on Eq. (5). The dashed line is the onset transition pressure across the transition from Bi-III to Bi-V previously reported in static high pressure experiments.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The plot of −ln(A) and P0 as a function of compression rate. The black square symbols show the results of −ln(A), which are related to kinetic barriers at different compression rates. The red circle symbols show the onset transition pressure P0 at each compression rate.

According to Eq. (6), the opposite of the natural logarithm of A (−ln(A)) is positively correlated with the activation energy (Q_N0 + nQ_G0), and can be used to indicate the trend of the energy barrier associated with this transition. The fitting results of −ln(A) as a function of compression rate are shown in Fig. 3, illustrating that the kinetic barrier of this transformation decreases as the compression rate increases.

The fitting results of the onset phase transition pressure P₀ at different compression rates are also plotted in Fig. 3. It can be found that P₀ has a linear relationship with the compression rate k. As the compression rate increases, the onset phase transition pressure increases. This result suggests that a compression-rate-dependent over-pressurization occurs during the phase transition from Bi-III to Bi-V induced by rapid compression, which can also be seen in Fig. 2 as the fitting fraction curve shifts toward the higher pressure direction as the compression rate increases.

The transformation rate equation, well-known as the JMAK rate equation, is often used to describe kinetic processes of phase transitions induced by temperature under heating at given heating rates.^[27–29] Similarly, the differentiation of Eq. (5) results in a transformation rate equation under rapid compression condition 7 where parameter A dependent on k is related to the activation energy associated with this transition, as mentioned above. From Eq. (7), it can be seen that the transformation rate only depends on the pressure (through k) and the transformed fraction. At a given pressure P, the change of transformed fraction in the small range of ΔP can be expressed as 8 Actually, Δf can be treated as a weighting factor for characterizing the contribution of the current pressure to the phase transition. Here, we define the over-pressure P_ov as a weighted average pressure which can be used to quantify over-pressurization. It may be described by 9 where the integration is over the pressure range of the phase transition. As shown in Fig. 4, as the compression rate increases, the over-pressure increases as well as the onset transition pressure.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The influence of compression rate on the over-pressure and onset transition pressure.

In summary, using a dynamic-DAC and time-resolved synchrotron x-ray diffraction, the structural evolution of bismuth induced by rapid compression has been probed with 100 ms time resolution at room temperature. The structural evolutions of bismuth induced by rapid compressions in the rate range from 0.2 GPa/s to 183.3 GPa/s have been observed. The phase transition sequence is the same as that in static high pressure experiments. In the process from Bi-III to Bi-V, the volume fraction of Bi-V versus pressure can be well fitted by a sigmoidal curve. The fitting results show that the activation energy associated with this transformation depends on the compression rate. A strong dependence of over-pressurization on compression rate has been found under rapid compression. In order to quantify the over-pressurization, a formula for over-pressure has been proposed.