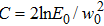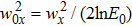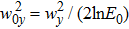Cite this Article
Yin Cheng, Kan Xuefen, Dai Hailang, Shan Minglei, Han Qingbang, Cao Zhuangqi. Propagation dynamics of off-axis noncanonical vortices in a collimated Gaussian beam. Chinese Physics B, 2019, 28(3): 034205  
Permissions
Propagation dynamics of off-axis noncanonical vortices in a collimated Gaussian beam
Yin Cheng1, 2, †, Kan Xuefen1, Dai Hailang2, Shan Minglei1, Han Qingbang1, Cao Zhuangqi2
Jiangsu Key Laboratory of Power Transmission and Distribution Equipment Technology, Hohai University, Changzhou 213022, China
The State Key Laboratory on Fiber Optic Local Area Communication Networks and Advanced Optical Communication Systems, Shanghai JiaoTong University, Shanghai 200240, China

 

† Corresponding author. E-mail: cyin.phys@gmail.com

Project supported by the Fundamental Research Funds for the Central Universities, China (Grant No. 2017B14914), China Postdoctoral Science Foundation (Grant No. 2016M601586), and the National Natural Science Foundation of China (Grant Nos. 11874140 and 11404092).

Abstract

It is widely accepted that an off-axis noncanonical vortex moves across the free-space diffracting Gaussian beam without rotation. But our analysis shows that the vortex swirls a while before it approaches infinite. By neglecting the divergence of the host beam, we focus on this rotation characteristics of the vortices in linear homogeneous media. For the symmetrical host beam, it is found that the vortex moves along an elliptical trajectory, while the topological charge and the angular momentum of the vortex core relative to the beam axis are conserved. For the asymmetrical host beam, the vortex trajectory is rather complicated, since the noncanonical parameter varies as the light propagates, resulting in topological charge inversion. But we find that the vortices are always confined in a rectangular area, and the rotation direction is determined by the topological charge.

PACS: 42.50.Tx;47.32.C-
Keyword:noncanonical optical vortex;topological charge inversion
1. Introduction

There has been considerable interest on the phase singularities nested in wave fronts, i.e., the optical vortices, which are surrounded by wave fields with helicoidal phase structures and may carry the orbital angular momentum.[1] The study on the optical vortices is important both fundamentally and practically, whilst the potential applications include laser trapping,[2] optical data storage,[3] optical information processing,[4] and so on. Optical vortices are also intriguing because they behave in some degree as “particles” in the host beam, and exhibit rich propagation dynamics, while the paths of the vortices can be twisted, looped, and even knotted.[5] When the vortex trajectory is parallel to the wavevector k of the host beam, the resulted beam has helicoidal wave fronts; the situation would be much complicate when the vortex lines take other forms. Consequently, the dynamics of the vortices have been extensively investigated, especially in nonlinear systems,[6–9] including Kerr-type media,[10] cubic–quintic saturating nonlinearity,[11] and nonlocal nonlinear media.[12,13] Even in the linear regime, the free-space propagation of optical vortices may present unusual dynamical properties. For example, identical vortices are found to orbit each other and diffract in a linear medium.[14] Additional vortices can be created when the off-axis vortex is interacted with host beams with dislocation surfaces, e.g., Laguerre–Gaussian (LG) beams.[15] Passing through a cylindrical lens, the noncanonical evolution of an initially canonical vortex leads to a competition between the angular momentum eigenmodes, and results in the inversion of the topological charge.[16] Gouy phase is applied to explain the rotation of multi off-axis vortices that are generated in the collinear superposition of LG beams.[17] The propagation dynamics of both axial[18] and off-axis[19] noncanonical vortices have been investigated. It is pointed out that an off-axis noncanonical vortex moves across a background Gaussian beam without rotation.[14,19]

This paper focuses on the propagation dynamics of a single off-axis vortex in Gaussian beam with or without cylindrical symmetry. It is found that the vortex swirls a while before it approaches infinite, which is mainly due to the divergence of the host beam. By neglecting the divergence, an elliptical orbit around the beam axis can be derived analytically for the symmetrical beam. On the contrary, the vortex trajectory is much complicate in the background of asymmetrical Gaussian beam due to the inversion of the topological charge. In both cases, the vortices are confined in a rectangular area, which is specified by the noncanonical parameter à and the ellipticity of the host beam. To treat the swirling vortex as a “particle”, we define a particle-like angular momentum Lp of the vortex center relative to the beam axis. It turns out that the Lp is conserved only in the symmetrical host beam. Numerical simulation suggests that in the case of asymmetrical beams, the moment of inertia of the off-axis vortex can be roughly approximated as |Re(Ã) |r2. This work may be useful in the exact control over the off-axis vortex position and find application in areas such as optical manipulation, beam shaping, etc.

2. Vortex propagation in symmetric host beam

Let us assume a complex scale optical field E(x,y,z) with a noncanonical vortex embedded in it, which can be cast into

where F(x,y,z) is the host beam, and
describes a vortex of topological charge one, whose sign is the same as that of the real part of the noncanonical parameter à = Ar +i Ai. When à = ± 1, this vortex reduces to a canonical, i.e., symmetrical vortex, since x±iy = rexp(±iθ). In Fig. 1, we show a few examples, where arbitrary units are applied.

Fig. 1. Examples of canonical (Ã = 1, x1 = 0.5, y1 = 0.5, above) and noncanonical (Ã = 1 + i, x1 = 0.5, y1 = 0.5, below) vortices as V = (x–x1) + iÃ(y–y1) nested in a symmetrical Gaussian beam.

Two important expressions can be derived from the paraxial wave equation in normalized units , which determine the propagation dynamics and the variation of the noncanonical parameter[19]

where L1 = ∂ / ∂x+iÃ∂/∂y, and L2 = iÃ∂/∂x–∂/∂y. Consider a symmetrical Gaussian beam propagating in a linear homogeneous medium
where ρ2 = x2 + y2, w0 is the waist radius, and Z0 is the Rayleigh distance. In view of Eqs. (4) and (5), it shows that à is constant. Substituting Eq. (5) into Eq. (3), we obtain the following equation:
which describes the propagation trajectory of the vortex position (x1,y1). For the rest of the paper, the initial position of the vortex is denote as (x10,y10). Equation (5) confirms that if the initial position of the vortex is at the center of the beam, then this vortex would not move during propagation. Figure 2 shows the numerically simulated trajectories of several off-axis vortices, where the parameters are w0 = 1, Z0 = 10, and à = 2. It is clear that these vortices will eventually move to infinity, but the obtained results are slightly different from those in Ref. [19]. The reference predicted that the vortex leaves the host beam in a straight line, but figure 2 shows that the vortices move in a spiral way. The difference is due to the specific approximation used in Ref. [19]. Careful investigation shows that the initial direction of motion of the vortices in Fig. 2 is perpendicular to the direction of the sloping field.[14] If the real part of à is negative, the projections of the vortex trajectories onto the transverse plane will be a large clockwise rotation. This paper will focus on this spiraling property of the off-axis vortex in the linear homogeneous medium, so the divergence of the host beam will be ignored.

Fig. 2. Calculated propagation dynamics of several single off-axis vortices with different initial positions (x10,y10) in a host Gaussian beam. The colored dashed lines are the trajectories of the transverse motion of the optical vortices. Arbitrary units are applied.

Assume that Z0 ≫ z, so the term 1 + iz/Z0 in Eq. (5) can be omitted, which can be recast into the well-known form

where wx = wy = w0 for a symmetrical Gaussian beam, and wx ≠ wy for the asymmetrical case. First, we consider the simple symmetrical case, where equation (4) yields dÃ/dz = 0, indicating that the noncanonical parameter is invariant. Then equation (6) can be split into
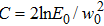
where the parameter . Consider the simple case of Ai = 0, it immediately follows that the vortex trajectory in the transverse plane is an ellipse, while the semi-major and semi-minor axes coincide with the x and y axes, respectively. Consequently, we can write the elliptical trajectory as
where a and b are the semi-major and semi-minor axes, respectively. Combining Eqs. (8) and (9), it is not difficult to derive
As can be seen from Eq. (10), the rotation speed of the vortex is determined by the waist radius of the beam, and the rotation direction depends on the sign of Ar. And the absolute value of the noncanonical parameter à is equal to the ratio of the major and the minor axes of the ellipse.

For the more general case of Ai ≠ 0, it can be proved that the vortex trajectory is still an ellipse, whose major axis does not need to overlap with the x or y axis. Set the angle between the a axis and the x axis to be ϕ, then we can use a different set of coordinate system (x′,y′), which is related to the original (x,y) by a counter-clockwise rotation ϕ. In the new coordinates, the trajectory is

where
By combining the two equations above, it is not difficult to derive the vortex trajectory in the original coordinate system as
Thus, the trajectory can be solved analytically as follows:
Now we have analytically solved the propagation trajectory of an off-axis vortex, with arbitrary complex noncanonical parameters. Figure 3 gives a concrete example of the dynamics of the rotating vortex around the beam center, whilst the field distribution of the Gaussian beam varies accordingly at different transverse planes. If the host Gaussian beam is well collimated, i.e., Z0 ≫ 0, it is possible to observe such rotation before the vortex leaves the beam.

Fig. 3. Elliptical orbit (black line) of noncanonical vortex embedded in a Gaussian beam, where the parameters are Ar = –1.5, Ai = 2, w0 = 1, E0 = e2, and (x10,y10) = (0.8,0), all the quantities are presented in arbitrary units.

It is interesting to note that there is a common rule related to the vortex trajectory, which still holds even when the host beam becomes asymmetrical. As can be seen from Fig. 4, the elliptical orbits of the vortices locate in rectangular regions of |x1|< xmax and |y1|< ymax. Now we will calculate the ratio between xmax and ymax via Eq. (13)

Substituting Eq. (14) into Eq. (15), and through purely algebraic process, yields a surprisingly simple result
Figure 4 plots the numerical simulated projections of the vortex trajectory onto the transverse plane, where the initial positions of the vortices are set at (0,0.8). By varying the phase ϕA, and keeping the |Ã| constant, the elliptical trajectories vary differently, but the values of xmax/ymax are invariant.

Fig. 4. The xmax/ymax of optical vortices in a symmetrical Gaussian beam is determined solely by the amplitude of parameter Ã. The parameters in arbitrary units are (x1,0,y1,0) = (0,0.8), Ã = 1.5eiϕA, and w0 = 1.

Because the optical vortex behaves in some degree as a particle, we can define an angular momentum of the rotating vortex core relative to the axis of the host beam. Note that this angular momentum is different from the orbit angular momentum carried by the wavefront of the vortex or the whole beam. So we can define the angular momentum of the particle-like vortex core as

where ez is the unit vector along the z-axis. Inserting Eq. (13) into Eq. (17) yields
And in view of Eq. (14), it is clear that the angular momentum is completely determined by à and the initial position (x10,y10). Equation (18) confirms that Lvc is invariant for the symmetrical host beam, since à is constant.

3. Vortex propagation in asymmetric host beam

From now on, we will consider the case of asymmetrical beam, which is given by Eq. (7) with wx ≠ wy. Equation (4) turns into

which follows
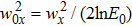
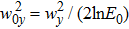
where . In the asymmetric host beam, Ã rotates in the complex plane according to Eq. (20), whilst the topological charge has the same sign as the real part of Ã, so the topological charge switches between positive and negative as the beam propagates, this is known as the effect of topological charge inversion. Assuming Ã(0) = |Ã|exp(iϕA), , , we can derive the vortex trajectory in the asymmetrical beam as
where
It is interesting to note that the determinant of the matrix is
Equations (20)–(22) describe how the vortex moves as the beam propagates and how the topological charge varies. For illustration, figure 5 simulates the dynamics of an off-axis vortex embedded in an asymmetrical beam, the parameters are (x10,y10) = (1,0.5), wx = 1, wy = 0.8, and Ã(0) = 1+i. It is clear that the vortex simultaneously rotates at a constant speed and moves along a complicate trajectory.

Fig. 5. Calculated propagation dynamics of an off-axis vortex in an asymmetrical Gaussian beam, where the red line denotes the trajectory of (x1,y1) and the black arrows denote the direction of à in the complex plane

There is no need to go to the details of the trajectory, which is too complicate. Instead, let us exam if the vortex trajectory is confined in a finite space in the transverse plane. We can calculate the acceleration of the vortex core, which can be derived as

where
It can be proved that , and the case of symmetrical host beam falls into the special case of kA = 0. Let the same vortex in Fig. 5 propagate for a longer distance 0 < z < 30. Figure 6 plots the projection of its trajectory on the transverse plane. It is obvious that the trajectory is still confined in a rectangle, which proves that the off-axis vortex would not leave the beam if the divergence of the beam is ignored. Imagine that the vortex is at the corner of the rectangle, then both derivatives dx1 / dz and dy1/dz should approach zero. Inserting this assumption into Eq. (21), we can derive
which is verified by the numerical results in Fig. 6. And it is not difficult to see that equation (16) is only a special case of Eq. (26) when wx = wy.

Fig. 6. Trajectory of transverse motion of optical vortex in an asymmetrical Gaussian beam, which is obviously confined in a rectangle.

Finally, we consider the angular momentum of the particle-like vortex center relative to the center of the host beam based on Eq. (17), which is shown in Fig. 7. For comparison, we plot the real part of the noncanonical parameter Re(Ã), whose sign defines the topological charge of this vortex. It is found that Re(Ã) has the same period as Lvc, and the latter is no longer invariant for the asymmetrical host beam.

Fig. 7. Comparisons of the real part of the noncanonical parameter Re(Ã), the angular momentum Lvc defined by Eq. (17), and the product of Re(Ã) ×|r|2 as a function of the propagation distance z.

In order to study the physics behind, we further calculate the product of Re(Ã)× |r|2, it turns out that the curves of Lvc and Re(Ã)×|r|2 should be intimately related. It is interesting since these two curves are obtained via quite different equations. The fact that Lvc in an asymmetric host beam can be both positive and negative shows the rotation direction of the off-axis vortex is variable. Equation (21) connects the velocity v = (vx,vy) with the vortex core position r = (x1,y1). It is not difficult to verify that if vx y1 –vy x1 >0, the vortex rotates clockwise, and vice versa. Inserting Eq. (21) into the criteria, it turns out that the rotation direction is determined again by the sign of Re(Ã), which fits well with the simulated results in Fig. 7. As Re(Ã) is negative, the topological charge is −1, the vortex rotates clockwise. It should be note that this rule holds for both symmetric and asymmetric cases (see Fig. 3). Two hypotheses are available here.

(I) If the vortex is treated as a particle, then the term |Re(Ã)|r2 can be used as a rough approximation of the moment of inertia I = mr2, where the effective mass is approximated as |Re(Ã)|. In a symmetric host beam, the effective mass is constant.

(II) The topological charge inversion is the physics behind the rather complicate propagation property of a noncanonical vortex in an asymmetric host beam, which leads to the frequent variation of rotation direction.

4. Conclusion

We analytically investigate the propagation dynamics of a single off-axis vortex nested in both symmetrical and asymmetrical host beams in details, where the vortex swirls around the beam axis if the divergence is ignored. For the symmetrical case, a simple elliptical orbit in the transverse plane can be defined, whilst the topological charge and the angular momentum Lvc of the rotating vortex center are invariant as the beam propagates. For the asymmetrical background beam, the trajectory of the vortex is rather complicate, since the noncanonical parameter varies simultaneously. The topological charge and the angular momentum Lvc relative to the beam axis are not conserved. But in both cases, the vortex is always confined in a rectangular area and the rotation direction is determined by the sign of the topological charge.

Reference
[1] Allen L Barnett S M Padgett M J 2003 Optical Angular Momentum Bristol Institute of Physics Publishing
[2] Gecevicius M Drevinskas R Beresna M Kazansky P G 2014 Appl. Phys. Lett. 104 231110
[3] Yan Y Yue Y Huang H Ren Y Ahmed N Tur M Dolinar S Willner A 2013 Opt. Lett. 38 3930
[4] Zhang M Jia P Li Y Lei T Li Z Yuan X 2015 Chin. Opt. Lett. 13 100502
[5] Dennis M R King R P Jack B O’holleran K Padgett M J 2010 Nat. Phys. 6 118
[6] Desyatnikov A S Kivshar Y S Torner L 2005 Prog. Opt. 47 291
[7] Terriza G M Petrov D V Recolons J Torner L 2002 Opt. Lett. 27 625
[8] Reyna A S De C B 2016 Phys. Rev. 93 013843
[9] Toda Y Honda S Morita R 2010 Opt. Exp. 18 17796
[10] Lenzini F Residori S Arecchi F T Bortolozzo U 2011 Phys. Rev. 84 061801
[11] Berezhiani V I Skarka V Aleksić N B 2001 Phys. Rev. 64 057601
[12] Buccoliero D Desyatnikov A S Krolikowski W Kivshar Yu S 2007 Phys. Rev. Lett. 98 053901
[13] Skupin S Grech M Królikowski W 2008 Opt. Exp. 16 9118
[14] Rozas D Law C T Swartzlander G A Jr. 1997 J. Opt. Soc. Am. 14 3054
[15] Flossmann F Schwarz U T Maier M 2005 Opt. Comm. 250 218
[16] Molina-Terriza G Recolons J Torres J P Torner L Wright E M 2001 Phys. Rev. Lett. 87 023902
[17] Baumann S M Kalb D M MacMillan L H Galvez E J 2009 Opt. Exp. 17 9818
[18] Singh R P Chowdhury S R 2003 J. Opt. Soc. Am. 20 573
[19] Terriza G M Wright E M Torner L 2001 Opt. Lett. 26 163