† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. U1632275), the National Key R&D Program of China (Grant Nos. 2017YFA0303100 and 2016YFA0300202), and the Science Challenge Project of China (Grant No. TZ2016004).
Heavy fermion materials are prototypical strongly correlated electron systems, where the strong electron–electron interactions lead to a wide range of novel phenomena and emergent phases of matter. Due to the low energy scales, the relative strengths of the Ruderman–Kittel–Kasuya–Yosida (RKKY) and Kondo interactions can often be readily tuned by non-thermal control parameters such as pressure, doping, or applied magnetic fields, which can give rise to quantum criticality and unconventional superconductivity. Here we provide a brief overview of research into heavy fermion materials in high magnetic fields, focussing on three main areas. Firstly we review the use of magnetic fields as a tuning parameter, and in particular the ability to realize different varieties of quantum critical behaviors. We then discuss the properties of heavy fermion superconductors in magnetic fields, where experiments in applied fields can reveal the nature of the order parameter, and induce new novel phenomena. Finally we report recent studies of topological Kondo systems, including topological Kondo insulators and Kondo–Weyl semimetals. Here experiments in magnetic fields can be used to probe the topologically non-trivial Fermi surface, as well as related field-induced phenomena such as the chiral anomaly and topological Hall effect.
Heavy fermion compounds are canonical examples of systems in which there are strong electron–electron correlations. These are intermetallic compounds containing certain rare earth atoms with unpaired f-electrons, typically Ce, Pr, Yb, U, etc. While in the isolated case, the f-electron shell is localized to the atoms, in heavy fermion materials there is hybridization between the f-electrons and the conduction electrons via the Kondo interaction.[1] This favors the formation of a Kondo singlet at low temperatures, where the f-electron spin is screened by the conduction electrons.
In heavy fermion materials, the effects of a single f-electron cannot be considered alone, but the arrangement of atoms into a lattice must be taken into account.[1,2] In these systems, two competing interactions need to be considered, the Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction which leads to the ordering of f-electron moments,[3–5] and the Kondo interaction which leads to a non-magnetic ground state. In the Doniach model, the relative strengths of these interactions are tuned by the same coupling constant J, leading to magnetic order for weak coupling.[6] As J is increased, the Kondo interaction eventually gets stronger more rapidly than the RKKY interaction, leading to the suppression of the magnetic order. The ordering temperature can often be reduced to zero at a quantum critical point, where quantum rather than thermal fluctuations drive the properties, leading to unusual phenomena such as non-Fermi liquid behavior, unconventional superconductivity, or other novel phases. The energy scales of heavy fermion systems are generally low and therefore many materials can be tuned through the Doniach phase diagram using various non-thermal parameters such as pressure, doping, or applied magnetic fields.[7,8]
Experiments in high magnetic fields have been very important for understanding the behavior of heavy fermion systems, for instance:
(i) Field as a tuning parameter. Along with pressure and doping, magnetic fields have been used to tune heavy fermion systems. In general, a sufficiently large magnetic field will destroy the Kondo effect, breaking up the Kondo singlets. However, there are examples where field can tune the system to suppress magnetic order, leading to quantum critical behavior. One notable example is YbRh2Si2, where the field-induced quantum critical point is believed to be an unconventional local type at which the Kondo effect is destroyed.[9,10]
(ii) Probing quantum criticality via Fermi surface measurements. One of the notable effects of the Kondo effect in heavy fermion systems is that at low temperatures there is often a reconstruction of the Fermi surface, where the electronic bands pick up a very large effective mass. An important experimental method for probing the Fermi surface is via the de-Haas van-Alphen effect, where the periodicity of the quantum oscillations corresponds to the extremal cross sectional areas of the Fermi surface, and their temperature dependence gives the effective quasiparticle mass. For heavy fermion systems, a consequence of the greatly enhanced effective quasiparticle masses is that characterizing the Fermi surface requires much larger magnetic fields, as well as lower temperatures. There is particular interest in looking at how the Fermi surface is affected as a function of tuning parameters such as field or pressure. It has been proposed that quantum critical points can be classified as either conventional spin density wave (SDW) types or unconventional local types depending on how the Fermi surface changes crossing the quantum critical point at zero temperature.[11–13] At a local quantum critical point, the Kondo effect breaks down and therefore there is a sudden change from a large Fermi surface involving the f-electrons to a small Fermi surface where the f-electrons are fully localized.
(iii) Topological heavy fermion systems. Topological condensed matter systems have been much studied after the discovery that the electronic structures of many materials can be classified as topologically non-trivial. In the case of topological insulators, this implies that even if there is insulating behavior in the bulk, the surface must conduct. The material SmB6 has attracted considerable attention, since it has been proposed to be a topological Kondo insulator, where the gap in the topological band structure opens due to the hybridization between the conduction and f electrons.[14] Measurements in field have been very important for probing the fascinating properties. For instance, despite the apparent bulk insulating state, quantum oscillations have been observed in SmB6 and there has been considerable debate over whether these originate from the conducting surface states[15] or if they are a bulk property.[16,17] Furthermore, field-based thermodynamic and transport measurements have been useful to confirm the presence of conducting surface states,[18–20] as well as to exclude the presence of bulk excitations.[21] Meanwhile heavy fermion systems with gapless topological states have also become of particular interest recently, specifically those which may host Dirac or Weyl points, where there is a linear band crossing with excitations which can be described as Dirac or Weyl fermions.[23,24] High field measurements are vital for studying topological correlated systems. In particular, quantum oscillations are an important tool for revealing the band topology, where an analysis of the field dependence of the Landau indices can reveal whether there is a non-trivial Berry phase.[24–27] Furthermore, systems with Dirac or Weyl fermions exhibit unusual magnetotransport properties, where a negative magnetoresistance when the field and current are parallel is a signature of the chiral anomaly in Weyl fermion systems.[28–32]
Heavy fermion materials can often be tuned by various parameters such as pressure, doping, or magnetic fields. A schematic phase diagram for Ce-based heavy fermion systems under pressure is displayed in Fig.
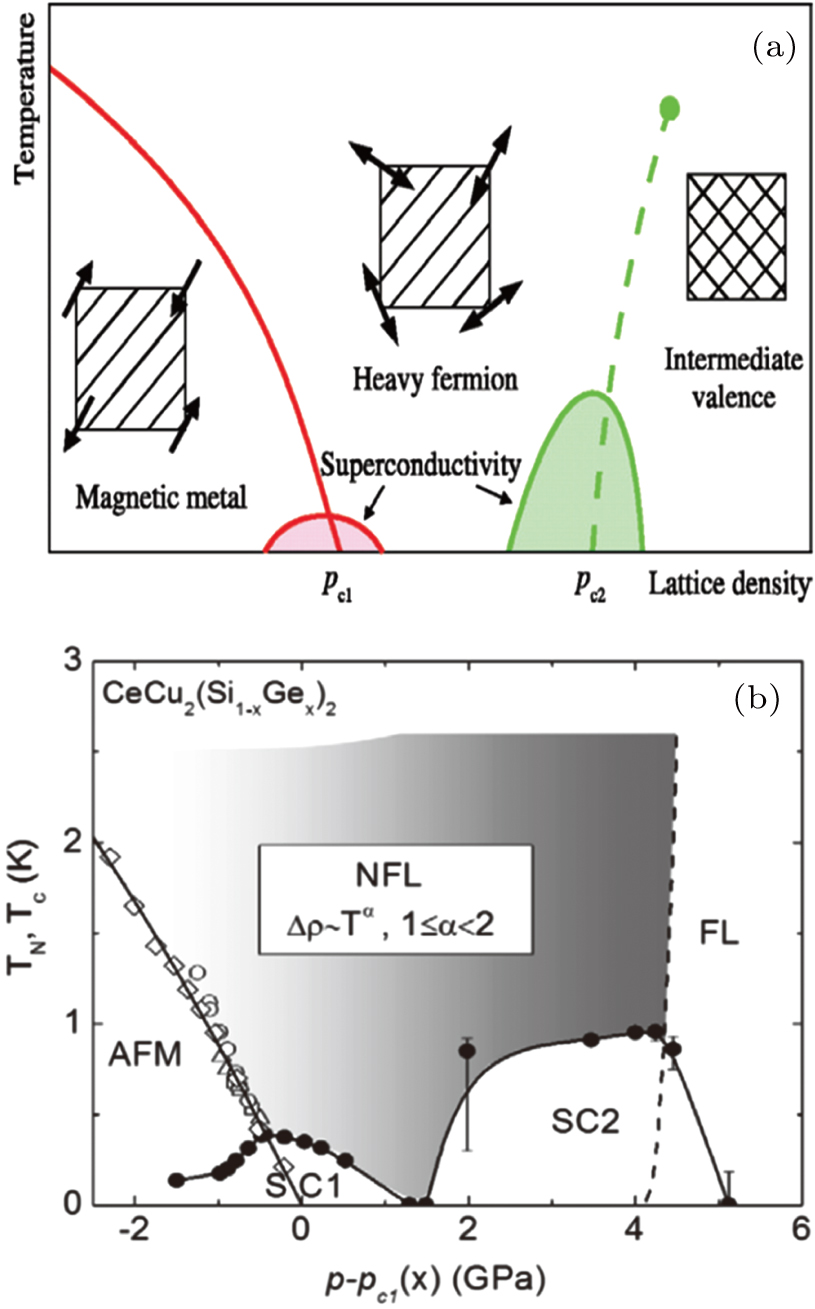 | Fig. 1. (a) A schematic temperature–pressure phase diagram for Ce-based heavy fermion systems under pressure. Reprinted from Yuan et al., Ref. [33]. Copyright 2003 AAAS. (b) Temperature–pressure phase diagram of CeCu2(Si1−xGex)2 reproduced with permission from Yuan et al., Ref. [34]. Copyright 2006 by the American Physical Society. |
One of the richest sources of novel physics in heavy fermion compounds has been the CenTmIn3n+2m (T = transition metal) series of compounds. CeIn3 is a cubic compound which orders antiferromagnetically at TN = 10.2 K.[36] The magnetic order is suppressed by applying pressure and TN reaches zero at a critical pressure of around pc = 2.6 GPa. In this region of the phase diagram, there is a dome of superconductivity with a maximum Tc less than 0.3 K.[37] Following on from this, the CeTIn5 (T = Co, Ir, or Rh) family of compounds were discovered, where layers of CeIn3 are interspersed with TIn2, leading to an overall much more two-dimensional layered structure.[38–40] At ambient pressure, both CeCoIn5 and CeIrIn5 are superconductors with respective bulk Tc values of 2.2 K and 0.4 K, while CeRhIn5 is an antiferromagnet with TN = 3.8 K. The temperature–pressure phase diagram of CeRhIn5 is displayed in Fig.
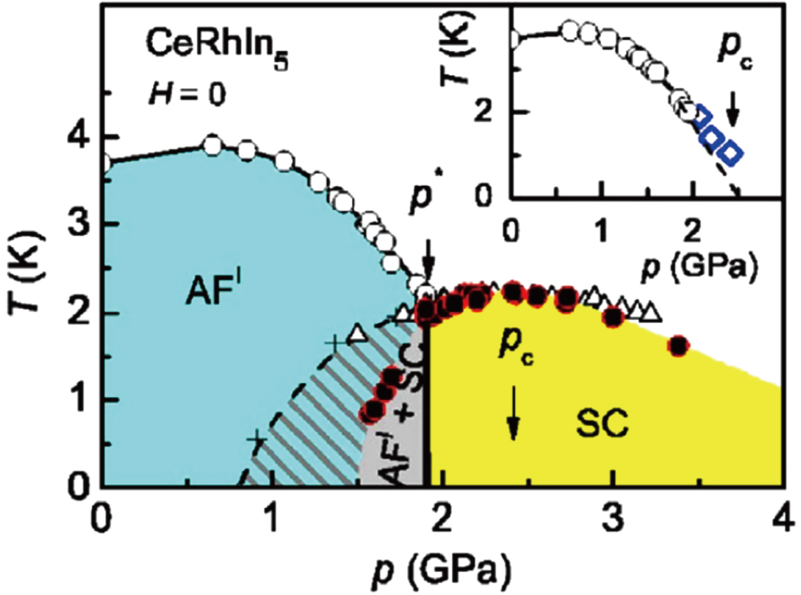 | Fig. 2. Temperature–pressure phase diagram of CeRhIn5 reproduced with permission from Knebel et al., Ref. [41]. Copyright 2006 by the American Physical Society. The antiferromagnetism (AF) is suppressed by pressure until p* where the AF dome meets the superconducting (SC) dome. The quantum critical point pc lies at higher pressure within the SC dome. |
Meanwhile the Ce2TIn8 (T = Co, Pd or Rh) series are another structural variant which also show either superconductivity at ambient pressure or antiferromagnetism with pressure induced superconductivity.[43–45]
As a result, the CenTmIn3n+2m families of compounds have been very important for studying heavy fermion behavior, magnetism, superconductivity, and the interplay between all of these phenomena. Furthermore, measurements under high applied magnetic fields have been vital for understanding many of the properties displayed in these materials. Below we give an overview of some of the results elucidated from such measurements under field.
A particular interest for studies of the CeTIn5 materials has been to uncover how the Fermi surface evolves as the various interactions are tuned. CeRhIn5 is different from both CeCoIn5 and CeIrIn5 in that at ambient pressure there is antiferromagnetic order, which indicates the dominance of the RKKY interaction and a weaker Kondo effect in CeRhIn5. This is consistent with studies of the Fermi surface which show that the 4f electrons are well localized in CeRhIn5, but in CeCoIn5 and CeIrIn5 they are itinerant and contribute to the Fermi surface.[46–48] It is therefore said that CeRhIn5 has a small Fermi surface, while the other two materials have large Fermi surfaces. It was found that in CeRhIn5 at the quantum critical point pc = 2.3 GPa, where antiferromagnetism is suppressed (Fig.
It was therefore desirable to measure the effects of tuning CeRhIn5 using high magnetic fields. This allows for a comparison between the uses of pressure and field as tuning parameters, and the robustness of the magnetism to applied field allows the change of Fermi surface as a function of field to be probed in the magnetic state.
The temperature–field phase diagram is displayed in Fig.
 | Fig. 3. (a) Magnetic field dependence of the heat capacity of CeRhIn5 at various temperatures when the field is along the c-axis. (b) Field–temperature phase diagram of CeRhIn5 for fields along the a- and c-axes. AF and P denote antiferromagnetism and paramagnetism, respectively, while the subscripts mark a small (S) or large (L) Fermi surface. Reproduced from Jiao et al., Ref. [48]. |
Moreover, a clear reconstruction of the Fermi surface is found upon increasing the field, but in this instance it occurs well below the quantum critical point at B* = 30 T, deep inside the antiferromagnetic state. This is clearly illustrated in Fig.
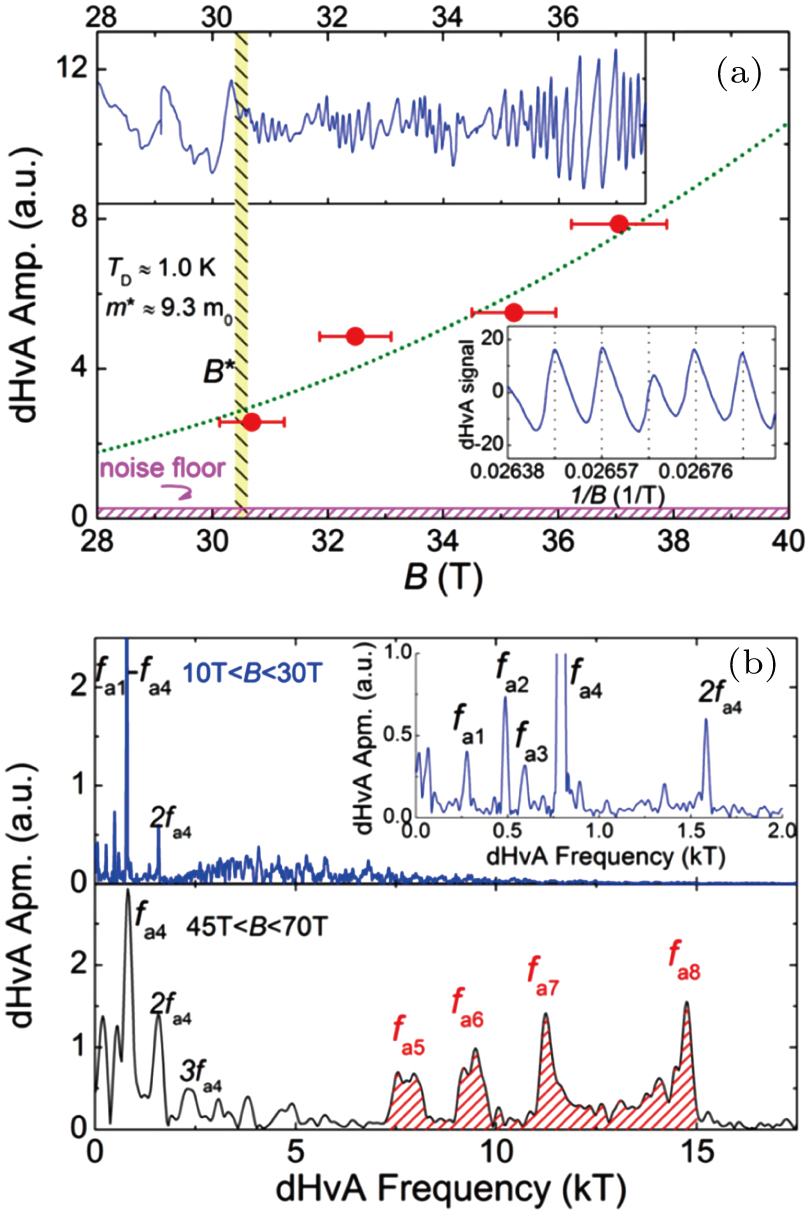 | Fig. 4. (a) dHvA measurements of CeRhIn5 at high fields parallel to the a-axis performed using a piezo-cantilever in a hybrid magnet up to 45 T. The main panel shows the field dependence of the dHvA amplitude of one of the new frequencies above B*. The inset at the top shows the oscillations after subtracting the background while the 1/B dependence is shown in the lower inset. (b) The Fourier transforms of the dHvA data for a field window below (10 T <B < 30 T) and above (45 T< B< 70 T) B*. Both reproduced from from Jiao et al., Ref. [48]. |
 | Fig. 5. A comparison between the fast Fourier transforms of the dHvA spectra of (a) CeRhIn5 at B >B* and B < B*, (b) CeRhIn5 at B < B* and LaRhIn5 from Ref. [41], and (c) CeRhIn5 at B >B* and CeCoIn5 from Ref. [50]. All reproduced from Jiao et al., Ref. [51]. |
 | Fig. 6. The Hall coefficient of CeRhIn5 as a function of field applied parallel to the c-axis, reproduced from Jiao et al., Ref. [48]. |
The observation of a field induced reconstruction of the Fermi surface within the antiferromagnetic state is markedly different to that when pressure is applied, where the Fermi surface reconstruction occurs at the quantum critical point. This indicates that the field induced quantum critical point is of the conventional SDW-type, while the pressure induced quantum critical point is the unconventional local type. The possibility of two different types of QCP found from tuning the same material with two different parameters needs to be explored further, in particular to find whether QCPs can be universally classified.
Compared to the CeTIn5 materials, the Ce2TIn8 family has been much less frequently studied, but the presence of superconductivity in two members at ambient pressure makes them an interesting topic for study. Ce2PdIn8 is one of these materials, displaying superconductivity at Tc = 0.68 K.[45] A further interesting feature is that an applied magnetic field is a good tuning parameter, and evidence was found for a field induced quantum critical point.[53] At zero-field, a superconducting transition is observed in resistivity measurements, which is suppressed as a field is applied.
For fields greater than around 2.4 T, no superconducting transition is found down to 50 mK and the temperature dependence of the resistivity is linear. This indicates the presence of non-Fermi liquid behavior, instead of the ∼ T2 dependence of Fermi liquid theory. Meanwhile, at higher fields, the Fermi liquid behavior is again observed and the temperature below which the ∼ T2 dependence is found (TFL) increases with increasing field, as displayed in the phase diagram in Fig.
 | Fig. 7. Field–temperature phase diagram of Ce2PdIn8 obtained from resistivity measurements. The superconducting (SC), non-Fermi liquid (NFL), and Fermi liquid (FL) regions are all labeled. Figure reproduced from Dong et al., Ref. [53]. |
One particularly promising avenue for exploring the multiple types of QCP is to look for highly frustrated heavy fermion systems, since this has been proposed to promote the unconventional local QCP scenario.[11–13] In a frustrated system, all contributions to the potential energy cannot be simultaneously minimized and two basic effects that introduce frustration to a system are lattice geometric frustration[56] and frustration due to irreconcilable exchange interactions.[57] For example, frustration in magnetic systems arises when the spin configurations cannot be optimized to minimize all the spin interaction energies. In a general heavy fermion phase diagram, besides tuning the hybridization strength between localized moments and the conduction electrons, frustration can add another dimension to the phase diagram that drives the system into intriguing emergent states, as illustrated in Fig.
 | Fig. 8. Generic global phase diagram displaying the combined effects of Kondo coupling (K) and magnetic frustration, or quantum zero-point motion (Q), reproduced with permission from Custers et al., Ref. [60]. Copyright 2010 by the American Physical Society. |
A good candidate for studying frustration is the heavy fermion compound CePdAl with a distorted Kagome lattice.[61] By fitting six inequivalent nuclear Bragg peaks and thirteen inequivalent magnetic Bragg peaks obtained by powder neutron diffraction,[62] it was concluded that CePdAl is a partially frustrated system in which only two thirds of the Ce moments form long-range antiferromagnetic order with a Neel temperature TN = 2.7 K, while the other one third of the Ce moments are disordered due to geometric frustration. This magnetic structure is in agreement with a group theoretical analysis.[62]
For the heavy fermion compound CePdAl, the frustrated moments are screened leading to a heavy fermion state at low temperatures and the intersite correlations between the frustrated moments are likely to be removed, which is supported by neutron scattering[62] and NMR[63] measurements. Upon applying a magnetic field, the Neel temperature is smoothly suppressed initially but goes through several metamagnetic transitions to AF2 and AF3 phases, in the field range of 3.2–4.0 T as shown in Fig.
 | Fig. 9. Magnetic phase diagram of CePdAl for B ∥ c obtained from measurements of different properties. The subscript i for αi and λi denotes the different axes a or c. Open circles indicate the approximate temperature of the broad shoulders of C4f/T below TN, gray squares the position of the maxima of the Schottky anomalies, and red open diamonds the temperature of the C4f maximum. The inset shows an enlarged view of the AF2 and AF3 phases. (b) Entropy S(B) at different fixed temperatures. (c) Frustration parameter fS = TS/TN vs. B. For B >Bc3, C4f/T at T = 0.5 K is plotted against B. All lines are guides to the eye. Figure reproduced with permission from Lucas et al., Ref. [64]. Copyright 2017 by the American Physical Society. |
The hybridization strength can be tuned by field and it is possible to liberate the frustrated moments from Kondo screening prior to the suppression of AFM, yielding a metallic spin liquid state in a certain field range. A comprehensive entropy analysis of CePdAl as a function of field[64] suggests that the frustration level is enhanced when crossing the phase boundary at Bc1 ∼ 3.25 T and reaches its highest value at Bc2 ∼ 3.4 T from AF2 to AF3 phase, confirming the boosted frustration and entropy as shown in Fig.
Characterizing the order parameter symmetry of the superconducting state is important for understanding the nature of the superconductivity and the microscopic mechanism leading to its formation and an important aspect of this is measuring the structure of the superconducting gap. In the case of the CeTIn5 materials, the presence of line nodes, that is lines across the Fermi surface where the superconducting gap goes to zero, could be inferred in CeCoIn5 and CeIrIn5 from zero-field measurements of the specific heat,[66] thermal conductivity,[66] and magnetic penetration depth.[67,68] However measurements in field allow for not only the presence of nodes to be ascertained but for their positions in
In Fig.
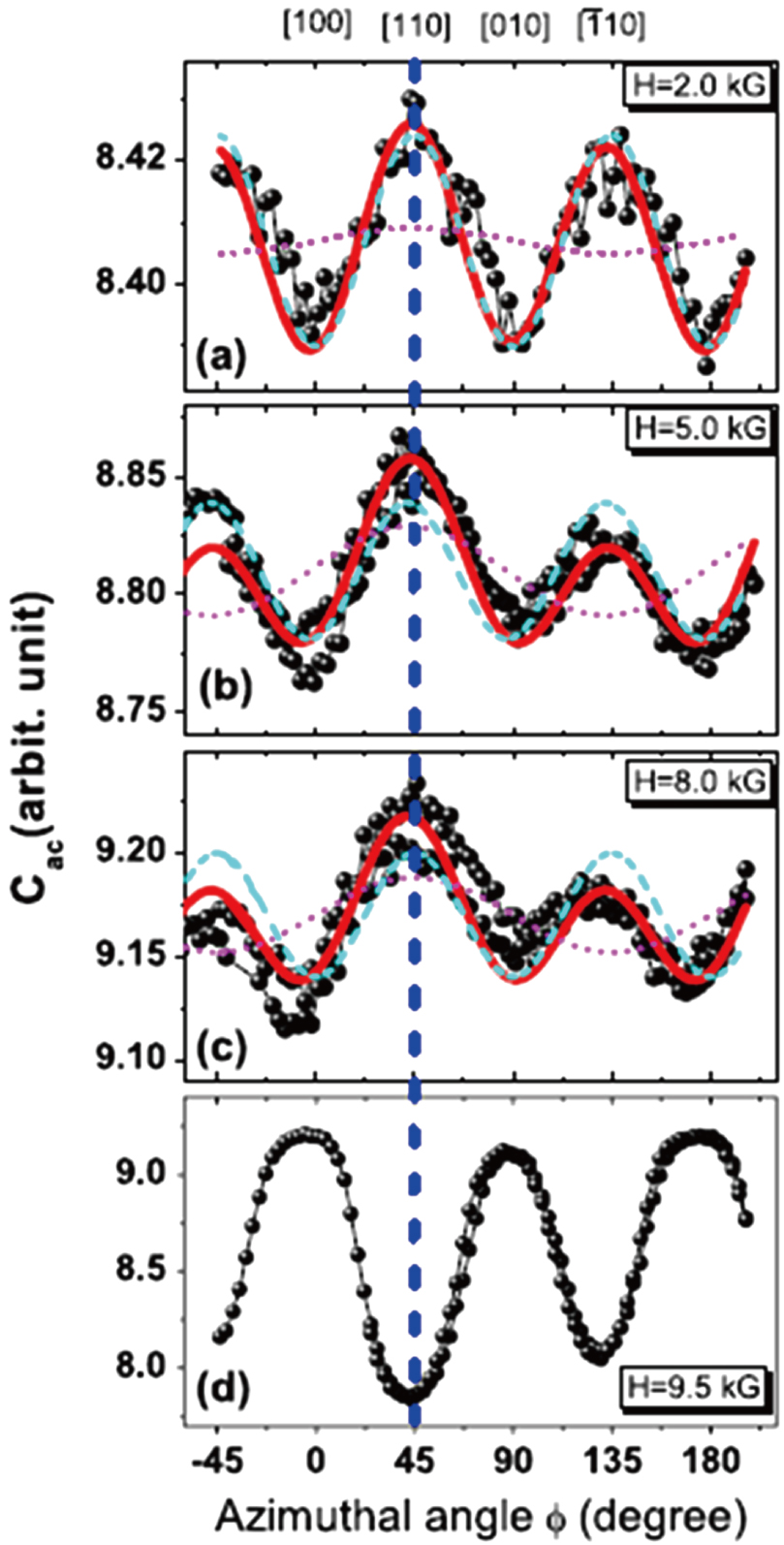 | Fig. 10. Field-angle dependence of the heat capacity of CeIrIn5 at 2.05 GPa, when a field is applied at an angle ϕ to the [100] direction. Figure reproduced with permission from Lu et al., Ref. [69]. Copyright 2002 by the American Physical Society. |
Applied magnetic fields can also lead to additional novel behaviors in superconductors. The application of magnetic fields generally leads to the breaking of Cooper pairs by two mechanisms, the orbital effect and paramagnetic limiting. The orbital pair breaking effect arises from the kinetic energy of supercurrents surrounding the vortex flux lines making the superconducting state energetically unfavorable. Meanwhile the paramagnetic limiting effect arises from the Zeeman splitting of the electron bands. When this Zeeman energy becomes sufficiently large compared to the superconducting condensation energy, superconductivity will often be destroyed. Although in most superconducting systems the orbital limiting effect primarily determines the magnitude of the upper critical field, when the paramagnetic limiting mechanism dominates, novel phases have been predicted such as the Fulde–Ferrell–Larkin–Ovchinnikov (FFLO) state.[74,75] This state has a spatially modulated order parameter including a periodic arrangement of normal and superconducting regions, and the Cooper pairs have a finite center-of-mass momentum.
CeCoIn5 had been considered to be a good candidate for the realization of the FFLO state, which has the required dominance of paramagnetic limiting and is in the clean limit.[66,76] Furthermore it was found that at fields larger than 4.7 T applied along the c-axis (temperatures below 0.31Tc), the transition from the normal to superconducting state changes from second-order to first-order, which is expected for Pauli limited superconductors.[76] In addition, at higher fields in the region where the superconducting to normal transition is first-order, an additional transition was found in specific heat measurements at lower temperatures in the superconducting state,[77,78] which was taken as evidence for the FFLO state. In particular, it was found that this transition at TFFLO disappeared when Tc < TFFLO, demonstrating an intrinsic link between this transition and the superconducting phase. Meanwhile, while NMR studies all found distinct changes in this high field Q’-phase, conflicting results were also reported.[79–81] In one study, the appearance of a new higher field resonance line was reported within the Q-phase, where the value of the Knight shift rapidly approached the normal state value with decreasing temperature.[79] This was taken as evidence for the coexistence of normal and superconducting regions in this high field regime, and therefore indicated that this did indeed correspond to the FFLO phase. On the other hand, different results were reported in another NMR study, where it was found that the spin-susceptibility in the Q-phase was enhanced compared to that in the homogenous superconducting state, yet still less than the normal state value.[80] This is inconsistent with the simple picture of alternating normal and superconducting regions in the FFLO state. It was also subsequently reported that the broadening of the NMR spectra was different for each of the crystallographic sites.[81] Such a variation cannot be simply explained by the inhomogeneity arising from the modulation of the order parameter in the FFLO state, since the length scales of these variations are considerably larger than the unit cell, and therefore it would be expected that there should be no difference for the different sites. Instead, these results give evidence for the occurrence of long range magnetic order of localized Ce moments. These unusual results point to a very different relationship between superconducting and magnetism in CeCoIn5, where instead of an antagonistic relationship between these phases, the occurrence of superconductivity is required for the appearance of long range magnetic order.
Direct evidence for this magnetic order was later reported in single crystal neutron diffraction measurements for fields applied along the [1-10] direction, where magnetic Bragg peaks corresponding to an ordering wavevector of (q, q, 0.5) were reported, with q ∼ 0.44 (Fig.
 | Fig. 11. Neutron diffraction intensity at a position (h, h, 0.5) as a function of h for CeCoIn5 measured in various high fields close to Hc2. The black circles display the data in the superconducting state, while the grey circles are in the normal state. It can be seen that in the superconducting state the magnetic Bragg peak appears corresponding to the Q-phase, which is absent when the system becomes normal. Figure reproduced with permission from Kenzelmann et al., Ref. [82]. Copyright 2008 AAAS. |
In general, for a magnetic ordering wave vector (q, q, 0.5), there are two possible SDW domains, one with
 | Fig. 12. (a) The intensity of the neutron diffraction peaks of the two SDW vectors |
In intermetallic systems, the observation of quantum oscillations in high magnetic fields provides important information about the Fermi surface, while in insulators, the lack of electronic bands crossing the Fermi level should preclude the occurrence of quantum oscillations. However, this seemingly obvious truth was called into question following the discovery of quantum oscillations in the Kondo insulator SmB6 via high field measurements of the dHvA effect.[15–17]
Two aspects in particular appear to separate SmB6 from regular band insulators. Firstly, SmB6 has generally been considered to be a Kondo insulator where the insulating gap opens at low temperatures due to the strong electronic correlations. As a result of the strong hybridization between the lattice of 4f electrons and the conduction electrons, renormalized heavy bands with very large effective masses form at low temperatures, separated by a hybridization gap. In Kondo insulators, the Fermi level lies within this gap, yielding a low temperature insulating state.[88] In SmB6, this is manifested by an extremely large increase in the resistivity at low temperatures, which increases as the temperature is decreased.[89,90] More recently, it was proposed that some Kondo insulators can also be characterized as topological insulators.[14] In this case, the resulting insulating electronic structure emerging due to the strong hybridization has a non-trivial Z2 index. Here the bulk band structure corresponds to a different topological index to the vacuum, which has a trivial topology. As a result, at the boundary between the bulk and vacuum, i.e., the surface of the sample, the insulating gap must vanish, and therefore conducting metallic surface states are anticipated. One of the longstanding mysteries of SmB6 is that below around 4 K, rather than continuing to decrease with decreasing temperature, the resistivity plateaus and changes little as the material is further cooled. Recent careful transport measurements have suggested that these “in-gap” states in fact correspond to surface conduction, providing experimental evidence for conducting surface states and therefore for SmB6 being a topological Kondo insulator.[18–20,91–93]
Besides the anomalous low temperature conduction, another unusual observation for an insulator found in SmB6 is that of quantum oscillations via measurements of the dHvA effect. This phenomenon has been reported by two different research groups using torque magnetometry, on samples grown by two different methods, as displayed in Fig.
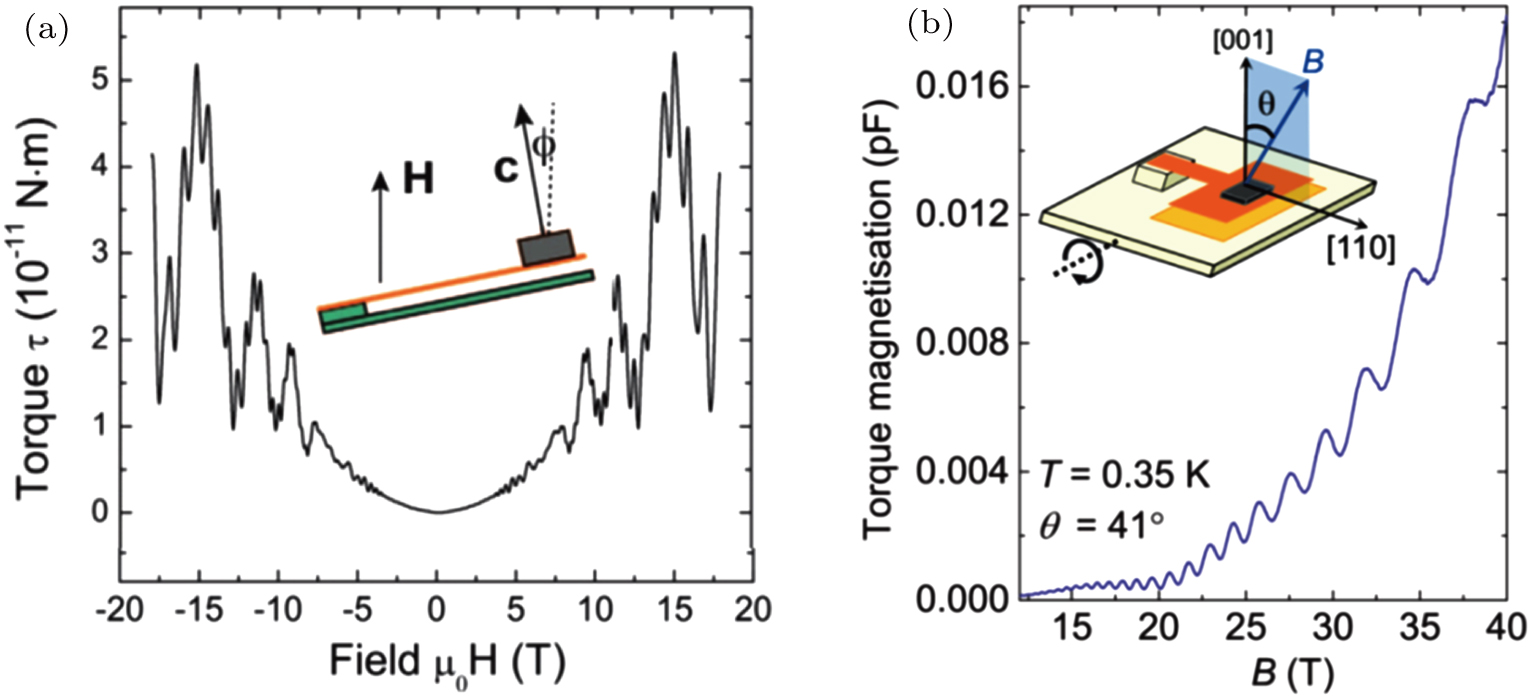 | Fig. 13. Quantum oscillations in the topological Kondo insulator SmB6 from measurements of the field dependence of the torque magnetometry. The measurements were performed by two different groups, with panel (a) reprinted with permission from Li et al., Ref. [15]; copyright 2014 AAAS, and panel (b) reprinted with permission from Tan et al., Ref. [16]; copyright 2015 AAAS. |
 | Fig. 14. Angular dependence of the quantum oscillation frequencies of SmB6 from Ref. [15] (a) and Ref. [16] (b). In the case of the former, the angular dependence was reported as being consistent with a 2D Fermi surface, as expected if the quantum oscillations arise from a surface state. On the other hand, the angular dependence of the frequencies in panel (b) was reported to be much more consistent with three-dimensional Fermi surfaces, pointing to a bulk origin. Panel (a) is reprinted with permission from Li et al., Ref. [15]; copyright 2014 AAAS, and panel (b) is reprinted with permission from Tan et al., Ref. [16]; copyright 2015 AAAS. |
On the other hand, Tan et al.[16] also observed quantum oscillations, which were reported over a wider frequency range, up to values larger than 10kBT. It was suggested by the authors that such large frequencies cannot be accounted for by surface states, due to the need for a correspondingly large mean-free path longer than the depth of the surface layers. Moreover, the angular dependences of the frequencies, which are also displayed in Fig.
Topological Kondo insulators are examples of gapped topological materials, where there is a gap in the topologically non-trivial bulk electronic structure, and the Fermi level lies within the gap. Recently, gapless topological semimetals with strong electronic correlations have also been increasingly studied. Examples of gapless topological materials include Dirac and Weyl semimetals, which have bulk band structures hosting linear band crossings, where the nearby excitations are well described by either Dirac or Weyl fermions, respectively.[22,23,97–100] It is of particular interest then to explore examples of such topological materials with strong electronic correlations, to examine the interplay of these two effects.
The R(Sb,Bi) (R = rare earth) family of materials are examples where these effects have been studied, in particular due to the potential for tuning the correlations and electronic structure by substituting with different rare earth elements. Studies of this series of materials were spurred by the finding that LaSb shows a plateau in the resistivity at low temperatures, which was suggested to be similar to that seen in SmB6,[101] although angle resolved photoemission spectroscopy (ARPES) studies cannot agree whether there is a non-trivial topology.[102,103]
High field measurements have been important for probing the non-trivial topology in these materials in two principal ways. Firstly, studies of quantum oscillations either using the dHvA or SdH effects can be utilized to probe the non-trivial Fermi surface, in particular they can be used to look for a non-trivial Berry phase. This can be performed by analyzing the Landau indices, whereby the oscillations are examined as a function of 1/B, the positions of either the oscillation maxima or minima are indexed, and the data are fitted linearly to determine the residual value. Here the value of the residual Landau index provides information about whether or not there is a non-trivial Berry phase, as well as the dimensionality of the Fermi surface.[24,25] For these measurements, high magnetic fields are particularly important, so as to probe the low lying Landau indices, allowing for an accurate determination of the intercept. The analysis of SdH oscillations in SmSb revealed a residual Landau index corresponding to a non-trivial Berry phase, which could be determined with a low degree of uncertainty due to magnetoresistance measurements being performed in pulsed fields up to 60 T.[27] Moreover, at low temperatures there was a significant deviation in the temperature dependence of the SdH oscillation amplitudes which could not be accounted for by the Lifshitz–Kosevich expression. A deviation from Lifshitz–Kosevich theory has also been observed in some dHvA measurements of SmB6,[16] but in the case of SmSb, anomalous behavior is only seen in SdH oscillations, whereas dHvA measurements show standard behavior. On the other hand, other RSb compounds such as PrSb show evidence for a trivial Berry phase from the Landau index analysis,[104] suggesting that substituting for different rare earth elements can tune the band topology.[105,106]
Another important probe for looking for Weyl fermions is from the presence of the chiral anomaly, which can be inferred from a negative longitudinal magnetoresistance. Weyl semimetals host Weyl points with different chiralities, and the chiral anomaly arises due to the parallel magnetic and electric fields pumping charges from one Weyl point to another of opposite chirality, which in turn leads to a population imbalance.[28,29] Evidence for Weyl fermions was found in the magnetic Kondo system CeSb from the observation of signatures of the chiral anomaly from the measurements of the longitudinal magnetoresistance. CeSb orders antiferromagnetically at low temperatures, but as shown in Fig.
 | Fig. 15. (a) Resistivity of CeSb as a function of field, when the applied field is parallel to the current direction. At low temperatures, a negative longitudinal magnetoresistance is observed after the transition from the antiferro-ferromagnetic (AFF) state to the field-induced ferromagnetic (FM) state. (b) Schematic diagram of how Weyl nodes occur in the field induced FM state of CeSb. The spin–orbit coupling gaps out the degenerate band crossing points, giving rise to a band inversion. The breaking of time reversal symmetry in the field-induced FM state splits the degenerate bands, giving rise to doubly degenerate band crossing points, which correspond to Weyl nodes. Both panels are reproduced from Guo et al., Ref. [31]. |
Meanwhile evidence for Weyl fermions from magnetotransport measurements was also observed in the heavy fermion semimetal YbPtBi,[32] where the extremely large Sommerfeld coefficient of around 8 J⋅mol−1⋅K−2 indicates that the electronic bands are strongly renormalized at low temperatures due to the Kondo interaction.[107] At elevated temperatures above 20 K, the magnetotransport shows clear signatures of the chiral anomaly, exhibiting the expected temperature, field, field-angle, and doping dependences.[32] Furthermore, the presence of Weyl fermions is supported by the electronic structure calculations and ARPES measurements, showing evidence for triply degenerate fermion points in zero field, which are each split into a Weyl point and a trivial crossing in applied fields. At low temperatures, the evidence for the chiral anomaly disappears, yet as displayed in Fig.
 | Fig. 16. Evidence for Weyl fermions at low temperatures in the heavy fermion state of YbPtBi. (a) Anomalous contribution to the Hall resistivity, after subtracting the normal contribution from the charge carriers. (b) Topological Hall angle at different temperatures after subtracting a contribution from the Hall resistivity proportional to the magnetization. The significant value at low temperatures arises from the Berry curvature generated by the Weyl nodes. (c) Temperature dependence of the specific heat as Cp/T in various applied fields. The solid line shows a fit to a Kondo model, which cannot describe the low temperature data. (d) Cp/T vs. T2 in various applied fields. The linear relationship reveals a cubic temperature dependence of the specific heat, which is a signature of the linear dispersion of heavy fermion bands expected in the vicinity of Weyl points. Figure reproduced from Guo et al., Ref. [32]. |
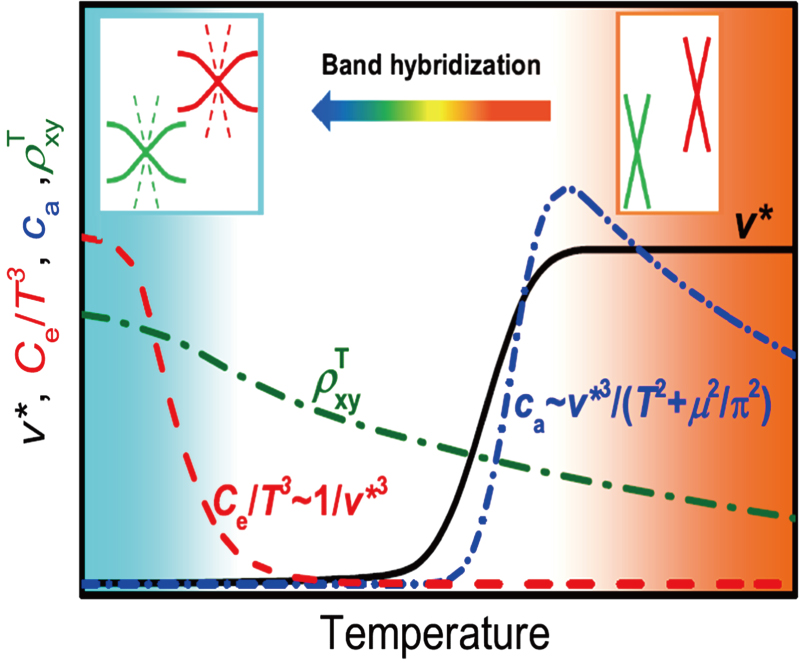 | Fig. 17. Schematic diagram to illustrate the evolution of Weyl fermions in YbPtBi, as the temperature is reduced and the Kondo interaction becomes stronger. The dramatic decrease of the Fermi velocity v* at low temperatures leads to the disappearance of the chiral anomaly contribution ca, but the large entropy associated with the renormalized bands leads to a sizeable cubic term in the temperature dependence of the specific heat Ce. Meanwhile a sizeable topological Hall effect contribution  |
To summarize, measurements under high magnetic fields are important for understanding the variety of fascinating behaviors of heavy fermion systems. Measurements at high magnetic fields and low temperatures are important for experimentally probing the band structure, which provides a vital basis for understanding the physical properties. Tuning heavy fermion systems with field can show a marked difference to other tuning parameters, which can lead to different types of quantum critical behaviors. Nevertheless there are still many puzzling aspects associated with field induced quantum criticality and the interplay between magnetic order and the Kondo interaction when a field is applied. It is particularly important to understand systems exhibiting multiple types of QCP when tuned with different parameters, and the extent to which these QCPs can be universally classified will be the subject of future studies. Furthermore, for many recent topics of interest in heavy fermion systems such as the role of topology or geometric frustration, measurements in magnetic fields have proved important for unveiling many of the novel properties.
High magnetic fields are also vital for directly probing the Fermi surface, which is a key method for classifying the different types of quantum critical points. Additional work is also required in this area to determine whether quantum phase transitions can be universally classified, and what happens to the quasiparticles upon approaching the different types of quantum critical points. A major experimental challenge in this regard is the need to measure the physical properties with a wide range of experimental tools both at very low temperatures and high magnetic fields, and the rapid development of measurements in high fields has provided a wealth of new information in recent years. Meanwhile Fermi surface probes in high magnetic fields are also important for probing topological materials. While topological materials have been well studied in weakly correlated systems, there are fewer examples of correlated topological materials. In particular, topological heavy fermion systems where the electronic bands are strongly renormalized by the Kondo interaction can allow for the interplay between topology and correlations to be examined.
Although high fields have been important for determining the superconducting order parameter, the novel superconducting states of heavy fermion superconductors can also show a number of unusual field-induced behaviors which still need to be explored. In particular, the so-called Q-phase of CeCoIn5 shows an especially unusual and intriguing interplay of superconductivity and magnetism. In addition, the superconducting states of other heavy fermion superconductors are often not well characterized, which often require measurements both under pressure and very low temperatures to understand the superconducting properties.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] | |
| [90] | |
| [91] | |
| [92] | |
| [93] | |
| [94] | |
| [95] | |
| [96] | |
| [97] | |
| [98] | |
| [99] | |
| [100] | |
| [101] | |
| [102] | |
| [103] | |
| [104] | |
| [105] | |
| [106] | |
| [107] |

