Project supported by the National Natural Science Foundation of China (Grant Nos. 11774088 and 11474090), the Hunan-Provincial Natural Science Foundation of China (Grant No. 13JJ3076), and the Science Research Program of Education Department of Hunan Province of China (Grant No. 14A127).
Project supported by the National Natural Science Foundation of China (Grant Nos. 11774088 and 11474090), the Hunan-Provincial Natural Science Foundation of China (Grant No. 13JJ3076), and the Science Research Program of Education Department of Hunan Province of China (Grant No. 14A127).
† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11774088 and 11474090), the Hunan-Provincial Natural Science Foundation of China (Grant No. 13JJ3076), and the Science Research Program of Education Department of Hunan Province of China (Grant No. 14A127).
The goal of this article is to establish the conditions of excitation where one has to deal with ultrasound contrast agent (UCA) microbubbles pulsating near biological tissues with spherical boundary in ultrasound field for targeted drug delivery and cavitation-enhanced thrombolysis, etc., and contributes to understanding of mechanisms at play in such an interaction. A modified model is presented for describing microbubble dynamics near a spherical boundary (including convex boundary and concave boundary) with an arbitrary-sized aperture angle. The novelty of the model is such that an oscillating microbubble is influenced by an additional pressure produced by the sound reflection from the boundary wall. It is found that the amplitude of microbubble oscillation is positively correlated to the curve radius of the wall and negatively correlated to the aperture angle of the wall and the sound reflection coefficient. Moreover, the natural frequency of the microbubble oscillation for such a compliable wall increases with the wall compliance, but decreases with the reduction of the wall size, indicating distinct increase of the natural frequency compared to a common rigid wall. The proposed model may allow obtaining accurate information on the radiation force and signals that may be used to advantage in related as drug delivery and contrast agent imaging.
Research of acoustical response of ultrasound contrast agent (UCA) microbubbles has attracted wide interests from both the medical and acoustical communities, not only for providing a better understanding of their complex dynamics, but also for their potential use for targeted drug delivery and molecular imaging.[1–3] Apart from these medical applications, UCA microbubble sonication is being recently utilized in several other medical areas, such as thrombus dissolution, gas embolotherapy, sonoporation, and micro-pumping.[4–6] In each case, it requires consistent mathematical and physical knowledge of sonicated microbubble oscillation near different types of boundaries.
Some experimental studies[7–9] have investigated microbubble dynamics in confined spaces and have shown that the proximity of a boundary can produce considerable changes in the oscillation amplitude of a microbubble and its scattered echo.[10,11] Moreover, there are some results indicating that microbubble collapse is mitigated as the driving frequency increases, or the microbubble is closer to the rigid boundary.[12] Theoretical attempts to model microbubble sonication in a confined configuration usually utilizes the boundary integral method,[11] finite element method[13] or method of images,[14,15] which describes the nonlinear oscillations of a microbubble near rigid boundaries and on the effects of boundaries such as a single wall, two parallel walls, or a tube, and so on. Most investigations focused on a cavitation microbubble occurring near a flat boundary. In fact, microbubble cavitation in a curved boundary is not uncommon in human body tissues. It is well known that red blood cells, which contain large amount of concave shape and are approximately 7.5–8.7 μm in diameter[16] whereas the mean diameter of UCA microbubbles is generally less than 5 μm.[17] Medical imaging shows the growing atherosclerotic plaque is ellipsoid or spherical in shape,[18] and there are a lot of irregular filling cavities in the clot aggregated by platelets and red blood cells crowded.[19,20] Cavitation microbubbles often create many cavities or pits on the surface of the target object during the removal of kidney and bladder stones with focusing of the shockwave.[21] In addition, microbubble forms a jet directed toward the interface due to interaction of cavitation microbubbles with cell membranes and produces a porous wall during sonoporation,[22] which potentially has a significant impact on membrane permeation observed in the experiment.[23] Accordingly, it is imperative to understand the bubble dynamics in soft tissues with curved boundaries or cavities for such as targeted drug delivery,[24] and so on.
A number of studies have been dedicated to the microbubble dynamics near a curved boundary. For example, Tomita et al.[25,26] generated a laser-induced microbubble near a curved rigid boundary and the experiments present that the velocity of the micro jet increases while the shape of the rigid boundary changes from concave into convex. Wu et al.[27] reported an experimental study of microbubble dynamics near a convex free surface and focus on the strength of the micro jet when microbubble collapses. Obreschkow et al.[28] studies the behavior of a bubble in a droplet in micro gravity. They observed two liquid jets escaping from the drop when the microbubble collapses, and a shorter microbubble life time in the droplet than the microbubble in an infinite fluid. Also, the spike and the splash on the concave free surface are not as violent as a flat free surface.
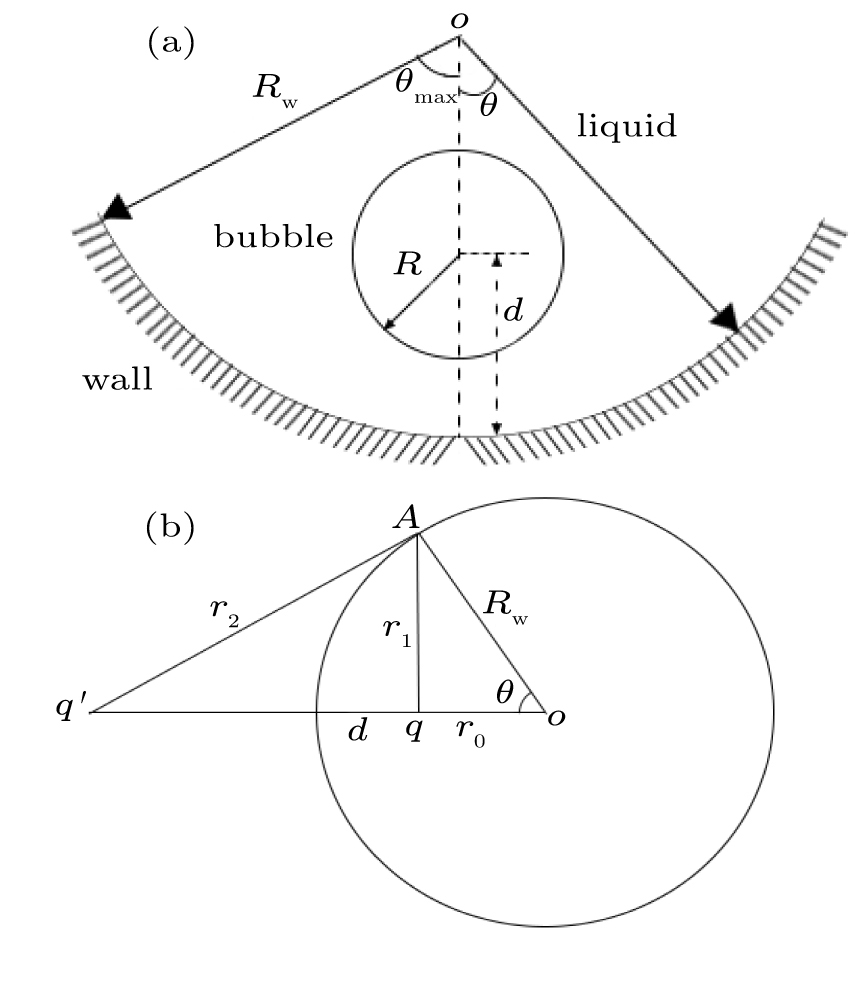
However, the microbubble dynamics near a spherical boundary with arbitrary-sized aperture angle has received less attention, and the influence of the geometric parameters of the boundary remains poorly understood to date. In this paper, we assume that an oscillating microbubble is influenced by additional pressure come from sound reflections on a wall.[29] The sound reflection combining with the image method are employed to demonstrate the microbubble confinement near the wall. Considering that UCA-type microbubbles have immediate biomedical applications such as the delivery of drugs and the instigation of sonoporation, the geometric setups and parameters are chosen to be of relevance for intravascular microbubble dynamics in medicine. This article focuses on the influences of the concave wall sizes and the wall properties, and specially studies the natural frequency responses of wall properties, and finally summarizes our results.
Suppose a spatially uniform ultrasound pressure field: the ultrasound wave length is of the order of 1 mm and thus much larger than the dimension of the region of interest surrounding a UCA microbubble.[30] The microbubble retains a spherical shape throughout the simulation for low expansion ratio.[31]
We further assume that the fluid surrounding the microbubble is incompressible, and the liquid flow is irrotational. The velocity potential φ, fluid velocity v and acoustic pressure p obey the equation of continuity and are written in terms of a scalar velocity potential as[32]
To describe the confinement effect on the microbubble oscillation, the concave wall is replaced by an identical image bubble oscillating in-phase with a real microbubble and positioned at the mirrored image point. The dynamics of the real microbubble is influenced by the pressure emitted by the image microbubble or by the wall. To this end, suppose that a point source q located at distance r from the center, inside the sphere, has an image q′ at distance r′ from the center. The point source q, its image, and the center of the sphere lie on a straight line, as is the script on the left-hand side of Fig.
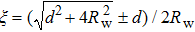
We assume that the boundary wall behaves as a point source with q′ and both point-source microbubbles are equal, pulsating in phase. We substitute Eq. (
The dynamics of a UCA microbubble in a spherical boundary may be described using a modified Rayleigh–Plesset equation[34] that accounts for the reflected pressure.
Assuming that the pulsation amplitude is small, namely, R(t) = R0 (1 + x(t)), where |x(t)| ≪ 1, we can obtain the natural frequency of a UCA microbubble near a sphere wall,
We first validate our model by comparing to the estimates of other investigators. When taking no account of translational microbubble motion, a comparison of the influence of the curved surface of two models, i.e., Eq. (
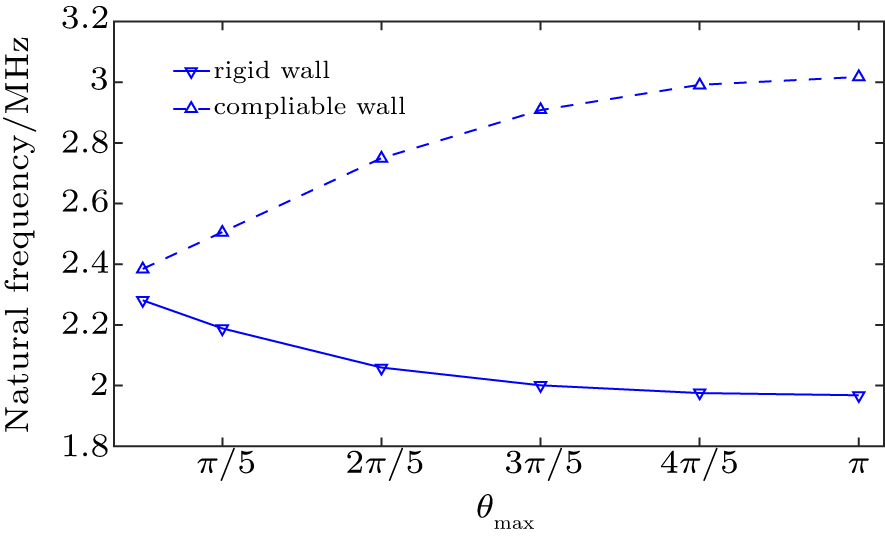
We next consider the correlation between constraint coefficient and aperture angle. We simulated Eq. (
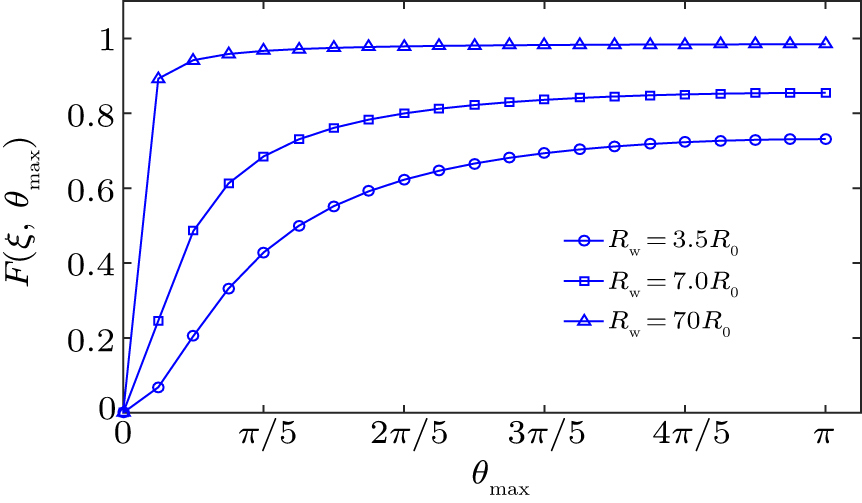 | Fig. 3. Comparison of the constraint coefficient at different θmax for a microbubble at the distance of d = 1.1R0 near the convex spherical surface. |
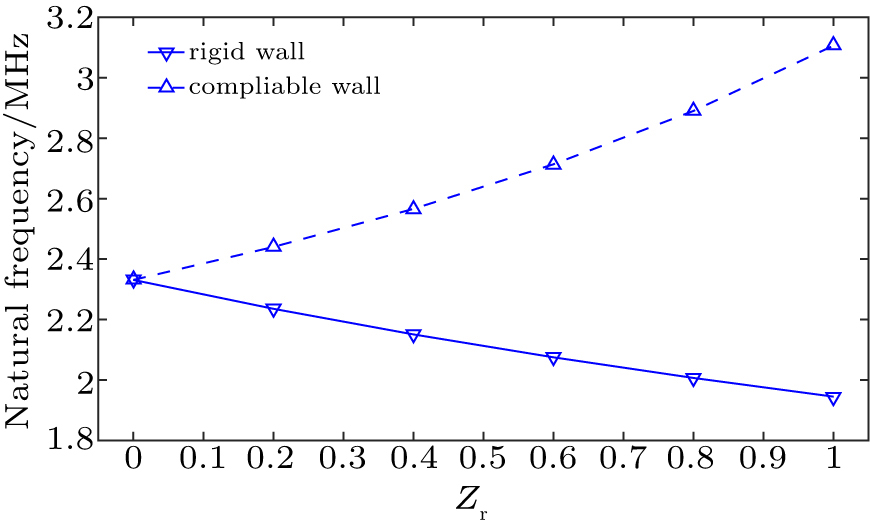
We further explored in detail the natural frequency of oscillation of a UCA microbubble confined in a concave sphere wall. Wall rigidity, microbubble size and microbubble position are taken into account for evaluating the effects on the natural frequency of a UCA microbubble oscillation. Figure
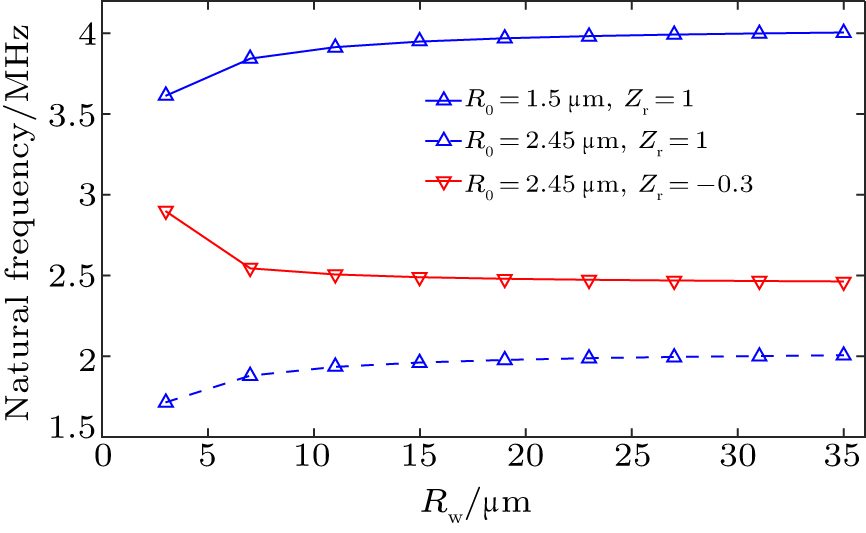 | Fig. 4. The microbubble natural frequency as a function of microbubble radius for the microbubble lying near concave wall at the distance of d = 1.1R0 and θmax = π. |
Figure
In the above simulation results the microbubble natural frequency is susceptible to the type of concave wall. Equations (
We have presented a model to study a UCA microbubble response confined in a spherical boundary. The present model can be used not only for the dynamic behavior of a microbubble confined in concave sphere boundary but also for demonstrating the microbubble constraint near convex sphere boundary. The influence of an additional pressure on microbubble can be demonstrated by the reflected pressure from wall surface. Two kinds of boundaries for a concave wall have been considered, i.e. a rigid wall and a compliable wall, which may correspond to the vasculature of a developing tumor. Numerical results demonstrate that the natural frequency of mircobubble in a rigid wall is smaller compared to that in unbounded field, and further decreases with the reducing concave size. Interestingly, this frequency increases with the decreasing concave wall size. Moreover, the natural frequency of microbubble in the unbounded field is the lower limit of the bubble natural frequency in a compliable wall and the upper limit in an absolute rigid wall. For medical applications, the changes of the frequency spectrum of the microbubble show the changes of the material property including concave wall size and its compliance.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] |