† Corresponding author. E-mail:
Project supported by the Science and Technology Program of Guangdong Province, China (Grant No. 2015B010112002) and the Science and Technology Project of Guangzhou City, China (Grant No. 201607010250).
The electronic structures and optical properties of β-Ga2O3 and Si- and Sn-doped β-Ga2O3 are studied using the GGA + U method based on density functional theory. The calculated bandgap and Ga 3d-state peak of β-Ga2O3 are in good agreement with experimental results. Si- and Sn-doped β-Ga2O3 tend to form under O-poor conditions, and the formation energy of Si-doped β-Ga2O3 is larger than that of Sn-doped β-Ga2O3 because of the large bond length variation between Ga–O and Si–O. Si- and Sn-doped β-Ga2O3 have wider optical gaps than β-Ga2O3, due to the Burstein–Moss effect and the bandgap renormalization effect. Si-doped β-Ga2O3 shows better electron conductivity and a higher optical absorption edge than Sn-doped β-Ga2O3, so Si is more suitable as a dopant of n-type β-Ga2O3, which can be applied in deep-UV photoelectric devices.
β-Ga2O3 is an emerging semiconductor material with a wide bandgap of about 4.9 eV. β-Ga2O3 exhibits fascinating physical properties and chemical stability, such as good transparency and a critical breakdown field of up to 8 MV/cm, which has made it a focus of attention in recent years.[1,2] With these advantages, β-Ga2O3 is considered to be a promising transparent conducting material operating from the visible to the deep-ultraviolet spectrum for photodetector and other optoelectronic devices.[3,4]
However, the poor electrical conductivity of β-Ga2O3 hinders its application as a transparent conducting oxide (TCO).[5] It is well known that doping is an effective way to improve the photoelectric properties of materials, including conductivity, mobility and absorptivity. Si is regarded as a suitable dopant for n-type β-Ga2O3 because excess free electrons will be generated after doping. Further, the oxides of Si and Ga have a similar melting point, which is beneficial for adjusting the growth temperature and obtaining a high doping concentration. Zhang et al.[6] obtained a Si-doped β-Ga2O3 film using the pulsed laser deposition (PLD) technique, and the highest doping concentration is 9.1 × 1019 cm−3, but the corresponding conductivity is only 2.0 S · cm−1. The low conductivity is due to the amorphous-like structure of the Si-doped β-Ga2O3 and blockage of electronic transmission paths. Takakura et al.[7] deposited Si-doped β-Ga2O3 film by radio-frequency (RF) magnetron sputtering, and found that the optical gap of the Si-doped β-Ga2O3 is wider than that of β-Ga2O3. Recently, a homoepitaxial Si-doped Ga2O3 film produced by PLD, with a high carrier concentration of 1.74 × 1020 cm−3 and ultrahigh conductivity of 732 S/cm, was reported,[8] but its conductivity is still far below that of commercial ITO film or Al-doped ZnO film. Sn is another promising dopant as a donor for improving the conductivity of β-Ga2O3 because excess free electrons will be generated when Sn4+ substitutes Ga3+. Orita et al.[1] deposited n-type Ga2O3 film by Sn doping and obtained the best conductivity of 8.2 S · cm−1. Ohira et al.[5] prepared Sn-doped β-Ga2O3 by the float-zone method, found that Sn was dispersed in β-Ga2O3 uniformly, and suggested that Sn be substituted in the Ga site in the β-Ga2O3 lattice, but they did not discuss the optical properties of Sn-doped β-Ga2O3. Baldini et al.[9] grew Si- and Sn-doped homoepitaxial β-Ga2O3 films by metal organic vapor phase epitaxy (MOVPE), and the highest electron concentrations of 8 × 1019 cm−3 for Si-doped β-Ga2O3 and 1 × 1019 cm−3 for Sn-doped β-Ga2O3 were obtained. The corresponding electron mobilities were 54.37 cm2/V · s and 32 cm2/V · s, but the conductivities and optical properties were not analyzed.
First-principles calculations based on density functional theory (DFT) have been extensively used for scientific research, and some material properties have been successfully parsed, such as electronic structures, optics and magnetism. Varley et al.[10] found that a stable structure is obtained when Si4+ replaces Ga3+ in the four-fold coordination according to the calculated total energy of Si-doped Ga2O3 by using first principles. Siah et al.[11] reported that Sn4+ prefers six-fold coordination and tends to substitute the Ga3+ octahedral site for Sn-doped β-Ga2O3. Zhang et al.[12] calculated the electronic structures and optical properties of β-Ga2O3 and Sn-doped β-Ga2O3 by using the generalized gradient approximation (GGA) exchange–correlation function based on DFT, but the calculated bandgap of β-Ga2O3 is only 2.315 eV, which is less than half of the experimental value (4.9 eV[1]). The underestimation of the bandgap is a well-known drawback of the standard DFT calculation due to the lack of precise consideration of the exchange–correlation potential, but it can be corrected by the scissors approximation,[13] hybrid-functional,[14] and GGA + U methods.[15] In order to obtain calculated bandgaps that are close to the experimental data, Li et al.[14] calculated the electrical and optical properties of β-Ga2O3 and Si-doped β-Ga2O3 using the screened hybrid functional HSE06, but the calculated result shows that β-Ga2O3 is a direct-bandgap material, which is not consistent with the experimental result.[16] Lately, Dong et al.[15] calculated the influences of oxygen vacancies on the structural and optical properties of β-Ga2O3 by GGA + U approximation with the Hubbard U parameters of 7.0 eV and 8.5 eV for Ga and O ions, respectively. The calculated bandgap of β-Ga2O3 is 4.92 eV, which is in agreement with the experimental value, but the calculated peak of the Ga 3d state is located at about −14.8 eV, which deviates from the experimental result of −17.12 eV,[17] and so the Hubbard U value requires reconsideration. So far, there have been no reports on the electronic structures and optical properties of Si-doped and Sn-doped β-Ga2O3 by using GGA/LDA + U methods. There are also very few comparative research reports on the physical properties of Si-doped β-Ga2O3 and Sn-doped β-Ga2O3. To further understand the differences in the electronic structures and optical properties of Si-doped β-Ga2O3 and Sn-doped β-Ga2O3, the energy band structures, density of states and optical properties are calculated in this paper using the GGA + U method based on DFT.
β-Ga2O3 has a monoclinic structure and its space group is C2/m,[18] β-Ga2O3 has double chains of edge-sharing GaO6 octahedra and a single chain of vertex-sharing GaO4 tetrahedra along the y axis, which is beneficial to the movement of free electrons.[19] A 1 × 2 × 2 supercell of β-Ga2O3 is used as the father model and is shown in Fig.
The electronic structures and optical properties of β-Ga2O3 and TM-doped β-Ga2O3 (TM = Si,Sn) are calculated using the first-principles plane-wave pseudo-potential method based on density functional theory[20] as implemented in the CASTEP package.[21] The exchange–correlation potential is employed through the GGA within the Perdew–Burke–Ernzerhof (PBE) function.[22] The atomic cores are described by the ultra-soft pseudo-potential, and the valence electron configurations are [Ga] 3d104s24p1, [O] 2s22p4, [Si] 3s23p2 and [Sn] 5s25p2. In order to obtain the accurate bandgap of β-Ga2O3, the GGA + U method is adopted and the parameters of Ud,Ga and Up,O are set to be 14.0 eV and 8.35 eV, respectively. The energy cutoff of the plane-wave basis is set to be 450 eV for the calculation of electronic structures and 600 eV for the calculation of optical properties. A 2 × 4 × 2 mesh of the Monkhorst–Pack k-points[23] is used for the Brillouin zone integration in reciprocal space.[24] Before calculation, the atomic coordinates and cell volume of the models need to be optimized, and the energy tolerance, tolerance of the force, maximum stress and maximum displacement are set to be 1 × 10−5 eV/atom, 0.03 eV/Å, 0.05 GPa, and 0.001 Å, respectively. The structural optimization is completed when the above four parameters meet or exceed the setting precisions.
The optimized structure parameters of β-Ga2O3 and TM-doped β-Ga2O3 (TM = Si,Sn) are listed in Table
| Table 1. The structural parameters and formation energies of β-Ga2O3 and TM-doped β-Ga2O3 (TM = Si,Sn) under the GGA + U method. . |
To evaluate the structure stability of TM-doped β-Ga2O3 (TM = Si,Sn), the doping formation energies of β-Si0.0625Ga1.9375O3 and β-Sn0.0625Ga1.9375O3 are calculated according to the formula[30]
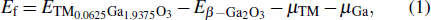 |
 |
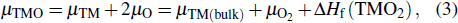 |
 |
 |
| Table 2. The average bond lengths of Ga–O, Si–O and Sn–O for TM-doped β-Ga2O3 (TM = Si,Sn). . |
To illustrate the effect of the Hubbard U on the band structure and density of states, the calculated band structures and densities of states (DOSs) of β-Ga2O3 under GGA and GGA + U methods are shown in Fig.
To further investigate the effect of the doping atom on the electronic structure of β-Ga2O3, the band structures and DOSs of β-Si0.0625Ga1.9375O3 and β-Sn0.0625Ga1.9375O3 obtained by the GGA + U method are shown in Fig. 
The total and the partial densities of states of β-Si0.0625Ga1.9375O3 and β-Sn0.0625Ga1.9375O3 are also given in Fig.
For a doped semiconductor with high doping concentration (i.e., >1019 cm−3), there are primarily two competing mechanisms affecting its optical gap: the Burstein–Moss effect[34] and the bandgap renormalization effect.[35] The Burstein–Moss effect causes bandgap widening due to the Fermi-band filling effect, marked as ΔEBM. The bandgap renormalization effect causes bandgap narrowing due to the many-body bandgap renormalization effect and the semiconductor–metal transition effect, labeled as ΔEBGN. The ΔEBM and ΔEBGN can be obtained by[36]
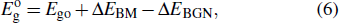 |
 |
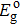
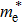
 |
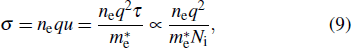 |
Optical properties are important for TCO materials and are expressed by the complex dielectric function ε(ω) = ε1(ω) + iε2(ω). The imaginary part ε2(ω) of the complex dielectric function is determined by the momentum matrix elements between the occupied and unoccupied wave functions. The real part ε1(ω) can be evaluated from imaginary part ε2(ω) using the Kramers–Kronig relationship, and the absorption coefficient α(ω) can be calculated according to the complex dielectric function. The above relationships are described by the following formulas:[38]
 |
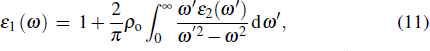 |
 |
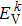
The imaginary parts ε2(ω) of the complex dielectric function of β-Ga2O3, β-Si0.0625Ga1.9375O3 and β-Sn0.0625Ga1.9375O3 in the x, y, and z directions are calculated and shown in Fig.
The absorption coefficients α(ω) of β-Ga2O3, β-Si0.0625Ga1.9375O3 and β-Sn0.0625Ga1.9375O3 in the x, y and z directions are plotted in Fig.
 | Fig. 5. The absorption coefficients of β-Ga2O3, β-Si0.0625Ga1.9375O3 and β-Sn0.0625Ga1.9375O3 in the (a) x-axis, (b) y-axis and (c) z-axis directions. The inset is a partial enlargement. |
To analyze clearly the difference in the peak edge, the spectra between 4.2 eV and 7 eV are also given in the insets of Fig.
In summary, the energy band structures, densities of states and optical properties of β-Ga2O3 and β-TM0.0625Ga1.9375O3 (TM = Si, Sn) are calculated and compared using the GGA + U method based on DFT. The calculated bandgap, Ga 3d-state peak and upper valence bandwidth of β-Ga2O3 are close to the experimental results if the Hubbard U parameters are set to 14 eV and 8.35 eV for the Ga d state and the O p state. Si- and Sn-doped β-Ga2O3 tend to form under O-poor conditions, and Si-doped β-Ga2O3 requires higher growth temperature compared with Sn-doped β-Ga2O3 because of the large bond length variation between Ga–O and Si–O, but Si-doped β-Ga2O3 has better electron mobility and conductivity than Sn-doped β-Ga2O3. Besides, the optical properties of Si- and Sn-doped β-Ga2O3 show significant anisotropy, and the average optical absorption edge of Si-doped β-Ga2O3 is larger than that of β-Ga2O3 or β-Sn0.0625Ga1.9375O3, so Si-doped β-Ga2O3 has advantages over Sn-doped β-Ga2O3 for applications in deep-ultraviolet photoelectric devices.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] |





