† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11474168 and 11747161), the Priority Academic Program Development of Jiangsu Higher Education Institutions, China, and the China Postdoctoral Science Foundation (Grant No. 2018M642293).
Single-photon entanglement (SPE) is an important source in quantum communication. In this paper, we put forward a single-photon-assisted noiseless linear amplification protocol to protect the SPE of an arbitrary polarization–time-bin qudit from the photon transmission loss caused by the practical channel noise. After the amplification, the fidelity of the SPE can be effectively increased. Meanwhile, the encoded polarization–time-bin features of the qudit can be well preserved. The protocol can be realized under the current experimental conditions. Moreover, the amplification protocol can be extended to resist complete photon loss and partial photon loss during the photon transmission. After the amplification, we can not only increase the fidelity of the target state, but also solve the decoherence problem simultaneously. Based on the above features, our amplification protocol may be useful in future quantum communication.
Entanglement is an important source in quantum communication. In the past few decades, entanglement has been widely used in quantum teleportation,[1–4] quantum secure direct communication,[5–12] quantum key distribution,[13–16] and so on.[17–24] Among the various entanglement forms, single-photon entanglement (SPE) with the form of 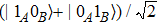
Unfortunately, during the distribution in a practical quantum channel, the single-photon qudit may be lost due to the channel noise. Photon transmission loss is a fundamental limitation in quantum communication, and will make the communication fidelity decrease exponentially with the channel length.[43] Noiseless linear amplification (NLA) is an effective method to overcome the photon transmission loss problem, and was first proposed by Ralph and Lund in 2009.[44] Since then, a large number of NLA protocols have been proposed successively.[45–64] In 2010, Gisin et al. proposed a theoretical heralded qubit amplifier for single-photon qubits. They first used this heralded qubit amplifier in device-independent quantum key distribution (DI-QKD) to lengthen the communication distance.[45] In 2012, Osorio et al. realized the heralded noiseless amplification of the single-photon qubit in linear optics in an experiment.[49] Later, Zhang et al. first used Gisin’s amplifier to protect the two-mode SPE.[50] In 2015, Zhou put forward the first nonlinear recyclable amplification protocol for SPE with the help of cross-Kerr nonlinearity.[56] In 2017, Monteiro et al. proposed a heralded amplification protocol of SPE and they adopted this amplification protocol in the DI-QKD. They showed that by exploiting the amplification protocol, they can maintain high-fidelity entangled states over loss-equivalent distances longer than 50 km.[57] Besides single-photon-assisted NLA protocols, in 2013, Scott et al. proposed an entanglement-assisted NLA protocol of a single-photon qubit.[58] Later, considering that ideal auxiliary single photons and auxiliary photon entanglement are difficult to obtain under current experimental conditions, the group of Sheng extended the entanglement-assisted amplification protocol to protect the SPE under imperfect auxiliary photon states generated by a current spontaneous parametric down-conversion source.[59–61] Although the amplification of SPE has been widely discussed, the previous NLA protocols cannot be used to protect the SPE of the polarization–time-bin qudit from photon loss. In this paper, we put forward an NLA protocol for protecting the SPE of the polarization–time-bin qudit assisted with some auxiliary polarized single photons. This NLA protocol only requires some common linear optical devices, which makes it realizable using current experimental technology. After the amplification, the polarization–time-bin encoding features of the single photon can be perfectly retained. Moreover, we will discuss the application of our NLA protocol to resist complete photon loss and partial photon loss. After performing the NLA protocol, we can not only increase the fidelity of the SPE, but also solve the decoherence problem in the spatial mode simultaneously.
The paper is organized as follows. In Section
In this section, we will explain the amplification protocol for the SPE of an arbitrary polarization–time-bin qudit. We assume that the photon source S generates an arbitrary polarization–time-bin qudit with the form
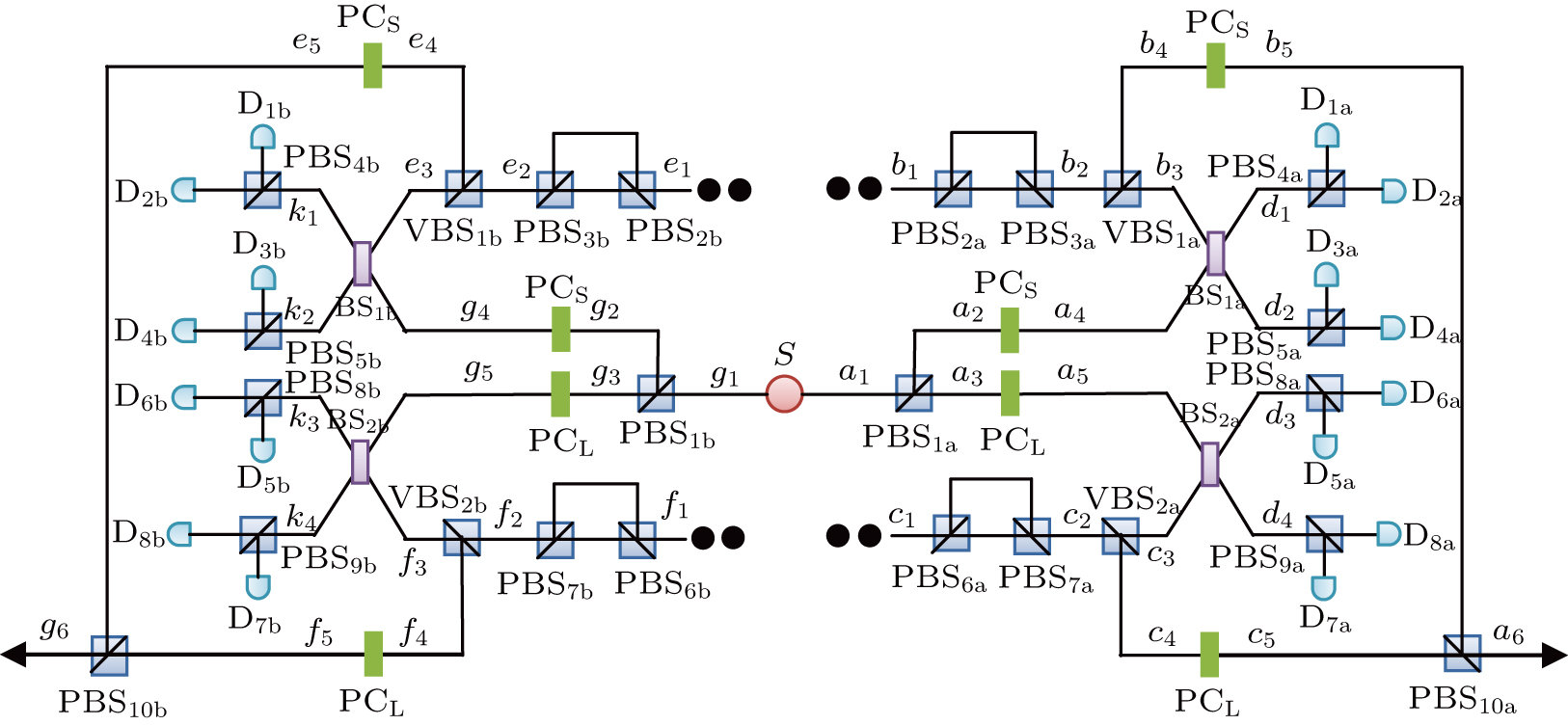
The schematic principle of this protocol is shown in Fig.
Then, Alice and Bob make the two auxiliary photons in each of the four spatial modes b1, c1, e1, and f1 enter a VBS with the transmittance of t. Here, we name the four VBSs as VBS1a, VBS2a, VBS1b, and VBS2b, respectively. After the VBSs, the auxiliary photon state will evolve to
On one hand, we first consider that the photonic qudit is not lost with the probability of F. In this case, the whole photon state is |Ψ1⟩ = |Φ⟩AB ⊗|φ2⟩. Alice and Bob make the single photon in a1 and g1 modes pass through PBS1a and PBS1b, respectively, which makes |Φ⟩AB in Eq. (
Afterwards, Alice and Bob let the photons in a4b3, a5c3, g4e3, and g5f3 modes enter four 50:50 BSs, respectively. We mark the four BSs as BS1a, BS2a, BS1b, and BS2b, respectively, which can make
Based on the Hong–Ou–Mandel bunching effect, Alice and Bob should make the photons in the two input modes arrive at the BS at the same time. In this way, the parties must accurately adjust the length of each line. After the BSs, |Φ2⟩AB in Eq. (
Next, Alice and Bob respectively detect the output photons in the d1d2d3d4 and k1k2k3k4 modes with the help of the PBSs and single-photon detectors Dia and Dib (i = 1,2,…,8). We can deduce that |HS⟩d1(d3), |HS⟩d2(d4), |HS⟩k1(k3), and |HS⟩k2(k4) will be respectively detected by D2a(6a), D4a(8a), D2b(6b), and D4b(8b), while |VL⟩d1(d3), |VL⟩d2(d4), |VL⟩k1(k3), and |VL⟩k2(k4) will be respectively detected by D1a(5a), D3a(7a), D1b(5b), and D3b(7b). It is worth noting that all the photon detectors Dia and Dib (i = 1,2,…,8) are required to be able to distinguish the input photon number. After the photon detection, Alice and Bob can determine whether the protocol is successful based on the photon detection results. Here, we only list the 16 successful detection results of Alice in Table
| Table 1.
The successful photon detection results of Alice. Here, the • means our protocol is successful under the detection result (each of the detectors registers exactly one photon). . |
Here, we take the detection results of D1aD2aD5aD6aD1b D2bD5bD6b each registering exactly one photon for example. Under the detection results, the whole-photon state |Φ3⟩AB ⊗|φ3⟩ will collapse to
Then, Alice and Bob make the photons in b4e4 modes pass through the PCS and the photons in c4f4 modes pass through the PCL. After that, the state |Φ4⟩AB will turn into
Finally, Alice makes the output photons in b5c5 modes pass through PBS10a and Bob makes the output photons in e5f5 modes pass through PBS10b. These operations make |Φ5⟩AB finally evolve to
If we get one of the other 255 successful detection results, we can also finally obtain the output state the same as |Φout⟩AB with the help of the phase-flip operation. Therefore, the total success probability for Alice and Bob obtaining |Φout⟩AB is
On the other hand, we consider the case in which the single photon is lost with the probability of 1 − F. Under this case, the input state is the vacuum state and the whole photon state is the auxiliary photon state |φ2⟩. After the auxiliary photons pass through the BSs, it can be found that only the item t|HSVL⟩b3 ⊗ t|HSVL⟩c3 ⊗ t|HSVL⟩e3 ⊗ t|HSVL⟩f3 can lead to successful photon detection results. In detail, after the BSs, such item will evolve to On the other hand, we consider the case in which the single photon is lost with the probability of 1−F. Under this case, the input state is the vacuum state and the whole photon state is the auxiliary photon state |φ2⟩. After the auxiliary photons pass through the BSs, it can be found that only the item t|HSVL⟩b3 ⊗ t|HSVL⟩c3 ⊗ t|HSVL⟩e3 ⊗ t|HSVL⟩f3 can lead to successful photon detection results. In detail, after the BSs, such item will evolve to
From Eqs. (
Until now, the entire amplification process is completed. When the protocol is successful, Alice and Bob will share a new mixed state
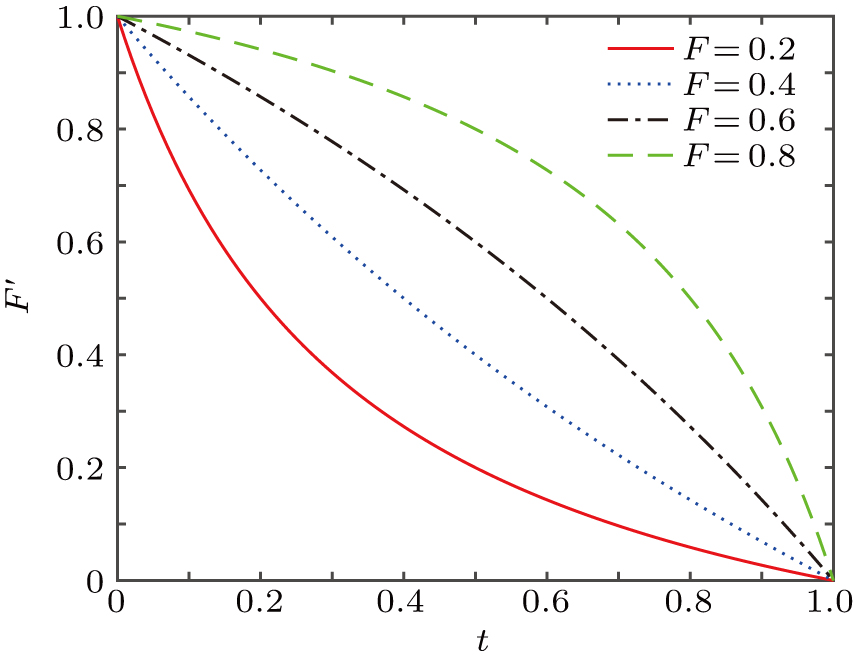
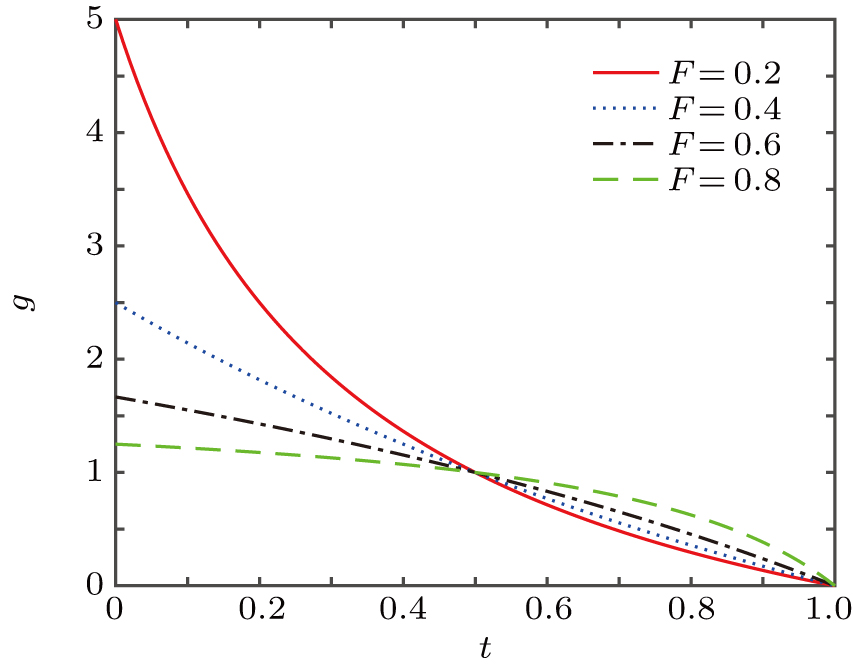
The fidelity F′ of the new mixed state does not relate to the four coefficients α, β, δ, and η, but is only determined by the fidelity F of the initial input mixed state and the transmittance t of the VBSs. We define the amplification factor g as
Interestingly, besides realizing the amplification of SPE, our protocol can be extended to resist decoherence in the spatial DOF. This means our protocol can simultaneously protect the SPE of the polarization–time-bin qudit from complete transmission photon loss and partial photon loss caused by environmental noise.
Here, we suppose that the photon source S generates a polarization–time-bin qudit with the form of |ψin⟩ in Eq. (
Our protocol can be extended to increase the fidelity of the target state, while recovering the two entanglement coefficients a and b to be the same. To achieve this goal, we only need to adjust the transmittance of the four VBSs. Here, we define the transmittance of VBS1a, VBS2a to be ta and that of VBS1b, VBS2b to be tb. If the single photon is not lost, after the BSs, the single photon state and auxiliary photon state can be written as
Here, by adjusting the two entanglement coefficients of the spatial modes to be the same, we can control the transmittance of the four VBSs to meet 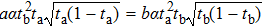
On the other hand, if the initial single photon is lost, by selecting the item corresponding to one of the 256 successful detection results, we can also obtain the vacuum state with the probability of
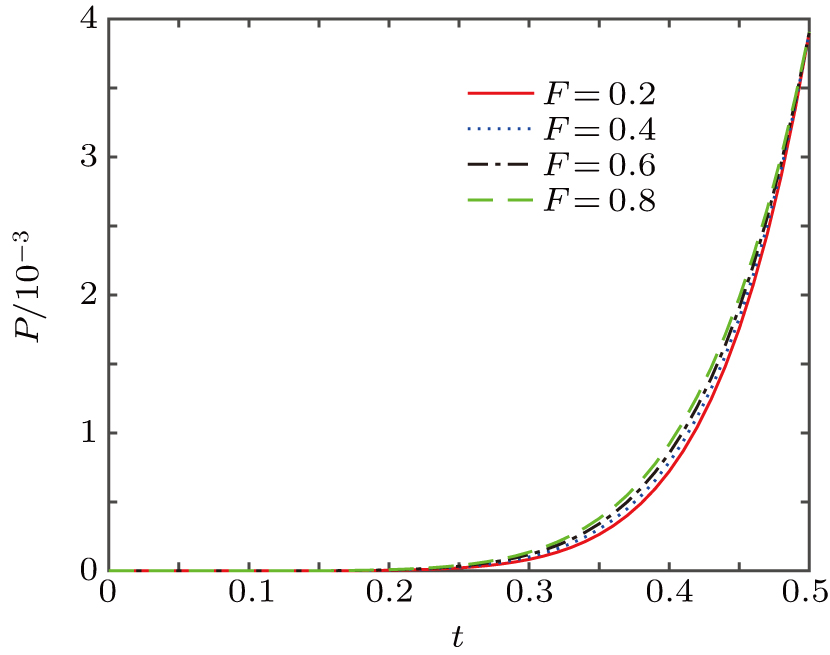
The total success probability can be calculated as
This paper mainly describes a simple and efficient amplification protocol for the SPE of an arbitrary polarization–time-bin qudit. This protocol only needs some auxiliary single photons in |H⟩ or |V⟩ polarization. After performing the protocol, we can judge whether the protocol is successfully heralded by the single-photon detection results. As long as the protocol is successful, we can effectively increase the fidelity of SPE by adjusting the transmittance of the VBSs. Moreover, after the amplification, the encoded polarization and time-bin features of the single-photon qudit can be well preserved and cannot be leaked to either Alice or Bob. This amplification protocol is based on linear optics, which can be implemented under the current experimental condition. Meanwhile, the distilled new mixed state with high fidelity can be retained and used in other applications. Moreover, we also discuss the application of our protocol by adjusting the transmittance of the four VBSs, and we can protect the SPE of the polarization–time-bin qudit from complete photon loss and partial photon {loss}, simultaneously.
It is important to discuss the fidelity F′, the amplification factor g, and the total success probability P of the protocol. From Eqs. (
In summary, we propose an efficient NLA protocol to protect the SPE of an arbitrary polarization–time-bin qudit assisted by some auxiliary polarized photons, some linear optical devices, and photon-number-resolving detectors. In this protocol, Alice and Bob individually perform similar operations in her/his location simultaneously. Each of them adopts some PBSs and Pockel cells to convert the original photon state into two polarization components, which will be individually amplified simultaneously. During the operation, with the help of a 50:50 BS and single-photon detection, the parties can judge whether the protocol is successful according to the photon detection results. When the protocol is successful, the parties can finally distill a new mixed state with higher fidelity by adjusting the transmittance of the VBS. The amplification protocol can be realized under current experimental conditions. Moreover, after the amplification, the encoded polarization and time-bin features of the single-photon qudit can be well preserved and cannot be leaked to either Alice or Bob. We also discuss the application of our amplification protocol to resist complete photon loss and partial photon loss problems during photon transmission. After the amplification, Alice and Bob can not only increase the fidelity of the target state, but also solve the decoherence problem. Based on the above features, our amplification protocol may be useful in the future quantum communication field.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] |