Skyrmion, as quasi particle spin structures, are protected by their topology.^[1] In the 1960s, Tony Skyrme first proposed skyrmion.^[2] In 2006, it was first proposed that there is a stable skyrmion structure in magnetic materials, which exists as a ground state.^[3] In 2009, skyrmion was first discovered in MnSi magnetic single crystal materials in an experiment.^[4] At present, skyrmions have been widely found in many materials such as the B20 structure MnSi, FeGe, Fe_1−xCo_xSi, Cu₂OSeO₃,^[1,5–7] and many ultrathin multilayer films with symmetry broken, such as Fe/Ir,^[8] Ta/CoFeB/MgO, Ir/Co/Pt, Pt/Co/MgO, Ta/CoFeB/TaO_x, Ir/Co/Pt, Ir/Co/Pt, etc.^[9–11] Skyrmion can be driven by electrical current at ultralow current density J = 10² A/cm².^[1,12] The topological nature can protect skyrmion from dissipating and fluctuating.^[12,13] Skyrmion can be applied to the next-generation spintronics devices, such as racetrack memory and spin-transfer nano-oscillators.^[12,14,15] Skyrmion has been realized in the multilayer films at room temperature.^[10,16,17] All these materials need a very strong Dzyaloshinskii–Moriya interaction (DMI).^[18,19] At present, theories and experiments have shown that skyrmion can be realized in magnetic materials without DMI.^[20,21]

Artificial skyrmion is another kind of skyrmion, which is stabilized at room temperature. Artificial skyrmion can be realized due to the exchange coupling between hard and soft magnetic layer. Ding et al.^[20] first predicted that artificial skyrmion can be realized in Co/CoPt bilayers. They found that artificial skyrmion can be deformed with an external magnetic field and the core diameter of the skyrmion can vary from 10 nm to 100 nm. Li et al.^[21] experimentally demonstrated the existence of artificial skyrmion in Co/Ni/Cu(001), and confirmed that the artificial skyrmion is stable at room temperature. Li et al.^[21] found that the stability of the skyrmion structure is higher than that of the vortex structure due to its topological nature. The artificial skyrmion can also be realized in Co/[Co/Pd]_n and Co/Pd.^[22,23] In their experiments, the diameter of the artificial skyrmion disk was about 1 μm.^[21,23] In practical application, the diameter of skyrmion is preferably close to 10 nm.^[9] Therefore, the diameter of the artificial skyrmion is too large for application.

In the film system with perpendicular magnetic anisotropy (PMA), the magnetic bubble or skyrmion can be realized from the competition between PMA and dipolar interaction.^[22,24] Recent experiments and theories have shown that artificial skyrmion has been realized in CoPt/Co bilayers.^[23] In the CoPt/Co bilayers, the vortex could be realized in soft magnetic layer Co, and the vortex structure in Co layer was imprinted into the CoPt layer with PMA, thus the artificial skyrmion was realized.^[20,22,23] CoCrPt is a high-density recording magnetic material with large PMA.^[25] The PMA constant K_CoCrPt of CoCrPt is 3.00 × 10⁵ J/m³. Meanwhile the process of preparing NiFe thin film by magnetron sputtering is very mature,^[26,27] and experiments and theories have shown that the vortex structure can be realized in NiFe thin film.^[28–30] Therefore, if there is a vortex structure in the NiFe layer, the vortex structure is imprinted into the CoCrPt layer, and then the artificial skyrmion can be realized in CoCrPt. By incorporating an additional CoCrPt layer, the dipolar field of the CoCrPt layer can tailor the diameter of the artificial skyrmion. Therefore, it is possible to realize artificial skyrmions of different diameters without external magnetic field.^[31]

In this paper, the micromagnetic simulations are performed based on the oommf code,^[32] and the artificial skyrmion is realized in CoCrPt/NiFe bilayers. The critical magnetic field (shown in Fig. 3) of the bilayers is simulated. It is found that the critical magnetic field of the core is lower than the critical magnetic field of the edge. The external magnetic field plays a key role in determining the core diameter of the skyrmion. The core diameter of the artificial skyrmion in CoCrPt/NiFe bilayers can vary from 10 nm to 120 nm. By this way, the CoCrPt/Cu/CoCrPt/NiFe four-layer film is constructed. In these four-layers, the core diameter of the artificial skyrmion can vary from 13 nm to 76 nm, which means that it is possible to obtain small diameter artificial skyrmion in experiment without an external magnetic field.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (a) NiFe(8 nm)/CoCrPt(10 nm) bilayers: top NiFe layer is disk, and bottom CoCrPt layer is square; (b) (CoCrPt(40 nm)/Cu(40 nm)/CoCrPt(10 nm)/NiFe (8 nm)) four-layer: bottom CoCrPt layer and Cu spacer layer are square with the same size as top CoCrPt layer.

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. (color online) (a) Hard magnetic layer and (b) soft magnetic layer magnetic moments’ distribution of the bilayers in skyrmion state, (c) magnetic moments’ distribution of CoCrPt layer in vortex state, (d) red and blue lines represent magnetization line profiles as marked with dash line in panels (b) and (c). The red and blue color denote spins downward-of-plane and out-of-plane direction respectively, and arrows denote the in-plane direction.

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. (color online) (a)–(j) Magnetic moments’ distribution of CoCrPt layer in relaxation state without magnetic field. Panels (a) and (f) are the same as panel (c) of Fig. 2, and panel (b) of Fig. 3, respectively, panel (h) is the same as panel (b) of Fig. 2. Panels (a), (c), (f), and (j) show vortex structure and panels (b), (d), and (h) exhibit skyrmion structure. Panels (g) and (i) show the unstable magnetic configuration with the magnetic field of −200 mT and 220 mT, respectively. Panel (e) shows critical magnetic field of core/edge (green / red line) as a function of soft magnetic layer diameter.

In this paper, the micromagnetic simulations were based on the oommf code.^[32] The material parameters used in this paper were PMA constant: K_CoCrPt = 3.00 × 10⁵ J/m³ and K_NiFe = 5.00 × 10² J/m³; saturation magnetization: M_CoCrPt = 3.98 × 10⁵ A/m and M_NiFe = 8.6 × 10⁵ A/m; exchange constant A_CoCrPt = 1.0 × 10⁻¹¹ J/m and A_NiFe = 1.30 × 10⁻¹¹ J/m. An interlayer exchange constant between NiFe and CoCrPt of 1.00 × 10⁻¹¹ m/J was also used.^[33,34] K_Cu, A_Cu, and M_Cu were all set to be zero. We focused on two multilayer nanodisk systems, as shown in Figs. 1(a) and 1(b). Figure 1(a) shows a CoCrPt(10 nm)/NiFe(8 nm) bilayer, the top layer is the NiFe with disk structure, and the diameter of the disk is 120 nm; the bottom layer is the CoCrPt with square structure, and the size is 160 nm × 160 nm. Figure 1(b) shows a CoCrPt (40 nm)/Cu(40 nm)/CoCrPt(10 nm)/NiFe(8 nm) four-layer. In all the simulations, the cell size was 2 nm × 2 nm × 2 nm. A Gilbert gyromagnetic ratio γ = 2.211 × 10⁵ m/A· s and Gilbert damping constant α = 0.5 were used, respectively.

Skyrmion can be realized by first applying a 400-mT magnetic field along the +Z direction to make all the magnetic moments flip in the +Z direction. When the external magnetic field is turned off, the NiFe disk relaxes to a vortex state as shown in Fig. 2(c). In Fig. 2(c), the top layer NiFe is vortex structure. Figures 2(a) and 2(b) show the top view of NiFe and CoCrPt magnetic configuration of the bilayers in skyrmion state, respectively. The system can be divided into three regions (regions 1, 2, and 3), as shown in Figs. 2(b) and 2(c). The spins in the regions 1 and 3 are in the Z or −Z direction. The spins of the CoCrPt beneath the NiFe layer (beneath-region, including regions 1 and 2) are the same as that of the NiFe layer. Figure 2(d) shows the magnetization line profile as marked in Figs. 2(b) and 2(c) with dash lines. Without special statement, the configuration is in relaxation state without external magnetic field and the magnetic configuration in this paper is CoCrPt layer, which is 2 nm away from NiFe layer surface. In this paper, as shown in Fig. 2(d), the core diameter of skyrmion is defined as the full width of half maximum (FWHM) value of the magnetization.

In the NiFe/CoCrPt bilayers, the PMA constant K_CoCrPt of the hard magnetic layer CoCrPt is large, so the spins in the region 3 are in Z or −Z direction (as shown in Fig. 3(d), in region 3, the magnetic moments’ distribution of vortex is the same as that in skyrmion); at the same time as shown in Fig. 3 (a), the soft magnetic layer is in vortex state, and the vortex structure can be mapped into the CoCrPt layer. The artificial skyrmion can be realized by the two-edge constriction. As shown in Figs. 3(a)–3(d), magnetic configurations are all in relaxation state with no external magnetic field. When the 200-mT external magnetic field is applied to the −Z direction in Fig. 3(a), region 2 turns over first, then region 1 turns over, finally we turn off the magnetic field. Artificial skyrmion can be realized as shown in Fig. 3(b). In the same way, when a 400-mT magnetic field is applied to the −Z direction in Fig. 3(b), the magnetic moments reverse from region 2 to region 3. Finally the magnetic field is turned off and the vortex state can be realized, as shown in Figs. 3(a) and 3(c), where their vortices are in the opposite Z-axis directions. In this way, as shown in Fig. 3, the conversion of two types of artificial skyrmions (Figs. 3(b) and 3(d)) can be realized, which is the same as the results of Co/CoPt bilayers.^[23] Figure 3(b) and 3(d) have the opposite skyrmion numbers 1 and −1, respectively.

The magnetic field is applied to the bilayers in vortex structure in the −Z direction as shown in Fig. 3(f). It is found that if the amplitude of magnetic field is large enough, region 2 turns over firstly as shown in Figs. 3(g) and 3(i). When we turn off the magnetic field, the vortex as shown in Fig. 3(j) or skyrmion as shown in Fig. 3(h) can be obtained, and Figs. 3(f) and 3(j) have the opposite Z-axis directions. The critical magnetic field of the core is the minus magnetic field for region 1 flipping. The critical magnetic field of the edge is the minus magnetic field for the region 3 flipping. The relationship between the critical magnetic field of the core or edge and the diameter of the soft magnetic layer is calculated. As shown in Fig. 3(e), when the diameter of the soft magnetic layer reaches about 148 nm, the vortex structure is unanimously reversed. As shown in Fig. 3(e), the critical magnetic field of the core is smaller than the critical magnetic field of the edge, which is different from the experimental result of Ref. [21] in Co/Ni/Cu(001) system. [In the simulation given by Li et al., the critical value of the core (6000 Oe) was much higher than that of the edge (800 Oe)].^[21] In the simulations and experimental results given by Li et al.,^[21] the direction of magnetic anisotropy was in plane, rather than in the Z direction, and the magnetic moments were more stable in the direction of plane. Therefore, the critical magnetic field of skyrmion core is larger than the critical magnetic field of the edge.

The in-plane magnetic moments are easier to reverse. The Beneath-Region increases with the diameter of the soft magnetic layer increasing. The magnetic moments in region 2 are deflected in the horizontal direction, so that the magnetic anisotropy energy significantly increases as the diameter of the soft magnetic layer increases and it is more likely to flip under the action of external magnetic field. Finally, the critical magnetic field of the core decreases. Meanwhile, region 2 decreases. This will reduce the difference between critical magnetic fields of the edge and core as shown in Fig. 3(e).

The magnetic moments can be deflected if external magnetic field is applied. When the in-plane magnetic field is applied to the skyrmion, the position of the skyrmion core changes and the structure of the artificial skyrmion is defor-med.^[1] Here, the magnetic field is applied to the bilayers (skyrmion structure and vortex structure) in the X direction.

The artificial skyrmion has excellent topological protection. As shown in Figs. 4(e), 4(f), and 4(g), the position of the red zone changes, and the structure of the skyrmion deforms. The displacement of the core in the Y direction increases with the magnetic field increasing. In the X direction, the core still has a slight displacement. When the applied magnetic field is about 76 mT, beneath-region changes into single domain as shown in Fig. 4(h), and it is higher than the Li et al.s’ reported value 13.5 mT (135 Oe) in Co/Ni/Cu(001) system.^[20] As shown in Figs. 4(i)–4(l), the in-plane magnetic field is applied to the vortex structure. The vortex structure deforms and the position of vortex–core changes. When the amplitude of external magnetic field is about 28 mT, beneath-region changes into the single domain. The critical magnetic field of the plane in Fig. 4(h) is much larger than that in Fig. 4(l), and the difference between the critical magnetic fields is the same as that given by Li et al. in Co/Ni/Cu(001).^[21]

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (color online) (a)–(d) Magnetization line profiles as marked with dash lines in panels (e)–(h), (e)–(l) magnetic moment’s distributions of CoCrPt under action of different values of Bx, where panels (e)–(h) are the artificial skyrmions for different applied fields, and panels (i)–(l) are the vertices for different applying fields.

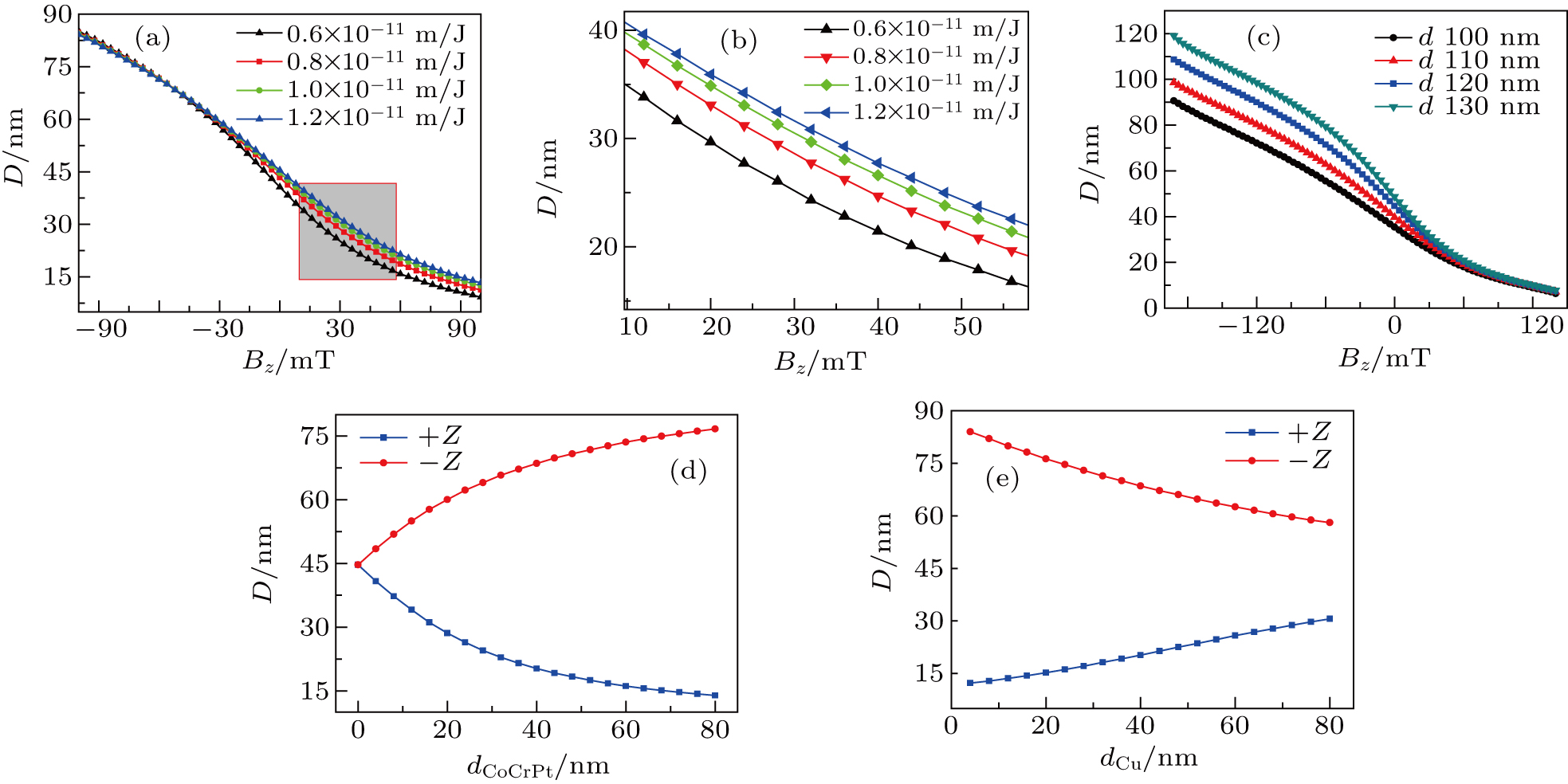
If an out-of-plane magnetic field is applied to skyrmion, then the diameter of the skyrmion changes. As shown in Fig. 2(b), the magnetic moment at the core is orientated along the −Z direction. Here, the magnetic field is applied to the skyrmion structure in the +Z direction. The core diameter of skyrmion decreases with magnetic field increasing (Fig. 5).

Fig. 5.

Figure Option ViewDownloadNew Window

Fig. 5. (color online) Plots of core diameter of skyrmion versus external magnetic field Bz ranging (a) from −90 mT to 90 mT, and (b) from 10 mT to 60 mT, for different interlayer exchange constants; (c) plots of core diameter of skyrmion versus external magnetic field Bz ranging from −180 mT to 130 mT for different soft magnetic layer diameters; (d) plots of core diameter of skyrmion versus thickness of bottom CoCrPt layer (CoCrPt(x nm)/Cu(40 nm)/CoCrPt(10 nm)/NiFe(8 nm)) ranging from 0 nm to 80 nm in +Z and −Z directions; (e) plots of core diameter of skyrmion versus thickness of Cu layer(CoCrPt(40 nm)/Cu(x nm)/CoCrPt(10 nm)/NiFe(8 nm)) ranging from 0 nm to 80 nm in +Z and −Z directions. Panel (b) shows an enlargement of the shadowed area in panel (a); In panels (d) and (e) the blue and red line represent the directions of the magnetic moment of the bottom CoCrPt in +Z and −Z directions, respectively, and all the direction of the skyrmion core is in the −Z direction.

The core diameter of the skyrmion as a function of perpendicular applied static field is simulated for different interlayer exchange constant. The four interlayer exchange constants (0.6 × 10⁻¹¹ m/J, 0.8 × 10⁻¹¹ m/J, 1.0 × 10⁻¹¹ m/J, 1.2 × 10⁻¹¹ m/J) are considered as shown in Fig. 5(a). It is found that when the external magnetic field is constant, the core diameter of the skyrmion does not change significantly with the interlayer exchange constant. The core diameter of the skyrmion is completely determined by an external magnetic field. However, when the external magnetic field is in the +Z direction as shown in Fig. 5(b), the core diameter of the skyrmion will be bigger when the interlayer exchange constant is larger. However, the biggest change caused by interlayer exchange constants (0.6 × 10⁻¹¹ m/J and 1.2 × 10⁻¹¹ m/J) is no more than 10 nm.

The influence of the diameter of the soft magnetic layer on the core diameter of the skyrmion is simulated. Figure 5(c) shows the plots of core diameter of the skyrmion versus external magnetic field for different diameters of the soft magnetic layer (100 nm, 110 nm, 120 nm, and 130 nm). The core diameter of the skyrmion decreases as the external magnetic field increases. When the external magnetic field is in the +Z direction, the core diameter of the skyrmion is almost unchanged for different diameters of the soft magnetic layer. When the external magnetic field is in the −Z direction, the core diameter of the skyrmion decreases as the diameter of the soft magnetic layer decreases.

The core diameter of skyrmion is almost determined by the external magnetic field, which varies from 10 nm to 120 nm. The diameter of skyrmion is basically consistent with the value in the diameter range calculated by Sun et al.^[20] and Miao et al.^[23] in Co/CoPt bilayers.

To find a smaller skyrmion structure, as shown in Fig. 1(b), the CoCrPt/Cu/CoCrPt/NiFe four-layer film is constructed. The top two layers CoCrPt and NiFe are 10 nm and 8 nm in thickness, respectively. All the direction of the magnetic moments of bottom CoCrPt are set to be in +Z or −Z direction. The bottom CoCrPt layer can generate dipole magnetic field,^[31] and this dipole magnetic field is applied to the artificial skyrmion through Cu layer due to interlayer coupling. Thus, artificial skyrmions with different diameters are obtained without the action of an external magnetic field.

The core diameter of skyrmion is simulated as a function of bottom CoCrPt layer or Cu layer thickness. As shown in Figs. 5(d) and 5(e), the blue or red line indicates that when the bottom CoCrPt magnetic moments are in +Z or −Z directions, core diameter of the skyrmion decreases or increases. Considering the condition of the bottom CoCrPt magnetic moments in +Z direction as shown in Fig. 5(d), when the thickness of bottom CoCrPt layer increases as the core diameter of the skyrmion decreases, and the minimum core diameter of the skyrmion is about 13 nm with an 80-nm-thick CoCrPt. Then, as shown in Fig. 5(d), the red line indicates that the maximum diameter of the skyrmion is about 76 nm. When the CoCrPt layer thickness continues to increase, the diameter of the skyrmion core does not change. This happens because the amplitude of the dipole magnetic field generated by bottom CoCrPt layer is limited.^[31] Considering the condition that the bottom CoCrPt magnetic moment is in the +Z direction as shown in Fig. 5(e), as the thickness of bottom Cu layer increases, the diameter of the skyrmion core increases. This happens because the interlayer coupling through Cu layer decreases as the Cu layer thickness increases.

Based on micromagnetic simulations and the material parameters of CoCrPt and NiFe at room temperature, skyrmion structure can be realized in NiFe (8 nm)/CoCrPt (10 nm) bilayers. The critical magnetic field of the core or edge of the skyrmion in NiFe (8 nm)/CoCrPt (10 nm) bilayers will decrease as the diameter of the soft magnetic layer increases, respectively. The artificial skyrmion in NiFe (8 nm)/CoCrPt (10 nm) bilayers has the excellent property of topological nature. The external magnetic field plays a key role in determining the core diameter of the skyrmion. A smaller skyrmion structure can be constructed through multilayer films, such as CoCrPt/Cu/CoCrPt/NiFe four-layer film. The core diameter of the skyrmion can be adjusted just by changing the thickness of bottom CoCrPt and Cu layer without changing external magnetic field. The artificial skyrmion in a CoCrPt/Cu/CoCrPt/NiFe four-layer film with a diameter of 13 nm is very suitable for the future applications.