† Corresponding author. E-mail:
Project supported by the National Basic Research Program of China (Grant No. 2016YFA0301903), the National Natural Science Foundation of China (Grant Nos. 11174370, 11304387, 61632021, 11305262, and 61205108), and the Research Plan Project of the National University of Defense Technology (Grant No. ZK16-03-04).
The dynamical decoupling (DD) method is widely adopted to preserve coherence in different quantum systems. In the case of ideal pulses, its effects on the suppression of noise can be analytically described by the mathematical form of filter function. However, in practical experiments, the unavoidable pulse errors limit the efficiency of DD. In this paper, we study the effects of imperfect pulses on DD efficiency based on quantum trajectories. By directly generating a pseudo noise sequence correlated in time, we can explore the performance of DD with different pulse errors in the typical noise environment. It shows that, for the typical 1/f noise environment, the phase error of operational pulses severely affects the performance of noise suppression, while the detuning and intensity errors have less influence. Also, we get the thresholds of these errors for efficient DD under the given experimental conditions. Our method can be widely applied to guide practical DD experimental implementation.
Dynamical decoupling (DD), inspired by the application of Hahn echo in nuclear magnetic resonance,[1] is one approach widely used to maintain quantum coherence in various kinds of systems. By exerting a pulse sequence in the quantum evolution process, this method introduces a rapid, time-dependent control field to reduce the interaction with the environment. It was formally introduced in a general way by Viola,[2,3] explaining how a pulse sequence is arranged to compensate the noise effect. After that, several concrete protocols were proposed for different purposes, including periodic DD,[2,3] Carr–Purcell–Meiboom–Gill (CPMG),[4,5] Uhrig DD,[6] and so on. In recent years, different DD protocols have been experimentally demonstrated to preserve the coherence of qubits in trapped ions,[7,8] including the superconducting quantum circuit,[9] electron spins,[10,11] atomic ensembles,[12] semiconductor quantum dots,[13,14] and nitrogen vacancy centers in diamond.[15]
Ideal DD involves a sequence of instantaneous perfect π pulses as the control field, which are used to modulate interaction with the environment. With a tailed pulse sequence, this method can suppress certain frequency components of noise, and its effects can be theoretically described by filter functions. Based on this noise filtering mechanism, qubits can also be used as quantum sensors to detect environment noise.[16] However, unavoidable errors in operational pulses always exist in practical experiments. Even small imperfections, including deviations of pulse width, rotation angle and axis, can have a severe impact on the decoupling efficiency after the accumulation of numerous pulses, which has been pointed out in several works.[8,17–22] Since the pulse errors destroy the symmetry of the DD modulation, we cannot describe this process using concise analytical form like the filter function. Therefore, we use a numerical method to quantitatively analyze the DD process with imperfect pulses.
In this paper, we numerically generate the noise sequence with time correlation according to its power spectral density (PSD).[23] Based on the noise generation, we utilize the quantum trajectory method to numerically study the impacts of imperfections. Different types of pulse error can be directly simulated in the given noise environment to study their effects on DD. The simulated results illustrate that in a typical noise environment, such as 1/f noise, phase errors have more influence than detuning and intensity errors and error thresholds decrease with the rise of the pulse number. With these results, we now know how pulse errors influence the DD process in certain environments and this method therefore allows us to instruct various kinds of practical experiments.
The structure of this article is arranged as follows. In Section
In this section, we give the analytical model for ideal DD by simply reviewing the results of Ref. [8]. In the DD operation, there are various kinds of protocols for sequence arrangement. Without loss of generality, the model here is based on the widely used CPMG sequence.[4,5]
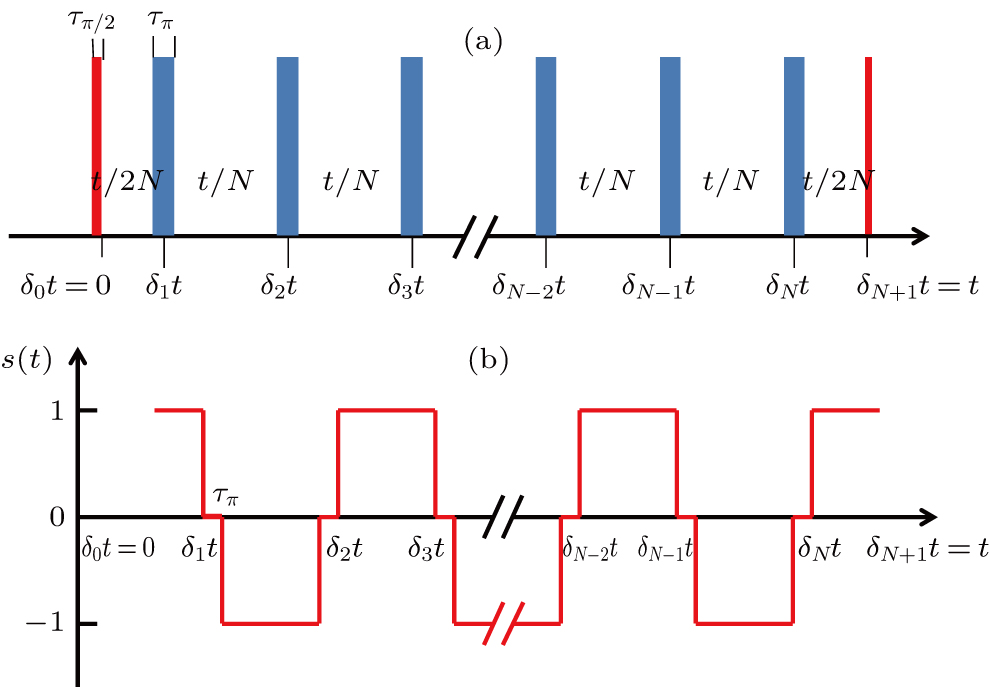
The noise suppression effect of DD is usually checked by a modified Ramsey process, with a number of instantaneous π pulses inserted between a pair of Ramsey π/2 pulses.[24] Particularly, the sequence arrangement of the CPMG protocol is demonstrated in Fig. 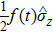
After the first π/2 pulse, the initial state |0〉 is prepared to the superposition state 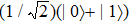
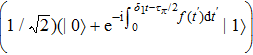


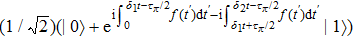
The state in Eq. (

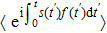

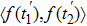
Introducing the PSD p(ω) of noise, which is the Fourier transform of 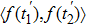
The above theoretical model and filter function are derived from ideal pulses, in which case the noise accumulation direction can be described by a concise and symmetrical jump function s(t). However, the imperfections of the pulse will destroy this symmetry, leading to difficulty in obtaining the analytical results. In addition, the imperfections are hard to describe and the accumulation of hundreds of pulses would make the theory form extremely complex. Therefore, a numerical method is required to replace the theoretical model, because it can simulate noise and pulse errors directly, obtaining the evolution results on a large scale of the ensemble average.
In this section, we develop a numerical method for imperfect DD based on the quantum trajectory method. It should be emphasized that, to conveniently consider the time correlation characteristics of the ambient noise, we adopt a semi-classical model to describe the noise.
The quantum trajectory method, also known as the quantum jump method or quantum Monte Carlo wave function method, is one option to simulate quantum dissipation in an open system.[26] The main principle of this method is to evolve the system wave function in time with a pseudo-Hamiltonian, simulating randomization in every time step. The whole process of figuring out one result is called one quantum trajectory and the final result is the ensemble average of many trajectories. To simulate imperfect DD with this method, we must construct the numerical pulse error model and generate the noise sequence.
In the interaction picture and rotating wave approximation, the typical Hamiltonian of a two-level system with pulses in DD can be expressed as
As is known, any unitary transformation of the qubit state can be described as a rotation of the Bloch vector on the Bloch sphere, U = exp(ik)Rn(θ), where exp(ik) is a term about the global phase and Rn(θ) is the rotation operator which has a specific form:
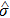
In this numerical simulation tool, pulse errors are introduced in the form of parameter fluctuations of pulse detuning, intensity, and phase. Each parameter is fixed in every simulation time step and fluctuates in different time steps. The fluctuations are considered as random terms added to the standard parameter in the simulation. It is shown from Eq. (
In the numerical simulation, every trajectory means the evolution with one possible noise sequence. The corresponding evolution includes the unitary evolution of Hd with environmental noise and Hi with parameter fluctuations in pulses. The parameter fluctuations are white noise with different standard deviations, while the environmental noise is generated as a noise sequence according to its PSD which is assumed here or obtained from the experiment. To generate it, we discretize the PSD by sampling in its majority range and create frequency spectrum random variables.[22] Then the noise sequence is generated by Fourier transformation into the time domain. Here we choose a typical 1/f noise with its PSD p(f) = 50000/[1 + (f/1000)2] to generate a noise sequence and test its effectiveness by PSD estimation.
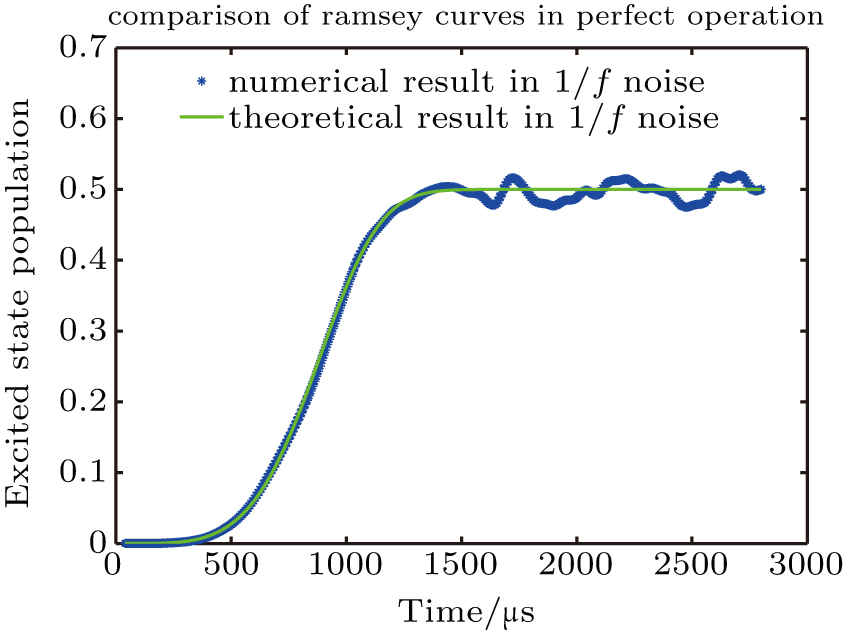
In this comparing simulation, we set the ensemble amount as 200. Each trajectory represents a whole Ramsey process with a given noise sequence. Through the trajectory average, this numerical tool simulates the real physical system to the most extent. In the 1/f noise environment, the Ramsey process with no pulse is simulated in Fig.
To study the impact of pulse errors, we add parameter fluctuations to pulse physical parameters, including detuning, phase, and intensity, which directly influence the coupling strength. The quality of pulses is determined by these pulse parameters and they are set based on general experimental conditions. In the physical parameter arrangement, we assume π pulse detuning δ to be 0 Hz, phase ϕ to be 0, and coupling strength Ω, as well as Rabi frequency, to be 106 Hz. In the simulation, number of quantum trajectories is 1000 and we get the ensemble average as the final result. With regard to the noise environment, we choose 1/f noise because it is one typical type of noise in the experiment. The 1/f noise mainly focuses on the low-frequency components because such noise derives from the fluctuations in electronic devices. Here we adopt a general 1/f noise form, with its PSD p(f) = a/[1 + (f/f3)n]. Most frequency components and energy is focused within the low-frequency range while only a small proportion of noise power is distributed in the high-frequency range. Therefore, we choose one specific form of PSD p(f) = 50000/[1 + (f/1000)2] to guarantee that most power is concentrated within the low-frequency range. In the simulation, we assume parameter fluctuations to be white noise and Gaussian distributed. Different levels of the standard deviation of parameter fluctuation are set on pulse detuning, phase, and coupling strength. They are written as σδ, σϕ, and σΩ respectively. With this numerical simulation tool, we explore the general influence of these pulse error sources. But for specific experiments, environmental noise should be detected as a prerequisite and then the particular influence of imperfections can be analyzed to direct the experiment.
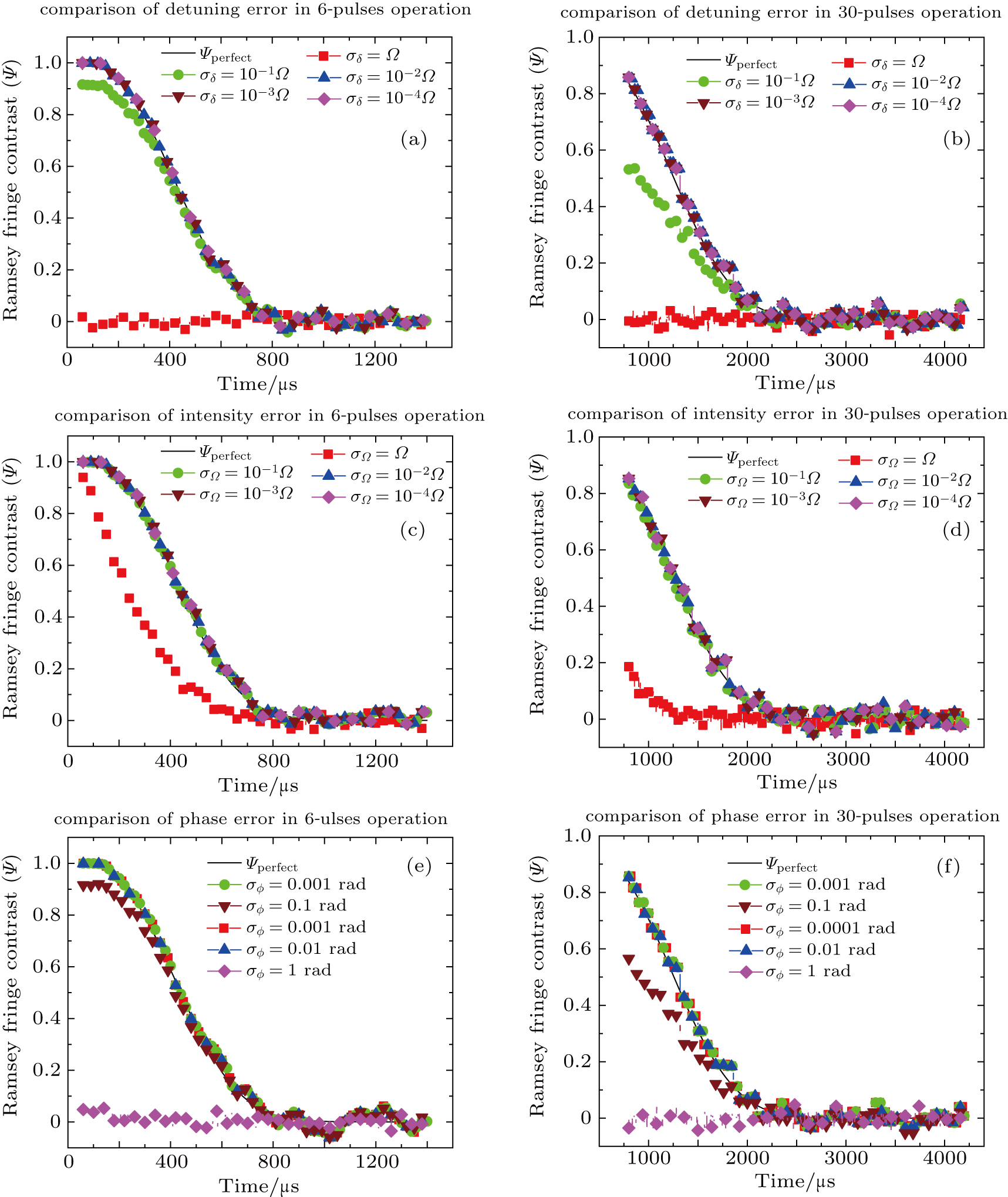
We simulate parameter fluctuations of detuning, phase, and coupling strength with 6 and 30 pulses respectively to compare the effects of error accumulation. In consideration of the current experimental developments, we simulate the imperfect DD sequences containing 6 and 30 pulses, which correspond to the cases of short coherence time qubits and relatively long coherence time qubits respectively. With regard to various parameter fluctuation sources, we set different stages based on different σδ, σϕ, and σΩ on each source to consider how errors influence decoherence. In the simulation, different standard derivations are set in the form of ratio value to Ω. We calculate the Ramsey fringe contrast of every curve and consider the qubit to become decoherent when the fringe contrast is below 1/e, at about 0.37. For convenience, we simplify the Ramsey fringe contrast as Ψ. According to Eq. (
First we introduce detuning fluctuations and compare their impacts with different pulse accumulation in Fig.
As phase errors almost determine the length of coherent time, much caution should be applied on this parameter. The preciseness of the pulse phase should be stressed particularly in pulse control. Its electronic error that causes phase instability should also be eliminated completely. Fluctuations in detuning and coupling strength have similar impacts on the evolution process. This is partially because their fluctuation range is tiny compared to the energy level and coupling strength. But it also depends on the real experimental conditions. As a result, we can conclude that the phase noise is the most important error source in the Ramsey process.
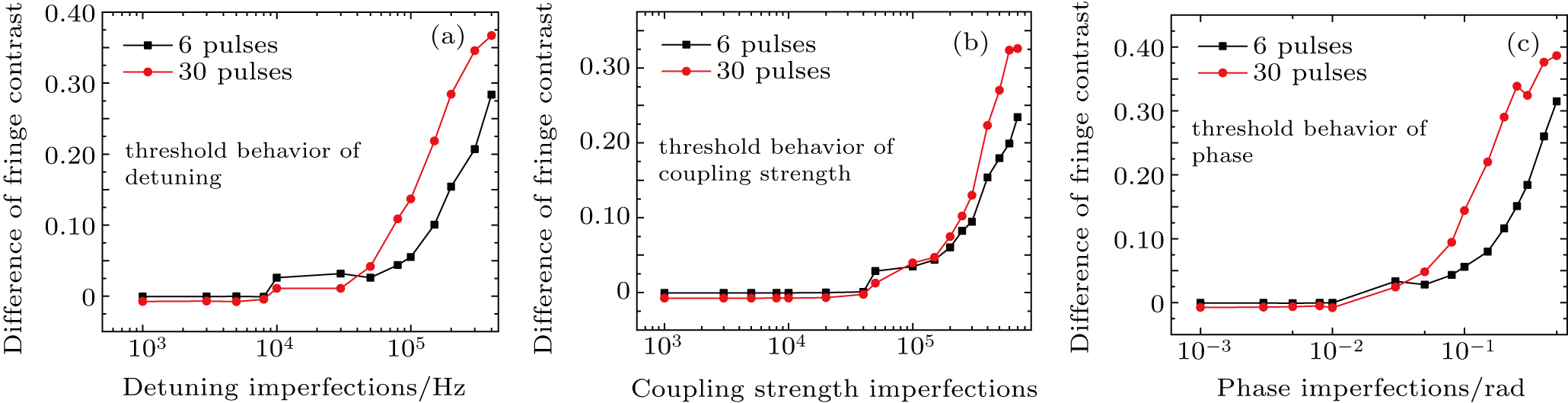
The threshold of different kinds of imperfections with different pulse numbers is one important parameter in the experimental implementation. We can compare the fringe contrast between the case of perfect pulses and imperfect pulses with various amounts of fluctuations to get the threshold. As we have defined before, the time when the analytical fringe contrast is around 0.37 is the coherence time. At this time, we observe the fringe contrast of other simulated results and calculate the difference from 0.37. This difference indicates the decoherence caused by pulse imperfections. We can also state that the imperfections have no obvious effects on decoherence if the difference is less than 0.05. The detailed comparison of detuning, intensity or coupling strength, and phase imperfections is shown in Fig.
The simulation of pulse imperfections is beneficial to instruct the experimental practice. Our simulation can reveal the thresholds of pulse errors in detuning, intensity, and phase under certain experimental conditions. In practical experiments, the frequency drift, fluctuation in the power of lasers, and phase fluctuation induced by various sources can be monitored as parameter fluctuations. When these fluctuations exceed their thresholds, they are inclined to induce decoherence. The results of the simulation indicate which part of the laser parameters need to be improved and to what extent they need to be optimized. For this reason, we are able to guarantee the efficiency of the DD operation.
We have demonstrated the application of CPMG, for one specific sequence, in the Ramsey process. This process can be completely described by the theory of filter function, which is determined by the pulse number, time interval between pulses, and pulse operation time. In this process, the quality of pulses is fundamental for the final result as an accumulation of pulse errors would destroy the coherence. Due to the fact that it is difficult to calculate the influence of pulse imperfections, we adopt a numerical method to generate noise to build a numerical tool for the simulation of the Ramsey process. According to the PSD of the noise environment, it is reliable to simulate the whole Ramsey process with the DD sequence. We assume a typical 1/f noise environment and simulate the Ramsey process with fluctuations of the pulse parameters. Generally, the quantum state is robust to intensity and detuning errors but extremely sensitive to phase noise. In addition, through simulation, we know the thresholds of the fluctuations of these physical parameters of the pulse. Some improvements can be made to the pulses to reduce fluctuations below the threshold value. Therefore, this simulation tool guides us in improving the experiment, especially when environmental noise is roughly detected by a spectral analyzer. If the pulse noise is designed in the simulation, the results could be an important reference to the real experiment.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] |