Effects of imperfect pulses on dynamical decoupling using quantum trajectory method
Project supported by the National Basic Research Program of China (Grant No. 2016YFA0301903), the National Natural Science Foundation of China (Grant Nos. 11174370, 11304387, 61632021, 11305262, and 61205108), and the Research Plan Project of the National University of Defense Technology (Grant No. ZK16-03-04).
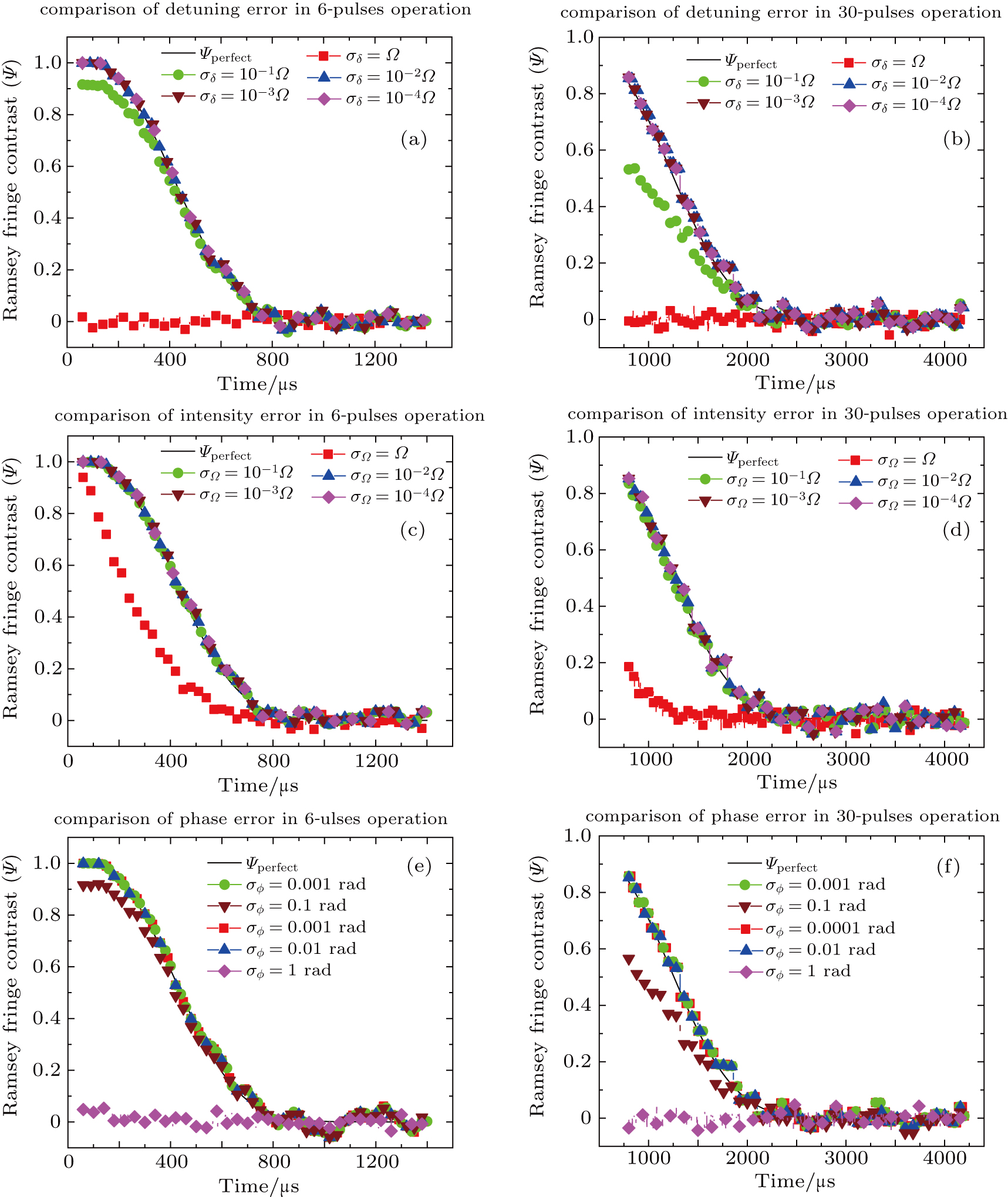
(color online) (a) and (b) Ramsey fringe contrast with detuning fluctuations in 6 pulses and 30 pulses. We set a series of σδ as 10−4Ω, 10−3Ω, 10−2Ω, 10−1Ω, and Ω. In the 6-pulse situation, the simulated results of σδ that are within 10−2Ω fit well with the perfect results. When σδ equals 10−1Ω, the simulated result deviates from the perfect result, while for σδ = Ω, the qubit becomes decoherent at the beginning. In the 30-pulse situation, the coherent time is prolonged by more pulses. On the other hand, the simulated curves do not fit well with the perfect curve like that in the 6-pulse situation because of the error accumulation. As is shown, for σδ within 10−2Ω, the results nearly remain the same as the perfect result. For σδ = 10−1Ω, the qubit tends to be more liable to dephase than in the situation of 6 pulses. Therefore, the detuning deviation thresholds are approximately 10−1Ω for the 6-pulse operation and tend to be lower than 10−1Ω for the 30-pulse operation. (c) and (d) Ramsey fringe contrast with intensity fluctuations in 6 and 30 pulses. σΩ varies among 10−4Ω, 10−3Ω, 10−2Ω, 10−1Ω, and Ω. The coherent time of the perfect operation in 6 pulses and 30 pulses is similar to the detuning situation. For the 6-pulse and 30-pulse situations, when σΩ does not exceed 10−1Ω, the simulated results fit well with the perfect results, but the derivations of the 30-pulse situation are amplified because of the error accumulation. In the 6-pulse situation, the curve of σΩ = Ω is deviates notably from the perfect results, while this trend is exaggerated in the 30-pulse situation. The threshold of fluctuation in pulse intensity is a little below Ω according to these two figures. (e) and (f) Impacts of phase fluctuations with 6 and 30 pulses compared with the perfect operation. We set a series of σϕ as 1 rad, 0.1 rad, 0.01 rad, 0.001 rad, and 0.0001 rad. For Ramsey fringe contrast (Ψ) with 6 pulses in different deviation groups, when σϕ is less than or equal to 0.01 rad, the phase error seems to be less influential on the decoherence and fits well with the perfect results. When σϕ is 0.1 rad, the simulated curve is slightly deviated from the perfect pulse curve. For σϕ = 1 rad, the qubit becomes completely decoherent in the beginning. In the situation of 30 pulses, the influence of errors is notably amplified compared to that with 6 pulses. The qubit is more sensitive to phase noise. When σϕ exceeds 0.1 rad, the coherence is destroyed completely. In addition, for a σϕ of 0.1 rad, the curve is split from the perfect situation clearly. The thresholds of both situations are a little below 0.1 rad.