The carrier transport behavior under intrinsic and extrinsic electric field, generally, dominate the performance of many optoelectronic devices, such as solar cells,^[1] voltage-dependent resistors,^[2] piezoelectric sensor,^[3] X/γ-ray detector,^[4] etc. However, the carrier transport is critically affected by the actual electric field distribution. Of particular interest within this class of devices are X/γ-ray detectors. Factors which determine the electric field distribution, are metal contacts and grown-in defects, especially the planar defects such as twin boundaries. Besides its significant fundamental interest, understanding the physics of planar defects is essential to enable the engineering of better devices. It may also advance the knowledge of grain boundaries in other corresponding devices, e.g., the grain boundaries in ZnO varistors^[5–7] and polycrystalline solar cells.^[1,8]

Cadmium zinc telluride, as a leading room-temperature X/γ-ray semiconductor detector material, has received much attention for its potential applications in environmental monitoring, nuclear medicine, industrial nondestructive testing, etc.^[9–12] However, its wide deployment is hindered by the poor uniformity of the charge collection properties in today’s commercial CdZnTe material. Since twin boundary is one of the major causes of these charge-transport non-uniformities in CdZnTe detectors, which made today’s CdZnTe low yield and high price.^[13,14] Moreover, the electric field distribution near twin boundaries is not thoroughly understood at present. This is mainly because of X/γ-ray detectors are working at high electric field strength (thousands V/cm), whereas commonly applied modern characterization methods, i.e., scanning capacitance microscopy,^[15] Kelvin probe force microscopy,^[8,16] and EBIC imaging,^[17] only cover a range of micrometers or a few volts. The depleted and inverted grain boundary models were mainly proposed by such techniques.^[8,15,16]

The pulsed laser-induced transient current technique^[18,19] allows us to access the twin boundary dominated charge transport behavior in the CdZnTe detectors. The information on the electric field can also be obtained from the analysis of charge drift transient in response to excitation of the crystal.^[20] Li et al.^[21] suggested that a nonuniform electric field exists at the two sides of the grain boundary within the CdZnTe detector. However, this method cannot directly determine the electric field distribution in crystals which have planar defects, since it requires the uniform distribution of traps for the carriers and a constant drift velocity under a constant internal electric field, which is not a realistic assumption for such devices.

Besides, Pockels effect measurement (PE)^[20,22,23] is a simple and reliable technique for evaluating a crystal’s uniformity prior to their use in detector fabrication. Unfortunately, two crystalline grains separated by a twin boundary inevitably have two different orientations, a fact which hardly allows resolving the electric field distribution from PE images. Therefore, a bicrystal planar device with a special orientation has to be fabricated enabling a direct measurement of the electric-field distribution. Babalola et al.^[24] observed the nonuniform electric field distribution at twin boundary in CdMnTe detector by this method. To the best of our knowledge, there has been few study on the direct observation of electric field distribution at twin boundary in CdZnTe detectors. Moreover, a complete understanding of the electric field evolution as a function of bias at twin boundaries is lacking. As far as this fundamental problem is concerned, the utilization of CdZnTe crystal with twin boundaries are limited.

In this work, the carrier transport behavior and internal electric field distribution in a CdZnTe bicrystal with a {111}–{111} twin boundary was systematically studied using pulsed laser induced transient signals and Pockels effect measurements. Furthermore, an energy band model was proposed to elucidate the electric field distributions associated with the twin boundary.

The indium-doped Cd_0.9Zn_0.1Te crystals (n-type) with the resistivity over 10⁹ Ω · cm were grown by the modified vertical Bridgman method in Imdetek Ltd.^[25] One typical sample with a {111}–{111} twin plane inside is cut into dimensions of 5 × 5 × 5 mm³. The Electron backscatter diffraction (EBSD) map can be seen in the Supporting Information 1 (SI1). After polishing and etching, Au electrodes were fabricated on two opposite surfaces using vacuum evaporation, with a thickness of about 50 nm. The infrared (IR) transmission imaging was applied to observe the distribution of Te inclusions and related extended defects.

The carrier transport process of CdZnTe detectors has been investigated by pulsed laser induced transient current technique (TCT). The experiment setup used for TCT is illustrated in the previous report.^[26] The distribution of the internal electric field in the CdZnTe detector was investigated by PE technique, whose schematic experimental setup is shown in Fig. 1(a). The detector was positioned between two crossed linear polarizers. The schematic of the CdZnTe detector was presented in Fig. 1(b). A collimated tungsten lightbulb with a 980-nm IR filter (FWHM = 10 nm, transmittance of 86% at peak maximum) uniformly illuminated the detector, which is parallel to the contact, i.e., perpendicular to the applied field. A pair of 90° orthogonally orientated polarizing filters are arranged at either side of the sample, with the transmitted light imaged by an IR-enhanced digital charge-coupled device (CCD) camera. An Ortec 556 was employed as a high-voltage power supply to bias the crystal.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (color online) Experiment setups. (a) Schematic of the PE measurement setup and (b) the CdZnTe detector; (c), (d) IR transmission images with the IR light is parallel to the 〈111〉 direction in panel (c) and perpendicular to 〈111〉 direction in panel (d).

Under these conditions and according to the direction of the applied electric field with respect to the crystal orientation, for each (x, y) point of the detector, the intensity I(x, y) of the transmitted light depends on the mean electric field distribution E(x, y) along the optical path, through the relation^[27]

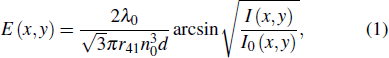Twin planes decorated by Te inclusions are often observed in CdZnTe crystals.^[29,30] Figure 1(c) shows a plane of Te inclusion across the twin boundary observed parallel to the 〈111〉 direction. Figure 1(d) shows Te inclusions observed on the {111}–{111} twin plane. It is noted that the region near the twin boundary (∼ 0.5 mm each side) is nearly free of Te inclusions which may be attributed to migration and diffusion of droplets and excess atoms toward these energetically favorable sinks.^[31] Far away from this twin boundary region, Te inclusions uniformly distributed with an area density of 500 inclusions/cm² (see SI 2). The twin boundary and its induced defects should affect the carrier transport process.

To investigate the distortion of the carrier transport process affected by the twin boundary, we recorded the pulsed laser-induced transient currents. The information on the electron drift process in a semiconductor can be derived by analysis of the shape and width of the current pulses of such transient current technique. In this configuration, the width of the current pulse reflects the electron drift time across the device, and hence a probe of the electric field distribution according to the relation

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (color online) Laser-induced transient currents under the bias of +500 V and +1000 V, respectively, at room temperature. The inset is a schematic diagram of the setup for the transient current measurements.

Since the vicinity of the twin boundary is nearly free of Te inclusions, this region may have higher electron mobility. To further confirm that such peaks were mainly induced by the nonuniform electric field distribution, we employed PE to investigate the internal electric distribution of the device. Initial measurements of the electric field distribution were carried out using a bias voltage up to 1800 V. In Fig. 3, we present the images of the light intensity distribution profiles of the biased detector from ±300 V up to ±1800 V in steps of 300 V. The lighter portions of the profile are clearly associated with the high levels of light transmission. According to Eq. (1), the intensity of the images directly indicates the electric distribution profiles. The intensity of crossed-polarized light increases as the bias is raised, revealing the expected enhanced electric field. Here, we observed a buildup of an electric field in the vicinity of the twin plane, because of the intensity at such a location is much brighter than the rest of the sample. The positions of the brighter region relative to the twin plane are depended on the applied voltages.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Light intensity distribution profiles of the bicrystal at different voltages. The left side is biased and the right side is grounded.

To further clarify the effect of the twin boundary on the electric field distribution, figure 4(a) shows the contour map of the internal electric field depending on the bias and the distance from the biased surface to the grounded surface after image processing. These profiles clearly demonstrate that the electric field is non-uniformly distributed between the cathode and the anode, especially near the twin boundary. The nonuniform electric field distribution can be seen clearly. A higher electric field region located close to the twin boundary is observed. The higher electric field around the region of the twin plane changes its position from the left side to the right side of the twin boundary as the bias changes its polarity from negative to positive. The brighter region, i.e., the region of higher electric field intensity exists at the lower potential side of the crystal. With the bias increased, the higher electric field zone is expanded, from 0.2 mm (300 V) to 1.2 mm (1800 V) as can be seen in Fig. 4(a). Figure 4(b) also shows the line profiles of electric field distribution at the applied bias of −1800 and +1800 V, respectively. The insets are the corresponding PE images at applied bias of 1800 and +1800 V, and the position of the electric field in Fig. 4(b) is indicated by the red lines. The highest electric field is over 6 kV/cm, which is much higher than the expected average internal electric field (3.6 kV/cm, see the dashed line in Fig. 4(b)). The width of this distortion is about 1.2 mm, which is much wider than the region with twin boundary and the decorated Te inclusions.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (color online) Electric field distribution in CdZnTe device. (a) The contour map of electric field distribution profile extracted from the PE images at various applied bias. (b) The electric field distribution profiles at −1800 V and 1800 V. Inset is the PE images (5 × 5 mm2), correspondingly.

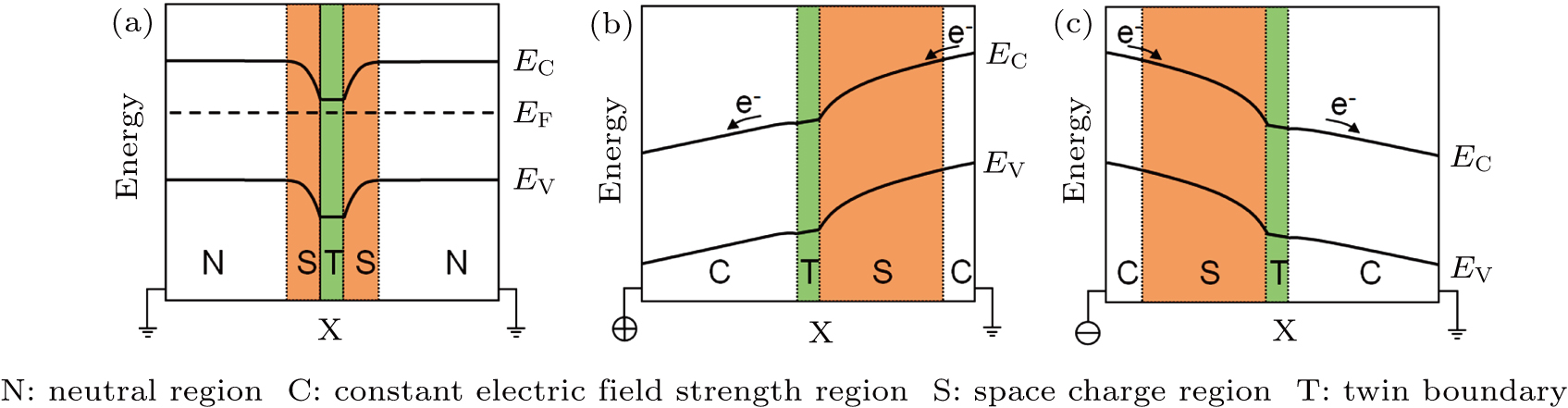
An energy band model is proposed to understand the variation of the internal electric field at different bias. Defects at the twin boundary (i.e., Te inclusions and the induced dislocations, etc.) and the enrichment of impurities will produce a more conductive layer at the grain boundary compared to the interior crystal.^[32–34] As a consequence, an n–n⁺–n junction forms at the twin boundary, as illustrated in Fig. 5(a). The bottom of the conduction band bends down towards the Fermi level in the vicinity of the boundary, creating two space charge regions and back-to-back potential barriers at either side. The width of the space charge region would depend on the conductivity of the grain and the concentration of donor states at the grain boundary. Without bias, there is a negative electric field at the left side of the twin boundary and a positive electric field at the right side. The build-in voltage of an n–n⁺ junction is given by , where V_t is the thermal voltage, and N_d are donor concentrations at the n⁺-type region and n-type region. Therefore, the potential barrier height of the junction is relatively small, about several tenths of an eV. Different donor concentration between the two regions also results in that almost the entire space charge layer extends into the low-doped region of the junction. Moreover, the carrier concentration must be continuous in a homojunction thus the n⁺-type region is not completely depleted. In our experiments, the width of the extended space charge layer in the n-type region can be observed to change remarkably under different applied bias.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. (color online) A sketch of the proposed energy-band model of the negative space charge region at the twin boundary at (a) zero bias, (b) positive voltage on the left contact, (c) negative voltage on the left contact.

When a bias is applied to the sample, the potential energy barrier becomes asymmetric as shown in Figs. 5(b) and 5(c), corresponding to two possible polarities of the applied bias. The barrier height is generally governed by the interface state density of the twin boundary, which captures free carriers, leading to an interface charge. This interface charge is balanced by a corresponding bulk space charge of the depletion layer in the n-type region. When a positive voltage is applied on the left contact, the bias-induced electric field will weaken the original internal electric field at the left side of the twin boundary and strengthen the right one, as shown in Fig. 5(b). Under this condition, the left potential barrier is forward biased and the right potential barrier is reversed biased. As a result, the right space charge region expands as the positive voltage raises and the left one shrinks. Because the original potential barrier height is relatively small (several tenths of an eV) and the applied bias is high, the left barrier is easy to overcome and the electric field on the left side is almost a constant under sufficiently high bias. This is exactly what is observed in Figs. 3 and 4(a). When a negative voltage is applied at the left contact, the whole scheme is reversed, as shown in Fig. 5(c). This is clearly seen in Figs. 3 and 4(a).

We have performed the electric field distribution in a 5 mm CdZnTe X/γ-ray detector with a {111}–{111} twin boundary using the Pockels effect measurement. The electric field distribution distorted by the twin boundary is directly identified, which is responsible for the suddenly intensified signal in the carrier drift process of pulsed laser-induced transient current. The vicinity of the twin boundary is nearly free of Te inclusions, which promotes the electron drift velocity in the local area. A higher electric field region exists at the lower potential side of the twin boundary in the crystal, which expands with the bias increasing, from 0.2 mm (300 V) to 1.2 mm (1800 V). The highest disturbed electric field is over 6 kV/cm, which is much higher than the expected average 3.6 kV/cm. To understand the nonuniform electric field distribution, a model based on the formation of an n–n⁺–n junction across the twin boundary was proposed. Furthermore, this work provides a reference for the understanding of grain boundary devices based on charged grain boundaries.