† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 21573094, 11274142, 11474131, 11574112, and 51502109), the National Found for Fostering Talents of Basic Science, China (Grant No. J1103202), the Science Challenging Program (Grant No. JCKY2016212A501), and China Scholarship Council (CSC) during a visit of Ning Sui (Grant No. 201706175038) to MPIA is also acknowledged.
The energy dissipation mechanism of energetic materials (EMs) is very important for keeping safety. We choose nitrobenzene as a model of EM and employ transient absorption (TA) spectroscopy and time-resolved coherent anti-stokes Raman scattering (CARS) to clarify its energy dissipation mechanism. The TA data confirms that the excited nitrobenzene spends about 16 ps finishing the twist intramolecular charge transfer from benzene to nitro group, and dissipates its energy through the rapid vibration relaxation in the initial excited state. And then the dynamics of vibrational modes (VMs) in the ground state of nitrobenzene, which are located at 682 cm−1 (v1), 854 cm−1 (v2), 1006 cm−1 (v3), and 1023 cm−1 (v4), is scanned by CARS. It exhibits that the excess energy of nitrobenzene on the ground state would further dissipate through intramolecular vibrational redistribution based on the vibrational cooling of v1 and v2 modes, v1 and v4 modes, and v3 and v4 modes. Moreover, the vibration–vibration coupling depends not only on the energy levels of VMs, but also on the spatial position of chemical bonds relative to the VM.
The interest in the energetic material has increased rapidly in the last three decades. It is one type of important functional materials and plays an important role in the fields of military affairs and civilian engineering.[1] Therefore, people have paid much attention to understand the reaction mechanism, so as to further employ the energetic materials. The previous report[2] shows that the macroscopic properties of energetic materials are much sensitive to the physical and chemical processes on the atomic or molecular scale and are also dependent on the excitation conditions. According to the special characteristics of energetic materials, the energy dissipation mechanism is very important to improve the safety and properties of energetic materials.[3] However, this process covers from femtosecond to nanosecond time scales and is much dependent on the relaxation of excited state and the damping oscillation of chemical bonds.[4] Besides the relaxation between the electronic states, the vibrational cooling and vibration–vibrational coupling also participate in the energy dissipation through intramolecular vibrational redistribution (IVR)[5] or multi-phonon up-pumping,[6] even though the energetic materials are located on the ground state. These complex dynamic processes would affect the excess energy redistribution in the energetic materials, which would induce the cleavage of the reaction bond and release chemical energy of energetic materials.[7] This finally affects the explosion rate and the reaction products. Therefore, it is very important to clarify the energy dissipation mechanism of energetic materials in detail. However, the most test technique for energetic materials could not offer the kinetic information, such as the relaxation of energy state or the vibrational cooling. Fortunately, transient absorption (TA) technique and the time-resolved coherent anti-Stokes Raman scattering (CARS) technique are two types of important ultrafast spectroscopy techniques. The former would offer the kinetic relaxation of materials in the excited state and the latter would clarify the vibration cooling and vibration–vibration coupling of chemical bonds. Therefore, we believe that the dissipation mechanism of energetic materials would be clarified by employing the TA and CARS. Among these energetic materials, the energetic materials with nitro unit are frequently used for a variety of applications.[8–10] So, we select nitrobenzene as a model object and discuss the energy dissipation mechanism of energetic materials by considering its energy dissipation between electronic states and that of vibrational modes together.
In this work, we study the energy dissipation process of nitrobenzene by employing transient absorption technique which detects the energy dissipation between electronic states, and time-resolved coherent anti-Stokes Raman scattering technique which tracks vibration relaxation dynamics among different vibrational modes in nitrobenzene. As a result, the relaxation between electronic states and the dynamics among vibrational energy levels are both disentangled in detail. Our results originated from TA and CARS would help us to understand the energy dissipation process of nitrobenzene at great length.
Briefly, we employ a mode-lock Ti:sapphire femtosecond laser system (Coherent), which offers 2.6 mJ, 130-fs pulses at 800 nm with a repetition rate of 500 Hz. The output of the femtosecond laser beam is split into two parts by a beam splitter (9:1); the major one is frequency-doubled by a 1-mm thick beta barium borate (BBO) crystal to generate 400-nm pulses, which will be used as the pump pulse, while the minor one is focused into a 5-mm quartz cell filled with water to generate a white light continuum as the probe pulse. The excitation pulse (400 nm) is sent to a delay line and modulated by a synchronized optical chopper (Terahertz Technologies Inc., C-995) with a frequency of 250 Hz and used as the pump beam to excite the sample. The excitation spot is about 0.3 mm in diameter. The TA spectrum is carried out by a spectrometer (AvaSpec-2048 × 16). The time-resolved CARS system setup is shown in Fig.
The transient absorption (TA) is employed to probe the photo-excitation relaxation process of nitrobenzene. The nitrobenzene does not emit photons after photo-excitation, suggesting that the excited nitrobenzene would release its energy non-radiatively. Meanwhile, the excess energy originated from photo-excitation would heat up the nitrobenzene.[13] Figure
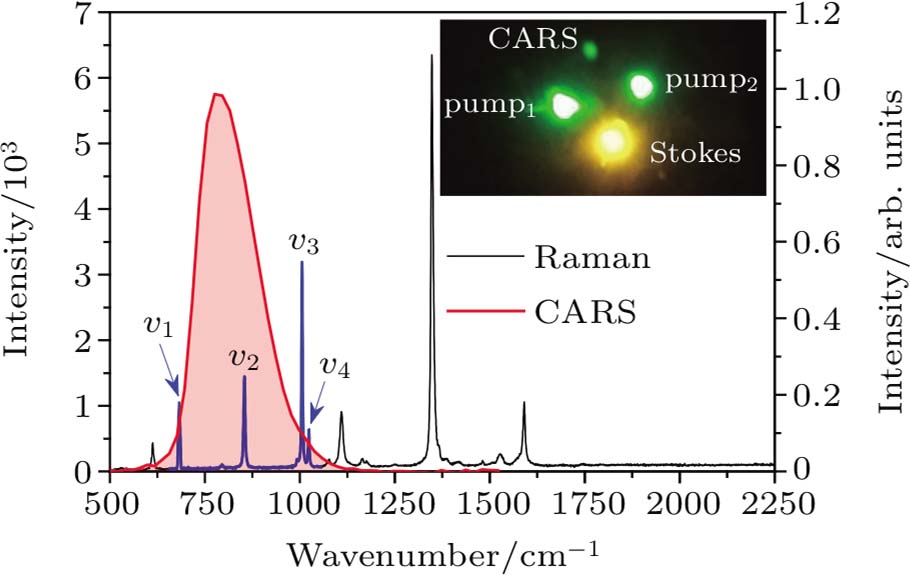
After the excited nitrobenzene relaxes on the ground state, the excess energy on the ground state would further dissipate through the vibrational dynamic behaviors involving the IVR or the vibration–vibrational coupling (VC). Therefore, the time-resolved CARS is employed to track the vibrational dynamics. Figure
| Table 1. Theoretical and experimental values of Raman shift (in unit cm−1) of nitrobenzene.[19] . |
For a better understanding of the relationship of vibration modes appearing in CARS spectrum, figure
In summary, these data allow us to draw a detailed map of the relaxation pathways of excited nitrobenzene. It is found that the excited nitrobenzene has to spend about 16 ps carrying out structural twist to finish the intramolecular charge transfer from benzene to nitro group. Simultaneously, the excited nitrobenzene also dissipates its energy through the rapid vibration relaxation. After that, the nitrobenzene in the TICT state would relax to the ground state. Then, dynamics of vibrational modes in the ground state of nitrobenzene located at 682 cm−1 (v1), 854 cm−1 (v2), 1006 cm−1 (v3), and 1023 cm−1 (v4), is scanned by time-resolved CARS, which are all distributed on the benzene ring. Since the distance between the chemical bonds corresponding to these vibration modes is very close, the couplings of v4 and v3, v2, and v1, and v4 and v1 really exist, which would influence the intramolecular energy redistribution. The IVR process depends not only on the energy level but also on the spatial position of chemical bonds relative to the vibration mode.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] |