Speckle reduction by selective spatial-domain mask in digital holography

Cite this Article

Liang Ming-Da, Chen Li, Hu Yi-Hua, Lin Wei-Tao, Chen Yong-Hao. Speckle reduction by selective spatial-domain mask in digital holography. Chinese Physics B, 2018, 27(10): 104202 Copy to clipboard

Permissions

Speckle reduction by selective spatial-domain mask in digital holography

Liang Ming-Da, Chen Li^†, Hu Yi-Hua, Lin Wei-Tao, Chen Yong-Hao

School of Physics and Opto-Electronic Engineering, Guangdong University of Technology, Guangzhou 510006, China

† Corresponding author. E-mail: ggchenli@gdut.edu.cn

Project supported by Guangdong Provincial Science and Technology Plan Project of China (Grant Nos. 2015B010114007 and 2014B050505020).

Abstract

An improved method of using a selective spatial-domain mask to reduce speckle noise in digital holography is proposed. The sub-holograms are obtained from the original hologram filtered by the binary masks including a shifting aperture for being reconstructed. Normally, the speckle patterns of these sub-reconstructed images are different. The speckle intensity of the final reconstructed image is suppressed by averaging the favorable sub-reconstructed images which are selected based on the most optimal pixel intensity sub-range in the sub-holograms. Compared with the conventional spatial-domain mask method, the proposed method not only reduces the speckle noise more effectively with fewer sub-reconstructed images, but also reduces the redundant information used in the reconstruction process.

PACS: 42.40.-i;42.30.-d;42.30.Ms;42.30.Wb

Keyword:digital holography;speckle reduction;spatial-domain mask

Show Figures

1. Introduction

Compared with the traditional holography, digital holography has many distinct advantages, such as higher imaging speed.^[1] Most importantly, the quality of the reconstructed image can be improved by the digital image processing technology. Recently, digital holography is widely applied to particle tracking,^[2] deformation measurement,^[3,4] holographic microscopy,^[5,6] biological cell monitoring,^[7] ultrafast recording,^[8] and so on. However, the speckle noise seriously affects the signal-to-noise ratio and spatial resolution of the reconstructed image,^[9] and limits the application of digital holography. Several effective methods have been proposed to reduce the speckle intensity and its size. For example, Uzan et al. proposed a non-local mean filter method that could reduce the speckle intensity by weighted averaging the intensity of a reconstructed image, but the measure of similarity lacks robustness.^[10] Massig et al. proposed a synthetic aperture digital holography to reduce the speckle size, but it required to record multiple holograms, which was not suitable for real-time processing.^[11,12]

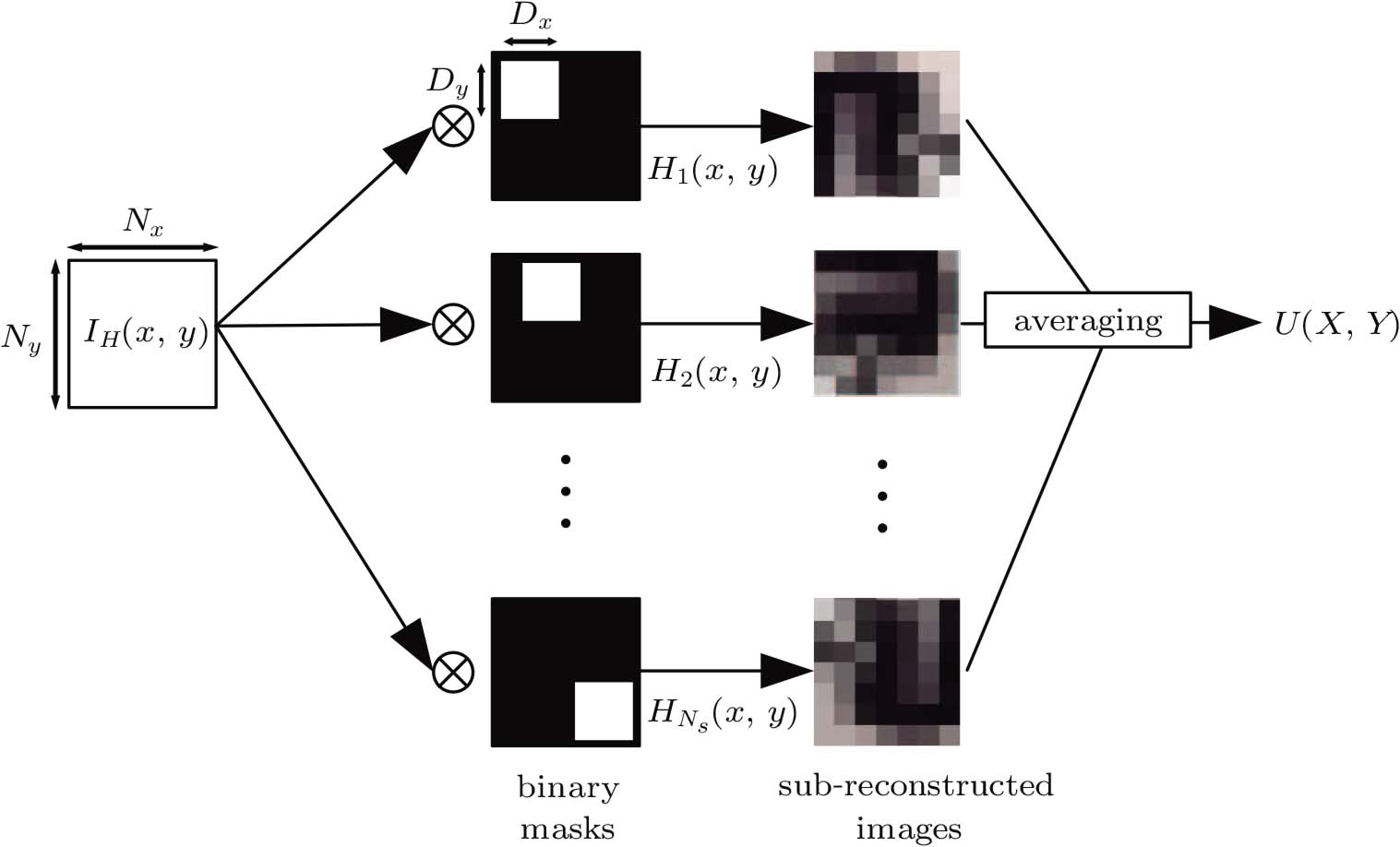
Maycock et al. proposed a discrete Fourier transform method to obtain multiple reconstructed images with different speckle noise patterns by moving the band-pass filter. However, this method cannot get enough different speckle patterns.^[13] Fukuoka et al. proposed a spatial domain mask (SDM) method to reduce the speckle intensity and improve the spatial resolution of the reconstructed image.^[14,15] The original hologram was filtered by the binary masks including a shifting aperture, then these sub-holograms were reconstructed. The speckle intensity can be reduced effectively by averaging all the sub-reconstructed images. However, it is obvious that averaging all the sub-reconstructed images without any selective standard is not the best strategy in this method. Therefore, an improved method is proposed in this paper, which can better reduce speckle intensity with fewer sub-reconstructed images.

2. Principle

As shown in Fig. 1, x₀y₀ is the object plane, xy is the plane where the charge-coupled device (CCD) is located, i.e., the hologram plane, and x′y′ is the reconstructed plane. The original hologram recorded by CCD is given by

where O(x,y) and R(x,y) denote the object light and the reference light in the hologram plane, respectively.

	Figure Option View Download New Window
	Fig. 1. The optical path diagram of an off-axis digital hologram.

3. Speckle reduction method

3.1. Spatial-domain mask method

The procedure of SDM method is performed in Fig. 2. A digital hologram recorded by charge-coupled device is filtered by the binary masks including a shifting aperture.^[16] The speckle patterns of these sub-reconstructed images are different because these images are reconstructed from different areas of the original hologram. By averaging all of the sub-reconstructed images, we can get a speckle-reduced reconstructed image.

	Figure Option View Download New Window
	Fig. 2. Schematic diagram of SDM method.

The improved reconstructed image base on SDM method is given by

where H_i (x,y) denotes the binary mask, N_S denotes the number of the sub-reconstructed images, and Fr{ } denotes the numerical Fresnel diffraction integral.

The total number of pixels in the original hologram is N_x × N_y. All of the sub-holograms have the same size as that of the original hologram, but the total number of the meaningful pixels in the sub-hologram is equal to the size of the aperture, i.e., D_x × D_y.

The total number of the sub-hologram is given by

where d_x and d_y denote the shift intervals of the mask aperture by rows and columns, and ⌊⌋ denotes that the function is rounded down.

In the SDM method, all of the sub-reconstructed images are accumulated without any selective standard, leading to the redundant information in the final reconstructed image and the quality of the image is not good enough.

3.2. Selective SDM method

Based on the deficiencies of the SDM method described above, we propose a selective SDM method. Compared to the original method, the proposed method adds a process of selecting favorable sub-reconstructed images.

According to the theory of digital holography, it is known that each pixel on the hologram has recorded all the information of the object. Therefore, the intensity of each pixel is closely related to the quality of the reconstructed image, and there may be a certain number of pixels within a specific range of intensity values, which are most related to the quality of sub-reconstructed image. The following analysis illustrates this point. This specific range is defined as the optimal pixel intensity range. For different objects or experimental environments, the optimal pixel intensity ranges on the hologram will be different.

The range of pixel intensity values in the hologram recorded by CCD is [0, 255]. In this process, our aim is to select the most optimal pixel intensity sub-range in [0, 255]. In order to select the optimal pixel intensity sub-range, we divide the range into multiple small sub-ranges first, such as

The speckle intensity of the sub-reconstructed images can be evaluated by the equivalent number of looks (ENL), which is given by

where ⟨I⟩ and σ denote the average values and the standard deviation of the reconstructed image, respectively. A higher ENL is desirable.

We assume that P_[m,n] is the proportion of the pixels whose intensity value is in the sub-range [I_m,I_n] in the total pixels (D_x × D_y), and it is given by

Then, we calculate the value of P_[m,n] and ENL in a sufficient amount of sub-reconstructed images (over 1000), and get the following data set: {ENL¹,ENL²,…,ENL¹⁰⁰⁰,…},

,…,

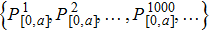
The correlation coefficient between ENL and P_[m,n] is given by

where Cov(ENL, P_[m,n]) is the covariance between ENL and P_[m,n], Var[ENL] is the variance of ENL, and Var[P_[m,n] is the variance of P_[m,n].

If ρ(ENL, P_[i,j]) = max ρ(ENL, P_[0,a]), ρ(ENL, P_[a,b]),…, ρ(ENL, P_[x,255]), it is shown that the change in the total amount of pixels whose intensity value is within the range [I_i,I_j] is most relevant to the change in the quality of sub-reconstructed image. So, the pixel intensity sub-range [I_i,I_j] is the most optimal pixel intensity sub-range. The sub-reconstructed images with a high value of P_[i,j] are the preferred sub-reconstructed images.

4. Experimental results

The experimental setup is shown in Fig. 3. The He–Ne laser (632.8 nm) is used as the light source. The split ratio of the beam splitters (BS, BS2) is 1:1. The pixel size of CCD is 4.65 μm × 4.65 μm, and the pixel amount is 960 × 1280. The objects are dice and coin.

	Figure Option View Download New Window
	Fig. 3. Experimental light path.

The reconstructed images without any speckle reduction method are shown in Fig. 4.

	Figure Option View Download New Window
	Fig. 4. The reconstructed images without any noise reduction. (a) The object is dice; (b) the object is coin.

During the experiment, based on the two improved methods, the size of the aperture is chosen as 480 × 640, 240 × 320, and 120 × 160, and the shifting interval is 20 pixels by rows or columns. 1500 sub-holograms are selected randomly.

Firstly, we divide the range [0, 255] into these small ranges as [0,50], [50,100], [100, 150], [150, 200], and [200, 255]. The distributions of ENL and P_[0,50]−P_[200,255] are shown in Fig. 5.

	Figure Option View Download New Window
	Fig. 5. (color online) The distributions of ENL and P_[0,50]−P_[200,255] from 1500 sub-reconstructed images. The black, red, green, blue, yellow, and magenta lines represent ENL, P_[0,50], P_[50,100], P_[100,150], P_[150,200], and P_[200,255], respectively. (a) The object is dice; (b) the object is coin. The vertical axis has been quantified for better comparison.

The correlation coefficient between ENL and P_[m,n] is given by Eq. (6). From the ENL and P_[0,50]−P_[200,255] in Fig. 5(a), we can get ρ(ENL, P_[0,50]) = 0.6886, ρ(ENL, P_[50,100]) = 0.4404, ρ(ENL, P_[100,150]) = −0.6796, ρ(ENL, P_[150,200]) = −0.6450, and ρ(ENL, P_[200,255]) = −0.5767.

It is obviously that ρ (ENL, P_[0,50]) > ρ (ENL, P_[50,100]) > ρ (ENL, P_[200,255]) > ρ (ENL, P_[150,200]) > ρ (ENL, P_[100,150]).

So, we choose the sub-range of [0,50] in the case of dice.

From the ENL and P_[0,50]−P_[200,255] in Fig. 5(b), we can get ρ (ENL, P_[0,50]) = 0.3066, ρ (ENL, P_[50,100]) = 0.5526, ρ (ENL, P_[100,150]) = 0.6370, ρ (ENL, P_[150,200]) = − 0.6404, and ρ (ENL, P_[200,255]) = −0.6337. And ρ (ENL, P_[100,150]) > ρ (ENL, P_[50,100]) > ρ (ENL, P_[0,50]) > ρ (ENL, P_[200,255]) > ρ (ENL, P_[150,200]).

So, we choose the sub-range of [100,150] in the case of coin. Then we divide the sub-ranges of [0,50] and [100,150] into smaller sub-range respectively as [0,10], [10,20], [20,30], [30,40], [40,50] and [100,110], [110, 120], [120, 130], [130, 140], [140, 150].

The distributions of ENL and P_[0,10]−P_[40,50] in the case of dice are shown in Fig. 6(a), and the distributions of ENL and P_[100,110] − P_[140,150] in the case of coin are shown in Fig. 6(b).

Figure Option
View Download New Window

Fig. 6. (color online) The distributions of ENL and P_[m,n] from 1500 sub-reconstructed images. (a) The object is dice. The black, red, green, blue, yellow, and magenta lines represent ENL, P_[0,10], P_[10,20], P_[20,30], P_[30,40], and P_[40,50], respectively. (b) The object is coin. The black, red, green, blue, yellow, and magenta lines represent ENL, P_[100,110], P_[110,120], P_[120,130], P_[130,140], and P_[140,150], respectively. The vertical axis has been quantified for better comparison.

In the case of dice, from the ENL and P_[0,10]−P_[40,50] in Fig. 6(a), we can get ρ (ENL, P_[0,10]) = 0.6745, ρ (ENL, P_[10,20]) = 0.6955, ρ (ENL, P_[20,30]) = 0.7083, ρ (ENL, P_[30,40]) = 0.6837, and ρ (ENL, P_[40,50]) = 0.6456, and ρ (ENL, P_[20,30]) > ρ (ENL, P_[10,20]) > ρ (ENL, P_[30,40]) > ρ (ENL, P_[0,10]) > ρ (ENL, P_[40,50]).

So, we choose the sub-range of [20, 30] in the case of dice. And in the case of coin, from the ENL and P_[100,110]−P_[140,150] in Fig. 6(b), we can get ρ (ENL, P_[100,110]) = 0.6494, ρ (ENL, P_[110,120]) = 0.6488, ρ (ENL, P_[120,130]) = 0.6329, ρ (ENL, P_[130,140]) = 0.5854, and ρ (ENL, P_[140,150]) = 0.3579, and ρ (ENL, P_[100,110]) > ρ (ENL, P_[110,120]) > ρ (ENL, P_[120,130]) > ρ (ENL, P_[130,140]) > ρ (ENL, P_[140,150]).

So, we choose the sub-range of [100,110] in the case of coin.

Finally, we sort the sub-reconstructed images following the order of P_[20,30] or P_[100,110], corresponding to dice and coin from the maximum value to the minimum value. And then, we accumulate the sub-reconstructed images in order. The ENL of the final reconstructed image varying with the sequence number of the sub-reconstructed images is shown in Fig. 7. As shown in Fig. 7, the red, green, and blue lines correspond to three kinds of apertures of 480 × 640, 240 × 320, and 120 × 160, respectively. The solid line corresponds to the proposed method, while the dotted line corresponds to the SDM method.

	Figure Option View Download New Window
	Fig. 7. (color online) ENL alters as the number of sub-reconstructed images increases. The red, green, and blue lines represent apertures of 480 × 640, 240 × 320, and 120 × 160, respectively. The solid line and the dotted line represent the proposed method and the SDM method, respectively. (a) The object is dice; (b) the object is coin

As revealed in Fig. 7, the solid line is rising fast, and generally higher than the dotted line. In addition, the highest value of each dotted line is at the rightmost point, while the highest point of the solid line moves to the left as the aperture is gradually reduced. It means that the proposed method can reduced the speckle intensity of the reconstructed image more quickly and effectively. Moreover, comparing to the SDM method, it is not needed to average all sub-images to obtain the reconstructed image with weaker speckle. The highest value of ENL on each line and the corresponding number of sub-reconstructed images are shown in Table 1.

Table 1.

The largest ENL and the corresponding number of sub-reconstructed images.

As revealed in Table 1, compare to the SDM method, the largest ENL is higher in the proposed method, while the corresponding number of sub-reconstructed image is smaller. This means that comparing to the SDM method, fewer sub-images are needed to obtain the reconstructed images with weaker speckle in the proposed method. The difference between the two methods will become more apparent as the aperture shrinks. The final reconstructed images are shown in Fig. 8.

	Figure Option View Download New Window
	Fig. 8. Final reconstructed images using dice and coin. (A1)–(A3): proposed method; (a1)–(a3): SDM method; (B1)–(B3): proposed method; (b1)–(b3): SDM method.

Comparing Fig. 8(A3) with 8(a3) and Figs. 8(B3) with 8(b3) respectively, we can see that when the aperture size is too small and the number of sub-reconstructed images is huge, the reconstructed image in the SDM method (Figs. 8(a3) and 8(b3)) will blur the border due to redundant information. And from Fig. 8, we also can see that the improvement of reconstructed image quality is more obvious in the small aperture, but when the aperture is large, this improvement is not obvious. The reason is that when the aperture increases, the value of P_[20,30] or P_[100,110] will become smaller, and the advantage of this method will be insignificant.

The highest value of P_[20,30] and P_[100,110] in all of sub-holograms is shown in Table 2.

Table 2.

The highest value of P_[20,30] and P_[100,110] in three kinds of apertures.

In order to compare the proposed method and SDM method more clearly, we analyze the final reconstructed images from two aspects of edge preservation index (EPI) and the intensity distribution of the pixels.

The EPI indicates the lateral or vertical edge holding ability after image processing.^[16] It is given as

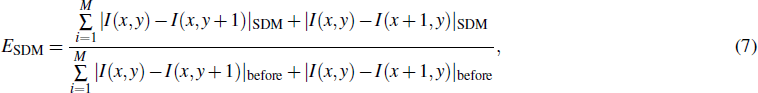
where M denotes the total number of reconstructed image pixels, I(x,y) denotes the intensity of pixels on the reconstructed image, E_SDM and E_proposed denote the edge preservation index of these two kinds, and the higher the better. The values of E_SDM and E_proposed from Figs. 8(A3), 8(B3), 8(a3), and 8(b3) are shown in Table 3.

Table 3.

The values of E_SDM and E_proposed.

From Table 3, we can see that the E_proposed values in Figs. 8(A3) and 8(B3) are higher than the E_SDM in Figs. 8(a3) and 8(b3), respectively. It means that the proposed method can better maintain the edge of the reconstructed image. Besides, in the case where the aperture is 120 × 160, the intensity distributions of all pixels in the final reconstructed images of both methods are shown in Fig. 9.

	Figure Option View Download New Window
	Fig. 9. (color online) The intensity distribution of all pixels in the final reconstructed images. (A3), (a3), (B3), and (b3) are corresponding to (A3), (a3), (B3), and (b3) in Fig. 8, respectively. The vertical axis represents the sum of pixels on the corresponding intensity value. For better comparison, the horizontal axis has been quantified.

In Fig. 9, the blue part represents the background or the dark areas of the object, the green part represents the zero-order image, and the red part represents the bright area of the object. Comparing Figs. 9(A3) with 9(a3), we can see that the red part moves closer to the left in Fig. 9(A3), which means that in the reconstructed images, there are fewer pixels with excessive high brightness. However, in the proposed method (Fig. 9(A3)), there are more pixels with appropriate brightness, and the same is true between Figs. 9(B3) and 9(b3). Therefore, compared to the SDM method, the proposed method can avoid blurring the details caused by the excessive high brightness of the reconstructed images.

5. Conclusion

In order to reduce the speckle intensity of reconstructed images, the conventional SDM method averages all sub-images and obtains a reconstructed image with weak speckle intensity. However, when the number of sub-images is huge, the reconstructed image will blur the border due to excessive redundant information. An improved method is proposed to deal with this problem well. In this method, the sub-hologram in which the pixel intensity changes gently will be chosen, and then reconstructed as well as averaged to obtain a higher-quality reconstructed image with weaker speckle. The experimental analysis shows that the number of the required sub-images is greatly reduced and the speckle intensity of the reconstructed image is weaker.

Reference

[1]	Chen L Ma X Wang Q 2012 Opt. Eng. 51 5802
[2]	Chang X Zeng Y Lei H Yao C Lu J Hu X 2017 Acta Opt. Sin. 37 0812002 in Chinese
[3]	Gao X Y Wang Y H Li J R Dan X Wu S Yang L 2017 Opt. Eng. 56 066107
[4]	Zhou B W Wu X C Wu Y C Yang J Gréhan G Cen K F 2013 Acta Phys. Sin. 62 204203 in Chinese
[5]	Igarashi A Komori T Tamaki T Arimoto H Fukuda T Watanabe Q 2017 Opt. Eng. 56 111702
[6]	Kamlund S Oredsson S 2017 Cancer Res. 77 909
[7]	Wang H Y Yu M J Jiang Y N Song X F Zhu Q F Liu F F 2013 Acta Phys. Sin. 62 244203 in Chinese
[8]	Prozorov T Almeida T P Kovács A Dunin-Borkowski R E 2017 J. R. Soc. Interface 14 20170464
[9]	Wang D T Wang Y X Guo S Rong L Zhang Y Z 2014 Acta Phys. Sin. 63 154205 in Chinese
[10]	Uzan A Rivenson Y Stern A 2013 Appl. Opt. 52 195
[11]	Massig J H 2002 Opt. Lett. 27 2179
[12]	Zhang Q S Lu X X Yu Q T Liu G Y 2009 Chin. Phys. 18 2764
[13]	Maycock J Hennelly B M Mcdonald J B Frauel Y Castro A Javidi B Naughton T J 2007 J. Opt. Soc. Am. 24 1617
[14]	Mori Y Fukuoka T Nomura T 2015 J. Opt. 17 125706
[15]	Fukuoka T Mori Y Nomura T 2016 J. Disp. Technol. 12 315
[16]	Zhang W Sun R H Zhang X C 2004 Remote Sensemote Sensing Inform. 4 4