† Corresponding author. E-mail:
Project supported partially by the National Key Research and Development Program of China (Grant No. 2016YFB1000902), the National Natural Science Foundation of China (Grant No. 61472412), and the Program for Creative Research Group of the National Natural Science Foundation of China (Grant No. 61621003).
In this paper, we focus on two-qubit pure state tomography. For an arbitrary unknown two-qubit pure state, separable or entangled, it has been found that the measurement probabilities of 16 projections onto the tensor products of Pauli eigenstates are enough to uniquely determine the state. Moreover, these corresponding product states are arranged into five orthonormal bases. We design five quantum circuits, which are decomposed into the common gates in universal quantum computation, to simulate the five projective measurements onto these bases. At the end of each circuit, we measure each qubit with the projective measurement {|0⟩⟨0|,|1⟩⟨1|}. Then, we consider the open problem whether three orthonormal bases are enough to distinguish all two-qubit pure states. A necessary condition is given. Suppose that there are three orthonormal bases 


A quantum state is the carrier of quantum information. One of the central topics in quantum science is the ability to characterize and manipulate quantum states, which would be applied to quantum communications, quantum cryptography, and quantum computation. Suppose that there is an unknown quantum state. It is impossible to create an identical copy of this state by the no-cloning theorem.[1] However, the information of the unknown quantum state can be transmitted to a remote location by the process of quantum teleportation,[2] with the help of classical communication and previously shared quantum entanglement. Now consider the following problem. There is a machine which can produce a large number of identical unknown quantum states. We are permitted to design any device to repeatedly measure this state and read out the probability distributions of the measurement outcomes. Can we infer all the information of the unknown state?
This is the problem of quantum state tomography. Two aspects are essential for this problem: the measurements and the method to reconstruct the unknown state via the measurement probabilities. Various measurements are considered for achieving quantum state tomography, such as Pauli measurements,[3,4] projective measurement onto mutually unbiased bases,[5–8] or onto general orthogonal bases,[9–12] and symmetric informationally complete measurements.[13–15] The data of measurement probabilities is collected after we take measurements on the ensemble of identical unknown quantum states. There are different methods applied on the data in order to calculate all the coefficients of the unknown state, such as linear inversion,[16,17] maximum-likelihood estimation,[9,18,19] Bayesian mean estimation,[20] and the convex optimization program.[12,21]
In this paper, we focus on the two-qubit pure state tomography. From the result of papers,[9,22] the density matrix of an unknown two-qubit state can be determined with the expectation values of 16 Pauli measurements. It was proved that a two-qubit pure state |ϕ⟩ is uniquely determined among all states (UDA) with 11 Pauli measurements.[4] That is to say, there does not exist any other state, pure or mixed, which has the same measurement results as |ϕ⟩. The projective measurements of five mutually unbiased bases have the same property.[6] In Ref. [12], another set of five orthonormal bases are constructed by a sequence of orthogonal polynomials. The method of the convex optimization program can be used to search for a density matrix, whose measurement probabilities match the data obtained experimentally. It has been found that several projections onto the tensor products of Pauli eigenstates are enough for two-qubit pure states tomography. These tensor product states are arranged into five orthonormal bases. Furthermore, the projective measurements onto these bases is simulated by five quantum circuits. Each circuit is decomposed by the common quantum gates used in universal quantum computing,[22] which is the footstone in building a universal quantum computer and has been researched on various materials. The measurement parts are the projective measurement {|0⟩⟨0|,|1⟩⟨1|} on each qubit. We can directly calculate the unknown two-qubit pure state with partial measurement probabilities of these bases.
Moreover, a necessary condition is given for the unsolved problem of whether three orthonormal bases can distinguish all two-qubit states. This problem dates back to the famous Pauli problem, whether or not the position and the momentum distributions can uniquely determine the wave function of a particle (up to a global phase).[23] The answer to the Pauli problem is negative and many related topics have been studied. The finite version of Pauli problem is considered by Asher Peres.[24] He noted that the probabilities of two orthonormal bases should be sufficient to determine a finite dimensional pure state up to a set of ambiguities. The findings in Ref. [25] suggest that the set is not a set of measure zero. A general question is the following. How many different orthonormal bases are needed at least in order to uniquely determine a pure quantum state in d-dimensional Hilbert space 
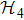





The rest of this paper is organized as follows. In Section
As a warm up, let us consider the one-qubit state tomography. It is known in many textbooks that three orthonormal bases uniquely determine an unknown qubit state,[22] which can be the eignenbases of Pauli operators σx, σy, and σz. Denote the eignenbases as {|+⟩, |−⟩}, {|L⟩, |R⟩}, and {|0⟩,|1⟩} correspondingly. Here


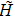
Let U be a d × d unitary operation. If we want to measure a d-dimensional pure state |ϕ⟩ with the projective measurements onto the orthonormal bases {U|0⟩,..., U|d − 1⟩}, we can take the unitary operation U† on the state |ϕ⟩, then measure U†|ϕ⟩ with the projective measurements onto the orthonormal bases {|0⟩,..., |d − 1⟩}. As the probabilities of the j-th outcome for both sides are equal, |⟨ψ|U|j⟩|2 = |⟨j|U†|ψ⟩|2, where j = 0,..., d − 1.
Let V1 and V2 be the unitary transition from basis {|0⟩, |1⟩} to basis {|+⟩, |−⟩} and {|L⟩, |R⟩}. Then V1 = H, 

Now, we construct five product orthonormal bases to directly determine an unknown two-qubit pure state, which are as follows:

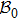
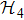

Next we use the circuits to simulate the projective measurements onto the bases 







An arbitrary unknown two-qubit pure state, separable or entangled, can be expressed with the vector form a|00⟩ + b|01⟩ + c|10⟩ + d|11⟩, where |a|2 + |b2| + |c|2 + |d|2 = 1. Any complex number g can be expressed as |g|eiθg. So we can write the unknown state with a new form

If we measure |ϕ⟩ with the projective measurement onto the basis 





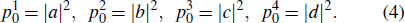
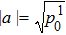
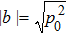


At least one probability in 


For example, the probabilities of the basis 




| Table 1. The nonzero probability and the corresponding state. . |
There are 




When 

When 

When 

When 

When 

There are four subcases in total. For example, 
When 

When 
When 
We write the unknown two-qubit pure state as |a||00⟩ + |b|eiθb|01⟩ + |c|eiθc|10⟩ + |d|eiθd|11⟩. We can use Eqs. (
Now we draw a conclusion. The coefficients {|a|, |b|, |c|, |d|} can be calculated by the probabilities 


Let 




Denote three orthonormal bases as 









Here we give the proof. Without loss of generality, the zero matrix element is x11. We may as well let the first rows of matrix U1 and U2 be real numbers. Namely, xk1 and yk1 are all real, k = 1, 2, 3, 4. This is because the probabilities that state |ϕ⟩ collapses to the basis states |ϕk⟩ or c|φk⟩ are equal, |c| = 1. So the bases {|ϕ1⟩, |φ2⟩, |ϕ3⟩, |ϕ4⟩}, and {c1|ϕ1⟩, c2|ϕ2⟩, c3|ϕ3⟩, c4|ϕ4⟩} have the same power of discrimination, where |ck| = 1 for k = 1, 2, 3, 4.
We can construct a pair of unnormalized vector states:



It is easy to prove that their probability distributions onto the first basis 

For the second basis 



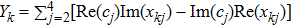

Define 


Now we consider the following linear equations:




Then,



The zero element may appear at the j-th row of the matrices U1 or U2. Then the two vector states can be constructed as: |Φ1⟩ = |j⟩ + ∑k ≠ j [Re(ck) + i· Im(ck)]|k⟩, |Φ2⟩ = |j⟩ − ∑k ≠ j[Re(ck) + i · Im(ck)]|k⟩. With a similar analysis, there exists a nontrivial solution so that the probability distributions onto the three orthonormal bases are equal. This completes the proof.
This necessary condition can give us some insights to the minimal number of orthonormal bases which can distinguish all two-qubit pure states. If the minimal number is actually three, we should find them with the constraint of the condition. For example, if we choose basis 

In this paper, we show that any unknown two-qubit pure state can be directly reconstructed by the measurement probabilities of projections onto 16 tensor products of Pauli eigenstates. These projections are arranged into five orthonormal bases. Moreover, we construct five quantum circuits to simulate the projective measurements onto the states of these bases. In the end, we focus on the unsolved problem of whether three orthonormal bases can distinguish all two-qubit pure states. A necessary condition is given. If the condition is not satisfied, three orthonormal bases are not sufficient to distinguish all two-qubit pure states.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] |




















