Project supported by the National Natural Science Foundation of China (Grant No. 61332003) and the Natural Science Foundation of Hunan Province, China (Grant No. 2015JJ3024).
Project supported by the National Natural Science Foundation of China (Grant No. 61332003) and the Natural Science Foundation of Hunan Province, China (Grant No. 2015JJ3024).
† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61332003) and the Natural Science Foundation of Hunan Province, China (Grant No. 2015JJ3024).
We investigate the dependence of the switching process on the perpendicular magnetic anisotropy (PMA) constant in perpendicular spin transfer torque magnetic tunnel junctions (P-MTJs) using micromagnetic simulations. It is found that the final stable states of the magnetization distribution of the free layer after switching can be divided into three different states based on different PMA constants: vortex, uniform, and steady. Different magnetic states can be attributed to a trade-off among demagnetization, exchange, and PMA energies. The generation of the vortex state is also related to the non-uniform stray field from the polarizer, and the final stable magnetization is sensitive to the PMA constant. The vortex and uniform states have different switching processes, and the switching time of the vortex state is longer than that of the uniform state due to hindrance by the vortex.
The STT-MRAM has attracted extensive attention from academia and industry as a novel nonvolatile memory technology since 1996.[1,2] Due to its fast programming speed, high storage density, and low energy consumption, STT-MRAM has become one of the strongest contenders among nonvolatile memory candidates.[3–6] Compared with the traditional in-plane STT-MRAM, perpendicular STT-MRAM,[7–10] with its unique theoretical advantages of lower switching current density and higher thermal stability, has become the mainstream type of STT-MRAM. It is common knowledge that switching current density is very sensitive to the spin configuration and dynamics of magnetic tunnel junctions (MTJs). However, with the further reduction in device dimension, the junction dimension is comparable to the exchange length of the system,[11] which makes spin configurations very susceptible to fabrication processes,[12–14] and the current density becomes less predictable. Therefore, stabilization and manipulation of the spin configurations become key problems that need to be solved urgently. To overcome these problems, the study of the underlying physics of the switching mechanisms of perpendicular MTJs (P-MTJ) is essential. It is well known that the perpendicular magnetic anisotropy (PMA)[7,15] constant, Ku, plays an important role in the switching process of P-MTJs. Many studies focus on the dependence of PMA on magnetic multilayer film structures, such as CoFeB/Pt and CoFeB/Ni,[16,17] but the detailed mechanism by which Ku affects the switching process is still not clear. Because most investigations of the switching process have been based on the macrospin model,[18,19] such a mechanism cannot be explained with a simple macrospin model. Only micromagnetic simulations can reveal the detailed spin dynamics during the switching process. Therefore, micromagnetic simulations are essential to obtain deep insights into the switching processes.
In this study, we systematically investigated the switching process dependence on Ku for typical P-MTJ structures with a wide range of Ku by employing the Object Oriented Micromagnetic Framework (OOMMF),[20] a public domain simulator, with the public STT extension module.[21] We calculated the average normalized out-of-plane magnetization Mz/Ms and found the final stable spin configurations of the free layer with various Ku. According to these results, the final stable state of the free layer can be divided into three different states: vortex, uniform, and steady. In addition, we analyzed the formation mechanism of the three different states, especially for the vortex state and its correlation with Ku. Finally, through showing the time evolution of the spin configurations, the effects of Ku on the vortex and uniform state switching processes are compared.
Figure
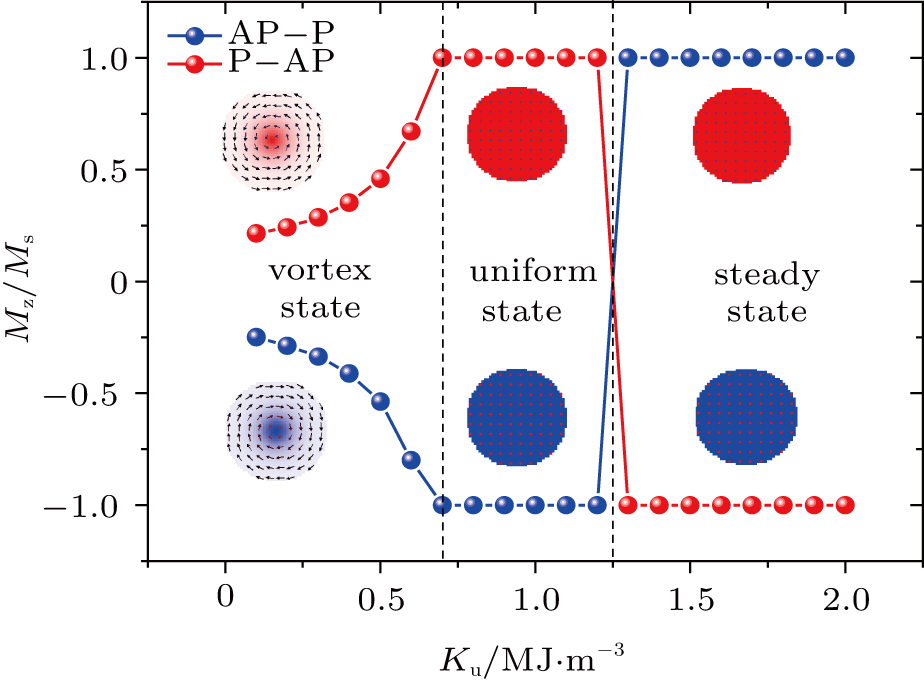
We calculated the average normalized out-of-plane magnetization, Mz/Ms, of the free layers of AP-parallel (P) and P-AP switching processes with various Ku. To implement the interface anisotropy, we varied Ku from 1.0 × 105 to 2.0 × 106 J/m3 because the surface PMA of the free layers were varied from 0.5 × 10−4 to 1.0 × 10−3 J/m2. Figure
Considering that the stable state of spin configuration is determined by the trade-off of inner energy,[23] the stable state of the free layer after switching for the initial P-state is the same as that after relaxation for the initial AP-state. Thus, we can explain the mechanism of vortex generation by analyzing the relaxation process for the corresponding initial state. Although there have been many previous studies on vortex states,[24–27] all of the research was focused on the in-plane magnetic anisotropy (IMA) materials. As a result, the detailed mechanism of vortex generation and the correlation with Ku for PMA materials still need to be elaborated.[28] Figure
When Ku > 0.7 × 106 J/m3, the maximum PMA energy is greater than the initial demagnetization energy; therefore, the final magnetization distribution after switching maintains a uniform state that is perpendicular to the horizontal plane. It is common knowledge that the intrinsic threshold current is proportional to Ku for the P-MTJ.[7] When the value of Ku increases to 1.3 × 106 J/m3, the current density Jc = 2.0 × 1011 A/m2 that was set in our simulation is not enough to overcome the anisotropy energy, and the magnetization of the free layer thus remains in the initial state.
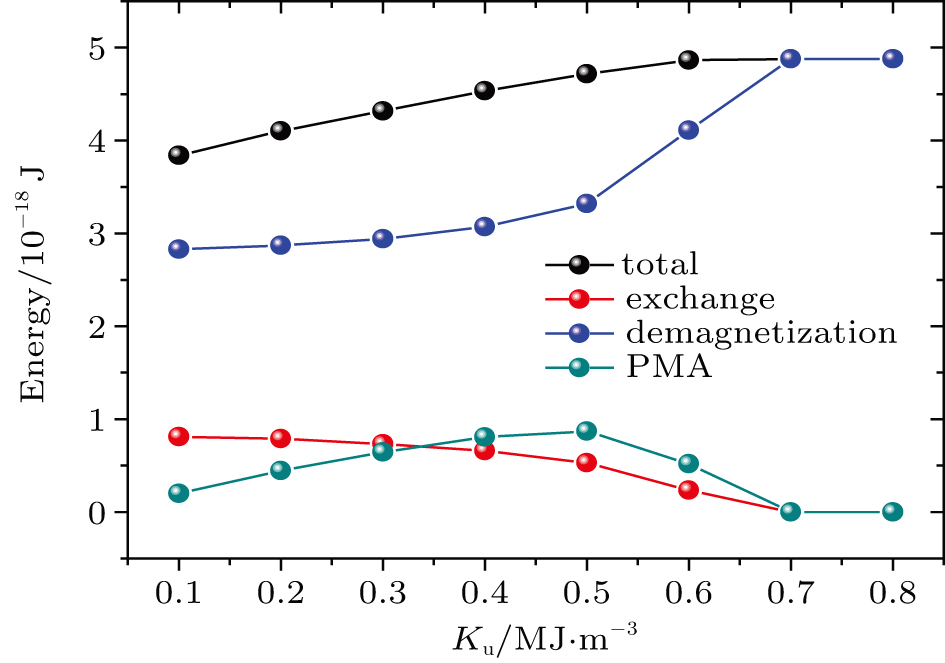
To analyze the dependence of the vortex state on Ku in depth, we plot the total, exchange, demagnetization, and PMA energies as functions of Ku for the free layer stable state after switching for initially AP-states in Fig. 
Finally, to show the switching process of different states more intuitively, we obtained snapshots of the spin configurations of the free layer for the AP–P switching process at Ku = 0.2 × 106 J/m3 and Ku = 0.7 × 106 J/m3, as shown in Figs.
 | Fig. 5. (color online) Time evolution of spin configurations of the free layer for AP–P switching process at Ku = 0.2 × 106 J/m3. (a) Nucleation, (b) periodic precession, and (c) damped oscillation. |
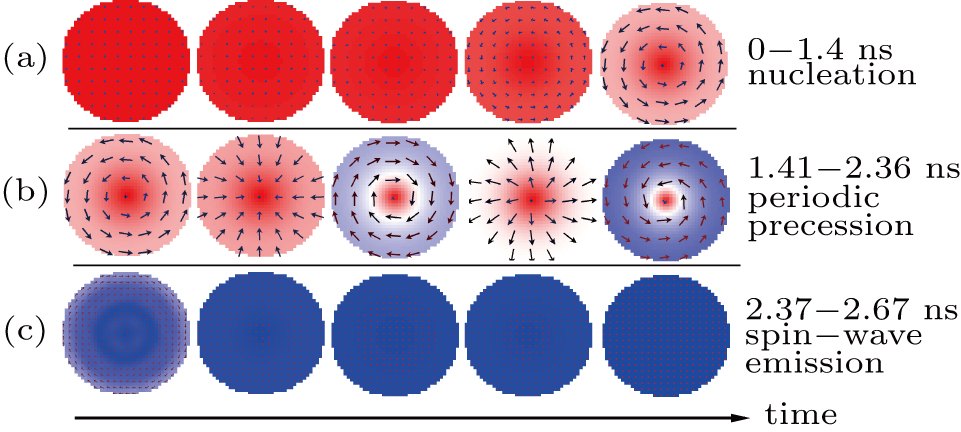 | Fig. 6. (color online) Time evolution of spin configurations of the free layer for AP–P switching process at Ku = 0.7 × 106 J/m3. (a) Nucleation, (b) periodic precession, and (c) spin-wave emission. |
 | Fig. 7. (color online) Time-dependent average normalized out-of-plane magnetizations Mz/Ms for the initially AP-states MTJ structure with various Ku (0.2, 0.7 MJ/m3). |
Figure
The final stable states of the spin configurations after current induced switching for P-MTJ are divided into three types as vortex, uniform and steady states based on the value of the PMA constant. The mechanism can be explained by the energy trade-off in the system. The generation of the vortex state is attributed to the non-uniform stray field from the polarizer, and the variations of the demagnetization, exchange, and PMA energies determine the final stable state. Besides, the average out-of-plane magnetization component of the vortex state is sensitive to the PMA constant. Finally, we demonstrate the time evolution of the spin configurations for the switching processes of the vortex and uniform states and find that the switching time of the vortex state is longer than that of the uniform state because of the hindering action of the vortices in the switching process. Therefore, avoiding the vortex state may be an effective way to improve the switching speed of the P-MTJ.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] |