Generally, magnetostriction is the deformation of materials influenced by an external magnetic field. The magnetostrictive effect was first presented by James Joule in 1842,^[1] and nowadays the magnetostrictive materials are widely used for micro/nano-level actuation. Due to the characteristics of fast response, high resolution, and high force capacity, magnetostrictive actuators are designed for various applications, such as high speed precision milling machines, hydraulic valves, and active damping systems.^[2–4] However, the input–output property of magnetostrictive actuators exhibits considerable hysteresis nonlinearities which deeply reduce their accuracy. Furthermore, their hysteresis curves tend to be asymmetric when driven by moderate or higher amplitude excitations.^[5–7]

To address this problem, a number of hysteresis models have been proposed to describe and compensate for the hysteresis of magnetostrictive actuators. The physics-based models are generally derived on the basis of a physical measure, such as magnetization, stress–strain, and energy principles.^[8–12] They are usually presented in a complex mathematic format and thus are difficult to invert. Therefore, many phenomenological models, such as Preisach^[13–16] and Prandtl–Ishlinskii (P–I) models,^[17–20] are proposed. They can be regarded as a superposition of hysteresis operators in relatively simple mathematic formats. Furthermore, P–I models are analytically invertible so that it is convenient to use them to compensate for the hysteresis of magnetostrictive actuators.^[18,21,22]

The classical Prandtl–Ishlinskii (CPI) model is composed of a series of classical operators and an input function. Generally, it can only efficiently describe the symmetric hysteresis nonlinearity. To overcome this limitation, much research focuses on the optimization of the classical operators. Therefore, various complex operators have been developed to replace the classical operator. Al Janaideh et al. proposed a generalized Prandtl–Ishlinskii (GPI) model established by a superposition of generalized hysteresis operators.^{[17, 22]} These generalized operators are formulated by the relatively complex envelope functions, and thus the GPI model can describe the asymmetric and saturated hysteresis properties of different smart actuators. Guanqiao Shan et al. studied the hysteresis properties of the voice coil motor experimentally and introduced a modified GPI model to compensate for its asymmetric hysteresis.^[23] Kuhnen combined a conventional P–I operator and a dead-zone operator which is used to describe memory-free nonlinearities, and established a new P–I model to describe and compensate for the asymmetric hysteresis of magnetostrictive actuators.^[24] These models can describe the asymmetric hysteresis exhibited by magnetostrictive actuators. However, limitations exist in the complex operators when inverting these models mathematically. To balance the modeling performance and model complexity, Guoying Gu et al. focused on the optimization of the input function and introduced a modified Prandtl–Ishlinskii (MPI) model by replacing the linear input function with polynomial functions.^{[18, 21]} The MPI model only changes the input function and maintains the CPI operator. Therefore, it has a relatively simple mathematic format. More recently, Jinqiang Gan et al. added a quadratic polynomial on the basis of the CPI model.^[25] This model could describe both rate-independent and rate-dependent hystereses in piezoelectric actuators. Micky Rakotondrabe proposed a multivariable hysteresis model based on the extension of the CPI (monovariable) model.^[26] This model avoided the model inversion and could compensate for the hysteresis nonlinearity in a two-degrees-of-freedom (2-DOF) piezoactuator. However, these models have only been verified on piezoceramic actuators and their description of magnetostrictive actuators has not been explored. As illustrated in Ref. [27], all algorithms perform equally on all modeling problems. Therefore, there are still problems that can be solved better by new algorithms. This is the main motivation of this work, in which a new P–I model along with its parameter identification method is proposed for magnetostrictive actuator modeling specifically.

To describe the asymmetric hysteresis phenomenon of magnetostrictive actuators more efficiently, it is necessary to modify the input function for the CPI model. In this paper, a modified rate-independent Prandtl–Ishlinskii (MRIPI) model is introduced for the asymmetric hysteresis description of magnetostrictive actuators. The MRIPI model maintains the classical operator of the CPI model and replaces the linear input function with the Fermi–Dirac distribution. This model has fewer parameters to be identified. Since the MRIPI model only changes the classical input function, it has a relatively simple mathematic format. Compared with the models mentioned above, it is more efficient to establish the MRIPI model and describe the hysteresis phenomenon of magnetostrictive actuators. The properties of this proposed model are characterized. Then the validity of the resulting MRIPI model is demonstrated by comparing the model responses with the measured asymmetric hysteresis of magnetostrictive actuators. Additionally, the performances of the CPI, MPI, GPI, and MRIPI models are compared to analyze the performance of the MRIPI model in describing the asymmetric hysteresis of magnetostrictive actuators. It should be clarified that this study only focuses on the hysteresis independent of the input rate which is called rate-independent hysteresis.

Since the proposed MRIPI model is on the basis of the CPI model, before introducing the MRIPI model, the CPI model is reviewed in brief.

2.1. CPI model

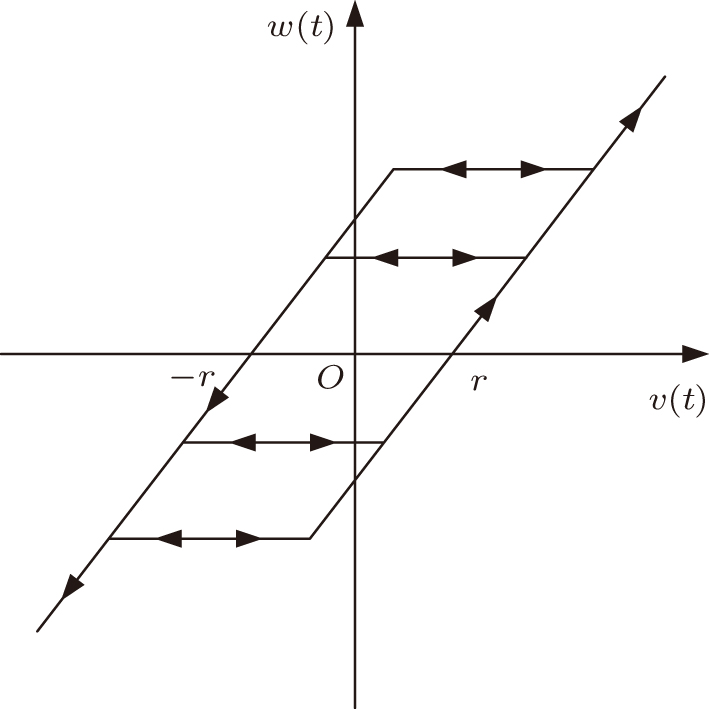
The CPI model^[15] is a widely accepted phenomenological model. The model is composed of a series of weighted operators and a linear input function. The play operator F_r[v](t), as shown in Fig. 1, is defined by the input v(t) and the threshold r. Assume that C_m[0,T] is the space of the piecewise monotone continuous functions. For any input v(t)∈C_m[0,T], where 0=t₀ < t₁ < ⋯ < t_n = T are intervals in [0,T], the output of the play operator w(t) can be described by

for t_i < t ≤ t_{i + 1}, 0 < i ≤ n − 1, withThe initial value w(0) of the play operator F_r[v](0) can be described byIt has been verified that for any monotone input, the play operator is Lipschitz continuous and monotone.^[15] More detailed discussions about this operator are presented in Refs. [15] and [22].

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Input–output relationships of the classical play operator.

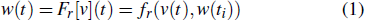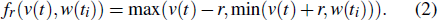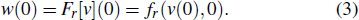The CPI model utilizes a series of weighted operators F_r[v](t) mentioned above to describe the relationship between the input v(t) and the output w(t). The formula of the CPI model φ_c(t) can be defined by

where p₀ is a positive constant, and p(r) is a positive density function. p₀ and p(r) are generally calculated according to the experimental data. As illustrated in Fig. 2, the CPI model can only describe the symmetric hysteresis nonlinearity efficiently. However, the real hysteresis nonlinearity of magnetostrictive actuators exhibits the asymmetric property, especially when they are driven by moderate or higher amplitude excitations. Therefore, this study proposes an efficient and relatively simple model that can describe the asymmetric hysteresis of magnetostrictive actuators accurately.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Hysteresis loops generated by the CPI model with p0 = 1.25, p(r) = 0.07e−0.1r, r ∈ [0,1], and the input v(t) = 5sin(2πt) + 4cos(6t).

2.2. MRIPI model

Considering that the CPI model is devoted to the description of the symmetric hysteresis, a novel MRIPI model based on the Fermi–Dirac distribution is proposed in this study to characterize the asymmetric hysteresis behavior of magnetostrictive actuators. The CPI model is composed of two parts mathematically, a series of weighted operators and a linear input function. The previous proposed models, as mentioned in Section 1, mostly focus on complicating the weighted operators to breakthrough the limitation of the CPI model.^{[17, 22, 24]} Little research has been conducted on the linear input function. Although Gu et al. introduced a MPI model by modifying the linear input function,^{[18, 21]} the generalized input function proposed by them has only been verified on piezoceramic actuators. In this study, a simplified Fermi–Dirac distribution is introduced to replace the classical linear input function and the classical operator is maintained. With this method, the MRIPI model can describe the asymmetric hysteresis of magnetostrictive actuators accurately in a relatively simple mathematic format with fewer parameters to be identified.

The hysteresis of magnetostrictive actuators is mainly caused by the magnetization hysteresis of the magnetostrictive materials. It is suggested that the magnetic domains can be described by fermions.^[11] Therefore, the Fermi–Dirac distribution can be applied to the magnetic domains. The Fermi–Dirac distribution is usually defined as

where f(E) is the probability of a particle having energy E, E_F is the Fermi energy, k is the Boltzmann constant, and T is the absolute temperature. By defining p = 1/(kT) and q = −E_F/(kT), equation (5) can be rewritten asSince the Fermi–Dirac distribution can characterize the properties of the magnetic domains, it is expected to be efficient in magnetization hysteresis description. The proposed MRIPI model replaces the classical linear input function with an extended Fermi–Dirac distribution g[v](t) as follows:where s is a constant to extend the range of Eq. (6). Therefore, the proposed MRIPI model φ_o(t) is formulated as

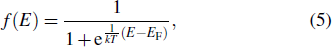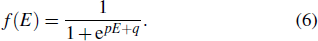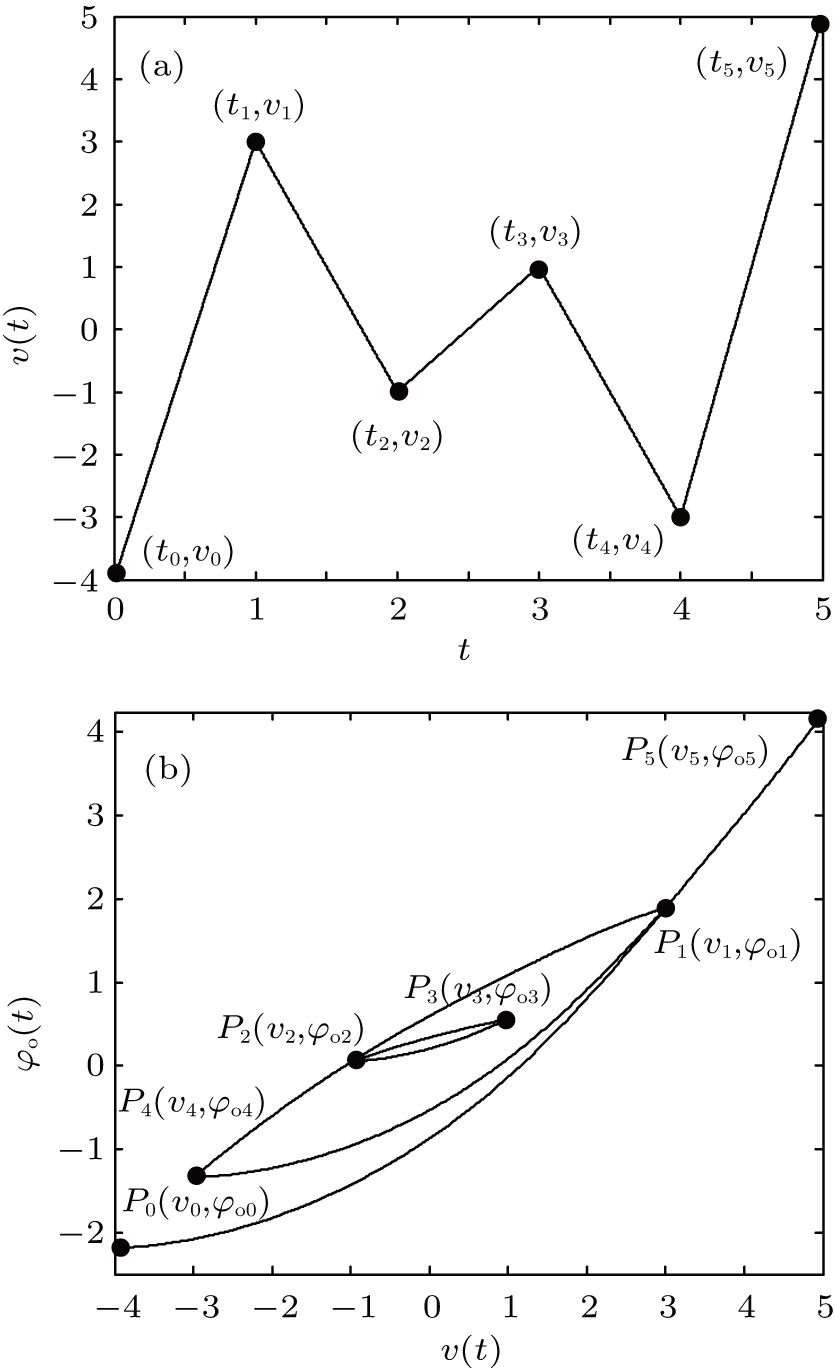
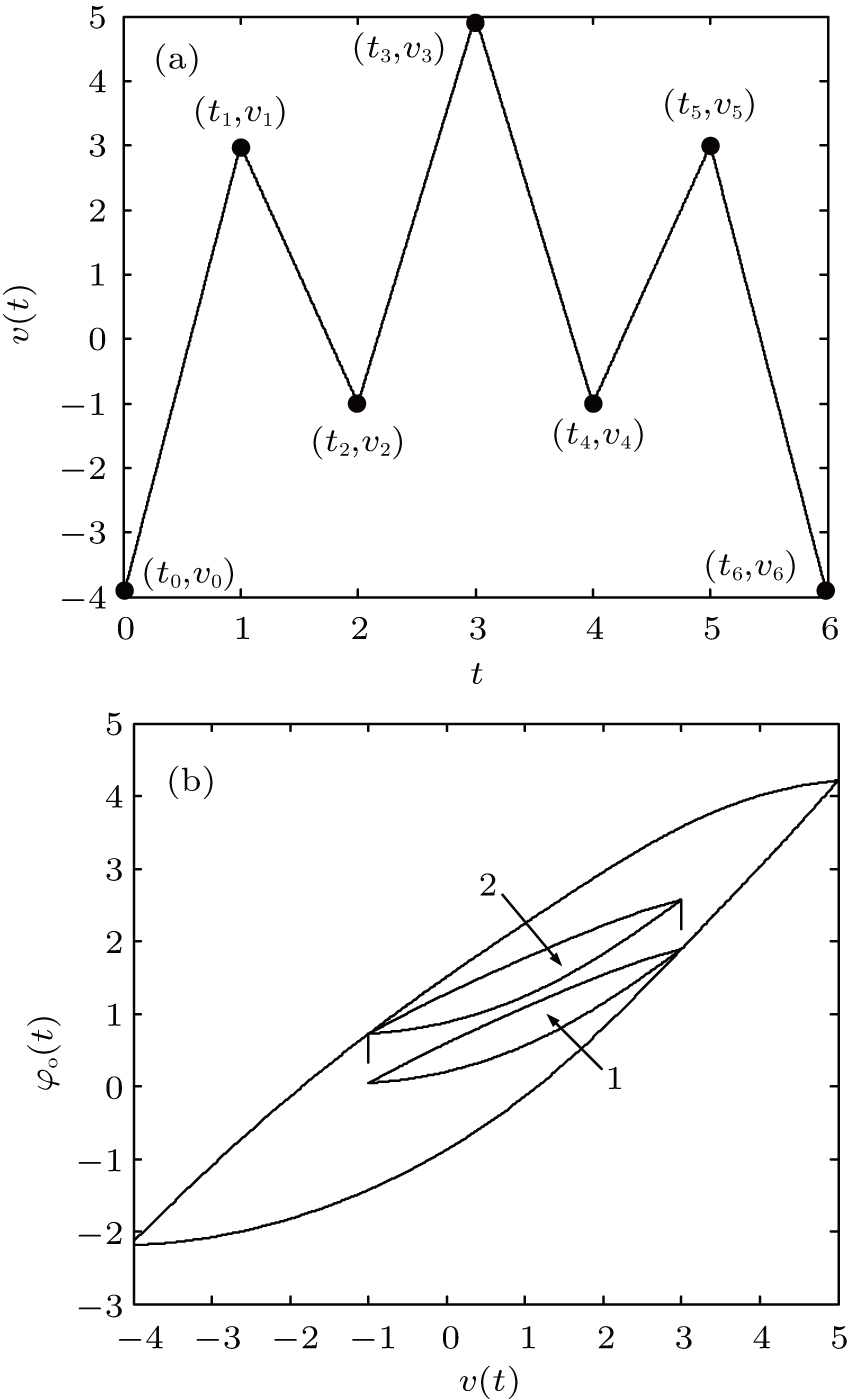
The wiping-out and congruency properties are two basic properties of the operator-based hysteresis models and thus they are essential for the validity of the P–I models.^{[13, 28]} According to the Lagrange mean value theorem, the Fermi–Dirac distribution is Lipschitz continuous. Therefore, the proposed MRIPI model fulfills these two properties in theory. The simulations are performed to verified these two properties of the MRIPI model as follows.

3.1. Wiping-out property

The wiping-out property refers to the behavior that any local extremum of the input value wipes out the memory stored by the previous local extrema whose absolute value is smaller than that of the present local extremum.^{[13–15, 28]} To exhibit the wiping-out property, a special string sequence v(t) is given as the input of the MRIPI model, as shown in Fig. 3(a). This input string sequence contains six extrema denoted by v₀, v₁, v₂, v₃, v₄, and v₅. Figure 3(b) illustrates the output of the MRIPI model with the input string sequence mentioned above. The density function and the input function of the MRIPI model are p(r) = 0.07e^−0.1r and g[v](t) = 1/(1 + e^{−v + 2.4}), respectively. Initially, the input v(t) increases from v₀ to its first maximum v₁, as shown in Fig. 3(a). Accordingly, the output of the MRIPI model φ_o(t) increases from φ_o0 to φ_o1 via the curve P₀P₁. Then the input v(t) decreases from v₁ to its first minimum value v₂ and the corresponding output φ_o(t) decreases from φ_o1 to φ_o2 via the curve P₁P₂. Subsequently, the input v(t) increases from v₂ to its second maximum v₃. Accordingly, the output φ_o(t) increases from φ_o2 to φ_o3 via the lower curve between P₂ and P₃. Since φ_o3 < φ_o1, the wiping-out phenomenon does not occur so far. Afterwards, the input v(t) decreases from v₃ to its second minimum value v₄. Since φ_o4 < φ_o3, the output φ_o(t) deorbits from the P₂P₃ loop branch and decreases from φ_o3 to φ_o4 via the curve P₃P₂P₄. In this situation, the memory of P₂(v₂, φ_o2) is wiped out by the memory of P₄(v₄, φ_o4). Finally, the input v(t) increases from v₄ to its third maximum v₅. Since φ_o5 > φ_o4, the output φ_o(t) deorbits from the P₁P₂P₄ loop branch and increases from φ_o4 to φ_o5 via the curve P₄P₁P₅. Thus the memory of P₁(v₁,φ_o1) is wiped out by the memory of P₅(v₅,φ_o5). This simulation shows that the local maximum (minimum) input value will wipe out the memory stored by the previous smaller (larger) local maximum (minimum). Therefore, the wiping-out property of the proposed MRIPI model is verified.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Simulation of the wiping-out property of the proposed MRIPI model: (a) input current and (b) output hysteresis loops.

3.2. Congruency property

The congruency property refers to that the minor hysteresis loops generated by the same extrema of input are congruent.^{[13–15, 28]} To exhibit the congruency property, another special string sequence is given as the input of the MRIPI model, as shown in Fig. 4(a). This input string sequence contains seven extrema denoted by v₀, v₁, v₂, v₃, v₄, v₅, and v₆. On this occasion, assume that v₀ is equal to v₆, v₁ is equal to v₅, and v₂ is equal to v₄. Therefore, the input ranges [v₂,v₁] and [v₄,v₅] are the same. Figure 4(b) illustrates the output of the MRIPI model when the input is the string sequence mentioned above. The density function and the input function of the MRIPI model are the same as those introduced in Subsection Subsection 3.1. In Fig. 4(b), the minor hysteresis loop 1 corresponds to the output of the input ranges [v₂,v₁] via first a decreasing then increasing process, and the minor hysteresis loop 2 corresponds to the output of the input ranges [v₄,v₅] via first an increasing then decreasing process. It can be observed that these two minor hysteresis loops are completely congruent. Therefore, the congruency property of the proposed MRIPI model is verified.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Simulation of the congruency property of the proposed MRIPI model: (a) input current and (b) output hysteresis loops.

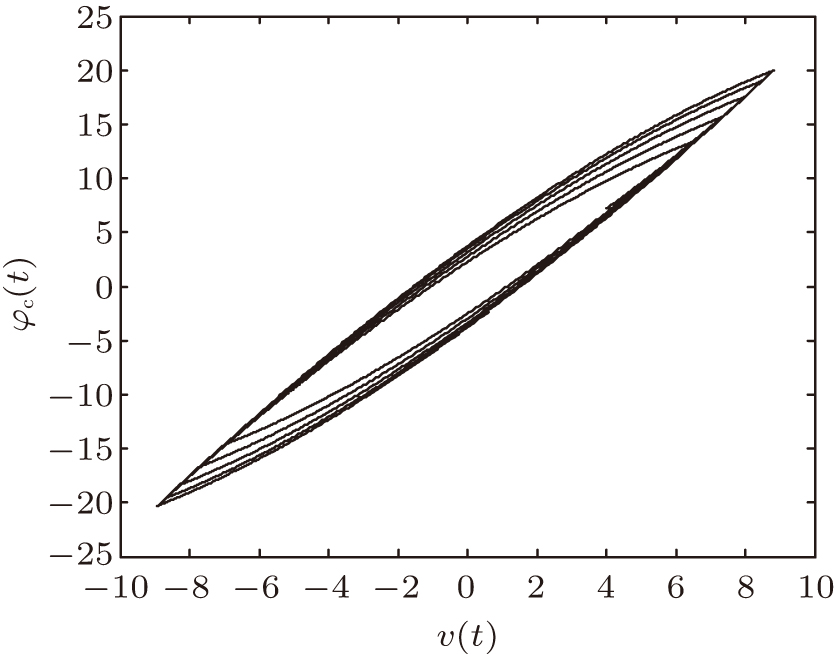
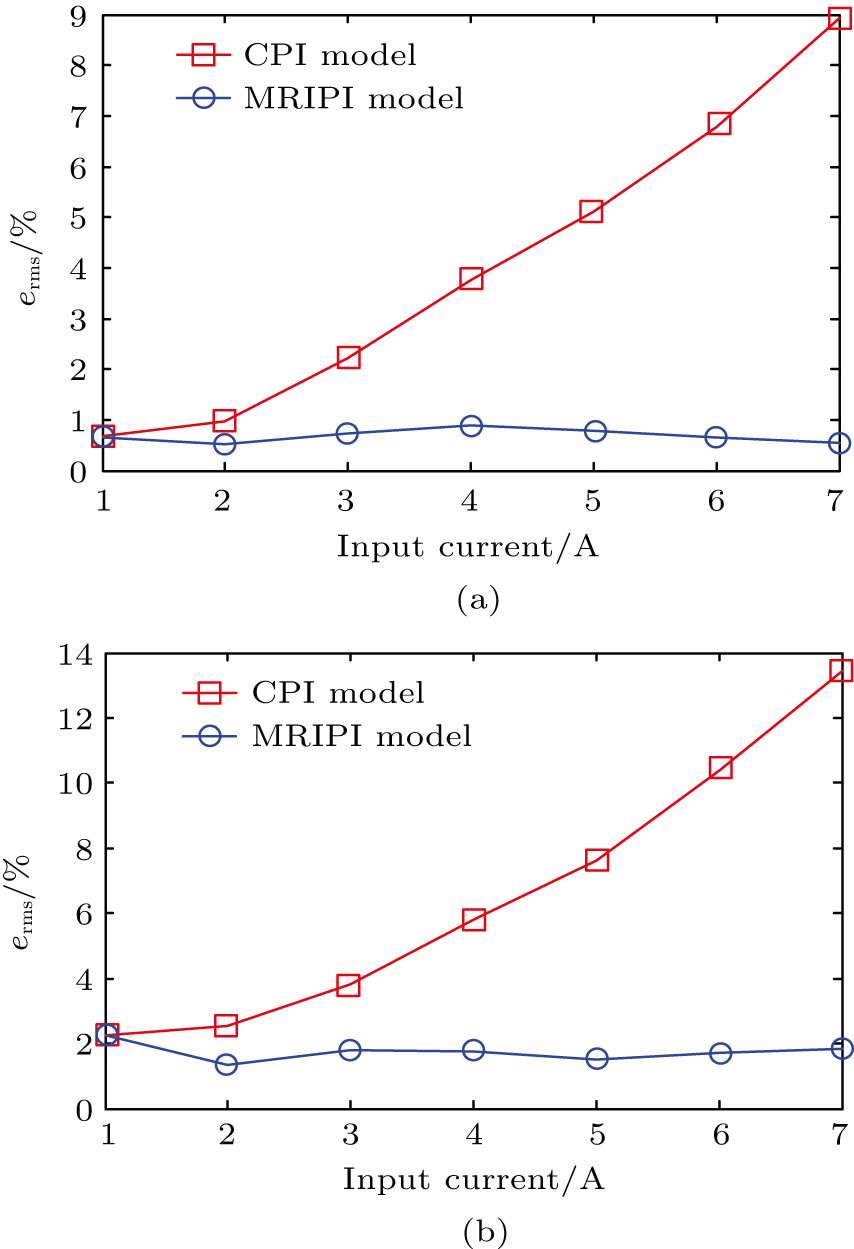
To verify the proposed MRIPI model, the model responses under different amplitudes of excitations are compared with the experimental data in this section. The experimental data of the magnetostrictive actuator analyzed in this paper is reported in Ref. [6] by Subhash Rakheja’s group. The input signals are the sinusoidal currents with amplitudes from 1 A to 7 A and a frequency of 10 Hz, and the output displacement exhibits different degrees of asymmetric hysteresis phenomena, as shown in Fig. 5. As reported in Ref. [6], the displacement of the magnetostrictive actuator is nearly symmetric when the amplitude of the input current is lower than 2 A, and the asymmetric phenomena become evident when the amplitude of the input current exceeds 2 A. More detailed information can be found in Ref. [6]. Additionally, the performances of the CPI, MPI, and GPI models are presented and compared with that of the proposed MRIPI model.

Fig. 5.

	Figure Option ViewDownloadNew Window
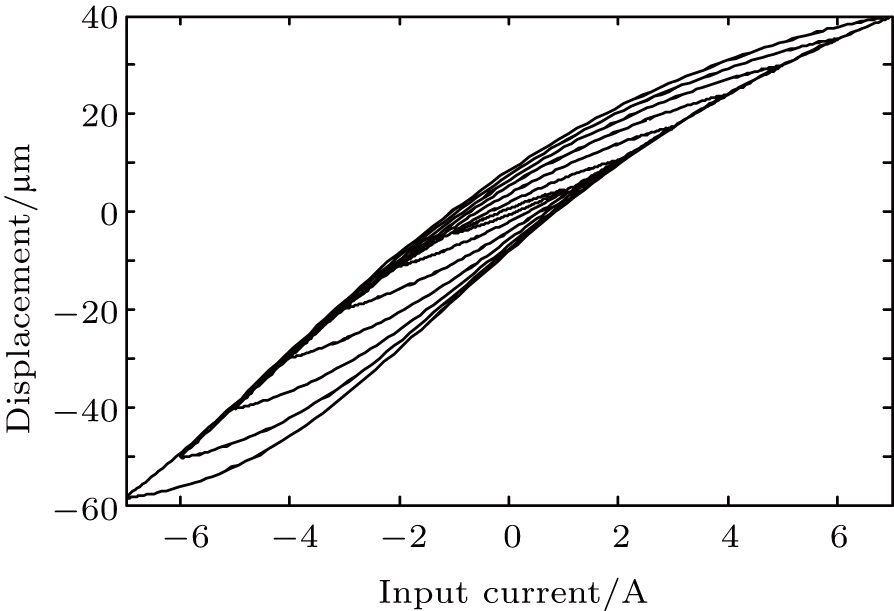	Fig. 5. The experimental data of the magnetostrictive actuator reported in Ref. [6]. The input signals are the sinusoidal currents with amplitudes from 1 A to 7 A and a frequency of 10 Hz.

In this study, the density function is defined by

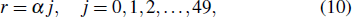To experimentally identify the parameters of the MRIPI model, a velocity-based sine cosine algorithm (VSCA) is proposed on the basis of the sine cosine algorithm (SCA).^[29] The population-based optimization usually consists of two phases: exploration and exploitation.^[30] In the exploration phase, the strategy focuses on widely searching to discover unknown information. However, in the exploitation phase, the strategy aims at finding the optimal solution around a good solution. These two phases must be carefully balanced to avoid slow convergence or local optima stagnation. In the traditional SCA, the position is updated by the following equation:

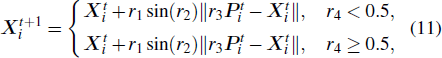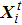
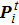
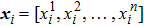
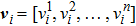
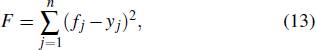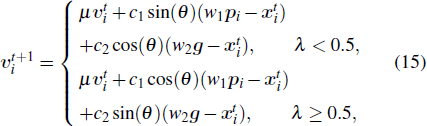In this study, the VSCA is proposed to improve the exploitation ability of the traditional SCA. In the VSCA, a swarm is composed of m particles. Each particle i is characterized by two vectors: the position vector and the velocity vector , where n refers to the dimension of the searching space. All the particles are evaluated by the fitness function F as follows:

To solve the problems of the SCA mentioned above, the VSCA introduces two variables: velocity v and global best value g. The velocity records the change tendency of the distance between the destination and the current position. If the current position is far away from the destination, the velocity will accumulate due to the acceleration during the updating steps. Also the friction factor μ is introduced to avoid overshooting when the particle is already very close to the destination. Therefore, compared with directly updating the position, indirectly updating the position via velocity can improve the searching speed efficiently. To avoid local optima stagnation, the VSCA associates the velocity with the global optimum. Thus, the new position of each particle refers to both the local optima and the global optimum. In this case, when a particle is trapped in a local optimum whose position is far away from that of the global optimum, it will probably jump out of the local optimum, move towards the global optimum, and search along the way again. In the VSCA, there are three states according to the updating equation: accelerating towards the destination, decelerating towards the destination, and decelerating outwards from the destination. When θ ∈ [0,π/2], the particle accelerates towards the destination rapidly. When θ ∈ (π/2,π] and λ < 0.5, the particle decelerates towards the destination, where it is either exploiting around the destination or preparing to jump out of the local optima. When θ ∈ (π/2,π] and λ ≥ 0.5, the particle decelerates outwards from the destination, where it is exploring other space out of the current optima space. Thus, the VSCA maintains the exploration ability of the SCA and improves its exploitation ability. Table 1 shows the performances of the VSCA and the SCA. The maximum number of iterations T is 200. The number of particles m is 50, 100, 150, and 200, respectively. The global optimum is around 37 and the local optima are higher than 38. It can be seen that when the number of particles is 50 the VSCA traps in the local optima four times out of ten while the SCA traps six times. As the number of particles increases, the performances of both algorithms are improved. However, the performance of the VSCA is still better than that of the SCA. It should be noted that the VCSA finds the global optimum every time when the number of particles is 200 while the SCA traps in the local optima three times. Therefore, the VSCA is used to identify the MRIPI and other P–I models.

Table 1.

Table 1.

Table 1. Performances of the VSCA and the SCA (T = 200). Unit: μm2 . ith m = 50 m = 100 m = 150 m = 200 VSCA SCA VSCA SCA VSCA SCA VSCA SCA 1 36.77 48.12 47.49 47.80 37.94 36.95 36.77 47.15 2 47.78 47.76 36.89 39.21 37.79 46.77 36.76 36.82 3 36.74 36.79 36.76 36.77 36.78 47.78 36.78 40.89 4 40.97 47.75 36.95 46.17 47.45 47.44 36.76 36.80 5 47.72 42.80 47.79 36.81 47.78 36.77 36.84 36.79 6 37.06 37.12 48.22 38.04 36.78 36.78 36.80 36.79 7 36.78 41.99 36.82 36.78 36.78 42.57 36.77 37.12 8 44.79 47.78 36.78 44.43 36.76 36.71 36.78 41.57 9 36.78 36.77 38.07 47.71 36.77 39.42 36.74 36.78 10 36.72 36.79 36.78 36.78 36.77 36.76 36.77 36.75 Average 40.21 42.37 40.25 41.15 39.16 40.79 36.78 38.75 Standard deviation 4.77 5.18 5.25 4.99 4.48 4.87 0.03 3.48

Table 1. Performances of the VSCA and the SCA (T = 200). Unit: μm2 .

Figure 6 illustrates the performances of the CPI model and the MRIPI model when the amplitudes of the input current are 1 A, 3 A, 5 A, and 7 A. In Fig. 6(a), it can be observed that the outputs of the CPI model match with the experimental data quite well when the amplitude of the input current is 1 A. However, it generates relatively large deviations, especially at both ends of the hysteresis loop, when the amplitudes of the input current exceed 3 A. Figure 6(b) shows the performance of the proposed MRIPI model under different amplitudes of excitations. It can be observed that the model matches with all the experimental data quite well. To quantify the performances of these models, the relative root-mean-square error e_rms is calculated by

Fig. 6.

	Figure Option ViewDownloadNew Window
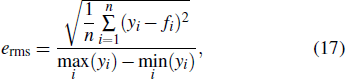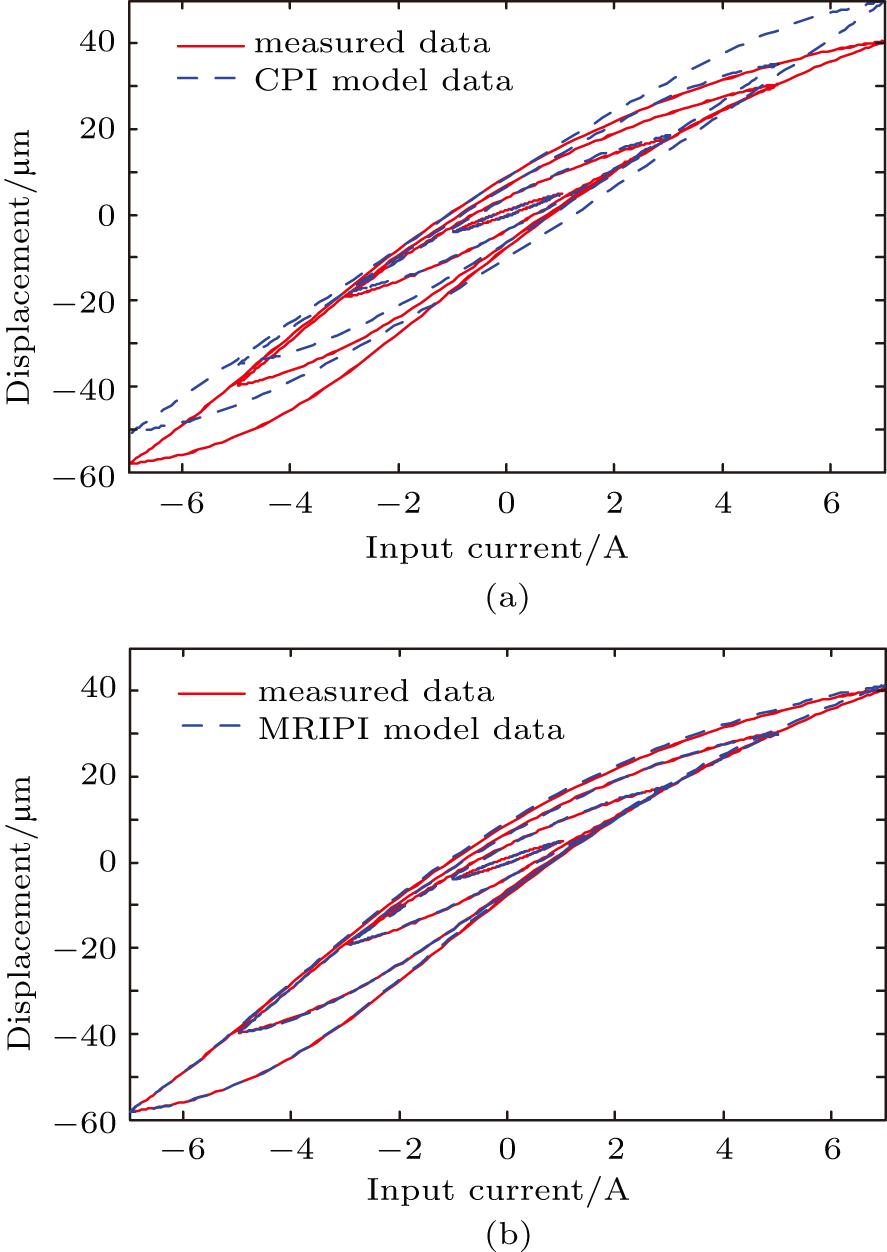	Fig. 6. (color online) Performances of (a) CPI model and (b) MRIPI model when the amplitudes of the input current are 1 A, 3 A, 5 A, and 7 A.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. (color online) Comparison of prediction errors, (a) the relative root-mean-square error erms and (b) the relative maximum error emax, between the MRIPI model and the CPI model as the amplitudes of the input current increase from 1 A to 7 A.

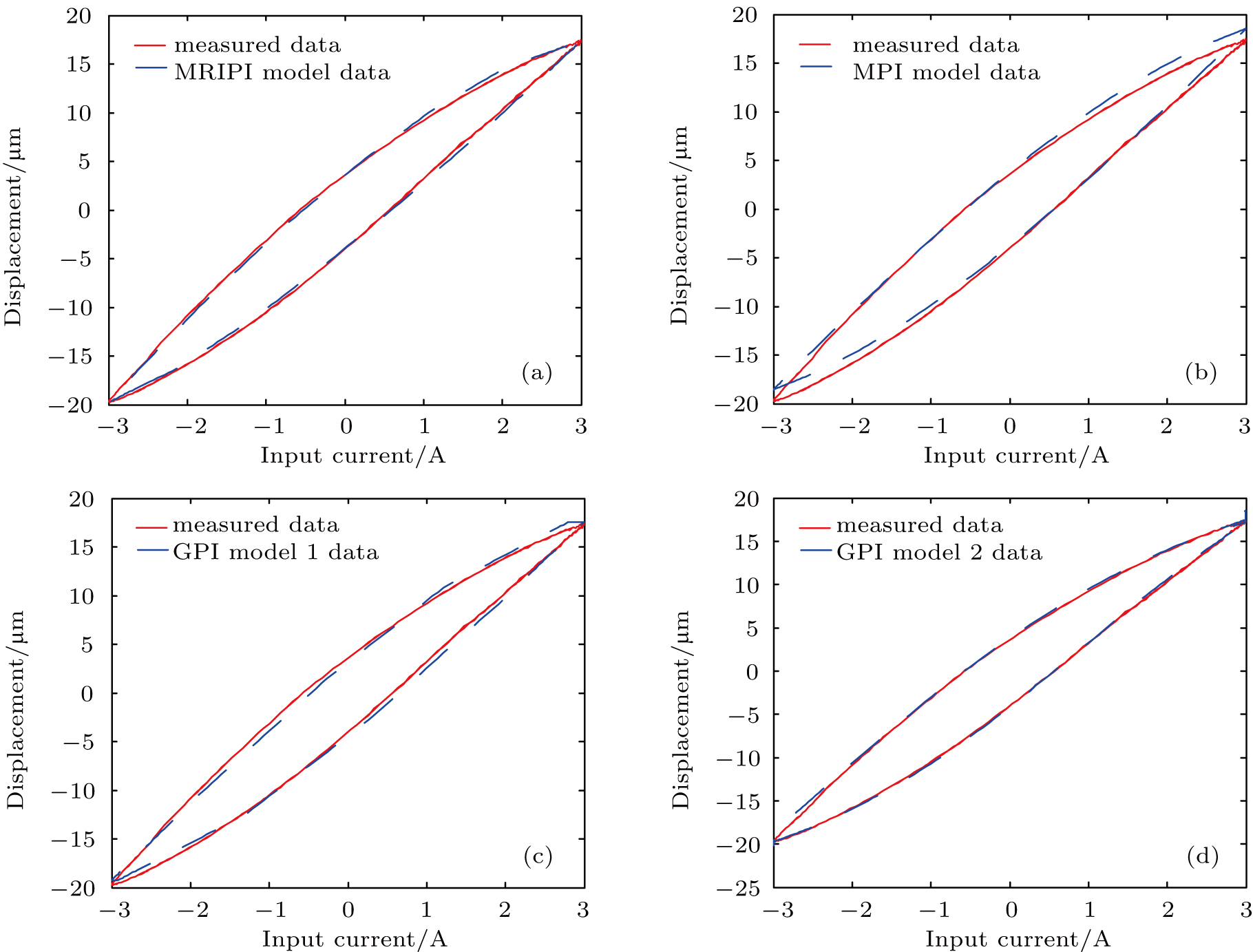
To further analyze the performance of the MRIPI model, the outputs of the MPI model and the GPI model are presented and compared with those of the MRIPI model. The input signal is the sinusoidal current with an amplitude of 3 A and a frequency of 10 Hz. In Fig. 8(a), it can be observed that the output of the MRIPI model matches with the experimental data quite well. Figure 8(b) shows that although the MPI model can describe the asymmetric hysteresis behavior of piezoceramic actuators, it is difficult to describe the asymmetric hysteresis behavior of magnetostrictive actuators. The possible reason is that the asymmetric hysteresis loop of magnetostrictive actuators exhibits evident saturation on both ends. The GPI model is proposed to describe the asymmetric hysteresis behavior of smart actuators, including magnetostrictive actuators. The outputs of the GPI models with different envelope functions are illustrated in Figs. 8(c) and 8(d), respectively. The GPI model 1 has linear envelope functions as mentioned at the beginning of this section. This model can describe the asymmetric hysteresis behavior without saturation. Since it is reported that the output saturation becomes evident when the input current exceeds 2 A,^[6] the performance of the GPI model 1 is limited in describing the asymmetric hysteresis behavior of magnetostrictive actuators driven by moderate or higher amplitude excitations. Therefore, the GPI model 2 with hyperbolic tangent envelope functions mentioned at the beginning of this section is proposed. It is observed that the output of this model matches the experimental data very well. However, compared with the proposed MRIPI model, this model has a relatively complex mathematic format with more parameters to identify.

Fig. 8.

Figure Option ViewDownloadNew Window

Fig. 8. (color online) Experimental verification of the MRIPI model with a sinusoidal input current and comparisons between the MRIPI model and other common P–I models: (a) MRIPI model data, (b) MPI model data, (c) data of the GPI model 1 with linear envelope functions, and (d) data of the GPI model 2 with hyperbolic tangent envelope functions. The amplitude of the input current is 3 A and the frequency is 10 Hz.

Table 2 lists the parameter number to be identified, the relative root-mean-square error e_rms, and the relative maximum error e_max of these four P–I models. The detailed parameter values are listed in Table 3. It can be seen that to achieve low errors there are fewer parameters to be identified for the MRIPI model, and thus the efficiency of the modeling process is improved. Although the parameter number of the MPI model is one less than that of the MRIPI model, the performance of the MRIPI model is much better than that of the MPI model. The smaller e_rms and e_max of the MRIPI model indicate that the proposed model has a better description of both the global and local characteristics of the asymmetric hysteresis behavior exhibited by magnetostrictive actuators. In conclusion, the proposed MRIPI model can well describe the asymmetric hysteresis behavior of magnetostrictive actuators in a relatively simple mathematic format.

Table 2.

Table 2.

Table 2. Performances of the P–I models. . MRIPI model MPI model GPI model 1 GPI model 2 Parameters 6 5 7 11 erms/% 0.71 2.18 1.19 0.70 emax/% 1.77 3.70 2.33 3.38

Table 2. Performances of the P–I models. .

Table 3.

Table 3.

Table 3. Parameters of the P–I models. . Parameter MRIPI model MPI model GPI model 1 GPI model 2 α 0.47 0.06 3.83 6.95 ρ 2.81 2.21 0.87 1.72 τ 0.95 0.32 0.18 0.09 s –4.8976 – – – p 1.05 0.02 – – q 3.19 2.40 – – a1 – – 4.78 12.27 b1 – – −0.69 0.33 c1 – – – –0.02 d1 – – – –0.43 a2 – – 4.88 16.41 b2 – – −0.03 0.24 c2 – – – 0.27 d2 – – – –3.19

Table 3. Parameters of the P–I models. .

The proposed modified classical Prandtl–Ishlinskii model identified by the VSCA can accurately characterize the asymmetric hysteresis behavior of magnetostrictive actuators. The performance of the MRIPI model is stable under different amplitudes of applied current. The relative root-mean-square error stays less than 1% and the relative maximum error stays less than 2% when the amplitudes of the input current increase from 1 A to 7 A. Compared with the classical Prandtl–Ishlinskii model, the proposed model has a better description of both the local and global asymmetric hysteresis behaviors exhibited by magnetostrictive actuators. Additionally, the proposed model has a relatively simple mathematic format with fewer parameters to be identified. Thus, it is more efficient to establish the MRIPI model and describe the asymmetric hysteresis phenomenon of magnetostrictive actuators. The performances of different Prandtl–Ishlinskii models are also compared to show better accuracies of the proposed model. The inverse model of the MRIPI model will be studied and the compensator control method of magnetostrictive actuators will be designed in the future.