Silicon carbide (SiC) has received remarkable attention as the representative of the third generation of semiconductor material for fabrication of high-power, high-frequency, and high-temperature devices, due to its physical and electronic properties, such as high breakdown electric field strength, high saturation electron velocity, and high thermal conductivity.^[1,2] SiC Schottky contact is the basic structure in SiC devices. The thermal annealing treatments after the deposition of metal into SiC are introduced to obtain highly reproducible SiC Schottky contacts^[3] and terminate the dangling bonds of SiC at the interface of metal/SiC to reduce the surface states of the structure.^[4] The reaction between the metal and SiC may occur at the interface during the annealing treatments, and the interface material, particularly the new phases formed in the interface, plays a key role in the electrical properties of the contact. The performance of SiC Schottky diode largely depends on the quality of the metal/SiC contact, and a reliable Schottky contact is necessary for high-power applications.^[5]

Barrier height (BH) and ideality factor (n) are the fundamental parameters of Schottky barrier diodes (SBDs). The reliable Schottky contacts of rectifiers require BH to be typically above ∼ 0.6 eV as well as low density of interface defects.^[6,7] The BH is likely to be a function of the interface atomic structure, and the atomic inhomogeneities at the metal-semiconductor (MS) interface which are caused by grain boundaries, multiple phases, facets, defects, a mixture of different phases, etc.^[8–11] In addition, Song et al.^[11] suggested that the barrier inhomogeneities could occur as a result of imperfect MS interface and lead to an abnormal variation of Schottky barrier height and ideality factor with varied testing temperature. Tung’s model^[8] assumed that nanometer-size patches with lower barrier height were embedded in a uniform high barrier background. The background with high barrier would pinch off the low-BH patch and the height of the saddle point would determine the current through Schottky contacts.

For the Schottky contact metal for high-temperature application, Maset et al. reported^[12] that the Ti and Ni metal layers typically used for commercial SiC Schottky diodes were not suitable for high-temperature operation, while tungsten showed superior chemical stability and reliability over a wide range of temperature, making it a perfect candidate for high-temperature and high-voltage applications.^[13–16] Ferhat et al. reported^[17] that the 500 °C annealed W/4H-SiC Schottky contact exhibited barrier inhomogeneities. Some researchers have studied the reaction between W and SiC at high temperatures,^[18,19] but the effects of annealing temperature on the properties of W/SiC Schottky contact, especially the degree of inhomogeneity of the BH, to the best of our knowledge, have not been investigated yet.

In the present work, we measure the electrical characterization of W/4H-SiC Schottky contacts formed at different annealing temperatures. The temperature dependence of ideality factor and BH indicates the formation of an inhomogeneous barrier, which can be conveniently interpreted by considering lateral non-homogeneous distributions of BH according to Tung’s model. The degree of inhomogeneity of the BH analyzed by the “T₀ anomaly” of Tung’s model is correlated to the temperature of thermal annealing treatment. Furthermore, the solid state reaction of W with 4H-SiC, the phase composition at different annealing temperatures, and its linkage with the performance and degradation mechanism of the W/4H-SiC SBDs are also investigated.

The 4H n-type epitaxial wafers used to fabricate Schottky contacts were supplied by EpiWorld International Co., Ltd. with a carrier concentration N_D = 7.08 × 10¹⁵ cm⁻³ and a thickness of 11.18 μm, and were grown on a highly doped (∼ 1 × 10¹⁹ cm⁻³) substrate layer with a resistivity of 0.018 Ω · cm and a thickness of 350 μm. The SiC wafers were first treated with standard RCA cleaning steps, and sacrificial oxidation was used to improve the SiC interface condition. The oxide layer was etched by dilute HF solution, and the back side Ohmic contact was produced by deposition of a 200-nm-thick Ni film, followed by the rapid thermal annealing (RTA) at 950 °C for 120 s in nitrogen ambiance. Thereafter, a 200-nm-thick W layer was deposited by e-beam evaporation on the surface of SiC epitaxial layer. The Schottky contacts which had circular geometry with a diameter of 500 μm were formed by a standard photolithography process. Six kinds of samples were prepared: one without thermal treatment and the others were further treated by RTA at different temperatures (400 °C, 500 °C, 600 °C, 700 °C, and 1000 °C) for 5 min in vacuum. The contacts were characterized by current–voltage (I–V) and capacitance–voltage (C–V) with the measuring temperature range of 25 °C–175 °C by using an Agilent 1500B source meter unit. X-ray diffraction (XRD) analyses were carried out in order to identify the formed phases and their crystallographic orientations.

Considering the effect of the series resistance R_s, the forward current–voltage characteristics of a Schottky contact obeying the thermionic emission (TE) model are given by (for (V − IR_s) > 3 kT/q)^[20]

The values of n, Φ_B, and R_s are calculated using a method developed by Cheung and Cheung^[22]

Taking the sample annealed at 500 °C as an example, as shown in Fig. 1(b), equation (3) gives a straight line for the data of the downward-curvature region of the I–V–T characteristics shown in Fig. 1(a). Therefore, the slope and y-intercept of a plot of dV/d(ln I) versus I will give R_s and nkT/q, respectively. Using the n value determined from Eq. (3) and the data of downward-curvature region in Eq. (4), a plot of H (I) versus I according to Eq. (5) also gives a straight line with y-intercept equal to n Φ_B. Thus, the values of n, Φ_B, and R_s of the contacts are obtained, respectively.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (color online) (a) The I–V–T plots of W/4H-SiC Schottky contact. (b) The experimental dV/d(ln I) versus I and H(I) versus I plots for the W/4H-SiC Schottky contact at different testing temperatures.

The n, Φ_B, and R_s at different testing temperatures obtained from Fig. 1(b) are shown in Fig. 2. It can be clearly seen that Φ_B increases and n decreases as the testing temperature increases. The temperature dependence of n and Φ_B has been reported in different literatures,^[17,23,24] and it has been explained as the presence of an inhomogeneous Schottky barrier. The series resistance increases with increasing temperature, and similar results were reported by Toumi et al.,^[25] which could be explained by the fact that the main component of series resistivity, epitaxial, and substrate layer increase with increasing temperature.^[6] The resistance at room temperature is somewhat higher than that at high temperature, which is possibly due to the measuring equipment.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (color online) (a) n and ΦB as a function of the testing temperature for the W/4H-SiC Schottky contacts. (b) Rs of the W/4H-SiC Schottky contacts at different testing temperatures.

Applying Tung’s model to our case, we present the plot of nkT versus kT in Fig. 3(a), where the straight line describes the ideal behavior (n = 1). As can be seen, the n’s obtained at different temperatures are fitted by a straight line parallel to that of the ideal case. Such behavior is typical of a real Schottky contact with a distribution of barrier inhomogeneity, and is commonly referred to as the so-called “T₀ anomaly”, while the value of T₀ can be determined by

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (color online) (a) Plot of nkT/q versus kT/q showing the T0 effect. (b) T0 anomaly versus annealing temperature.

According to Tung’s model, there are patches of low barrier (qΦ_B0 − Δ) embedded in a uniform high-barrier height (qΦ_B0), and the deviation is expressed as Δ. By assuming the circular patches with radius R₀, the parameter can be used to describe the barrier inhomogeneity. Considering the pinch-off model, the patch parameter γ is not a constant, Tung and coworkers suggest the Gaussian distribution of γ with a standard deviation σ, and the constant T₀ is given by

In order to identify the formed phases during the annealing process, XRD analyses are carried, and the C–V characteristics at different testing temperatures are also evaluated. The x-ray diffraction spectra of different annealing temperatures are shown in Fig. 4. The capacitance is measured at different reverse bias values at 1 MHz by superimposing an ac voltage on the dc voltage. Taking the sample annealed at 500 °C as an example, the C⁻²–V plots are shown in Fig. 5(a), and the capacitance is given by

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (color online) X-ray diffraction spectra of W/4H-SiC Schottky contacts surface upon different annealing temperatures. The unlabeled peaks at the diffraction angle about 35° are considered to be SiC.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. (color online) (a) C–V measured BH of W/4H-SiC Schottky contacts formed at different annealing temperatures versus different testing temperatures. (b) C–V and I–V measured BH at different testing temperatures of W/4H-SiC Schottky contacts versus different annealing temperatures.

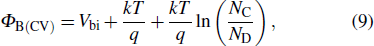The BH’s obtained by C–V method are illustrated in Fig. 5(a), showing testing temperature independence, which means a uniform high barrier.^[26] And the BH’s obtained from Fig. 2(a) (I–V) are also shown in Fig. 5(b) as comparisons.

Figure 4 shows the XRD spectra of W/4H-SiC Schottky contacts formed at different temperatures. For the as-deposited, 400 °C, and 500 °C annealed samples, there are two kinds of space groups of W. The diffraction peaks at 39.96°, 43.78°, 66.60°, 69.56°, and 75.10° can be attributed to the (210), (211), (320), (321), (400), (420), and (421) reflection of W(Pm-3m), respectively, while the diffraction peaks at 40.30°, 58.50°, 73.30°, and 87.06° can be attributed to the (110), (200), (211), and (220) reflection of W(Im-3n), respectively. The intensity of the W(Pm-3m) peak decreases with the increasing annealing temperature, and only the peak of W(Im-3n) exists at the annealing temperature of 600 °C. At the annealing temperature of 600 °C, the appearance of the peaks at 35.60° and 75.06° can be attributed to the (002) and (240) reflections of the formed W₂C phase during the annealing treatment, and the increase of the peak intensity and the emerging peaks of other crystallographic orientations of W₂C phase at the annealing temperature of 1000 °C might be interpreted as further reaction between W and SiC. The Schottky barrier height of W₂C/4H-SiC is about 0.94 eV,^[27] apparently lower than that of W/4H-SiC, thus the sample annealed above 500 °C shows lower BH (obtained from I–V) than that annealed at lower temperature as shown in Fig. 5(b).

The appearance of W₂C at high annealing temperature may lead to more patches with lower barrier height than that at low annealing temperature, which is the reason of higher T₀ for the samples annealed at 600 °C, 700 °C, and 1000 °C, as shown in Fig. 3(b). Thus for the fabrication of W/4H-SiC Schottky rectifier for high temperature application, an annealing temperature of 500 °C may result in the highest BH and lower reverse leakage current.^[6]

The current of the Schottky contact is made up of two components.^[8] One is the current over the entire contact, which has a uniform BH, and the other is an additional current due to the presence of the low-BH patches. At high temperatures, the current is dominated by thermionic emitted transport over the uniform BH and displays a near unity ideality factor. At low temperatures, the low-BH patches dominate at small bias and the ideality factor is larger than 1. As shown in Fig. 5(b), the relative value of BH at high testing temperature tends to accord with the relative value of BH obtained from C–V measurement.

The n, Φ_B, and R_s of several W/4H-SiC Schottky contacts annealed at different temperatures are obtained by I–V–T measurements, and the temperature dependence of the ideality factor and BH indicates the formation of an inhomogeneous barrier. The experimental data are analyzed by the Tung’s model to describe the contact with a homogeneous high-barrier background in which low-barrier patches are embedded. The values of T₀ in Tung’s model are calculated to evaluate the degree of the barrier inhomogeneous. It is found that the degree of the inhomogeneous barrier depends on the thermal annealing temperature, and the 400 °C treated samples have the lowest degree of inhomogeneity of the barrier. The BH of the Schottky contact is related to both the space group of W and the phase composition of W–SiC reaction. The phase of W₂C appears at annealing temperature of 600 °C, resulting in a low BH of the Schottky contact and a high T₀, which means high degree of inhomogeneity of the barrier. The fact that the 500 °C annealed sample has the highest BH at all testing temperatures indicates an optimal annealing temperature for the W/4H-SiC Schottky rectifier for high temperature application. The BH’s obtained from C–V–T are higher than those of I–V–T and are independent of the testing temperature, and are considered as the value of uniform barrier height. At high temperature, the BH obtained by I–V–T measurements tends to be close to the BH obtained from C–V–T, which means the current is dominated by thermionic emitted transport over the uniform BH.