† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11635003, 11025524, and 11161130520), the National Basic Research Program of China (Grant No. 2010CB832903), and the European Commissions of 7th Framework Programme (FP7-PEOPLE-2010-IRSES) (Grant No. 269131).
The tantalum arsenide (TaAs) is a topological Weyl semimetal which is a class of materials of gapless with three-dimensional topological structure. In order to develop a comprehensive description of the topological properties of the Weyl semimetal, we use the density functional theory to study several defects of TaAs after H irradiation and report the electronic dispersion curves and the density of states of these defects. We find that various defects have different influences on the topological properties. Interstitial H atom can shift the Fermi level. Both Ta vacancy with a concentration of 1/64 and As vacancy with a concentration of 1/64 destruct a part of the Weyl points. The substitutional H atom on a Ta site could repair only a part of the Weyl points, while H atom on an As site could repair all the Weyl points.
Weyl fermions are massless opposite chiral quasiparticles with spin 1/2,[1–3] and the material containing this particle is called Weyl semimetals (WSM). The characteristic of WSM with a gapless metal is topological invariant, which is different from the classification of topological phases of insulators. More significant characteristic is that the crossing points of the valence and conduction bands as Weyl point[4–6] are degenerate at the Fermi level.[7–9] Weyl nodes are associated with chiral and protect the gapless surface state on the bulk boundary of the sample.[10] Theory predicts the interesting physical properties of WSM, such as the negative magnetoresistance and the discontinuous Fermi arcs due to the chiral anomaly of Weyl nodes.[11–23] In Ref. [24], Rn2Ir2O7, pyrochlore, with all-in or all-out magnetic structure,[25] possessing 24 pairs of Weyl points, was initiated associated with WSM in condensed-matter materials. The Weyl points appear when this system undergoes the magnetic ordering transition. HgCr2Se4,[26] a relatively simple system, exhibited a pair of double-Weyl points[10,27–30] when this system was in a ferromagnetic phase with the appearance of quadratic band crossing. Recent band structure calculations predict a new family of WSMs which includes TaAs, TaP, NbAs, and NbP, possessing 12 pairs of Weyl points[27,31] in the transition-metal monoarsenides or monophosphides.[12,27,29,32–35] In their lattice forms, these systems hold the time-reversal symmetry, while breaking the inversion symmetry. For all the properties mentioned above, of particular interest are the topological surface states of TaAs and isostructural crystal compounds TaP, NbP, and NbAs, which are experimentally investigated by the angle resolved photoelectron spectroscopy (ARPES)[29,36,37] pointing to the existence of the Weyl nodes.[27] Moreover, there is no magnetic effect caused by the complexity of the domain, or more directly, from their bulk electronic band structures by means of sensitive ARPES measurements.[36,38]
All of the above four materials have very similar band structures. First-principles calculations point to TaAs as a topological semimetal. In real materials, this is of great help to the exploration of Weyl physics. TaAs symbolizes a novel topological state of matter arousing interest in fundamental physics, and it has been verified to exhibit unique electronic properties and energy band structures as well as high carrier mobilities.[39] However, knowledge about its electronic properties of defects lags far from the perfect lattice.
As an effective material modification technique, ion beam implantation plays an important role in the study of defective crystals. The modified properties are from defects generated. It is practical interest to investigate the defective properties of these topological materials. When the exposure of this material to H irradiation, it is worthwhile mentioning that there are various kinds of defects in TaAs irradiated by H. In the present study, we particularly focus on these static point defective structures. Investigation shows that the possible point defects which can be produced are: interstitial (IH), vacancies (VTa and VAs), the substitutional H atom on a Ta site (HTa) and on an As site (HAs). As we know, HTa and HAs may not exist in thermodynamic equilibrium, while they can appear in the ion implantation process. In the current work, the defect concentration is 1/64 in all defective lattices. The effect of defects on topological properties was studied by analysing the dispersion curves and density of states of different defects.
In the process of optimizing crystal structure, we use Perdew–Burke–Ernzerhof (PBE) to parameterize the exchange–correlation functional within a generalized gradient approximation.[41–45] In the present study, since spin–orbit coupling (SOC) may conceal the Weyl band-crossings in this system, we can not easily find out the Weyl band-crossings different from the other points, which is inconsistent with our discussion about the influence of defects on the topological properties. Taking the above situations into account, we neglect SOC in the calculation.
In the task of customized geometry optimization, we select the convergence tolerance energy to less than 5.0 × 10−6 eV, set the cut-off energy as 600 eV, and choose K-space mesh to less than 0.02 nm−1 in each direction. The calculations were carried out by using the software CASTEP for the first-principle calculations.[46] We have chosen the ultrasoft pseudopotential which facilitates faster calculation to meet the requirements. Since Weyl point is mainly correlated to valence electron, the description of core electron is implemented using pseudopotential.
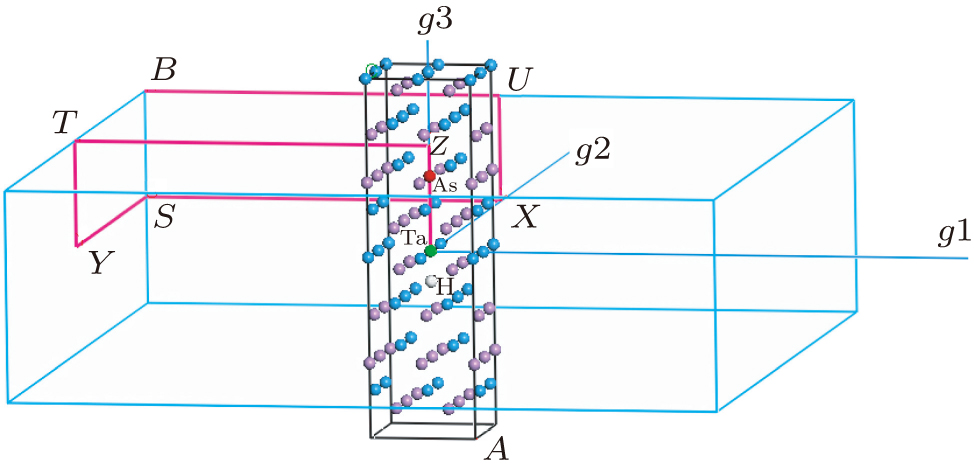
The crystal texture of TaAs is a body-centered-tetragonal structure, and its space group is I41md (No. 109) which lacks inversion symmetry and nonsymmorphic. The other super-cell of defects are Pmm2 (No. 25) symmetrical space group. The measured lattice constants in the experiment are a = 3.4348 Å, b = 3.4348 Å, and c = 11.6410 Å.[27,40] Wyckoff positions for Ta and As are (0, 0, 0) and (0, 0, 0.417), respectively. The primitive cell parameters are based on experimental parameters, and the cell parameters were optimized in order to obtain an energy minimized lattice structure. After cell optimisation, we obtain the lattice constants a = b = 3.487932 Å and c = 11.72503 Å. Due to the small variation of the cell parameters, the position of the atom is optimized more precisely. Optimising u = 0.41535 for the As site results in good agreement between our calculations and experiment. We set the constants for the perfect and defective 2 × 2 × 2 super-cell as a = b = 6.8696 Å and c = 23.282 Å. The optimized lattice parameters are listed in Table
| Table 1. Lattice parameters of perfect and defective crystals. . |
Figure
Before calculating the defect formation energy, we firstly optimize the energy for the five defects. Calculating the crystal energy of the optimized structure, we find that the energy differences for IH, VTa, VAs, HTa, and HAs after and before optimization are −0.13 eV, −0.37 eV, −0.06 eV, −2.93 eV, and −0.37 eV, respectively.
The defects have an effect on the electronic band structure, therefore various properties of the material may be affected. We calculate the crystal defect formation energy ΔH using the energy formula
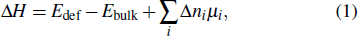 |
Five defect formation energies are calculated similar to Refs. [47] and [49], summarized in Table
| Table 2. Defect formation energy of various defects. . |
After the H ions have slowed down, the H ions can stop in a cage or stop in a vacancy center and the vacancies can be annihilated. That the formation energy of IH is −3.26 eV means that the most stable defective structure is IH. The minus sign of formation energy means that H atoms are possible to stay in one of the cages. According to Table
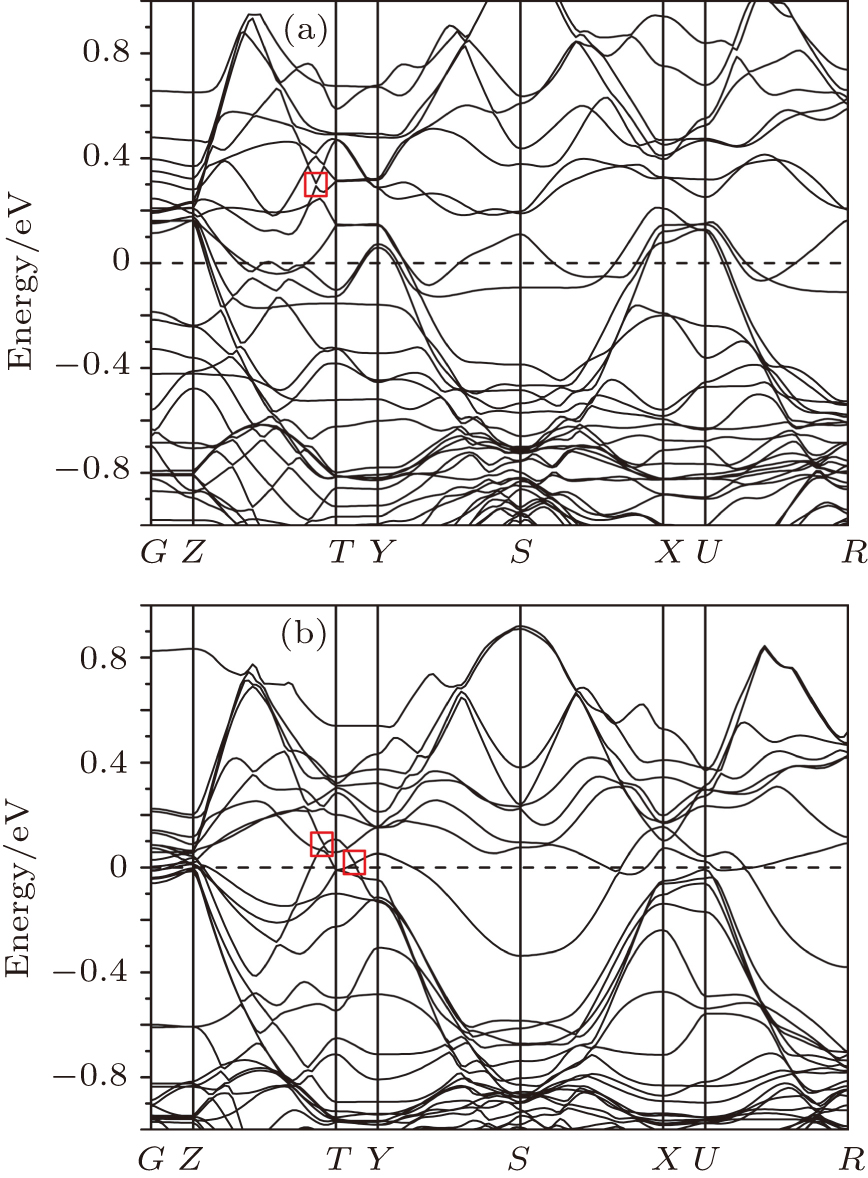
We compute how crystal defects influence the position of the Fermi level relative to the so-called Weyl points. As can be seen from Fig.
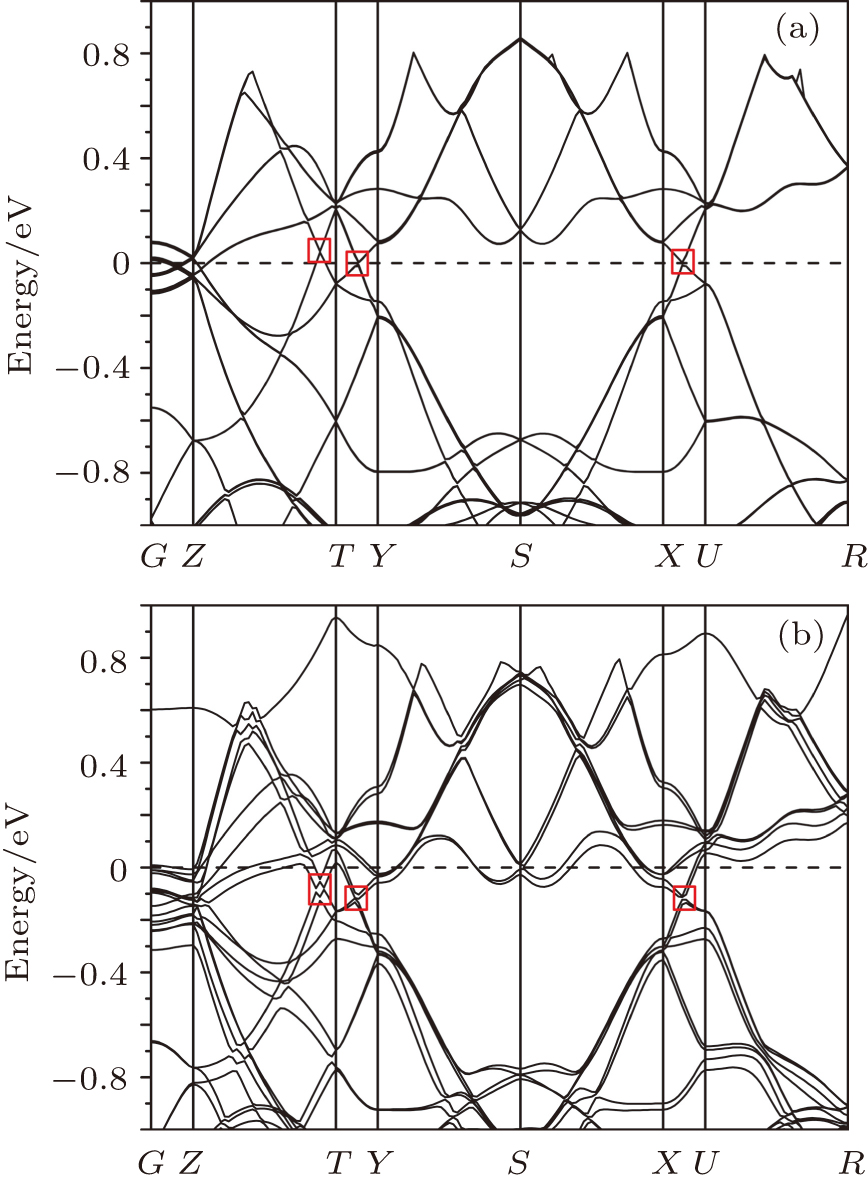 | Fig. 2. (color online) Dispersion curves of (a) Ta32As32 and (b) HTa32As32. The Fermi level in panel (b) is almost 0.1 eV above that in panel (a). The square frames indicate the Weyl points. |
IH is represented by HTa32As32 with the symmetry group of Pmm2, in which H atom is an interstitial atom. The dispersion curve of a perfect super crystal is shown in Fig.
VTa is represented by Ta31As32 with the symmetry group of Pmm2, in which a Ta atom is removed from the center of the cell, and then a Ta vacancy cell is produced. The calculated dispersion curve of Ta31As32 is plotted in Fig.
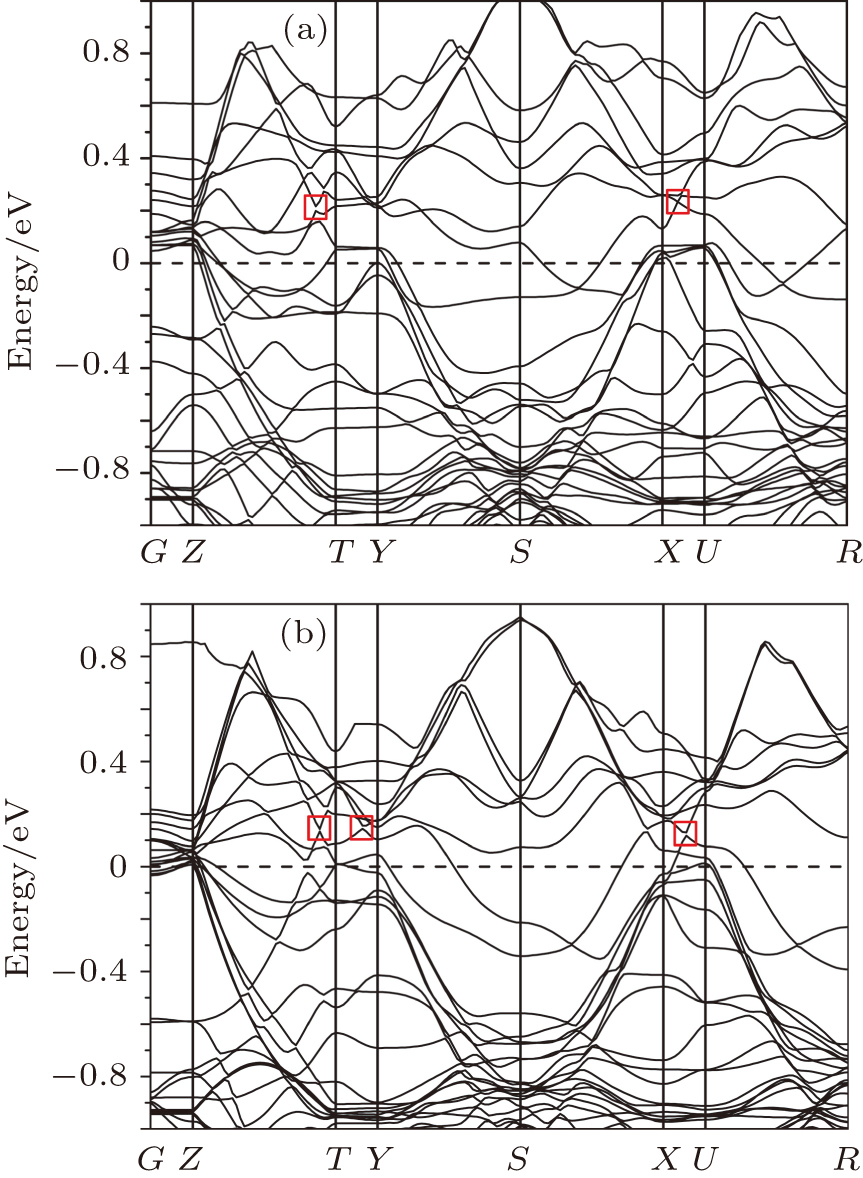
VAs is represented by Ta32As31 with the symmetry group of Pmm2, in which an As atom is removed from the center of the cell, and then an As vacancy cell is produced. The calculated dispersion curve of Ta32As31 is presented in Fig.
HTa is represented by HTa31As32 with the symmetry group of Pmm2, in which H atom substitutes a Ta atom on the corresponding site. The calculated dispersion curve of HTa31As32 was plotted in Fig.
HAs is represented by HTa32As31 with a substitutional H atom on an As site, which has the symmetry group of Pmm2. The calculated dispersion curve of HTa32As31 is plotted in Fig.
In this case, all the Weyl points are identified, as seen in Fig.
As shown in Fig.
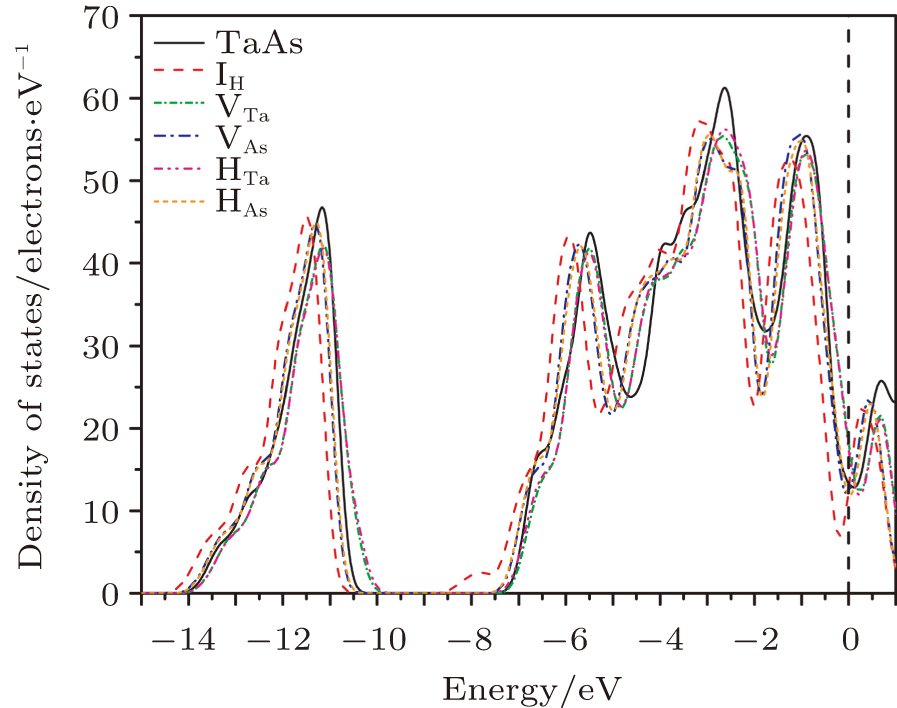
The density of states curves of different orbits of the crystals are shown in Fig.
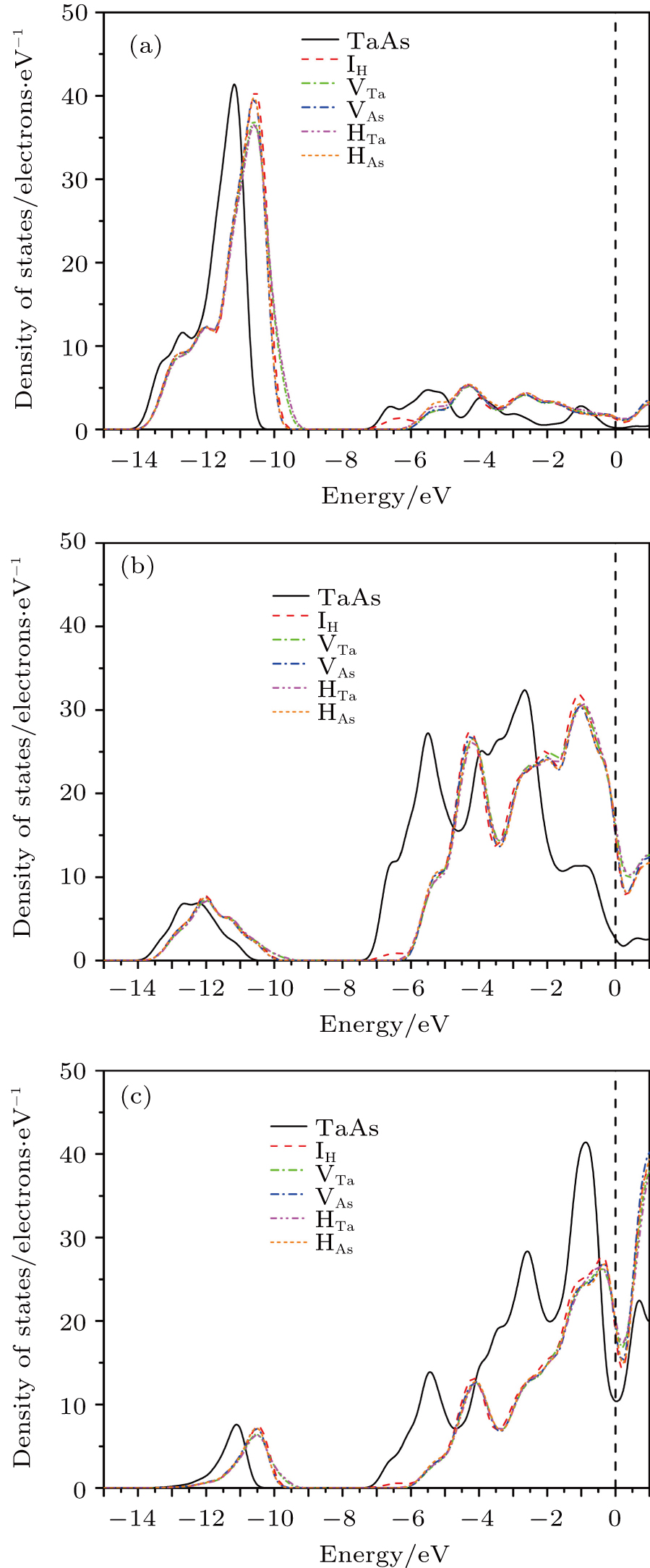 | Fig. 6. (color online) Partial density of states of six super-cells of (a) s-orbit, (b) p-orbit, and (c) d-orbit. |
In addition, the specific focus is that the distribution of density of states near the Fermi level is destroyed by the defective atomic orbit hybridization.
The first principles calculations are performed to investigate its defect formation energies and explore the changes of topological properties, when H is injected into the perfect super-cell of TaAs. To the best of our knowledge, vacancies are more difficult to be formed than other defects. H is more efficient to repair the topological properties of As vacancies than Ta vacancies. The simulation results show that different defects have different influences on the topological properties. As H acts as an interstitial atom, it can shift the Fermi level. This phenomenon is interesting and further effort is required to understand the reason for shifted the Fermi level. Ta vacancy with a concentration of 1/64 or As vacancy with a concentration of 1/64 can destruct a part of the Weyl points. H atom on the Ta site can repair a part of the Weyl points, while the defect of substitutional H atom on an As site repairs all the Weyl points. The densities of states of HTa32As31 and Ta32As32 are almost the same near the Fermi level. A comparison of the curves of the density of states in different structures indicates that d and f electrons of Ta atom are most important to topological properties. The location of Weyl points is independent of types of defects. In addition, the Fermi level can be tuned by concentrations of vacancies and interstitial.
On the one hand, our results suggest that the Fermi level is regulated by changing the concentration of vacancy defects and interstitial atoms in TaAs, which may potentially be used to better separate electrons and holes in WSM. That the concentration of defects adjusts the Fermi level, therefore, provides a powerful method for topological material and is broadly applicable to a variety of systems. On the other hand, by thorough theoretical analysis, hydrogen can repair damaged Weyl points, which suggests its promising applications in reinforcing topological properties of materials and realizing electronic transmission with low energy consumption.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] |