† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61571319).
The application of surface acoustic waves (SAWs) for thickness measurement is presented. By studying the impact of film thickness h on the dispersion phenomenon of surface acoustic waves, a method for thickness determination based on theoretical dispersion curve v(fh) and experimental dispersion curve v(f) is developed. The method provides a series of thickness values at different frequencies f, and the mean value is considered as the final result of the measurement. The thicknesses of six interconnect films are determined by SAWs, and the results are compared with the manufacturer’s data. The relative differences are in the range from 0.4% to 2.18%, which indicates that the surface acoustic wave technique is reliable and accurate in the nondestructive thickness determination for films. This method can be generally used for fast and direct determination of film thickness.
Films are widely applied in aerospace, automotive manufacturing, biomedical engineering, and microelectronic industries.[1–4] In all such fields, the film thickness is one of the most important parameters for film quality evaluation. Yadav studied the influence of film thickness on structural, optical, and electrical properties of spray deposited antimony doped SnO2 thin films.[5] Ren et al. studied the influence of thickness upon the interfacial water at the solid-liquid interface.[6] Yang et al. analyzed the influence of nanofilm thickness on the elastic properties of B2-NiAl.[7] So the film thickness is not only a parameter that characterizes the geometrical dimensions of the films, but also greatly affects the function and lifetime of the films. Therefore, film thickness determination is an important requirement in many fields of technology.
In order to keep the function of the films after thickness measurement, many nondestructive testing methods have been proposed to measure the film thickness, including eddy current, spectroscopic ellipsometry, and x-ray transmission.[8–15] These methods work well, but they are all restricted to certain types of materials. The eddy current method is more suitable to measure the thickness of the non-conductive coating on the non-magnetic metal substrate.[8–10] The spectroscopic ellipsometry is an optical method. The measured material should be transparent.[11–13] The x-ray transmission needs the absorption coefficients of the film and substrate to have obvious differences. The limitation for its wide application can be found when the chemical composition of the film is close to that of the substrate.[14,15]
Surface acoustic waves (SAWs) are dispersive during propagating on a layered structure, the surface acoustic waves with different frequencies have different propagation velocities. Due to this feature, the surface acoustic wave method can be applied to film thickness determination. This method is fast, simple, and non-destructive.[16–18] In addition, the propagation of SAWs is hardly limited by the material. So this method is suitable to determine the film thicknesses of most materials.
In this paper, the relationship between the geometrical parameter thickness and the dispersion phenomenon of surface acoustic waves is analyzed. Accordingly, a thickness calculation method is developed by using the theoretical dispersion curve v(fh). The thickness calculation of two standard SiO2 films with this method is described in detail. In addition, four low dielectric constant (low-k) samples are also investigated in this study. The results of the six samples are compared with the manufacturer’s data. Comparing the results shows that the thicknesses of the interconnect films can be sensitively detected by the SAWs measurement.
Surface acoustic waves propagate along the surface of a material. The penetration depth of the wave is defined to be equal to the wavelength λ and it reduces with increasing frequency.[16] In a homogeneous and isotropic bulk material, the wave phase velocity v depends on the material parameters: Young’s modulus E, density ρ, and Poisson’s ratio σ, and it is independent of the frequency f of the wave.[19,20]
In the film/substrate structure, the phase velocity v of the waves depends on the film and substrate material parameters and the frequency–thickness product fh.[21,22] The surface acoustic waves are dispersive, and the dispersion phenomenon is resulted from the different SAW phase velocities in the film and substrate materials. Figure
In addition to the frequency, the film thickness has the same effect on the phase velocity of SAWs. The increase of the film thickness can expand the influence of the SiO2 film on SAWs propagation. So the increases of the frequency and the film thickness together result in the change of the wave velocity. According to the physical principles of the elasto-dynamic theory, the phase velocity v of the waves is a function of the frequency–thickness product fh on the condition that the material parameters of the film and substrate are determinate.
For the thickness determination, the SAWs experiment can provide the v (f) curve of the sample. This curve contains information about the film thickness. With the material parameters of the sample, the relationship between the phase velocity v and the frequency–thickness product fh can be calculated. By using the theoretical dispersion curve v(fh) and experimental dispersion curve v(f), the film thickness can be obtained.
Figure
Two standard SiO2 films with different thicknesses are firstly tested by the SAWs technique to check our method. These films are grown by thermal oxidation on Si substrate. The material parameters of the standard SiO2 film include Young’s modulus E = 72 GPa, density ρ = 2.2 g/cm3, and Poisson’s ratio σ = 0.17. Surface acoustic waves are generated on the sample surface and arranged to propagate in the [110] direction of silicon.
In order to obtain the experimental dispersion curve, the electric signals ui(t) (i indicates different laser position) are detected at two different distances x1 and x2 away from the line-shaped laser source. The SAWs signals of SiO2 I detected at two different positions are shown in Fig
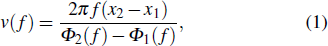 |
Figure
 |
 |
A method to determine the thickness is developed by combining the theoretical dispersion curve v(fh) and experimental dispersion curve. Because the two SiO2 films employed in this research have the same material parameters, the same theoretical dispersion curve v(fh) is used to calculate the thicknesses of the films. Figure
 |
 | Fig. 5. (color online) The theoretical dispersion curve v(fh) used to determine the thicknesses of SiO2 films. |
Because theoretical dispersion curve v(fh) contains many data points, a series of thickness values can be calculated from different data points. Table
| Table 1. The data of the theoretical curve, the frequencies fexp of two experimental dispersion curves, and calculation results of the two SiO2 films. . |
Low dielectric constant (low-k) materials are very important to decrease the RC delay in interconnects of integrated circuits.[24,25] The combination of the low-k insulator with lower resistivity metal of Cu is widely used in high speed ultra large-scale integration devices.
The thicknesses of four low-k samples are measured by the proposed SAWs method in this study. Figure
| Table 2. Material parameters of porous and dense black diamond low-k samples. . |
The thicknesses of these samples determined by the SAWs method and the manufacturer’s data are listed in Table
| Table 3. Summary of thicknesses obtained from the surface acoustic wave method and manufacturer’s data. . |
The surface acoustic wave technique is applied to measure the thicknesses of films of ULSI. A thickness calculation method is developed based on the union of experimental dispersion curve and theoretical dispersion curve v(fh). This calculation method is very simple and fast. A series of thickness values can be calculated at different frequencies f of the experimental dispersion curve. The mean value is considered as the final result of the measurement. So there is another advantage of the method that multiple thickness values can reduce the uncertainty of single data and increase the reliability of the measurement result. Six interconnect films are employed to verify our method. The results of these films are compared with the manufacturer’s data. For these six films, the relative differences between the measurement results and manufacturer’s data are only in the range from 0.4% to 2.18%. The remarkable agreement of the contrast results shows the potential and reliability of the surface acoustic wave technique.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] |






