Surface plasmons polaritons can break the diffraction limit, enabling nanoscale control of light and facilitating promising applications involving fabrication of highly integrated nanophotonic devices. Over past decades, a variety of devices based on metal plasmonics such as Mach-Zender interferometric modulators,^[1,2] light amplifiers,^[3] all-optical switches,^[4,5] and even integrated photonic systems^[6,7] have been successfully demonstrated both theoretically and experimentally. However, the large Ohmic losses in metal plasmons is a major obstacle limiting their use in nanophotonics applications.^[8]

In the ongoing search for the next generation of plasmonic materials,^[9] graphene is a very promising candidate. Due to its unique electronic band structure in which conical-shaped conduction and valence bands meet at the Dirac point,^[10–13] graphene exhibits extraordinary optical properties such as strong and broadband light-graphene interactions. The easily tunable conductivity of graphene either via chemical doping or in situ electrostatic gating^[14,15] has great potential in designing tunable optical functions or devices, such as engineered Bloch waves,^[16] near-perfect light absorber^[17] and the tunable optical bistability.^[18,19] The Dirac Fermions features of carriers also result in the graphene plasmons (GPs) having very limited intrinsic loss^[20] and ultra-high field confinement, where the wavelength has shrunk more than 100 times compared to light in free space.^[21] Based on these advantages, a series of two-dimensional sub-wavelength graphene plasmonic devices, including light modulator,^[22] plasmonic waveguides,^[23] planar absorbers,^[24] optical switches,^[25] optical splitters,^[26,27] and filters^[28,29] have been studied. Waveguide filters for wavelength selectivity and noise filtering are key devices for signal processing. Recently, waveguide filters with different structures including teeth-shaped, band-disk-band and band-ring-band^[30–32] have been studied. These filters always contain cavities approximately 2- to 3-fold larger than the width of the waveguide, which implies they have low spatial utilization and are inappropriate for largescale integration.

In this paper, we designed an ultra-compact plasmonic filter that was directly integrated in a graphene waveguide. A rectangular hole was introduced in the graphene nanoribbon waveguide to act as a resonant cavity (as shown in Fig. 1(a)). This band-pass filter was studied using the finite-difference time-domain (FDTD) method, which showed that the frequency response could be tuned by the cavity size and Fermi energy (E_F) of the graphene (from 20 to 35 THz). These results are corroborated by coupled mode theory (CMT) calculation.^[33]

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. (color online) (a) Schematic of the graphene plasmonic waveguide filter. A rectangular hole in the nanoribbon acts as a filter. Gate voltage V is used to tune the Fermi level of the graphene. We set SiO2 as the substrate with the dielectric εsub = 4. The width, length, and thickness of SiO2 substrate are 300 nm, 470 nm, and 100 nm, respectively. The dielectric of air on the top of graphene is εair = 1. (b) Top view of the plasmonic waveguide filter. The length and width of the cavity are l and d, respectively. Width of the waveguide is W. Ports 1 and 2 are source port and transmission port, respectively. The distance between these two ports was L = 450 nm. (c) Effective refractive index (neff) of the modes supported by graphene ribbons with different widths. The Fermi level of graphene is EF = 0.35 eV. The mode frequency is 20 THz. Inset shows the EZ profile of the two modes supported by the graphene ribbon with W = 150 nm. The cut-off width of mode #2 is 118 nm. (d) Effective refractive index (orange) and corresponding loss (blue) of mode #1 as a function of incident frequency. The width of ribbon is 50 nm.

A schematic of the designed graphene filter is presented in Fig. 1(a). A graphene nanoribbon acts as plasmon waveguide and supports GPs propagation in the x direction. A rectangular cavity etched in the middle of the nanoribbon (in the y direction) acted as a filter. When the GPs reach the cavity, they are suppressed by reflection and scattering or allowed to transport depending on their frequencies. As shown in Fig. 1(b), the width of the graphene nanoribbon is W, and the width and length of the cavity are d and l, respectively. Here, the ribbon width W was set as 50 nm. The width of the nanoribbon around the cavity is (W − d)/2 and was designed to be more than 5 nm, which can be considered as armchair graphene nanoribbons and still exhibit metallic behavior at room temperature.^[34] We proposed tuning the carrier density of the graphene using a back gate voltage (V) as shown in Fig. 1(a).

We employed the FDTD method to simulate the transmission spectrum of the GP waveguide filter. Here, the graphene ribbon was modeled as a two-dimensional plane with the surface conductivity of σ(ω, Γ, μ_c, T). The surface conductivity contains the interband and intraband terms σ(ω, Γ, μ_c, T) = σ_intra + σ_inter. With an angular frequency ω, the intraband and interband terms are evaluated using the following formula:

For confined plasmons supported on graphene ribbons, there are two plasmon waveguide modes:^[35] one is the edge GP mode which is supported by a semi-infinite graphene ribbon (EGSP) and is well known to occur at the edge in graphene ribbon. The other one is the waveguide GP mode supported by infinite two-dimensional graphene sheets (2DGSP). When graphene sheets are modified into ribbon and the width decreases to tens of nanometers, the 2DGSP mode disappears, and only the edge mode remains. Compared with the 2DGSP, the EGSP has a higher effective refractive index,^[36] which means we can achieve a higher concentration and transmission of electromagnetic field in an ultra-compact plasmonic device. Mode #1 and mode #2 shown in the inset of Fig. 1(c) arise from the symmetric and anti-symmetric hybridization of the EGSP mode, respectively. As displayed in Fig. 1(c), the n_eff–W curve for mode #1 lies above that for mode #2, implying that the former is more tightly confined. For the configuration considered in this paper, mode #2 will be cut off if the ribbon width is smaller than 118 nm at 20 THz, only mode #1 exists, and the cut-off width for mode #2 diminishes when the frequency increases.^[37] Figure 1(d) shows the effective refractive index of mode #1 as a function of incident frequency, and as a function of the loss both increase because of the stronger field confinement at a higher frequency.

According to previous mode analysis, we know that a 50 nm wide ribbon can support the EGSP mode #1, which is emitted from the source port (Port 1) and propagates along the x direction. Meanwhile, the transmission port (Port 2) was set to get the transmitted GPs on the right side of the cavity as depicted in Fig. 1(b). The distance between Ports 1 and 2 is 450 nm. The transmission is defined as T = P_Port2/P_Port1, where P_Port1 represents the incident power and P_Port2 is the transmission power. We employed a metal boundary condition in the y and z directions, and the perfectly matched layer boundary condition was used in the x direction. The minimum FDTD mesh size in the y direction was set as 1 nm.

Figure 2(a) presents the numerically calculated GP transmission spectra of complete (d = 0, green line), broken (d = W, orange line) and patterned (d = 40 nm, blue line) graphene nanoribbons within the frequency range from 1 to 36 THz. As shown, for both the complete and broken graphene waveguides, the transmission of GPs did not present with the band-pass feature. The nearly zero transmission of the broken graphene (orange) implies the GPs were unable to propagate through the gap. However, obvious band-pass features occurred when the gap was replaced with the cavity. There are two resonance peaks at 19.41 THz and 31.69 THz. The transmittance of the GPs at the resonance frequencies reached 80%, while the rest of GPs are rejected outside the resonance frequency range. In the long wavelength limit (λ → ∞), GPs can pass through the graphene waveguide without the influence of the cavity because the wavelength is far larger than the size of the cavity, which causes the diffraction. It is also observed that, as the incident frequency increases, the transmittance gradually decreases. This is consistent with the condition of the GP waveguide (green) and is due to larger GP loss at high frequencies. These results can be understood by exploiting the electromagnetic field distribution in the cavity filter. Figures 2(b)–2(d) depict the electric field distributions of E_z at the frequencies of peaks 1 and 2 and the dip (19.41, 27.26, 31.69 THz, respectively). It was found that GPs can pass entirely through the cavity at the peak frequencies while the field intensity in the right side of waveguide is much weaker at the dip frequency. The resonance modes emerging around the nano-cavity were clearly observed through the magnetic field distribution of H_z at 31.69 THz in Fig. 2(e).

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. (color online) (a) Graphene plasmon (GP) transmission spectra on graphene ribbon (green), filter (blue), and broken graphene ribbon (orange). l = 40 nm, d = 40 nm, W = 50 nm, and EF = 0.35 eV. Red dots denote the coupled mode theory results for the filter. Insets are the sketch maps of the graphene waveguide. (b)–(d) Ez field distribution around the filter at 19.41 THz (peak 1), 27.26 THz (dip), and 31.69 THz (peak 2). (e) Hz field distribution at 31.69 THz (peak 2). The cavity can be regarded as a ring resonator, and Li and Lo are the inner and outer perimeters of the cavity. τs stands for scattering loss between the waveguide and cavity. Es represents the amplitudes of the electric field of the resonant modes around the hole.

To further understand the feature of the filter, the CMT was adapted to analyze its behaviors. This cavity filter was considered a simplified band-ring-band (BRB) resonator as shown in Fig. 2(e). The evolution of fields E_s can be described as follows:^[38]

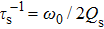
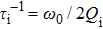
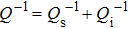
Combining Eqs. (4) and (5), the transfer function can be given by

We investigated the influence of the geometric parameters of the cavity on the resonant frequency. The calculated transmission spectra of the GP filter with varied l and d are displayed in Figs. 3(a) and 3(c). As shown, the resonance frequencies obviously shift to red as l and d increases (indicated with black arrows). For the BRB resonator as shown in Fig. 2(e), the GPs can travel clockwise and anticlockwise simultaneously around the cavity, and the resonating frequency can be obtained by the following equation:^[39]

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (color online) (a), (c) Transmission spectra of GPs filters with different cavity lengths (l) and widths (d), respectively. (b), (d) The resonant frequencies of peaks 1 and 2 extracted from panel (a) and (c) plotted as a function of the equivalent radius (Ri + Ro)/2.

The working frequency of this cavity filter could be electrically tuned in situ. Figure 4(a) depicts the evolution of its transmission spectrum as the change of graphene E_F. The resonance positions display an obvious blue-shift with increasing E_F. For example, peak 1 shifts from 16.37 to 22.88 THz as E_F increases from 0.25 to 0.5 eV. The resonance frequencies of peaks 1 and 2 are extracted and plotted in Fig. 4(b). The trend can be well fitted with ω_r proportional to . This behavior is similar to the dispersion of graphene plasmon which is calculated as^[1,10]

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (color online) (a) Transmission spectra of GPs waveguide filter with different Fermi levels (EF). For the cavity, l, d = 40 nm. (b) The resonant frequency of peaks 1 and 2 in panel (a) plotted as a function of Fermi levels.

Next, we investigated the connection between the filter efficiency and basic parameters of the cavity filter. We defined the height difference (HD) between the resonance peak and dip as the filter efficiency as depicted in Fig. 5(a),^[29] i.e., the largest transmission difference between the passband and stopband. A higher HD indicates less attenuation at the passband and better filter performance. Figure 5(a) shows the transmission spectra of the filter for different qualities of graphene, which is evaluated by the scattering rate (Γ). Figures 5(b)–5(e) present the HD as a function of the scattering rate (Γ), Fermi level (E_F), length of cavity (l), and width of cavity (d), which are extracted from Fig. 5(a), 4(a), 3(a), and 3(c), respectively. Of these parameters, HD only strongly depends on the scattering rate Γ. As shown in Fig. 5(b), the cavity quality factor Q_i decreases rapidly as Γ increases because more intrinsic loss is introduced to the plasmon by scattering from detects. Coupling quality factor Q_s increased slightly when Γ increases, but is not big enough to compensate for the scattering loss. The HDs barely change with d, l, and E_F. In Figs. 5(c)–5(e), we set Γ = 0.0001 eV and HD is kept steady at about 0.7. These simulation results suggest that this filter’s performance is quite stable.

Fig. 5.

Figure Option ViewDownloadNew Window

Fig. 5. (color online) (a) Transmission spectra of GPs waveguide filter with different scattering rates (Γ) of graphene. (b) Height difference (orange), cavity quality factor (blue), and coupling quality factor (green) as a function of scattering rate for peak 1 in panel (a). (c)–(e) Height difference as a function of Fermi level, length of cavity, and width of cavity, respectively, for peak 1. The values are extracted from Figs. 4(a), 3(a), and 3(c), respectively.

In conclusion, we constructed an ultra-compact, tunable and highly efficient GPs waveguide filter using a simple rectangular cavity configuration. The filter exhibits a stable band-pass filtering effect with transmission reaching ∼ 80%. The working frequency of the filter could be tuned in a large frequency range based on cavity geometric design and in situ electrically gating. The efficiency of the filter is closely related to the graphene quality and performs very stably with different graphene Fermi levels and cavity geometries. These numerical results are corroborated by the CMT. The as-proposed cavity filter has promising applications in ultra-compact nanoscale optical circuits.