† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 21676041).
The expressions of interface free energy (IFE) of composite droplets with meniscal liquid–air interface in metastable state on micro/nano textured surfaces were formulated. Then the parameters to describe the meniscus were determined based on the principle of minimum IFE. Furthermore, the IFE barriers and the necessary and sufficient conditions of drop wetting transition from Cassie to Wenzel were analyzed and the corresponding criteria were formulated. The results show that the liquid–air interface below a composite droplet is flat when the post pitches are relatively small, but in a shape of curved meniscus when the piteches are comparatively large and the curvature depends on structural parameters. The angle between meniscus and pillar wall is just equal to the supplementary angle of intrinsic contact angle of post material. The calculations also illustrate that Cassie droplets will transform to Wenzel state when post pitch is large enough or when drop volume is sufficiently small. The opposite transition from Wenzel to Cassie state, however, is unable to take place spontaneously because the energy barrier is always positive. Finally, the calculation results of this model are well consistent with the experimental observations in literatures for the wetting transition of droplets from Cassie to Wenzel state.
Droplets on micro/nano textured surfaces may appear in the states of Cassie (with flat liquid–air interface beneath), Wenzel, or composite (with curved liquid–air interface) as shown in Fig.
 | Fig. 1. Schematics of Cassie (A) with flat liquid–air interface beneath, Wenzel (B), and composite droplet (C) with curved liquid–air interface on a textured surface. |
Most researchers considered the shape of liquid–air interface beneath a composite droplet as a plane or a straight line (Fig.
The condensed drop shapes on nanostructures observed by Rykaczewski[10] showed that the liquid–air interface between posts with small pitches indeed appeared in arc. Whereas the experiment by Ensikat et al.[20] indicated that the liquid–air interface between posts with large pitches appeared in plane without obvious bending, and curvature only existed near pillar walls. Meanwhile, a clear meniscus would appear when a droplet was acted by external pressure or electric wetting force.[11–15] Therefore, the shape of bending liquid–air interface is relevant to not only structural parameters but also the action of external forces. When a droplet is not acted by external pressure, its bottom liquid–air interface profile is not necessarily always an arc.
Minimizing of interface free energy (IFE) of droplets is often used to determine its wetting state,[1,3,21–25] including equilibrium contact angle etc. Multi-peak values[2,22] may exist for the IFE of droplets on textured surfaces. Locally minimum and globally minimal IFE are corresponding to the metastable and the most stable drops, respectively. A metastable droplet is unable to transform to the most stable state spontaneously because there is an energy barrier to overcome. Consequently, Cassie drops or composite droplets can exist stably although they are not in the lowest energy state.[27] Only when certain pressure or electric wetting force[11–15,17] acts on a metastable drop, it may transit to wetted state.
Droplet IFE is relevant to the shape of liquid–air interface, but almost all IFE calculations did not involve the curvature of the interface.[1–3,21–25] Only very few two dimensional models[5] were based on the bending interface without three dimension calculations so far. Additionally, only contact angles were generally calculated by means of IFE minimum[2,24] while the parameters describing meniscus were not solved until today.
On the other hand, the mechanism of droplet C–W transition has been investigated heavily,[3–9,11–15,17–19,22,25–41] which is classified into two types, external force driving and spontaneous evolution. External forces include static pressure or hydraulics pressure,[11,12,15,17,18,40] impact force of droplet landing from high place[38,42] or deceleration force,[41] and static electricity wetting force.[13,14,34] The effect of gravity could be ignored for a droplet if its scale is less than the capillary length.[9] The so-called spontaneous transition means the collapse of a Cassie droplet on structural surface not by external force, but only by the interaction between the droplet and the textured surface. For example, an evaporating droplet on a rough surface will convert from composite state to Wenzel state spontaneously when its volume decreases to a critical value.[7,9,17,35,36] Until today however, this mechanism of the spontaneous transition is still not clear. There are a few conflicted interpretations, including the Laplace pressure inside droplets as the transition driving force,[7,15,37,38] the external force overcoming the Laplace pressure,[17] the gravity of droplets as driving force[4,6,39] etc.
It is generally considered that the C–W transition needs to overcome a energy barrier,[3,5,19,25,27,30–32,43,44] and the barrier of drop evolution from Wenzel to Cassie state (W–C) is always greater than the one of C–W transition.[28,31] Therefore, W–C alteration is more difficult and the two transition processes are considered irreversible.[28] Moreover, contact angles were usually regarded as constants when calculating energy barriers,[30,32,43,44] which would lead to energy barriers always positive.[27,43,44] For instance, Zheng et al.[32] derived that W–C barrier was adhesion work while C–W barrier was wetting work. The forever positive of C–W barrier means the transition can not be completed spontaneously unless the action of an external force. But the truth is that the C–W transition is able to be accomplished spontaneously for small droplets sitting on posts with relatively large pitches. Consequently, C–W energy barriers might disappear or become negative[25] under certain conditions. In a word, more reasonable calculation of C–W and W–C energy barriers is still absent.
A three-dimensional (3D) model of the meniscus beneath a sessile droplet on textured surface was founded in this study. The droplet IFE was formulated with multi variables, and the parameters depicting the meniscus of a composite droplet in metastable state were determined based on the principle of IFE minimizing. Finally the energy barriers of C–W and W–C transition were calculated and the necessary and sufficient conditions of C–W transition were figured out.
The metastable and most stable states of a sessile droplet are corresponding to its IFE locally and globally minimal respectively. In many cases although the IFE of a metastable composite drop with its IFE locally minimal is greater than that when it is in Wenzel state, the composite droplet still does not transit to Wenzel state because of the existing of energy barrier. Therefore, sessile drops usually appear in composite state suspending on pillars. The shape and the minimum IFE of a composite droplet are analyzed below. As shown in Fig.
The above mentioned multi variables, θ, rs, x, R, ϕ, hx, and l, are used to describe the meniscus of a metastable droplet on textured surfaces. These parameters can be determined based on the method of drop IFE minimum. In order to calculate the IFE, the expressions of meniscus area and volume into textures beneath a droplet have to be established firstly.
We used the seven varables to dispict the mensicus beneath a droplet on textured surfaces, i.e., θ, rs, x, R, ϕ, hx, and l, as shown in Fig.
Besides, x can be expressed with variables θ, rs, R, and φ, as shown in the latter Eq. (
Based on the above physical model, the liquid–air interface area formed by the rotation of the arc on a post is:
The meniscus area beneath a droplet on cylindrical posts in square array is expressed by
The air volume between a pillar wall and the surrounded liquid–air interface is the integral:
This volume is expressed as
From the above two equations x can be expressed with the four independent variables:
For a droplet on textured surface with selected projection area Atotal, the IFE includes liquid–air, solid–air, and solid–liquid interfacial energy[25]
The IFE expression of a drop with four independent variables, θ, rs, R, and φ, can be obtained by substituting Eq. (
If the calculation results show x = H, it means that the drop has completely infiltrated posts. In this case, composite metastable droplet does not exist, i.e. it has changed to Wenzel state, which is in the unique minimum IFE. The IFE of a Wenzel droplet is expressed by
Energy barriers usually exist for C–W and W–C transition, which are defined as follows.
The energy barrier of C–W transition, EbC, is defined as the IFE difference between a special composite drop with its base radius equal to that of Cassie drop when its infiltration length x equals to pillar height H and the Cassie droplet, namely
Figure
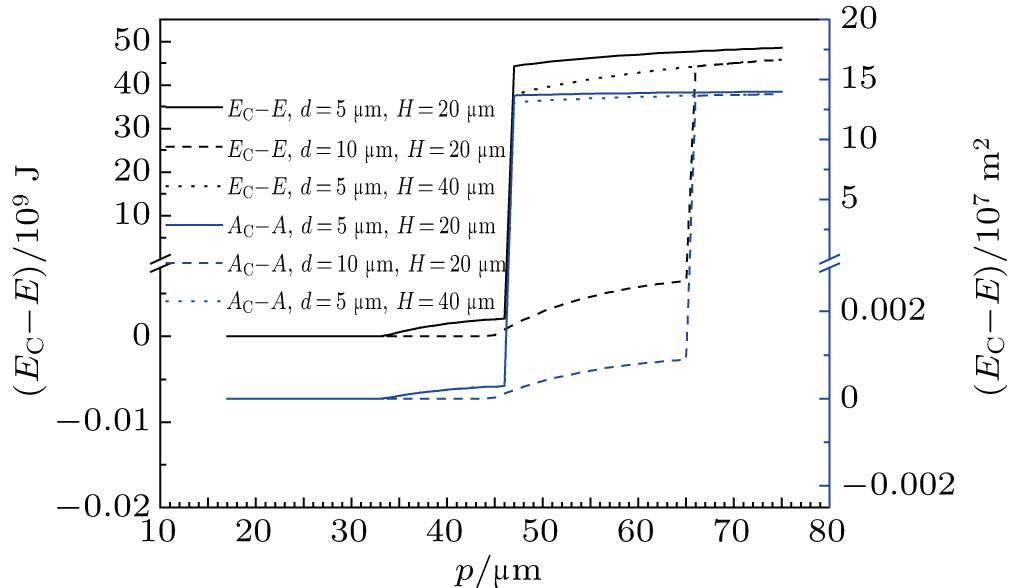 | Fig. 3. (color online) Comparison of IFE and liquid–air area between Cassie and composite droplet with IFE minimum on textured surfaces. V = 2 μL, θ = 110°. |
Besides, it is also clear from Fig.
Above results indicate that the liquid–air interface beneath a composite droplet is a flat one, i.e., a Cassie drop, when pillar pitch is small. But it will become curved when pillar pitch is large.
This model supposed that there is no force acting on the droplet and the interface free energy is the lowest. However, the droplet bottom is always in meniscus when there is driving force acting on the droplet, which is called interface free energy gradient[45] or Laplace pressure in some literatures.[7,15,37,38] But in that case, droplet is not free and the interface free energy is not in the lowest state. Consequently, there is some error between the calculation results of this study and the actual condition.
Figure
Figure
 | Fig. 5. (color online) Parameters of composite droplet with IFE minimum. (a) R and l change with p; (b) x and hx change with p; (C) rs andθ change with p. V = 2 μL, θI = 110°, H = 20 μm. |
The above results show that the meniscus below a composite droplet with minimum IFE includes not only curved part but also a flat one, which is a little different from the model of one complete arc between two posts accepted in several literatures.[5,6,13,17] It should be declared that our model is only valid for droplets without any external force acted and in the locally lowest IFE. When a composite drop is acted by pressure etc, the meniscus beneath it will become a absolute arc, but its IFE is not in minimum state in this case. Therefore the shape parameters of a composite droplet cannot be determined by the method of IFE minimum in this latter situation.
The calculation for composite droplets with IFE minimum also indicates that the angle φ between liquid–air interface and pillar wall constantly equals to π − θI (data not shown). This result illustrates that the wetting state of droplet on pillar side walls accords to the intrinsic contact angle, which is the same as that supposed in literatures.[5,18] Additionally, it is clear from Figs.
Although the liquid–air interface beneath a composite droplet on textured surfaces may be curved, which is different from the plane interface below a Cassie drop, contact angles and base radius of the composite droplet are almost the same as those of Cassie drop, as shown in Fig.
Even though the meniscus of metastable drop does not affect contact angle obviously, it indeed influences the C–W transition especially in the case of short posts which make the meniscus below droplet touch the structural substrate easily.[6,7,25] But the effect of pillar height on C–W transition can not be explained with the flat liquid–air interface beneath Cassie drops.[5–8,25]
The IFE of sessile droplets on textured surfaces was analyzed in this study, and the curvature of meniscus below these drops is small. For instance, the hx in Fig.
In this study, we didn’t consider the force condition of the droplet. Consequently, the calculation result that the contact angle keeps constant is obtained when droplet is in the lowest free energy condition. However, when there is force acting on the droplet the contact angle between micropillar and droplet is constantly changing. In other word, in the actual conditions of C–W transition process contact angle changes from small to large.
The energy barriers of C–W and W–C transitions on different textured surfaces are shown in Fig.
 | Fig. 6. (color online) Energy barriers of C–W and W–C transition change with pillar pitches. V = 2 μL, θI = 110°. Panel (b) is the local amplification of panel (a). |
The effect of drop volume on the energy barriers of C–W and W–C transition is shown in Fig.
 | Fig. 7. (color online) Energy barriers of C–W and W–C transition change with drop volumes. p −d = 20 μm, θI = 110°. Panels (a) and (c) are the local amplifications of panel (b). |
By comparing the two necessary conditions of C–W transition, the above C–W energy barrier being zero and the early x = H condition, it can be seen that both are completely consistent. Therefore, both of them can be used to calculate the C–W transition. It can be said that the basic reason for C–W transition of a metastable drop on textured surface is the disappearing of its local IFE minimum value, or the vanishing of C–W energy barrier. The C–W transition may be inhibited by proper control of the patterns of structures and surface chemical characters, such as by increasing the roughness of pillar sides,[47,48] manufacturing two-tier structures,[17,43,49,50] and raising the intrinsic contact angle of surface materials.[49] The mechanism proposed here for C–W transition can be used to explain and predict the phenomenon of wetting state transformation during droplet evaporation.
It is necessary to further mention that the droplet apparent contact angles were supposed to be unchanging for the calculation of C–W transition energy barrier in almost all published models.[25,30,32,43] We considered, however, this assumption may result in obvious errors when droplet is small or when the droplet volume entering into structures can not be ignored. And the influence of drop volume inside textures on C–W energy barrier was considered in this study as shown from Eqs. (
The work needed to drive the three phase contact line (TPCL) moving along pillar walls beneath droplets was also regarded as a part of C–W energy barrier in the calculations of Bormashenko et al.’s.[44] But we consider that energy barrier is a kind of state function since IFE is a state function and the enerby barrier here is the IFE difference between two droplets with different wetting states, not relevant to the path of droplet TPCL moving along pillar walls. This is just similar to the energy barrier between valley and peak. The barrier in this case only depends on the potential difference between the two locations, but not relevant to the pathways how to climb from valley to mountain top. Indeed however, the wetting work W to overcome the resistance of TPCL moving along pillar wall during C–W transition should be considered to determine the necessary and sufficient condition of the conversion. For textured surfaces with high posts, this condition is:
The W in Eq. (
Then equation (
There are two types of reported experiments to investigate droplets C–W transition on rough surfaces. One of them is to monitor the changes of contact angles of fixed volume droplets deposited on surfaces with different textured parameters. And the C–W transition could be reflected by the sudden change of contact angles. The second way is to identify the abrupt deviation of shape parameters of a droplet during its evaporation on a rough surface. The experimental results from literatures and the corresponding calculation results with this model are compared in Fig.
 | Fig. 8. (color online) Changes of contact angle and IFE barrier Eb plus wetting work of sessile droplets before and after C–W translation on different textured surfaces. (a) experimental data originate from literature,[35]H = 10 μm when d = 5 μm, H = 30 μm when d = 14 μm; V = 5 μL, θI = 109°, θA = 109°; (b)–(d): experimental data originate from literature,[25]V = 3 μL, θI = 110°, θA = 116°, (b) d = 10 μm, H = 40 μm, (c) p = 50 μm, H = 20 μm, (d) H = 2 × d; (e) experimental data originate from literature,[16]V = 4.3 μL, θI = 107.5°, θA = 107.5°. |
As shown in Fig.
It is commonly considered that the C–W transition is limited by IFE energy barrier.[5,19,25,28,43,44] Once this energy barrier diminishes to zero, the C–W transition should take place.[7] However, the droplet C–W transition usually dose not happen even when the energy barrier is zero, but regularly takes place when energy barrier is evidently lower than zero.[25] The main reason for this is that energy barrier is a state function, which merely depends on the IFE difference of droplet between two states.[25] But the C–W transition on the other hand relies on the process path, namely it is related to the process of TPCL moving along structural side walls.[44] Therefore, it is essential to consider not only the energy barrier but also the process work so that the C–W transition can be appropriately determined. The necessary and sufficient condition of C–W transition we developed in Eq. (
While a Cassie state droplet evaporates on a rough surface, the energy barrier plus work declines continuously as the drop size reduces. As a result, the droplet will change into Wenzel state at a certain time when the energy barrier plus work becomes zero. It can be seen from Fig.
 | Fig. 9. (color online) Changes of base area and IFE barrier Eb plus wetting work of a droplet before and after its C–W translation during evaporation. Experimental data originate from literature.[7]d = 3 μm, p = 20 μm, H = 4.8 μm, θA = 116°. Note: the droplet volume required in model calculation was solved by using the measured droplet base area and receding contact angle. |
Finally as shown in Fig.
 | Fig. 10. (color online) Changes of contact angles before and after C–W transition of droplets during evaporation. Experimental data originate from literature,[35]θI = 109°, θA = 109°. (a) d = 5 μm, H = 10 μm; (b) d = 14 μm, H = 30 μm. Note: the droplet volume required in model calculation was solved by using the measured droplet radius and contact angle. |
Line tension[51] is the free energy on unit TPCL. And the free energy of a droplet induced by line tension is the product of line tension and the total length of the TPCL at the bottom of the droplet. However, the IFE mentioned above is only limited to the free energy resulting from interfacial tension, which equals to the product of surface energy and the relative phase-contacted area. When a composite droplet sits on the solid surface with nanostructures the length value of the TPCL beneath the drop may be much larger than the value of contact area. Therefore, even though the line tension is usually obviously smaller than surface tension or surface free energy, the free energy induced by line tension still cannot be ignored.
In this model, the line tension induced free energy is not included. However, the calculation of energy barrier during C–W transition is not influenced since only the cylindrical micro/nanostructure is considered. Consequently, the TPCL length of the droplet bottom is constant during the C–W transition, and the free energy induced by line tension is also unchanged. Therefore the energy barrier of C–W transition (Eq. (
Both free energy and force balance methods can be used to analyse the C–W transition. We had applied the force analysis method[45] to develop a physical and mathematical model for the process judgement of the C–W transition. In that study, the interface free energy gradient was proposed as the driving force of C–W spontaneous transition. And the wetting force or capillary force on the TPCL on a hydrophobic surface was taken as the resistance preventing the TPCL depinning. Compared with the two calculation results of the force analysis and the present free energy method, they are almost the same. Therefore, the two methods are consistent with each other to analyze the C–W transition.
The liquid–air interface beneath a composite droplet in metastable state is either flat or curved on textured surfaces depending on the pitches between posts. The interface is in a plane shape when the pitches are relatively small, but in a curved mensicus when the pitches are comparatively large. The angle between the interface and pillar wall is the same as the supplementary angle of intrinsic contact angle. But the apparent contact angle and base radius of droplet are almost equal to the calculation according to Cassie–Baxter equation. The necessary and sufficient condition of C–W transition is the energy barrier plus wetting work of pillar walls beneath a droplet less than zero for textured surfaces with high posts, or the curved depth of meniscus greater than or equal to pillar height for structural surfaces with short posts.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] |



