Project supported by the National Natural Science Foundation of China (Grant Nos. 11474345 and 11674043).
Project supported by the National Natural Science Foundation of China (Grant Nos. 11474345 and 11674043).
† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11474345 and 11674043).
Electrorheological (ER) fluid is a type of smart fluid whose shear yield stress relies on the external electrical field strength. The transition of ER fluid microstructure driven by the electrical field is the reason why viscosity changes. Experimentally, the transparent electrodes are used to investigate the column size distribution where an external electric field is applied to a colloidal suspension, i.e., ER fluid is increased. The coarsening profile of ER suspensions is strongly related to electrical field strength, but it is insensitive to particle size. In addition, in a low field range the shear stress corresponding to the mean column diameter is studied and they are found to satisfy a power law. However, this dependence is invalid when the field strength surpasses a threshold value.
The electrorheological (ER) fluid, a kind of typical colloidal suspension, is usually composed of high dielectric constant solid particles uniformly dispersed in a low dielectric constant insulating oil. The common ER fluid’s dispersants are silicone oil and mineral oil. Since ER fluid was discovered, researchers have tried to search for a variety of materials as ER fluid’s dispersed phases, for example, aluminum powder, starch, silicon, titanium dioxide, semiconductors, etc. The properties of dispersed phases determine the performance of the ER effect.[1] Wen et al. used nanoparticles (BaTiO(C2O4)2 ·NH2CONH2) coated with urea as the dispersed phase and thus created the first kind of giant electrorheological (GER) fluid. The solid state can reach a yield stress of 130 kPa, which breaks the theoretical upper bound on conventional ER static yield stress.[2] Lu et al. reported that the polar molecules dominated the electrorheological (PM-ER) effect and developed a new PM-ER fluid whose yield stress can reach the order of MPa.[3] The ER effect is reversibly changed in the apparent viscosity of a colloidal fluid under an external electric field. A typical ER fluid consists of solid dielectric particles dispersed in an insulating fluid. It is generally believed that the large increase in the viscosity of ER fluid is caused by field-induced dipole–dipole interactions among the particles.[1,4,8] Previous studies have shown that the rheological response of ER fluid is related to structural changes when the electrical field strength is increased.[9,10]
Many studies have been conducted on the structural formation of ER fluid and computer simulation on the structural formation has been performed.[11] The relationship between the ER fluid microscopic structure and its mechanical and optical properties has aroused considerable interest in the last decade, particularly in relation to the magnetorheological (MR) fluid. The reflection coefficients of TiO3-coated Kaolinite and Y-doped BaTiO3 based ER fluids increased with electrical field strength increasing, which is due to the change of ER fluid structure.[12] Theoretical computation has provided the basis for modeling the analysis of structural evolutions under rapidly increasing external magnetic fields. Results have shown that columns and wall-like structures are formed parallelly to the field direction.[13,14] Wu et al. studied the influence of the particle size on the rheological property of magnetic fluid both in experiment and in computer simulation.[15] Further work has investigated the pattern formation of these structures with the effect of the system particle volume fraction.[16] The dynamic response of the MR fluid to rotating magnetic fields has been a hot research area. Experiments revealed that the magnetic particles preferred to form isotropic clusters and isolated particles appeared, which are governed by the Mason number (the ratio of viscosity to magnetic force).[17] The time-dependent cluster–cluster aggregations of superparamagnetic particles were also analyzed to investigate the characteristics of cluster dynamics.[18] Similar studies have been conducted on the ER fluid. Kittipoomwong et al. investigated the evolutions of both the rheological properties and the suspension structure, and the transient response of electrorheological suspensions in shear flow subjected to a suddenly imposed electric field experimentally.[19] The response of shear stress of ER suspensions to the electric field has been studied theoretically.[20] The kinetics of structural formation in ER suspensions has been investigated using microchannel and high-speed microscopic imaging, showing that the nonuniform growth of the particle structures in the channel was correlated to field strength and flow rate.[21]
Wen et al. experimentally observed the dynamic process of chain and column formations as a function of time under the influence of a high-speed switch power supply.[22,23] Wen et al. found that once the time of field strength applied to ER fluid surpasses a certain time length, the particles first form chains, and these chains then coarsen and eventually form columns spanning between two electrodes. Although we have observed the chain and column profiles earlier and analyzed the structures, mechanisms and dynamics of ER fluid,[24,25] a direct observation of the size distribution of column diameters has not been reported to date.
In this work, an experimental approach to using transparent electrodes to study the column distribution issue is reported. We present the experimental evidence of the particle aggregating processes as a function of field strength. Our findings in the present study are as follows. The size distributions of columns are found to be dependent on the field strength applied to the ER fluid, but independent of the particle size. Under a low electrical field strength, the interaction among particles increases exponentially as a function of the column diameter, which does not occur under high field strength. The column diameter is saturated when the field strength surpasses a critical value. The interaction among particles, nevertheless, is not saturated even though the column size remains unchanged. At a fixed field strength, the columns are very stable and no obvious change is observed as time passes by.
Two kinds of ER fluid cells were used to observe the process of column formation. For a top view of the column shape, ER fluid containing the particle/liquid mixture was sandwiched between two indium–tin oxide (ITO) glasses. The two transparent electrodes with a spacing of 2 mm were connected to a high voltage power supply. For the side view, two parallel brass electrodes were mounted on a glass slide to form a cell with a volume of about 125 mm3 (2.5 mm×10 mm×5 mm). An optical microscope with a video recorder was used to monitor the process of column formation as the field strength was increased. The images were taken after the columns had been stabilized. Glass microspheres respectively with diameters of 0.5 μm and 47 μm are used in this work. These solid particles were dispersed in silicone oil with a volume fraction of 0.15.±0.02. The strength of the shear stress of the ER fluid versus field strength was measured by a rotational viscometer at a fixed shear rate (shear rate: 12 s−1). A rotating inner bob and a stationary outer cup were used with a high power supply. The spacing between the bob and cup was 1.5 mm. All experiments were performed at room temperature.
The column formation from the top and the side with 0.5-μm glass microspheres dispersed in silicone oil are shown in Fig.
| Table 1.
Statistical data of Figs. |
To investigate the size distribution profiles of columns at different electrical field strengths, the number of columns is counted and the diameter of each column is measured. It is very difficult to measure the column diameter, due to the irregular shapes of the columns and because the clusters are connected as observed from the top view. In our measurements the diameter of each column is obtained by averaging the sizes measured along the longest and shortest axes of column. More precisely, as the column has clear contrast to the background, we use software (Photoshop, Adobe; ImageJ, National Institutes of Health; NIS-Element, Nikon) to analyse the pictures thus to distinguish the columns and compute the volumes. The software could outline the profiles and columns and count the number. The diameter of the largest circumscribed circle of column profile is defined as the diameter of this column, which is shown in Figs.
Figure
Following Ref. [17], the mean diameter of column Sd as a function of electric field strength,
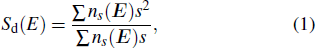 |
 |
Figure
The same aggregating phenomenon can be observed by replacing 0.5 μm microspheres with 47 μm ones as demonstrated in Fig.
Figure
In conclusion, we have demonstrated experimentally that column ripening is strongly related to the force induced by the dipole-dipole interaction among dielectric particles in ER fluid. It is found that under a high field strength, there exists a critical column diameter that is not affected by the particle size. In addition, under a low field strength, the shear stress of the ER fluid increases and the mean column diameter becomes larger. This is not the case when the field strength surpasses a threshold value.
The size distribution of columns in ER fluid strongly depends on the electrical field strength applied to the ER fluid, but the diameter of the column is not sensitive to the particle size. We observe that the interaction among particles increases exponentially as a function of column diameter when the ER fluid is under a low field strength. This is not the case when the electrical field strength is high. In addition, we find that the column diameter will be saturated when the field strength surpasses a critical value. The interaction among the particles, nevertheless, cannot be saturated even though the column size remains unchanged. For the future study, we will try other kinds of ER suspension dispersants and dispersed phases to investigate their microstructure transitions driven by the electric field. We will further analyze the effects of other external conditions on structural transition, such as temperature, volume fraction, etc.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] |






