Project supported by the National Natural Science Foundation of China (Grant Nos. 11747168, 11604246, and 11704007), the Natural Science Foundation of Guizhou Provincial Education Department, China (Grant Nos. KY[2015]384, KY[2015]446, and KY[2017]053), the Natural Science Foundation of Guizhou Provincial Science and Technology Agency (Grant Nos. LH[2015]7232 and LH[2015]7228), and the Science Research Foundation of Tongren University, China (Grant No. trxyDH1529).
Project supported by the National Natural Science Foundation of China (Grant Nos. 11747168, 11604246, and 11704007), the Natural Science Foundation of Guizhou Provincial Education Department, China (Grant Nos. KY[2015]384, KY[2015]446, and KY[2017]053), the Natural Science Foundation of Guizhou Provincial Science and Technology Agency (Grant Nos. LH[2015]7232 and LH[2015]7228), and the Science Research Foundation of Tongren University, China (Grant No. trxyDH1529).
† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11747168, 11604246, and 11704007), the Natural Science Foundation of Guizhou Provincial Education Department, China (Grant Nos. KY[2015]384, KY[2015]446, and KY[2017]053), the Natural Science Foundation of Guizhou Provincial Science and Technology Agency (Grant Nos. LH[2015]7232 and LH[2015]7228), and the Science Research Foundation of Tongren University, China (Grant No. trxyDH1529).
Based on density functional theory, we investigate the electronic and magnetic properties of semi-hydrogenated, fully hydrogenated monolayer and bilayer MoN2. We find that the AB stacking bilayer MoN2 exhibits ferromagnetic coupling of intralayer and antiferromagnetic coupling of interlayer, however, the ground states of the semi-hydrogenated, fully hydrogenated monolayer and AA stcaking bilayer MoN2 are nonmagnetic. The fully hydrogenated system has a quasi-direct band-gap of 2.5 eV, which has potential applications in light-emitting diode and photovoltaics. The AB stacking bilayer MoN2 shows the Dirac cone at K point in BZ around Fermi energy. Furthermore, the interlayer of the AB stacking bilayer MoN2 is subjected to a weak van der Waals force, while the interlayer of the AA stacking forms N-N covalent bond.
Very recently, the nanoscience and emerging nanotechnologies have been dominated by the honeycomb carbon structures in different dimensionalities, such as fullerenes, single (multiwalled) carbon nanotubes, graphene and its ribbons. In particular, graphene with two-dimensional (2D) honeycomb structure is one of the most intriguing carbon structures, in which sp2 hybridized electrons (σ electrons) form a honeycomb structure and the remaining pz (π) electrons follow the massless Dirac (Weyl) equation.[1–4] The energy bands show the linear dispersion (Dirac cone) at the Fermi level (EF) at particular symmetry points, K and K′, in the Brillouin zone (BZ).[5] This gives rises to unique phenomena such as the anomalous quantum Hall effect and unexpected magnetic ordering,[6] which make graphene a promising material used for the next-generation nanodevices.[7] However, graphene with flat surfaces is nonmagnetic, which has limited their potential applications in spintronics. Until now, obtaining the ordered spin structures in 2D materials that exist in ambient conditions is a great challenge.
Recently, transition-metal dinitrides (TMDNs) with rhombohedral MoS2 structure have been experimentally synthesized,[8] where Mo layer is sandwiched between two sulfur layers by covalent forces. Radisavlijevic et al. have demonstrated that it exhibits high on-off current ratio and good electrical performance, which may be used in the future electronic circuits requiring low stand-by power.[9] The strong emission inherited from the direct gap structure of monolayer MoS2 also promises the applications in optoelectronics.
The chemical functionalization is an effective way to tailor the electronic structures of nanostructures. Hydrogen is lowly electronegative and can be used as a functionalization group in nanostructures, such as graphene, germanene, silicon carbide, and boron nitride.[10–13] Recently, the studies of the two-dimensional fully functionalized and semifunctionalized sheets have aroused lots of interest of all.[14–16] However, the influence of the hydrogen-functionalization on the MoN2 sheet has not been mentioned yet. Thus, we focus our attention on the MoN2 sheet functionalized with hydrogen. In this work, we present a systematic investigation on the electronic and magnetic properties of semihydrogenated (MoN2–H), fully hydrogenated (H–MoN2–H) monolayer and bilayer MoN2 sheets.
Density functional theory (DFT) calculations were carried out by using the projector augmented wave method and the generalized gradient approximation (GGA), as implemented in the Vienna ab initio simulation package (VASP).[17–19] The exchange–correlation functional, vdW-DF, which is capable of treating the van der Waals (vdW) force,was adopted (optB86-vdW functional).[20–22] The projector augmented wave pseudopotential with an energy cutoff of 400 eV for the plane-wave basis sets was adopted, and Gamma-centered 15 × 15 × 1 Monkhorst–Pack k-point meshes were used for slab calculations.[23,24] The convergence criteria were set to be 1 × 10−5 eV for total energy and 0.005 eV·Å−1 for Hellman-Feynman force, respectively. A vacuum region of 25 Å was applied in the z direction, which is large enough to make the interaction between neighboring images negligible. Ab initio molecular dynamics simulations with canonical ensemble (NVT) at the temperatures of 300 K and 600 K are performed in 3 ps, respectively. A supercell containing 4 × 4 unitcells is adopted as the model.
The bulk 3R-MoN2 belongs to a rhombohedral R3m space group and has a layered structure. The interaction between the MoN2 layers is weak van der Waals force, with small exfoliation energy; hence it has been proposed that the monolayer MoN2 can be exfoliated using similar methods to those for other 2D materials. As shown in Fig.
We firstly discuss the results of hydrogenated MoN2 sheet (H–MoN2–H), which is similar to its carbon counterpart, graphene, as shown in Fig.
In H–MoN2–H configuration, we find that the system has a nomagnetic moment for each atom. The band structure is plotted in Fig.
 | Fig. 4. (color online) Calculated imaginary part of the dielectric function of H–MoN2–H with (red solid line) and without (black solid line) excitonic effects. |
As stated in previous discussion, the hydrogenation of MoN2 sheet is an exothermic process. Once fully hydrogenated, H can bind on N site with a bond length of 1.02 Å for the corresponding N–H dimer in free state. Now the next question is starting from the fully hydrogenated MoN2 sheet. Can one find a way to remove hydrogen from one side forming a semihydrogenated MoN2 sheet? If so, how will the properties change?
Like the graphene sheet, all the N sites are equivalent. Thus, when removing half of H atoms from a fully hydrogenated MoN2 sheet, we have only one option for the semihydrogenated sheet as shown in Fig.
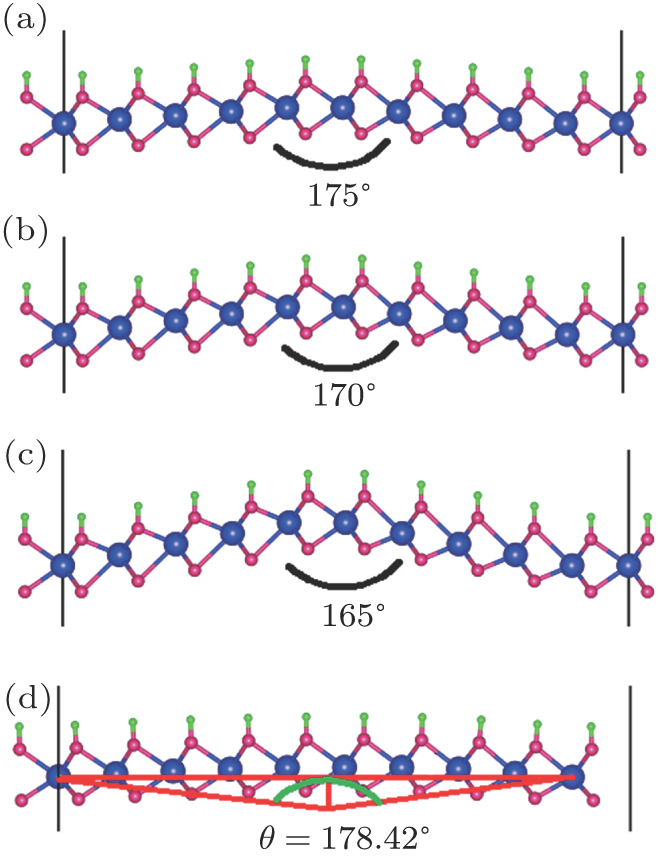
The semihydrogenated monolayers are asymmetric in the normal direction, therefore, it should be subjected to spontaneous bending. In order to estimate its intrinsic curvature, we calculate three bending structures as shown in Figs.
We now turn to the magnetic and electronic structure of bilayer MoN2 sheet [Fig.
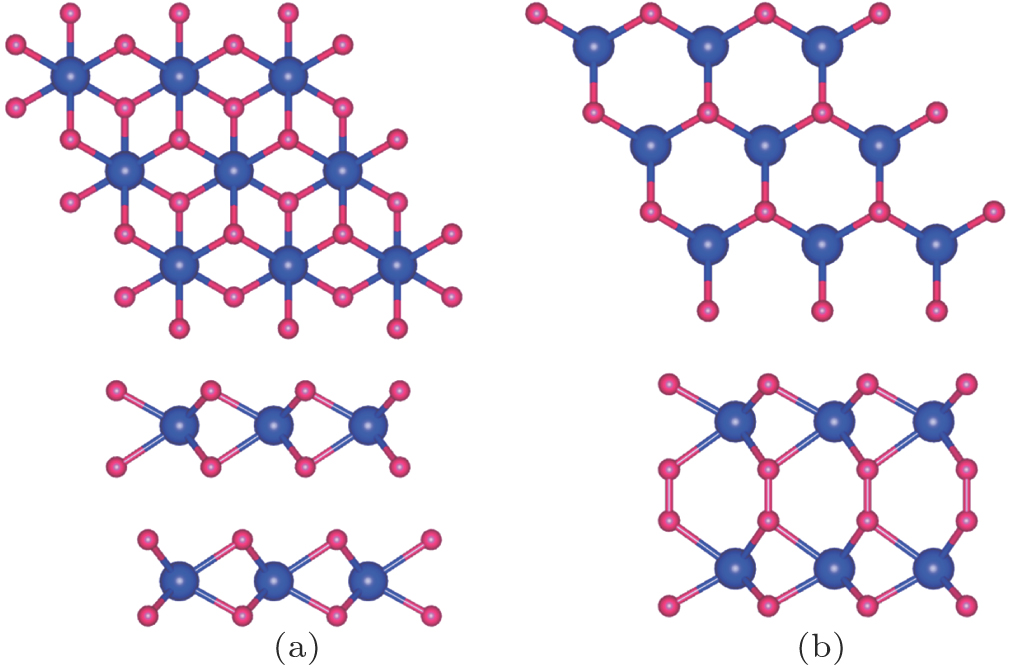 | Fig. 6. (color online) (a) AB stacking bilayer MoN2 (2 × 2 supercell) and (b) AA stacking bilayer MoN2 (2 × 2 supercell). Mo and N atoms are in blue and red, respectively. |
 | Fig. 7. (color online) Structure snapshots of ((a) and (b)) AA and ((c) and (d)) AB stacking MoN2 for MD simulation at 300 K and 600 K. |
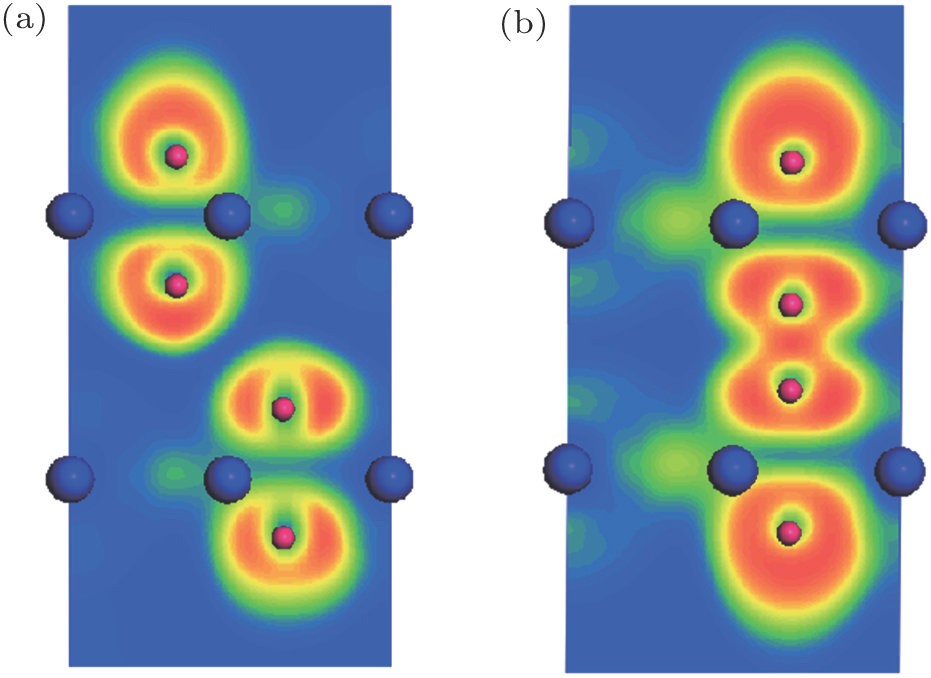
In the AA stacking bilayer MoN2 system, the interlayer coupling is nonmagnetic as a result of the N atoms bonding. In the AA stacking, dN−N = 1.38 Å, which is less than the typical N–N bond length (∼ 1.45 Å), implying the N–N single bond state. To verify the above schematic, we calculate the electron localization function (ELF) of the stable structures for AB stacking MoN2 and AA stacking MoN2, and the results are shown in Fig.
To find how stacking affects the electronic structure, we calculate the band dispersion for AB stacking and AA stacking as shown in Figs.
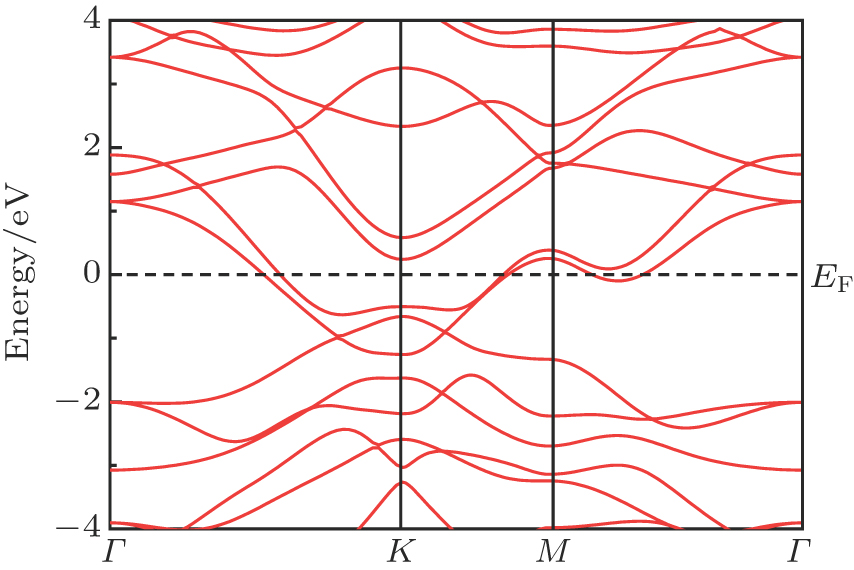 | Fig. 9. (color online) Calculated energy band of the stable structure for the AA stacking MoN2. EF is shown by dashed line. |
In this work, we have systematically investigated the electronic and magnetic properties of semihydrogenated, fully hydrogenated monolayer MoN2 and bilayer MoN2 sheet. The main conclusions are as follows. (i) Our results reveal that the AB stacking bilayer MoN2 exhibits ferromagnetic coupling of intralayer and antiferromagnetic coupling of interlayer, however, the ground states of the semi-hydrogenated, fully hydrogenated monolayer and AA stcaking bilayer MoN2 are nonmagneticthe. (ii) The fully hydrogenated system has quasi-direct band-gap of 2.5 eV, showing that it is very good nanoscale solar cell absorbers. (iii) In bilayer MoN2, the interlayer of the AB stacking bilayer MoN2 is due to weak van der Waals force, while the interlayer of the AA stacking forms N–N covalent bond.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] |