† Corresponding author. E-mail:
A single-image passive ranging and three-dimensional (3D) imaging system with chiral phase encoding was proposed in 2011 [Opt. Lett.
In the past decade, the increasing interest has been aroused in the use of hybrid optical and digital techniques to provide improved imaging capabilities or extra degrees of freedom in designing the imaging systems. This technique which is known as wavefront coding brought great changes to optical system design.[1–3] The wavefront coding system consists of two parts: optical encoding and digital decoding. The system is optically encoded by using a specially designed phase mask on the pupil plane, thus it has particular characteristics such as sensitivity to the object distance.[4] The images captured in the image plane are called encoded images. Desired information such as object distance or sharp graphics information is usually extracted from the encoded images through digital decoding.
Simonov et al. presented a single-image passive ranging and three-dimensional (3D) imaging system in incoherent light based on a wavefront coding technology by using a chiral phase mask in 2011.[4] They analyzed the system in the frequency domain, while in the present paper we present the theoretical analysis in the spatial domain. We deduct the analytic relationships between the object distance and the point spread function, and between the object distance and the encoded image. Then the depth information can be extracted from the encoded images. In addition, the chiral phase mask used in previous research is processed by machine tools. Since the optimal parameter of the phase mask may vary with service time and circumstances, it is beneficial to employ a programmable phase element that can be optimized in real time.[5] Therefore, the phase mask is generated by a spatial light modulator (SLM), which is an object that imposes some form of spatially varying modulation on a light beam and it is programmable in real time. By doing this, we set up a programmable real-time passive ranging system. It is more flexible and can be adjusted in real time.
In Section
The imaging quality of an optical system is determined by the pupil function.[6,7] By adding a chiral phase mask on the pupil plane, the optical system becomes particularly sensitive to the object distance. The object distance reflects the depth information in the object space. The digital decoding is used to extract the depth map from the encoded image. The depth information can be used to restore the 3D image of the object. This paper will analyze the system in the space domain.
Sharp images will be achieved if the system satisfies the Gauss imaging formula. Assume that f is the focal length of the optical system, zi is the image distance, and zo is the object distance. Similarly, the image distance will change 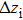
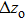
 |
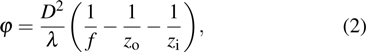 |
It is assumed that a phase mask Z is placed on the pupil plane of the optical system. Then the exit pupil of an optical system can be described in canonical pupil coordinates 
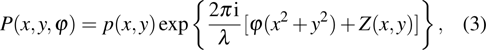 |

 |

 |
The PSF of a wavefront coding optical system using a chiral phase mask is called the encoded PSF. In the case of small φ, it can be approximated as
 |
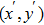
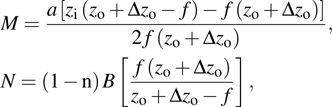 |
According to Eq. (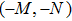

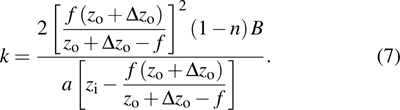 |
However, the image captured in the image plane is regarded as the convolution of the object and PSF. Consequently, in the case of a spatially-extended object, to determine the unknown object distance, the encoded image should be additionally analyzed. We will discuss a method to extract the object distance from the encoded images in the following subsection.
Suppose that I denotes the object. Image 
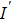
 |
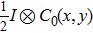
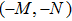
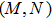
Note that the displacement in space domain corresponds to the phase shift in the frequency domain. Thus the spectrum of the object U0 in the frequency domain is the Fourier transform of the object 
 |
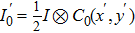
 |
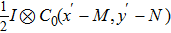
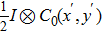
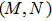

 |

 |
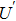
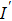
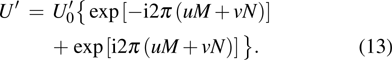 |
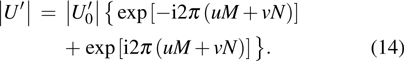 |
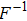

 |
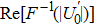
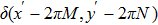
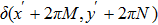

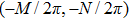
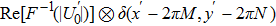
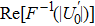
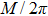
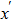
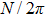

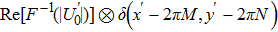
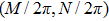
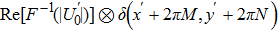
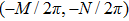

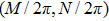
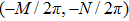
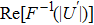
Using this method, we can extract the depth information from the encoded images in the wavefront coding optical system with a chiral phase mask.
An SLM is used to generate the chiral phase instead of a machine-tooled phase mask for its flexibility. The SLM used here is a twisted-nematic liquid-crystal modulator (HEO0017) from Holoeye. The device enables electrically modulated birefringence in transmission mode and is controlled by means of a video signal with a resolution 1024×768 pixels and 8 bits in depth.
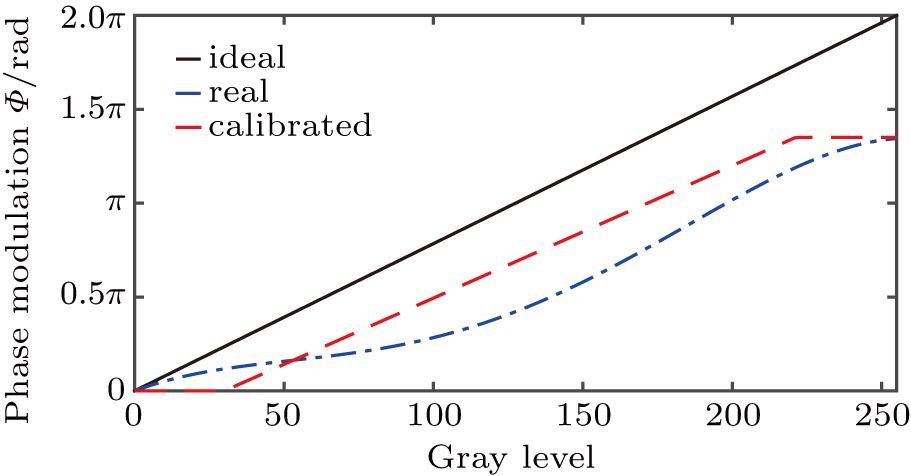
Generally, the SLM needs to be calibrated before use. An interference device is set up to calibrate the SLM. The SLM is placed between a polarizer and an analyzer. As shown in Fig.
To achieve a maximum phase modulation, the optimal combination of angles of the polarizer and the analyzer need to be found out. The angles of the polarizer and analyzer are adjusted by keeping the modulation at half of the SLM in the application of the gray level at 0, while at another half of the SLM the gray level is at 255. The best combination of angles of the polarizer and the analyzer is obtained when the misplacement of interference fringes reaches the maximum.
To obtain the relationship between the gray level and the phase modulation at the optimal combination of angles of the polarizer and the analyzer, the gray level of one half part of the SLM is kept at 0, and another half is linearly varied. The dynamic range for the variation of gray level is [0, 255]. The phase modulation caused by the variation of SLM gray level results in the misplacement of interference fringes. By measuring the misplacement of the interference fringe in the CCD, we obtain the phase modulation
 |
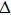
However, the ideal modulation curve is linear and ranges from 0 to 255 as shown by the solid line in Fig.
To verify the rotation effect of the PSF, a PSF test system is set up as shown in Fig. 
The object distance is varied by moving the microscope objective. Figure 

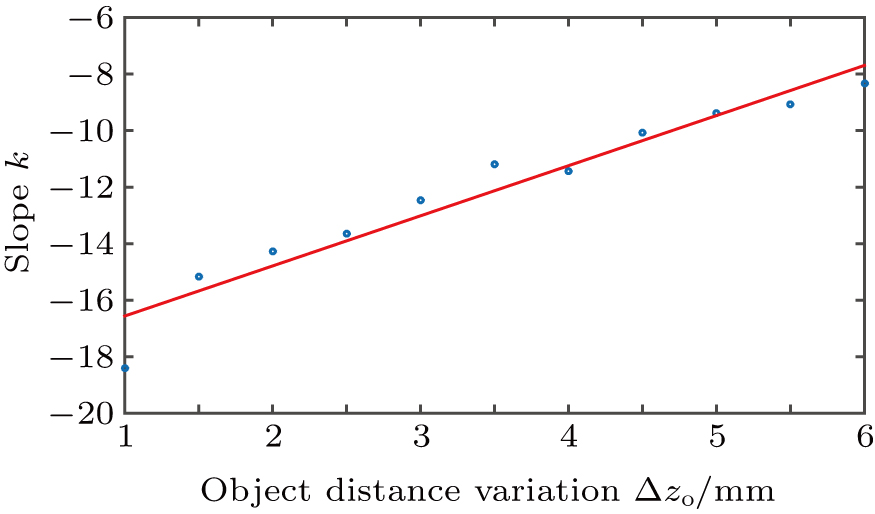 | Fig. 7. (color online) Slope of the line between centers of defocused spots in PSF versus object distance variation. |
Two wooden blocks with step height are used as an object as shown in Fig.
The encoded image is divided into a number of sub-images which will be analyzed to obtain the object distance of each sub-image. All sub-images are then processed separately to determine their local ranges.[4] The encoded image shown in Fig.
 | Fig. 10. (color online) (a) Calculation result of Eq. ( |
According to Fig. 
The system through chiral phase encoding is sensitive to the object distance. In this paper, we deduce the analytic relationships between the object distance and the point spread function, and between the object distance and the encoded image. The theoretical analysis shows that the point spread function has two spots, which will rotate with the variation of the object distance. In addition, the processed spectrum of the encoded image has twin peaks rotating with the variation of the object distance. Then the depth information is extracted from the twin peaks of the encoded image. The theoretical analysis is verified by a wavefront coding system with a chiral phase which is generated by a phase-only liquid-crystal spatial light modulator. Compared with the fixed phase mask, the phase generated by the liquid-crystal spatial light modulator is very flexible and can be adjusted in real time.
The resolution of the 3D image obtained in the experiment can be further increased. The images can be divided into more sub-images to achieve a smooth image. Furthermore, the denoising algorithms will be considered to extract the twin peaks of the encoded image in an easier way in future research. Generally, weakly textured objects are accurate when the spatial spectrum of the object is wide enough to cover at least a few characteristic fringes. The use of high definition phase encoded images can also improve the reconstruction accuracy of the depth map of the object.
In this paper, a passive ranging system is also analyzed from another point of view, and the intuitive relationship between the depth information and the encoded image is presented. It is believed that the present study is helpful in developing the passive 3D imaging technology.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] |