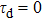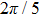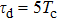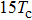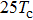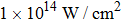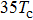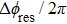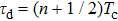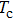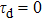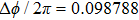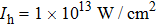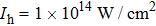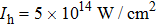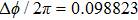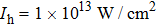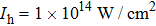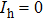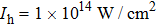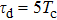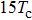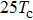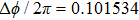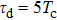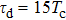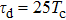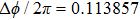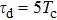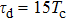† Corresponding author. E-mail:
The frequency-comb structure in the extreme ultraviolet (XUV) and vacuum ultraviolet (VUV) regions can be realized by the high-order harmonic generation (HHG) process driven by frequency-comb fields, providing an alternative approach for the measurement of an unknown frequency in XUV or VUV. We consider the case of two driving frequency-comb fields with the same repetition frequency and the carrier frequencies of fundamental- and third-harmonics, respectively. The many-mode Floquet theorem (MMFT) is employed to provide a nonperturbative and exact treatment of the interaction between a quantum system and the frequency-comb laser fields. Multiphoton transition paths involving both fundamental- and third-harmonic photons are opened due to the coupling of the third-harmonic frequency-comb field. The multiphoton transition paths are superpositioned when the carrier-envelope-phase shifts (CEPs) fulfill the matching condition. And the interference of the multiphoton transition paths can be controlled by tuning the relative envelope delay between the fields. We find that the quasienergy structure, as well as the multiphoton resonant high-order harmonic generation (HHG) spectra, driven by the two frequency-comb fields can be coherently controlled via the interference of multiphoton transition paths. It is also found that the spectral intensities of the generated harmonics can be modulated, and the modulation behavior is harmonic-sensitive.
In the past two decades, high-order harmonic generation (HHG) from the interaction between matter and intense laser fields has been proposed as an alternative method to obtain coherent light sources in the extreme ultraviolet (XUV) and vacuum ultraviolet (VUV) regions.[1–4] Besides the fundamental physics of the laser–matter interaction, the manipulate of the features of the generated spectra has also drown researchers’ attention due to potential applications.[5–10] When the matter–laser interaction is driven by a train of identical laser pulses with a fixed time interval, which corresponds to a frequency-comb structure in the frequency-domain, the frequency-comb structure is preserved in the harmonics in the HHG spectrum.[11–14] It provides an approach to bring the frequency-comb structure into XUV and VUV regions, which will allow the measurement of an unknown frequency in XUV or VUV owing to the precise and direct link between known and unknown frequencies. The generation of XUV and VUV frequency comb spectroscopy has led to the advancements in development of optical atomic clock,[15–20] high-precision optical frequency spectroscopy,[21–28] and test of quantum electrodynamics.[14,29–31]
It has been theoretically proved that HHG driven by a frequency-comb field can be dramatically enhanced via multiphoton resonance by tuning the carrier-envelope phase (CEP) shift of the driving field.[32,33] The employment of different color laser pulses has also been proved to be one of the schemes to enhance the intensities of the HHG spectra.[34–48] And the spectra can be modulated by tuning the relative envelope delay τd and/or the relative phase between pulses φ. For the case of two multiple-cycle pulses, the modulation features of the spectra by tuning τd are similar to those by tuning φ. When two trains of pulses are employed, the modulation features of the spectra by tuning τd may be different from those by tuning φ. Recently, a two-level system driven by intense fundamental- and weak second-harmonic frequency-comb fields was investigated in Ref. [49]. It was shown that the frequency-comb HHG spectra can be enhanced via constructively interference between the multiphoton transition paths.
In this paper, we theoretically investigate the coherent control of the quasienergy structure and multiphoton resonant high-order harmonic generation (HHG) driven by two frequency-comb fields. Additional multiphoton transition paths involving photons from both fields are opened, and the coherent control is achieved via interference of the multiphoton transition paths by tuning the relative envelope delay between the fields. We consider the case of two frequency-comb fields with the same repetition frequency and the carrier frequencies of fundamental- and third-harmonics, respectively. When the CEP shifts of the two fields are matched, different multiphoton transition paths can interfere with each other. Our calculation indicates that the quasienergy structure of the driven system can be modulated by tuning the relative envelope delay. Meanwhile, the spectral intensities of the generated harmonics can be modulated, and the modulation behavior is harmonic-dependent, and related to the multiphoton transition paths that contribute to the spectrum.
The paper is organized as follows. We present the many-mode Floquet theorem (MMFT) for the treatment of the interaction between quantum systems and two frequency-comb laser fields with different carrier frequencies and the same repetition frequency in Section
For a quantum system driven by laser fields, the time-dependent Schrödinger equation can be written as
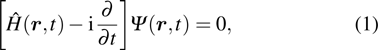 |
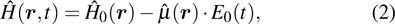 |
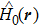
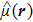
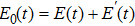
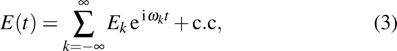 |
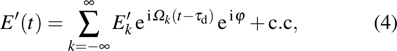 |
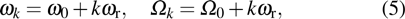 |
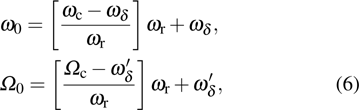 |
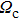

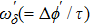

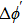
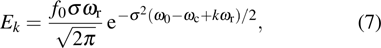 |
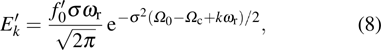 |

The time-dependent Schrödinger equation with Hamiltonian (
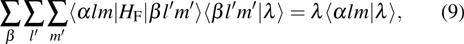 |
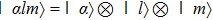
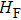
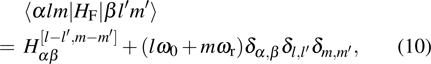 |
 |
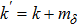
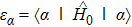
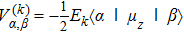
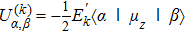
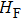
Solving the matrix eigenvalue problem (
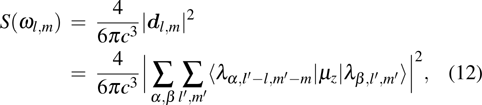 |
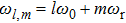
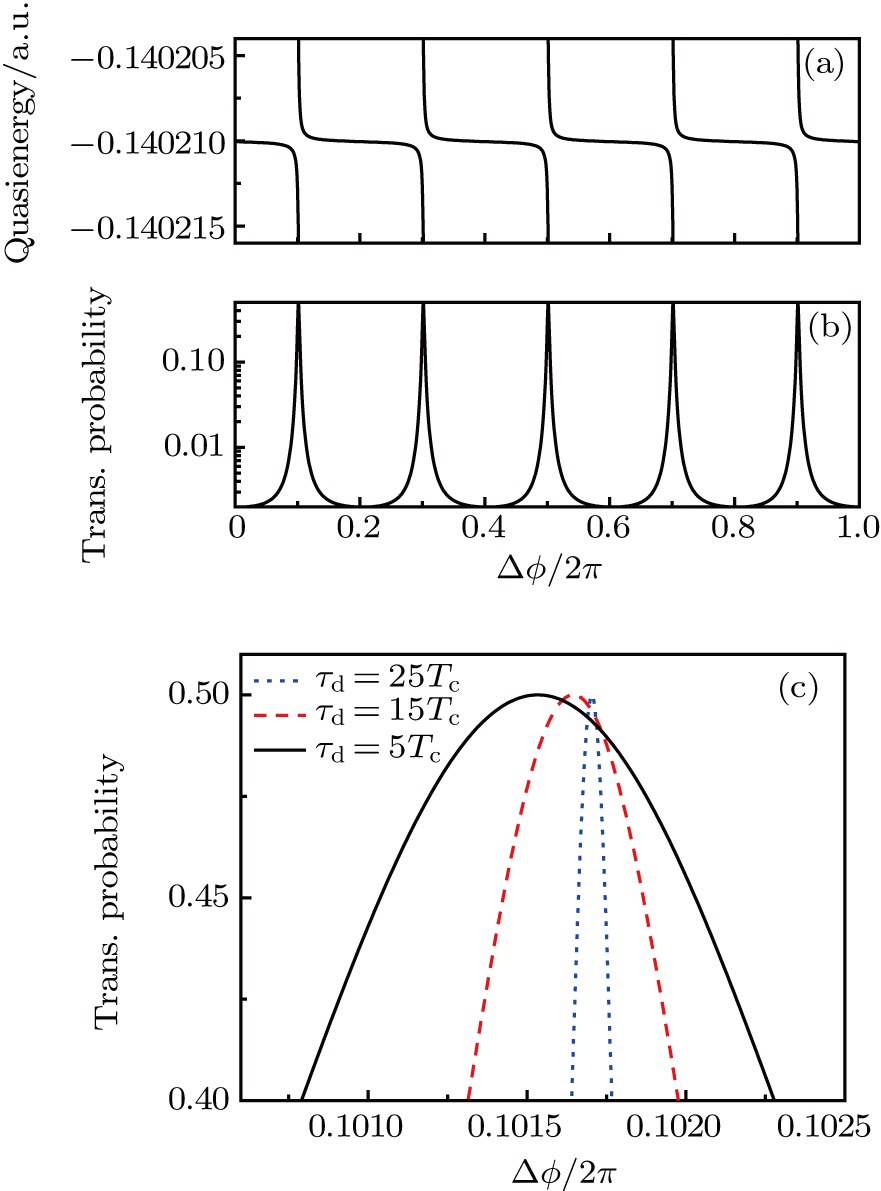
In this section, we present a case study of the modulation of quasienergy structures and HHG power spectra generated from a two-level system driven by fundamental- and third-harmonic frequency-comb laser fields by varying the envelope delay. The parameters of the fundamental frequency-comb field are peak intensity 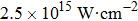
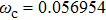
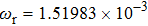
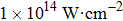
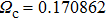
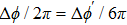
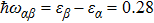
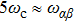

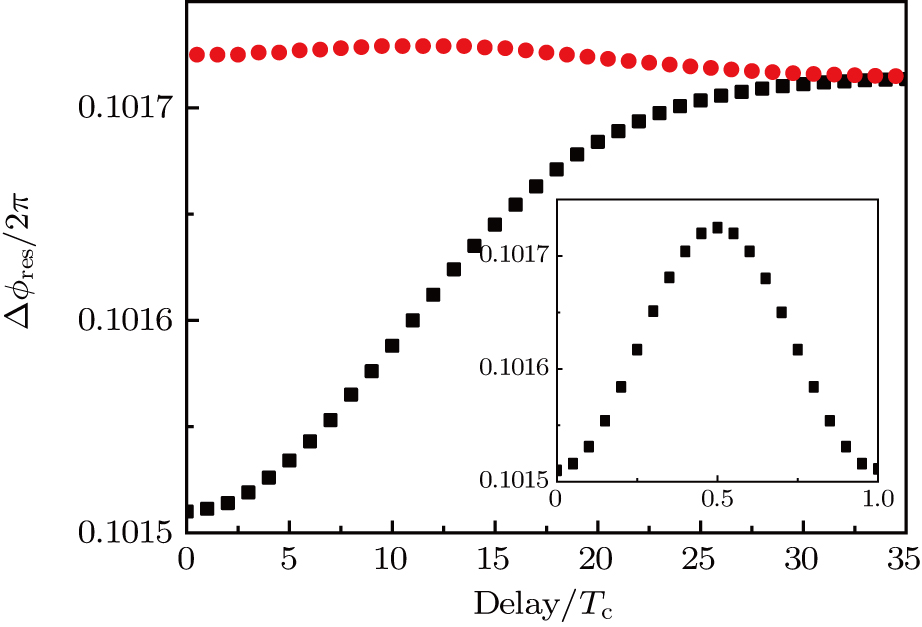
Under the matching condition 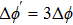

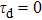
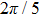
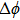
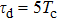
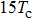
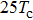
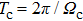
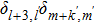
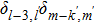
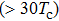
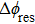
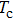
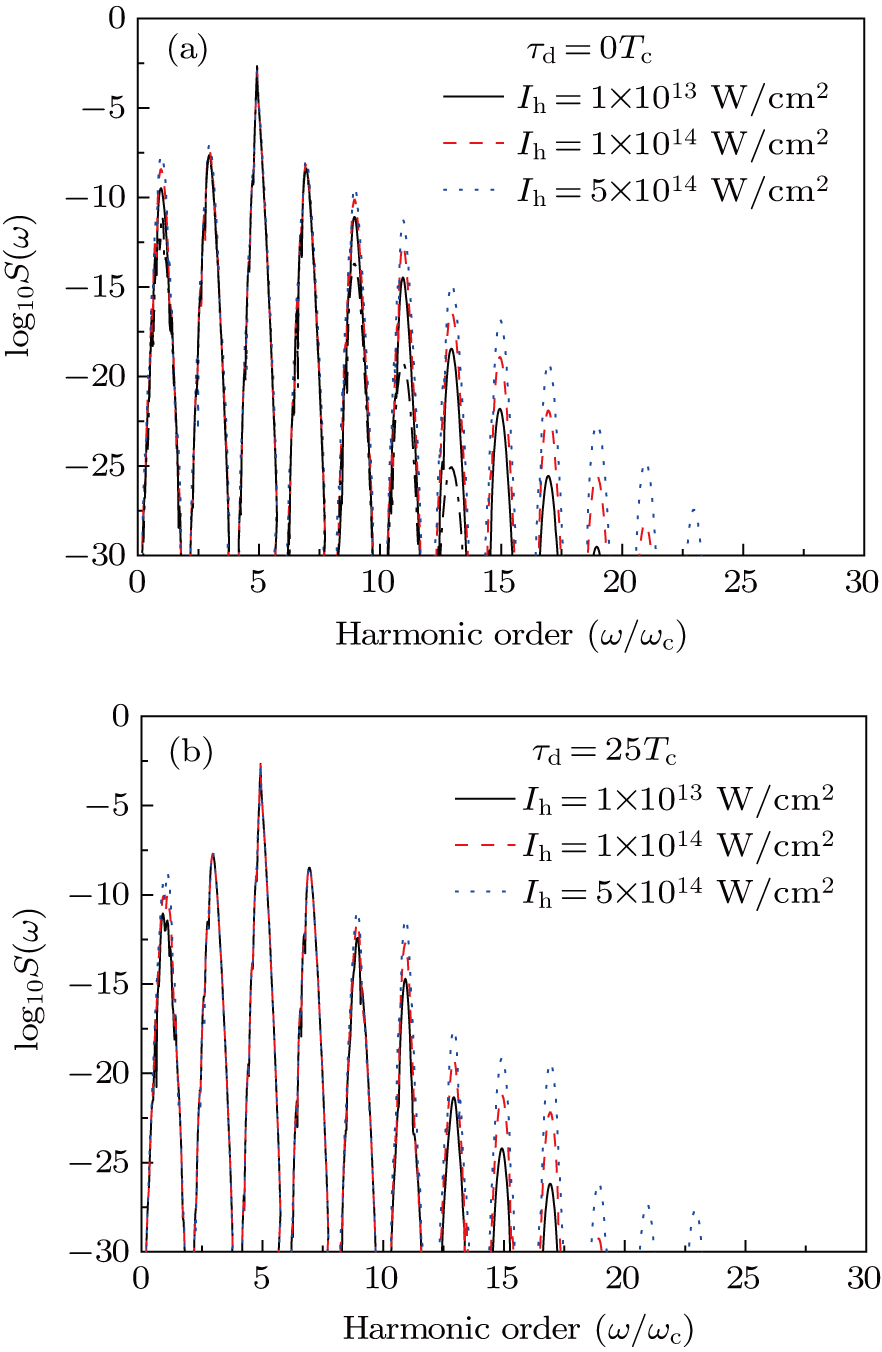
Besides the quasienergy structure, the harmonic spectra can also be modulated by varying the envelope delay. Owing to the coupling of the third-harmonic driving field, additional multiphoton transition paths involving both fundamental- and third-harmonic photons are opened, and they contribute to the HHG power spectra, as shown in Fig. 
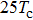
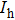
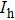
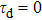
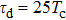
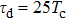
For further investigating the dependence of the spectra on the envelope delay, the HHG power spectra by varying the envelope delays τd with 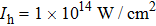
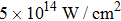
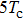
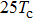
For instance, the 11th harmonic is mainly contributed by three multiphoton-transition paths taking the excited level as the intermediate state, the first one via the absorption of 6 fundamental-harmonic photons, the second one via the absorption of 2 third-harmonic photons, and the third one via the absorption of 3 fundamental-harmonic photons and 1 third-harmonic photon. The first two paths are the main contribution and they are independent of the envelope delay, while the third path is dependent on the envelope delay. The 13th harmonic is also mainly contributed by three paths, the first one via absorption of 8 fundamental-harmonic photons, the second one via the absorption of 5 fundamental-harmonic photons and 1 third-harmonic photon, and the third one via the absorption of 2 fundamental-harmonic photons and 2 third-harmonic photons. However, only the first path is independent of the envelope delay. As a result, the spectral intensities of the 11th and 13th harmonics show different modulation behaviors as varying the envelope delay.
We present a theoretical investigation of the coherent control of the quasienergy structure and HHG power spectra driven by two frequency-comb fields via interference of multiphoton transition paths by tuning the relative envelope delay between the fields. We consider the case of two frequency-comb fields with the same repetition frequency and the carrier frequencies of fundamental- and third-harmonic frequencies. For accurate treatment of the interaction between a quantum system and the frequency-comb fields, the many-mode Floquet theory is employed. Multiphoton transition paths involving both fundamental- and third-harmonic photons are opened, and they can interfere with each other when the CEP shifts satisfy the matching condition. It is found that, not only the HHG power spectra, but also the quasienergy structure of the driven system can be coherently controlled. Our calculation results show that the quasienergies of the driven system can be tuned by varying the relative envelope delay when the pulses of the two fields overlap with each other. Meanwhile, owing to the dependence of the multiphoton transition paths on the relative envelope delay, the spectral intensities of the generated harmonics show different modulation behaviors when varying the relative envelope delay. Note that the effects of ionization and decay of levels, which are not included in this study of closed two-level system, also impact the quasienergy structure. And the study of realistic atomic systems including these effects is in process.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] |