† Corresponding author. E-mail:
In the present work, firstly, a first-principles study of the structural, electronic, and electron transport properties of the HgxMg1−xTe (HMT) ternary compound is performed using the ABINIT package and the results are compared with Cd0.9Zn0.1Te (CZT) as a current room-temperature photodetector. Next, the response functions of Hg0.6Mg0.4Te and Cd0.9Zn0.1Te under electromagnetic irradiation with 0.05 MeV, 0.2 MeV, 0.661 MeV and 1.33 MeV energies are simulated by using the MCNP code. According to these simulations, the Hg0.6Mg0.4Te ternary compound is suggested as a good semiconductor photodetector for use at room temperature.
Semiconductor photodetectors are used to detect electromagnetic radiation. The high resolution and efficiency of semiconductor photodetectors depend on a high atomic number (Z), a small band gap and, finally, a high product value of charge-carrier mobility and free electron–hole lifetime. On the other side, at room temperature (RT), an unwelcome dark current is produced by thermal noises and leakage currents in the photodetector. At RT, the dark current is negligible provided there is high electrical resistivity (

In order to achieve an appropriate option for RT detection comparable to Cd0.9Zn0.1Te, we propose the Hg0.6Mg0.4Te ternary compound. In this research, we investigate this claim by using the computational approach. We study its band gap, electron mobility and response function to the energetic electromagnetic radiation, mechanical properties, and electrical resistivity.
The HgTe binary compound[5] is a semimetal with a narrow and negative band gap, huge spin–orbit coupling (SOC) interaction,[6] high atomic numbers of Hg and Te atoms, and high electron mobility.[7] On the other hand, natural magnesium telluride (MgTe) has a wurtezite structure, but thanks to new material synthesis methods such as molecular beam epitaxy (MBE) and metal-organic chemical vapor deposition (MOCVD), the production of the zinc blende (ZB) structure of MgTe (β-MgTe) is possible. Its band gap is wide and its charge mobility is low.[7] In the present work, we use the ZB phase of the MgTe compound and concentrate it with Hg atoms to simulate the HMT ternary alloy.
Previous research on the HgxMg1−xTe (HMT) ternary compound[8–10] involved density functional theory (DFT) simulations or experimental measurements of the structural and electronic properties of the binary and ternary compounds without charge transport consideration, and indicated that doping of the Hg atoms inside β-MgTe reduces the β-MgTe band gap. The mechanical properties of the II–VI compounds were studied in Refs. [11] and [12]. In the present work, in order to achieve a complete investigate of the feasibility of using the HgxMg1−xTe ternary compound as a good RT photodetector, we study as a first step the structural and electronic properties of the β-MgTe (shortened name, MgTe) and HMT including the band structure, band gap and effective masses of the electron and hole. In the next step, we simulate the optical properties of the HMT including the static dielectric constant, infinite dielectric constant and optical phonons energies. Then we calculate the charge-carrier mobility of the HMT. These calculations give the optimal Hg and Mg atom concentrations in the HMT. With these optimal values, we simulate the response function of the HMT under electromagnetic irradiation. We present the elastic stiffness tensor elements of this optimum compound, which are the major basis of the mechanical properties calculations. Finally, we report the electrical resistivity. We repeat the other DFT calculations[8,9] using generalized gradient approximation (GGA) pseudopotentials in the presence of SOC, in addition to the GW approximation correction.
The rest of the paper is organized as follows. Section
In this work, firstly, the ABINIT[13] package is used to simulate the electronic and transport quantities of compounds and, next, the MCNP[14] package is used to simulate the energetic electromagnetic radiation interactions with matter.
ABINIT as an open source code, works within DFT, using pseudopotentials and a plane-wave basis set. In our DFT calculations,[15,16] the Trouiller–Martins,[17] Perdew–Burke–Ernzerhof,[18] and Hartwigsen–Goedecker–Hutter (HGH)[19] types of the exchange–correlation functional are used. The kinetic energy cut off for the wave functions expansion is optimized at about 30 Hartree. The lattice constants of the HgTe, MgTe and HMT compounds are theoretically estimated by the convergence threshold of total energy less than 0.0001 Hartree. A 
In the present work, according to the acceptable accuracy and speed of calculations, the alchemical mixing of pseudopotentials known as virtual-crystal approximation (VCA) method is used for ternary alloy semiconductor simulations instead of the supercell method. The VCA method is used to transform an ordered structure into a disordered structure within DFT approach calculations. In the VCA, the main idea is to introduce an element whose properties would reflect the properties of the two atoms simultaneously at a given proportion. This approach is simply a linear combination of two one-electron potentials describing pure crystals.
The relativistic norm-conserving pseudopotentials of the ion cores of Hg, Mg and Te can be written as[20]
 |
 |
 |
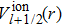
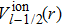

 |
The MCNP is a general-purpose Monte Carlo N-particle code that can be used for neutron, photon, electron or coupled neutron/photon/electron transport using cross-section data. Given some inputs, the MCNP returns the dose, flux, response function, etc. In our calculations, we use ENDF/B-VI interaction cross-sections, a crystal cylindrical geometry with 3.81 cm radius and 7.62 cm height and an electromagnetic radiation point source with 109 incident photon number, 0.05 MeV, 0.2 MeV, 0.661 MeV and 1.33 MeV energies, and 0.01 cm distance to the detector.
The GGA approximation and HGH type pseudopotentials in the presence of SOC interaction are used to obtain the physical quantities of the HgTe and MgTe compounds, which show a good agreement with the experimental values. The obtained results are given in the following sections. This approach is used to calculate the effective mass, static dielectric constant and optical phonon energies; and the more precise approach, the GW approximation, is used to calculate the energy band gap.[13] The orbital structure of the 80Hg atom is [54Xe]4f145d106s2. Since the d orbital is full, the choice of the core and valence electrons is effective to calculate the band structure. To simulate such atoms, the number of valence electrons, 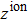
The band structures of the MgTe compound are calculated by both GGA and GW approximation approaches and presented in Figs. 

Figure
 | Fig. 2. The calculated band gap of the HMT as a function of x by GGA (solid triangle) and the GW approach (hollow triangle) in the presence of SOC compared to the MgTe (cross)[7] and CZT[2] experimental values. |
In an electrical circuit, unwelcome thermal noises on the surface of a semiconductor with band gap less than 1.5 eV are seriously produced. On the other hand, the number of photo-produced electron–hole pairs inside a semiconductor with band gap greater than 2 eV is few. Thus the optimum energy band gap for the RT photodetector is about 1.5 eV. According to Fig. 
The underestimating of band gap in DFT using traditional approximations for the exchange–correlation term (such as GGA) is related to the fact that such approaches cannot simultaneously obtain the exchange–correlation energy and its charge derivative accurately.[23] Using the Green function (GW) approach and considering the self-energy contributions, we can overcome this deficiency of the DFT. The improvement is clearly shown in Fig.
According to the obtained result of the previous section, the HgxMg1−xTe ternary compound with 
The most important electronic scattering processes relevant to the charge-carrier mobility in semiconductors include[24–26] deformation potential scattering, piezoelectric phonon scattering, polar optical phonon scattering, ionized impurity scattering, alloy scattering and other electron scattering types.
The total charge-carrier mobility depends on the secondary mobility by the Matthiessen rule[25,26]
 |
 |
 |

 |
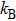
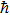
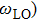



The static dielectric constant and high frequency dielectric constant are related to the transverse and longitudinal modes of the optical phonons by the Lyddane–Sachs–Teller equation[25,26]
 |



 | Fig. 3. (a) Electron effective masses, (b) the static dielectric constant, (c) transverse and (d) longitudinal optical phonons energies of the HMT as a function of x (solids), compared to the experimental values[7] (hollows). |
According to Fig. 
| Table 1.
Simulated and experimental charge-transport quantities of MgTe and HgTe compounds. . |
Figure 
 | Fig. 4. Calculated electron mobility of the HMT at T = 300 K compared to the HgTe, MgTe,[7] and CZT[2] experimental values (hollow). The total mobility is equal to the electron mobility because of the heavy effective mass of a hole relative to that of an electron. |
Based on the obtained results in this section and the previous section, the optimum x value of 0.6 is suggested. In the next section, the response functions of the Hg0.6Mg0.4Te and Cd0.9Zn0.1Te compounds to the energetic electromagnetic radiations are calculated by the MCNP package and compared.
The basis of radiation detection by semiconductor crystals is the production of the free electrons and holes under irradiation of the crystal. The output of the irradiated crystal is an electrical signal described by the response function or pulse height distribution and is collected by electronic systems. The response functions can be calculated by one of three different ways: experimental, Monte Carlo or semi-empirical methods. One of the abilities of the MCNP code is the response function generation by the Monte Carlo method.[22] The photon energy regime in MCNP is from 1 keV to 1 GeV. Since the electromagnetic radiation in the x and gamma regions is used abundantly in industrial, medicine and research fields, we calculate the response function to the energetic electromagnetic radiations for the Hg0.6Mg0.4Te and Cd0.9Zn0.1Te by MCNP in these regions with 0.05 MeV, 0.2 MeV, 0.661 MeV and 1.33 MeV radiation energies. The presented response functions in Fig.
When doping an impurity inside a semiconductor, it is necessary to investigate its mechanical properties.[1] When there is interaction between a native defect and an impurity or between the lattice and an impurity, lattice relaxation occurs locally to minimize the energy. An impurity in a lattice that causes significant lattice relaxation is called the DX-center.
Using the calculated quantities in the previous sections, such as m, 

The elements of this tensor are used to calculate the thermal and mechanical quantities of the materials, such as the Debye temperature, elastic stress tensor, elastic strain tensor, Youngʼs modules, Poissonʼs ratio, bulk modules, shear modulus, isotropy factor, linear compressibility, Cauchy ratio, Born ratio, micro-hardness and sound velocity.[27] We use the following relations to calculate the c11, c12 and c44 elements:[11]
 |
 |
 |

 |
| Table 2.
The elements of the elastic stiffness tensor. . |
As we can see, the c11, c12 and c44 elements of the HgTe and MgTe binaries and Hg0.6Mg0.4Te ternary compounds are approximately equal,[7] which is a favorable condition for the formation of DX-centers inside the Hg0.6Mg0.4Te ternary compound.[1]
For RT photodetectors, high resistivity is necessary (threshold value 

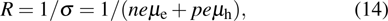 |


The density of the thermal-produced free electron–hole pairs in the unit volume of an intrinsic semiconductor crystal is given by[28]
 |
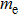


In the present work, the electronic structure and transport properties of the HgxMg1−xTe ternary compound, as a combination of MgTe and HgTe binary compounds, are theoretically studied. This study is based on the simulation of the HMT by the ABINIT package and the results indicate that addition about 60% Hg to MgTe satisfies the requirements of a good RT photodetector. These simulations, including the response function simulation by the MCNP package, introduce Hg0.6Mg0.4Te as an ideal RT photodetector for x and gamma rays spectroscopy, comparable to the Cd0.9Zn0.1Te compound.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] |


















